Symbolic Execution and Program Testing James C King

Symbolic Execution and Program Testing James C. King IBM Thomas J. Watson Research Center 1/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Table of Contents �Introduction �Symbolic Execution �Examples �Symbolic Execution Tree �Examples �An Interactive Symbolic Executor – EFFIGY �Symbolic Execution and Program Testing �Conclusion 2/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Introduction � Testing vs. Formal analysis � Testing �A programmer can be assured that sample test runs work correctly by checking the results � But the correct execution for inputs not in the sample is still in doubt � Formal analysis � Proving the correctness of programs by formal analysis shows great promise � Fundamental problems in reducing theory to practice are not likely to be solved in the immediate future � So let’s take a practical approach between these two extremes – Symbolic Execution ! 3/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution (1/8) � What is symbolic execution ? � Instead of supplying the normal inputs to a program, symbolic execution supplies symbols representing arbitrary values � ex) int f(1, 2) int f(α 1 , α 2) � The execution proceeds as in a normal execution except that values may be symbolic formulae over the input symbols program is symbolically executed for a set of classes of inputs, so each symbolic execution result may be equivalent to a large number of normal test cases �A 4/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

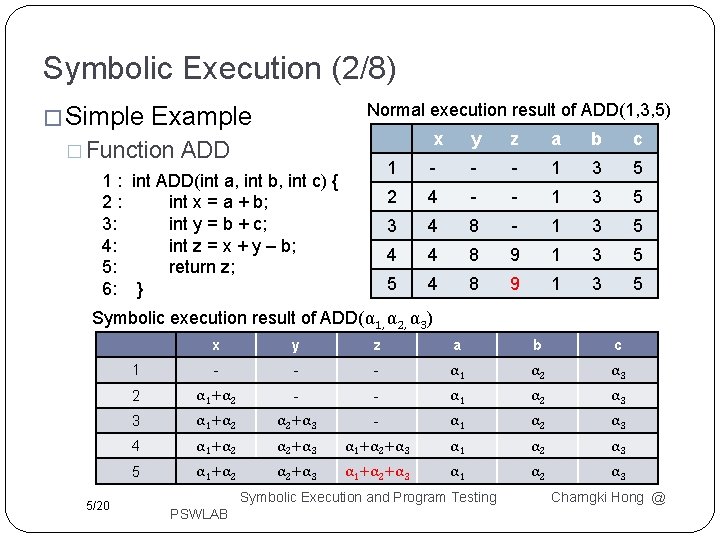
Symbolic Execution (2/8) � Simple Normal execution result of ADD(1, 3, 5) Example � Function ADD 1 : int ADD(int a, int b, int c) { 2: int x = a + b; 3: int y = b + c; 4: int z = x + y – b; 5: return z; 6: } x y z a b c 1 - - - 1 3 5 2 4 - - 1 3 5 3 4 8 - 1 3 5 4 4 8 9 1 3 5 5 4 8 9 1 3 5 Symbolic execution result of ADD(α 1, α 2, α 3) 5/20 x y z a b c 1 - - - α 1 α 2 α 3 2 α 1+α 2 - - α 1 α 2 α 3 3 α 1+α 2 α 2+α 3 - α 1 α 2 α 3 4 α 1+α 2 α 2+α 3 α 1+α 2+α 3 α 1 α 2 α 3 5 α 1+α 2 α 2+α 3 α 1+α 2+α 3 α 1 α 2 α 3 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution (3/8) � Language syntax and the individual programs written in the language need not be changed � The only opportunity to introduce symbolic data is as input to the program � Assignment and Branch statement must be extended to handle symbolic values � Assignment � Right-hand � Branch statement side of the statement may be polynomial statement execution of the IF statement requires path condition(pc) � pc is a boolean expression over the symbolic input � Symbolic 6/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution (4/8) � IF statement (1/2) � The symbolic execution of an IF statement begins in a fashion similar to its normal execution � Since the values of variables are polynomial, the condition is an expression of the form: R ≥ 0, where R is a polynomial � Path Condition � Initial value of pc is true � Using the current path condition(pc), we have two following expressions 7/20 (a) pc q (q is a condition expression) (b) pc ~q Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution (5/8) � IF statement (2/2) � nonforking execution (either of expression is true) � In case that (a) is true, pass control to THEN part In case that (b) is true, pass control to ELSE part � forking execution (neither expressions are true) � Since each alternative is possible in this case, the only complete approach is to explore both control paths � In choosing THEN alternative, the inputs are assumed to satisfy q, this information is recorded in pc by doing assignment pc : = pc ∧ q � Similarly 8/20 choosing the ELSE alternative leads to pc : = pc ∧ ~q Symbolic Execution and Program Testing PSWLAB Charngki Hong @

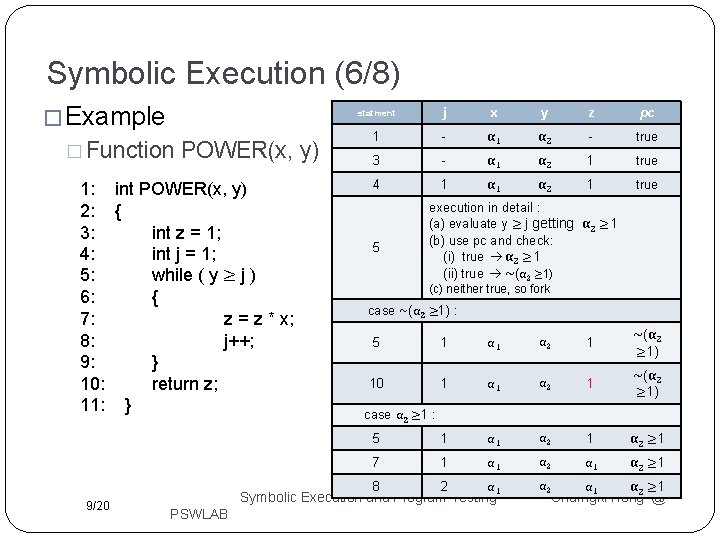
Symbolic Execution (6/8) � Example � Function POWER(x, y) 1: int POWER(x, y) 2: { 3: int z = 1; 4: int j = 1; 5: while ( y ≥ j ) 6: { 7: z = z * x; 8: j++; 9: } 10: return z; 11: } 9/20 statment j x y z pc 1 - α 1 α 2 - true 3 - α 1 α 2 1 true 4 1 α 2 1 true 5 execution in detail : (a) evaluate y ≥ j getting α 2 ≥ 1 (b) use pc and check: (i) true α 2 ≥ 1 (ii) true ~(α 2 ≥ 1) (c) neither true, so fork case ~(α 2 ≥ 1) : 5 1 α 2 1 ~(α 2 ≥ 1) 10 1 α 2 1 ~(α 2 ≥ 1) 5 1 α 2 ≥ 1 7 1 α 2 α 1 α 2 ≥ 1 8 2 α 1 α 2 case α 2 ≥ 1 : Symbolic Execution and Program Testing PSWLAB α 1 α 2 ≥ 1 Charngki Hong @

Symbolic Execution (7/8) � Example � Function POWER(x, y) 1: int POWER(x, y) 2: { 3: int z = 1; 4: int j = 1; 5: while ( y ≥ j ) 6: { 7: z = z * x; 8: j++; 9: } 10: return z; 11: } 10/20 j statment 5 x z pc execution in detail : (a) evaluate y ≥ j getting α 2 ≥ 2 (b) use pc and check: (i) α 2 ≥ 1 α 2 ≥ 2 (ii) α 2 ≥ 1 ~(α 2 ≥ 2) (c) neither true, so fork case ~(α 2 ≥ 2) : 5 2 α 1 α 2 = 1 10 2 α 1 α 2 = 1 5 2 α 1 α 2 ≥ 2 7 2 α 1 α 2 α 1 *α 1 α 2 ≥ 2 8 3 α 1 α 2 α 1 *α 1 α 2 ≥ 2 case α 2 ≥ 2 : Symbolic Execution and Program Testing PSWLAB y Charngki Hong @

Symbolic Execution (8/8) � Commutativity � The result which is computed by normal execution with specific integer inputs is same as executing the program symbolically and then instantiating the symbolic result � ex) � Normal execution ADD(3, 5) = 8 � Symbolic 11/20 execution ADD(α 1, α 2) = α 1 + α 2 Instantiate the symbolic result α 1 = 3, α 2 = 5 3 + 5 = 8 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution Tree (1/3) � We can generate symbolic execution tree characterizing the execution paths followed during the symbolic execution � Associate a node with each statement executed � Associate a directed arc connecting the associated nodes with each transition between statements � For IF statement execution, the associated node has two arcs leaving the node which are labeled “T” and “F” for the true and false part, respectively � Associate the complete current execution state, i. e. variable values, statement counter, and pc with each node 12/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

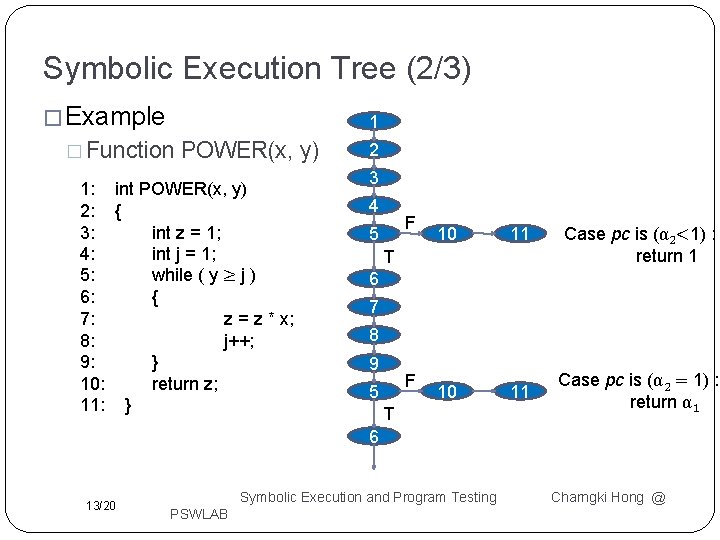
Symbolic Execution Tree (2/3) � Example 1 � Function POWER(x, y) 1: int POWER(x, y) 2: { 3: int z = 1; 4: int j = 1; 5: while ( y ≥ j ) 6: { 7: z = z * x; 8: j++; 9: } 10: return z; 11: } 2 3 4 F 5 10 11 T Case pc is (α 2<1) : return 1 6 7 8 9 F 5 T Case pc is (α 2 = 1) : return α 1 6 13/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

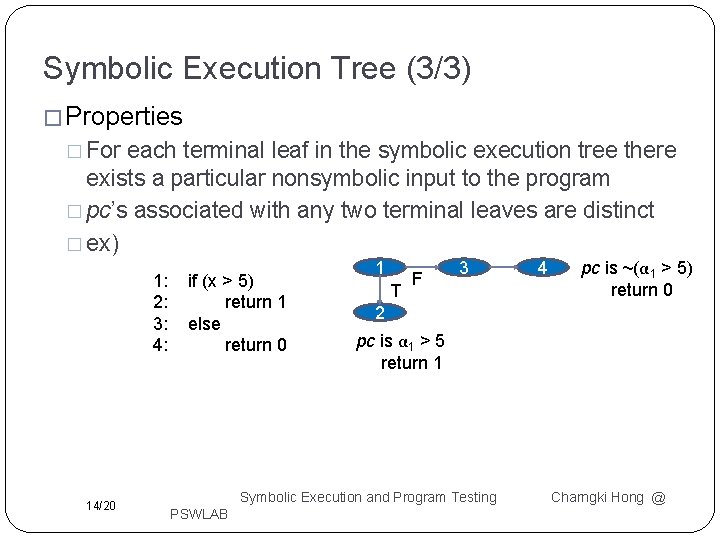
Symbolic Execution Tree (3/3) � Properties � For each terminal leaf in the symbolic execution tree there exists a particular nonsymbolic input to the program � pc’s associated with any two terminal leaves are distinct � ex) 1: 2: 3: 4: 14/20 if (x > 5) return 1 else return 0 1 T F 3 pc is ~(α 1 > 5) return 0 2 pc is α 1 > 5 return 1 Symbolic Execution and Program Testing PSWLAB 4 Charngki Hong @

An Interactive Symbolic Executer – EFFIGY (1/2) � Debugger for symbolic program execution � Basic debugging and testing facilities are provided for symbolic program execution � EFFIGY treats normal execution as a special case � Interactive debugging facilities are available, including: Tracing Breakpoints The user can insert breakpoints before or after any statement State saving 15/20 The user can request to see the statement number, the computational results SAVE, RESTORE Symbolic Execution and Program Testing PSWLAB Charngki Hong @

An Interactive Symbolic Executer – EFFIGY (2/2) � EFFIGY � Testing � Test (2/2) facilities manager Test manager is available for exploring the alternatives presented in the symbolic execution tree � Program Check if the program is running correctly ASSUME(P) pc : = pc ∧ P PROVE(P) 16/20 verifier Check if pc P is true Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution and Program Testing (1/2) � To prove the correctness of a program, the programmer supplies an input predicate and an output predicate with the program � The program is correct if for all inputs which satisfy the input predicate the results produced by the program satisfy the output predicate 17/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Symbolic Execution and Program Testing (2/2) � We can prove the correctness of each path by executing it symbolically as follows: 1. 2. 3. Place ASSUME at the beginning of the path and PROVE at the end of the path Execute the path symbolically If the PROVE at the end of the path displays true, the path is correct, otherwise it is not 18/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Conclusion � Symbolic execution offers the advantage that one symbolic execution may represent a large class of normal executions � EFFIGY system embodies symbolic execution in a general purpose interactive debugging system � Test manager and program verifier are powerful for program testing 19/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @

Discussion 20/20 Symbolic Execution and Program Testing PSWLAB Charngki Hong @