Symbolic Encoding of Neural Networks using Communicating Automata

Symbolic Encoding of Neural Networks using Communicating Automata with Applications to Verification of Neural Network Based Controllers* Li Su, Howard Bowman and Brad Wyble Centre for Cognitive Neuroscience and Cognitive Systems, University of Kent, Canterbury, Kent, CT 2 7 NF, UK {ls 68, hb 5, bw 5}@kent. ac. uk *To Appear in Neural-Symbolic Learning and Reasoning Workshop at Nineteenth International Joint Conference on Artificial Intelligence, EDINBURGH, SCOTLAND, 2005.

Outline • Background: – Symbolic Computation – Sub-symbolic Computation • Motivation for integrating Symbolic and Sub-symbolic Computation – Cognitive Viewpoint – Application Viewpoint • Formal Methods – – Model Checking Specification Properties Result • Summary

Background 1: Symbolic Computation • Traditional symbolic computation: – Systems have explicit elements that correspond to symbols organised in systematic ways, representing information in the external world. – Programmes or rules can manipulate these symbolic representations. – Key characteristic: symbol manipulation.

Background 2: Sub-symbolic Computation • Connectionism/neural networks are computational models inspired by neuron physiology, which can be regarded as sub-symbolic computation: – Aims at massively parallel simple and uniform processing elements, which are interconnected. – Representations are distributed throughout processing elements.

Motivation 1: Cognitive Viewpoint • It has been argued that cognition/mind can be regarded as symbolic computation. (E. g. SOAR, ACT-R and EPIC) • Sub-symbolic (neural network) architectures constitute abstract model of the human brain.

Motivation 1: Cognitive Viewpoint (cont. ) • Combining symbolic and sub-symbolic techniques to specify and justify behaviour of complex cognitive architectures in an abstract and suitable form. – Concurrent, Distributed Control, Hierarchical Decomposition – How do high-level cognitive properties emerge from interactions between low-level neuron components? • Our approach is to encode and reason about cognitive systems or neural networks in symbolic form. – E. g. Formal Methods. – Automatic mathematical analysis can be applied.

Motivation 2: Application Viewpoint • Connectionist networks can be applied to extending traditional controllers in order to handle: – – Catastrophic changes Gradual degradation Complex and highly non-linear systems E. g. aircraft, spacecraft or robots • Reliability/Stability of adaptive systems (neural networks) needs to be guaranteed in safety/mission critical domains. • However, connectionist models rarely provide an indication of the accuracy or reliability of their predictions.

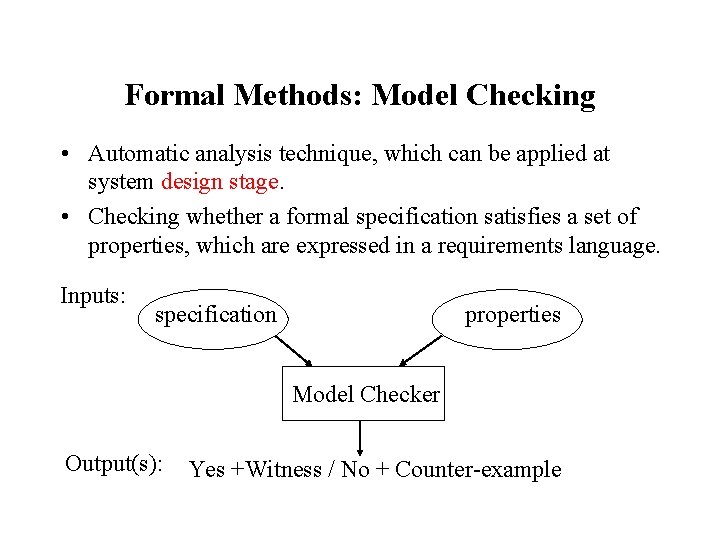
Formal Methods: Model Checking • Automatic analysis technique, which can be applied at system design stage. • Checking whether a formal specification satisfies a set of properties, which are expressed in a requirements language. Inputs: specification properties Model Checker Output(s): Yes +Witness / No + Counter-example

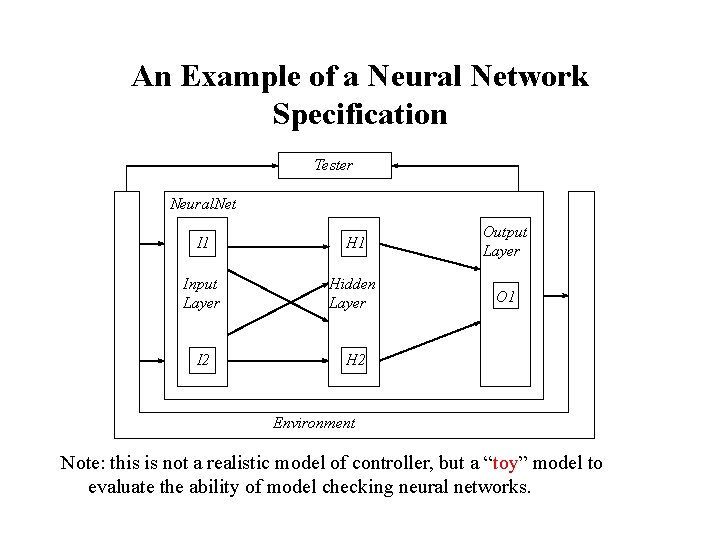
An Example of a Neural Network Specification Tester Neural. Net I 1 H 1 Output Layer Input Layer Hidden Layer O 1 I 2 H 2 Environment Note: this is not a realistic model of controller, but a “toy” model to evaluate the ability of model checking neural networks.

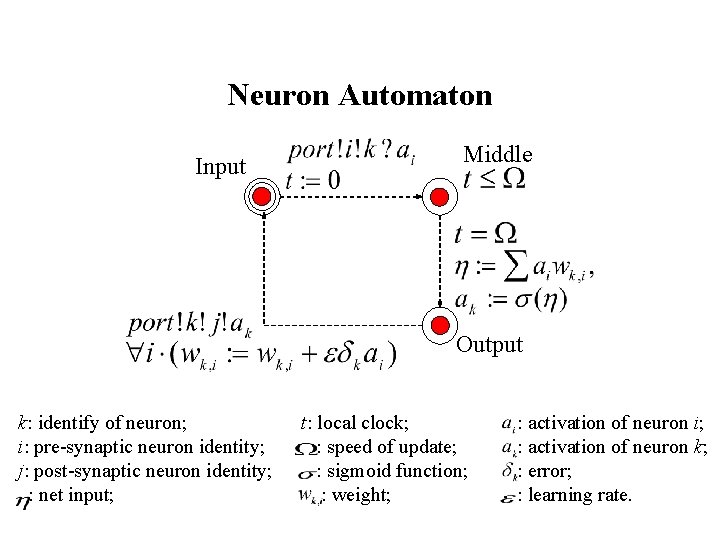
Neuron Automaton Input Middle Output k: identify of neuron; i: pre-synaptic neuron identity; j: post-synaptic neuron identity; : net input; t: local clock; : speed of update; : sigmoid function; : weight; : activation of neuron i; : activation of neuron k; : error; : learning rate.

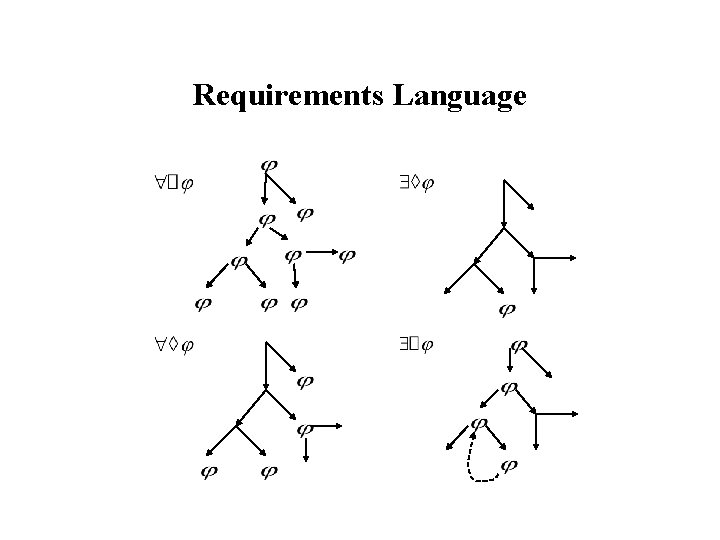
Requirements Language

Requirements Language (cont. ) • Reachability Properties: – E. g. • Safety Properties: – E. g. – • Liveness Properties: – E. g. Note: the state formula success is true when SSE is less than a specified value.

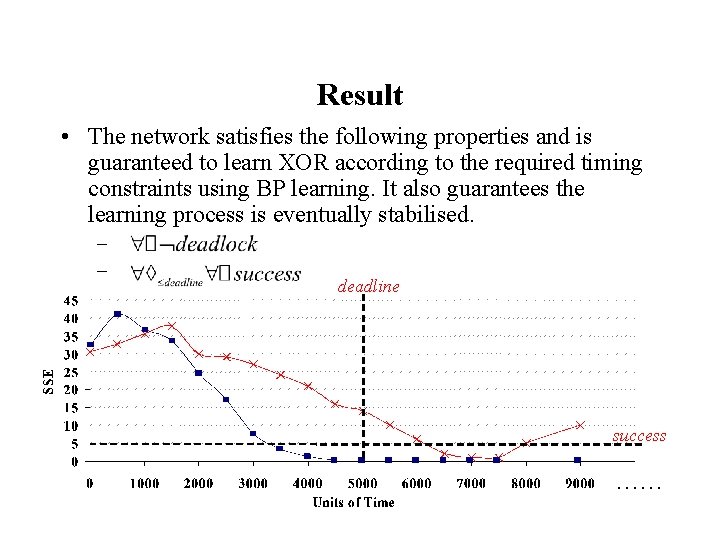
Result • The network satisfies the following properties and is guaranteed to learn XOR according to the required timing constraints using BP learning. It also guarantees the learning process is eventually stabilised. – – deadline success ……

Summary • Formal methods are justifiable techniques to represent lowlevel neural networks. They can also help to understand how high-level cognitive properties emerge from interactions between low-level neuron components. • Formal methods may allow neural networks within engineering applications to be specified and justified at the system design stage. • Verifications may give theoretically well-founded ways to evaluate and justify learning methods. Some pproperties can be hard to justify by simulation. – Simulations can only test that something occurs, but are unable to test that something can never occur without explicit mathematical analysis. (An open issue. )