Symbolic analysis and design of communication systems using

Symbolic analysis and design of communication systems using computer algebra systems Prof. Dr Miroslav Lutovac Dr Dejan Tošić School of Electrical Engineering at the University of Belgrade, Serbia

Overview • • Get back to basic understanding Numeric vs. Symbolic Computation Computer as a symbol processor Schematic as a symbolic object Programs as knowledge repositories A step by step example: QAM Benefits from symbolic techniques

James Kaiser - 50 years of SP Ø It has become so easy to do so much computation using computers that people will press keys on the keyboard without thinking what they are doing Ø It's so easy to generate a tremendous amount of garbage that you've got to understand what it is you're doing Fifty Years of SP (1998), page 54

James Kaiser: “back to basics” ü So it is very important that we get back to basic understanding, get a much better grounding of what science underlies the phenomenon we are looking at ü I mean, this world is not an ideal world ü It's time-varying and nonlinear Fifty Years of SP (1998), page 54

James Kaiser: “understand tools” q Young people or anybody, really who are using these tools have got to thoroughly understand what assumptions underlie the tool that they are using q That will tell them what they can expect to get out Fifty Years of SP (1998), page 54

Numerical ambiguity: 0. 3 - 0. 1 == 0. 2? MATLAB Command Window >> a = 0. 3 -0. 1 a = 0. 2000 >> b = 0. 2000 >> a==b ans = 0 0. 3 – 0. 1 ≠ 0. 2

Why is 0. 3 -0. 1 ≠ 0. 2 ? MATLAB Command Window >> sym(0. 8 -0. 6, 'd') ans =. 2000000006661338147750939 >> sym(0. 2, 'd') ans =. 2000000001110223024625157 >> sym(0. 3 -0. 1, 'd') ans =. 1999999998334665463062265 >> sym(0. 6 -0. 4, 'd') ans =. 1999999995559107901499374

Numeric vs. Symbolic Computation >> (2/10)==(1 -8/10) ans = 0 >> sym(2/10)==sym(1 -8/10) ans = 1 Numeric is false Symbolic is true >> a=1; a=a-0. 2; a=a-0. 2 a = 5. 5511 e-017 a ≈ 0, a ≠ 0

Numeric simulation might fail

Symbolic computation finds exact solution

Algebraic loop • Symbolic analysis of systems is inherently immune to the problem imposed by algebraic loops occurring when two or more blocks with direct feed-through of their inputs form a feedback loop • Numeric simulations of algebraic loops considerably reduce the speed of a simulation and may be unsolvable • Symbolic simulation successfully and accurately computes the required response; it finds the exact solution

Computer as a symbol processor • Computers have become recognized as symbol processors (Oppenheim and Nawab 1992) • Program can be viewed as a set of instructions for manipulating symbols • Numbers are only one of the kinds of symbols that the computer can handle

Schematic as a symbolic object q System model is a symbolic object q It contains all details for drawing, symbolic solving, simulating, and implementing: 1. Analyze the schematic as the symbolic object 2. Identify symbolic system parameters 3. Knowledge embedded in the schematic object can be used to generate implementation code or to derive transfer function

From schematic to system property system = { {"Multiplier", {{6, 0}, {6, 3}}, k 1}, {"Delay", {{4, 5}, {4, 7}}, 1}, {"Adder", {{7, 8}, {8, 5}, {9, 8}, {8, 9}}, {1, 1, 2, 0}}, {"Input", {0, 8}, "X"}, {"Output", {9, 8}, "Y 1 L"}, . . . , {"Line", {{6, 8}, {7, 8}}} } 1. Find transfer function s = H 1*(H 1/. z->1/z) + H 2*(H 2/. z->1/z) //Full. Simplify 2. Simplify expression

Computer as intelligence amplifier • Symbol processor with the appropriate programs is usable on a much wider range of tasks, such as intelligence amplifier or augmenting our ability to think • Programming has become a task of knowledge accumulation telling the computer what to know, when to use, and how to apply the knowledge in solving problems

What to know - How to apply q WHAT TO KNOW: symbolic object that contains a procedure for automated generation of the schematic for an arbitrary number of parts q HOW TO APPLY: draw system, solve symbolically, simulate, and implement system 1. Automatically generate system parameters 2. Automatically generate schematic with symbolic or numeric parameters 3. Solve symbolically: find the transfer function, impulse response, or property of the system from the schematic 4. Automatically generate implementation code 5. Simulate for specified symbolic parameter values

What to know - When to use q q 1. 2. 3. 4. 5. WHAT TO KNOW: symbolic object that contains a procedure for automated generation of the schematic for an arbitrary number of parts WHEN TO USE: When Laplace or z-transform cannot be found When numeric computations fail When symbolic expressions have a large number of parameters When derivation by hand is very time consuming and difficult When symbolic optimization can reduce the number of parameters used in numeric optimization

Knowledge repositories • Programs are viewed as knowledge repositories • Programs should be written to communicate … • … not simply to compute

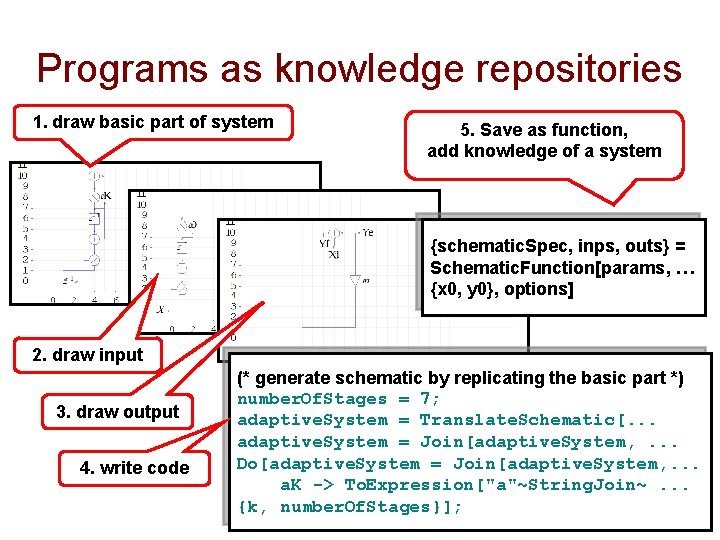
Programs as knowledge repositories 1. draw basic part of system 5. Save as function, add knowledge of a system {schematic. Spec, inps, outs} = Schematic. Function[params, … {x 0, y 0}, options] 2. draw input 3. draw output 4. write code (* generate schematic by replicating the basic part *) number. Of. Stages = 7; adaptive. System = Translate. Schematic[. . . adaptive. System = Join[adaptive. System, . . . Do[adaptive. System = Join[adaptive. System, . . . a. K -> To. Expression["a"~String. Join~. . . {k, number. Of. Stages}];

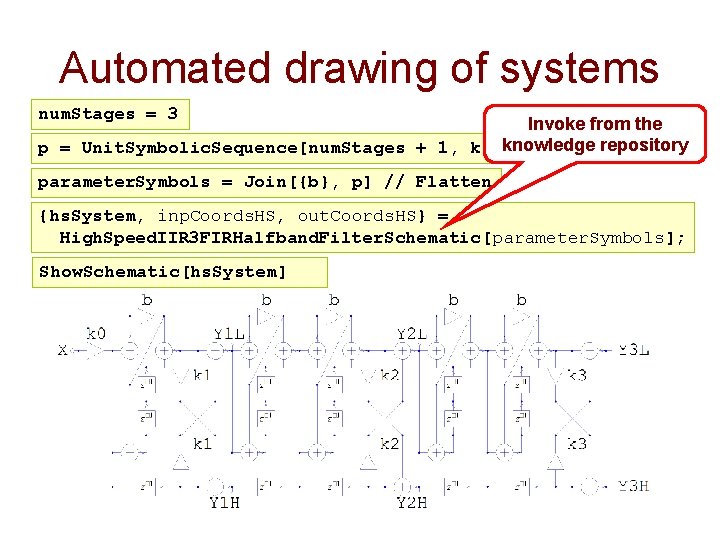
Automated drawing of systems num. Stages = 3 Invoke from the repository p = Unit. Symbolic. Sequence[num. Stages + 1, k, knowledge 0] parameter. Symbols = Join[{b}, p] // Flatten {hs. System, inp. Coords. HS, out. Coords. HS} = High. Speed. IIR 3 FIRHalfband. Filter. Schematic[parameter. Symbols]; Show. Schematic[hs. System]

Programs written to communicate system = { {"Multiplier", {{6, 0}, {6, 3}}, k 1}, {"Delay", {{4, 5}, {4, 7}}, 1}, {"Adder", {{7, 8}, . . . , {1, 1, 2, 0}}, {"Input", {0, 8}, "X"}, . . . , {"Line", {{6, 8}, {7, 8}}}}

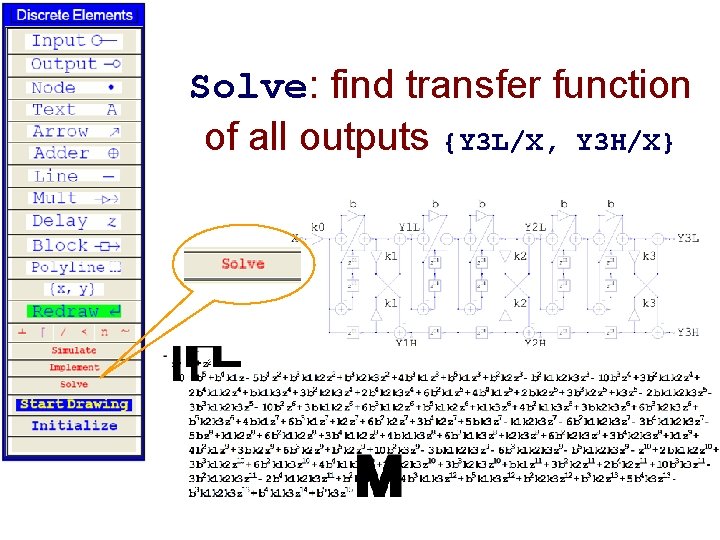
Solve: find transfer function of all outputs {Y 3 L/X, Y 3 H/X}

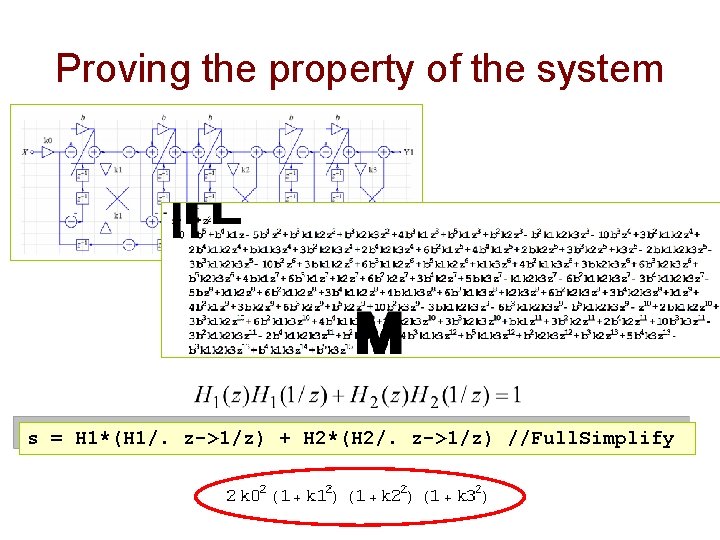
Proving the property of the system s = H 1*(H 1/. z->1/z) + H 2*(H 2/. z->1/z) //Full. Simplify

Deriving new property s = H 1*(H 1/. z->1/z) + H 2*(H 2/. z->1/z) //Full. Simplify Solve[s == 1, k 0] num 3 = Numerator[h 3 L//Together]/. z -> -1 Solve[num 3==0, k 2]

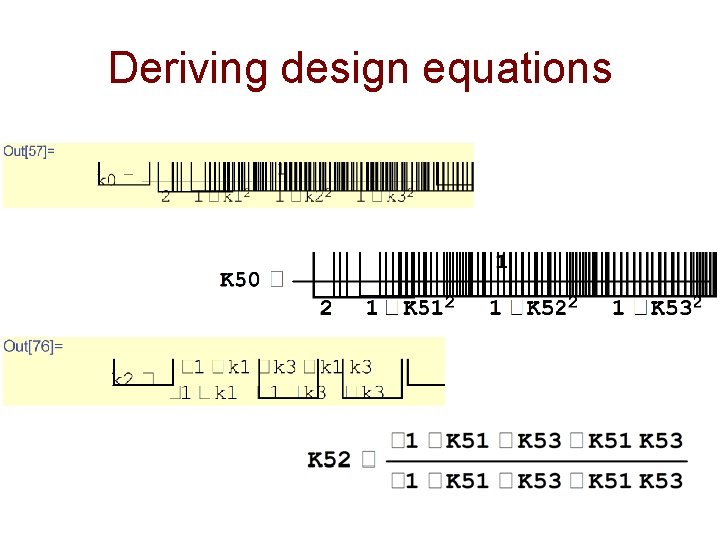
Deriving design equations

Generating implementation code Discrete. System. Implementation[hs. System, "hsf"] {{Y 9 p 8, Y 9 p 0, Y 31 p 0}, {Y 4 p 5, Y 4 p 3, Y 2 p 8}} = 4. Usage 1. Output variables 2. Input variables hsf[{Y 0 p 8}, {Y 4 p 7, Y 4 p 5, Y 28 p 0}, {b, k 0, k 1, k 2, k 3}] is the template for calling the procedure. 3. System parameters The general template is {output. Samples, final. Conditions} = procedure. Name[input. Samples, initial. Conditions, system. Parameters]. See also: Discrete. System. Implementation. Processing

Get information about implementation procedure ? ? implementation. Procedure[data. Samples_List, initial. Conditions_List, system. Parameters_List] : = Module[{Y 0 p 10, Y 4 p 9, Y 4 p 3, a 2, a 3, b 1, b 2, b 3}, {a 2, a 3, b 1, b 2, b 3}=system. Parameters; {Y 0 p 10}=data. Samples; {Y 4 p 9, Y 4 p 3}=initial. Conditions; 4. Code 1. Variables 2. Input variables 3. Initial conditions Y 3 p 0=b 3 Y 0 p 10; Y 3 p 4=b 2 Y 0 p 10; Y 3 p 10=b 1 Y 0 p 10; Y 4 p 5=Y 3 p 4+Y 4 p 3; Y 8 p 10=Y 3 p 10+Y 4 p 9; Y 5 p 0=a 3 Y 8 p 10; Y 5 p 6=a 2 Y 8 p 10; Y 4 p 1=Y 3 p 0 -Y 5 p 0; Y 4 p 7=Y 4 p 5 Y 5 p 6; {{Y 8 p 10}, {Y 4 p 7, Y 4 p 1}}]

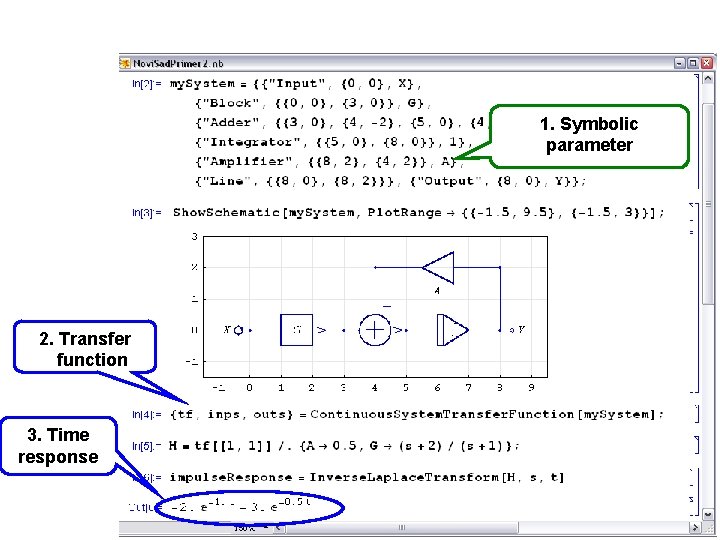
1. Symbolic parameter 2. Transfer function 3. Time response

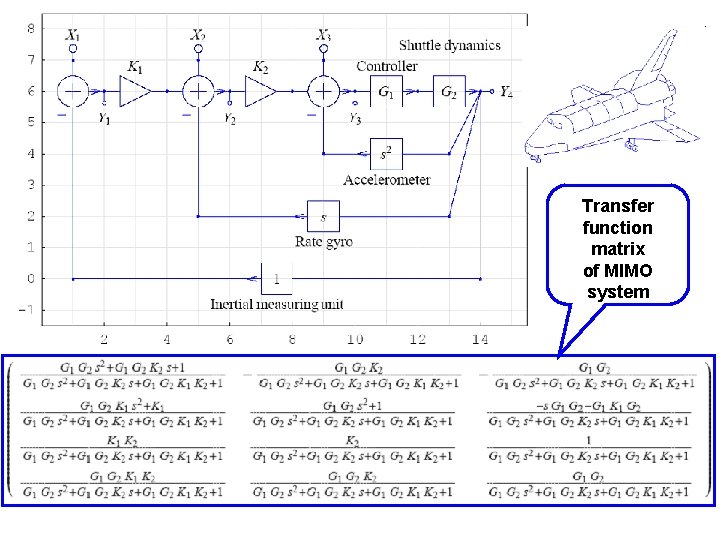
Transfer function matrix of MIMO system

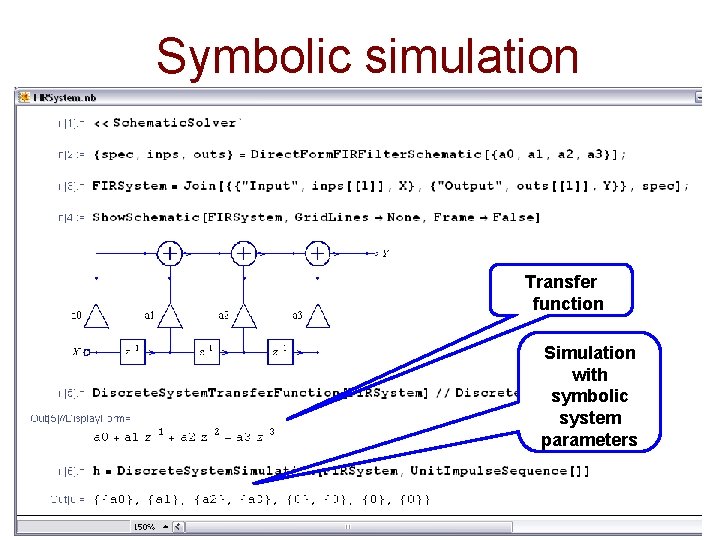
Symbolic simulation Transfer function Simulation with symbolic system parameters

Symbolic processing number. In. Samples = 20; input. Sequence = Unit. Impulse. Sequence[number. In. Samples]; eqns = Discrete. System. Implementation. Equations[hs. System]; initial. Conditions = 0*eqns[[2]] system. Parameters = eqns[[3]] {output. Seq, final. Cond}=Discrete. System. Implementation. Processing[ input. Sequence, initial. Conditions, system. Parameters, hsf]; Each element of the output sequence is a symbolic expression

Response in time domain p={b→ 9/16, k 0→ 0. 24000685, k 1→ 2. 37428, k 2→-0. 54068, k 3→ 0. 1093268} y=Inverse. ZTransform[hs. System /. p, z, n] Use z-transform (if it exists)

How to synthesize a discrete system? 1. For known transfer function Invoke from the knowledge repository H(z) = ( 1 + 2 z -1 + z -2 ) / ( 1 + ½ z -2 ) create schematic of the system {schematic, {inp. Coord}, {out. Coord}} = Transposed. Direct. Form 2 IIRFilter. Schematic[{{1, 2, 1}, {0, 1/2}}]; 2. Add input element and output element system = Join[schematic, {{"Input", inp. Coord, X}, {"Output", out. Coord, Y}}] 3. Draw the block-diagram Show. Schematic[system]

Discrete systems analysis: Find response from the schematic 4. Compute transfer function from the schematic {tf. Matrix, system. Inp, system. Out} = Discrete. System. Transfer. Function[system]; tf = tf. Matrix[[1, 1]]; 5. Input signal represented by a formula sine. Signal = Sin[n/5]; 6. Find output signal sine. Transform = ZTransform[sine. Signal, n, z]; response = Inverse. ZTransform[sine. Transform*tf, z, n]

Discrete systems analysis using symbolic processing 1. Generate a code that implements the system 2. Compute input sequence whose elements can be symbols, numbers, or formulas Discrete. System. Implementation[system, "imp"]; in. Seq = Unit. Sine. Sequence[8, 1/(10 π), 0]; 3. Process the input sequence with the code {out. Seq, finals} = Discrete. System. Implementation. Processing[in. Seq, {0, 0}, {}, imp]; The seventh element of the output sequence is not a number; it is an expression

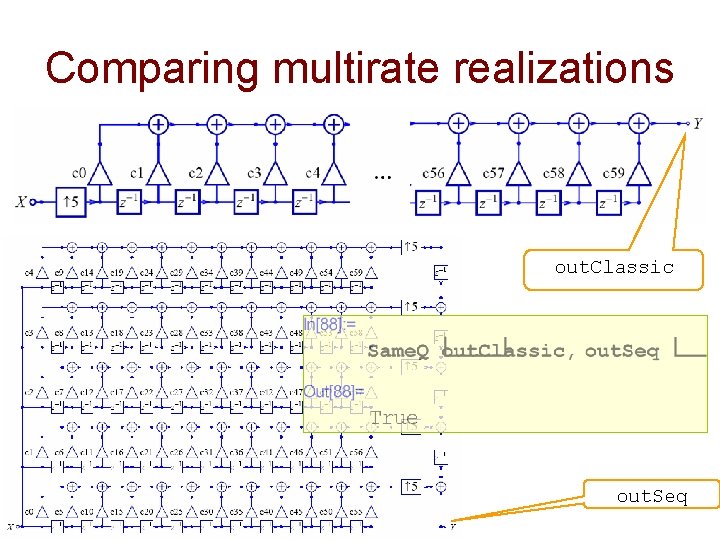
Comparing multirate realizations out. Classic out. Seq

Quadrature Amplitude Modulation A step by step example

What is QAM? • Quadrature Amplitude Modulation (QAM) is a widely used method for transmitting digital data over bandpass channels • The simulation of a simplified and idealized QAM system follows

Read-in the knowledge

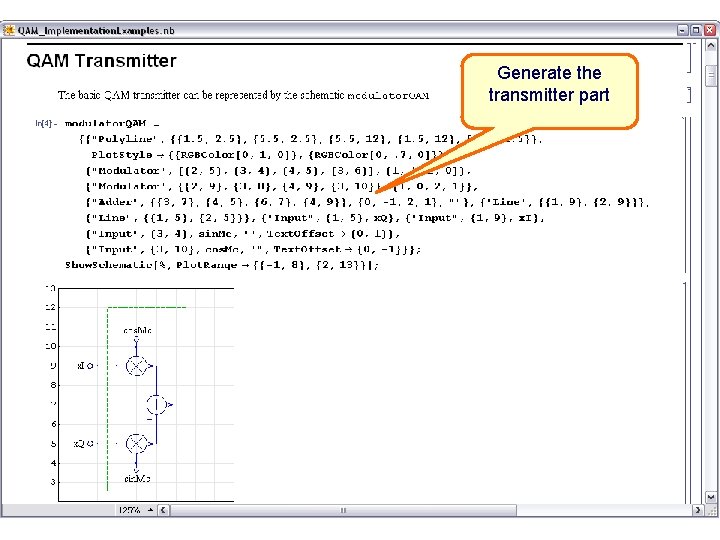
Generate the transmitter part

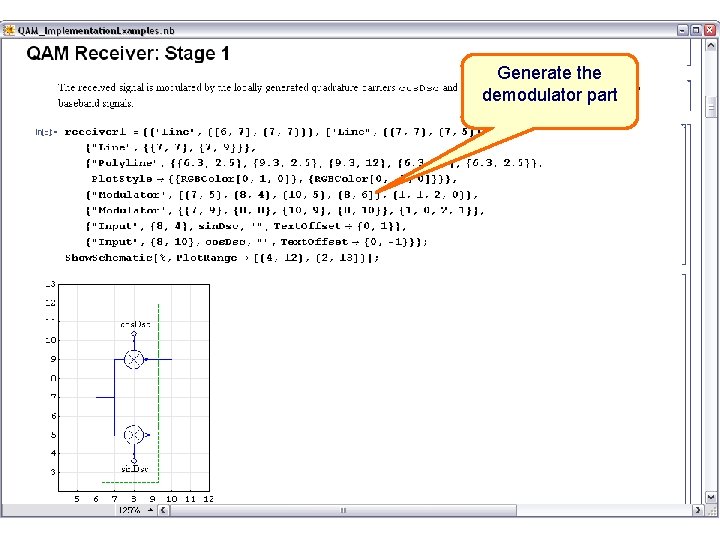
Generate the demodulator part

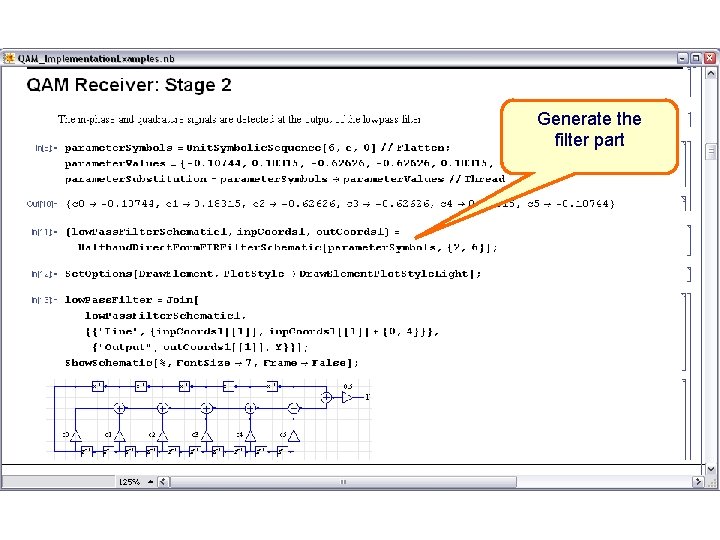
Generate the filter part

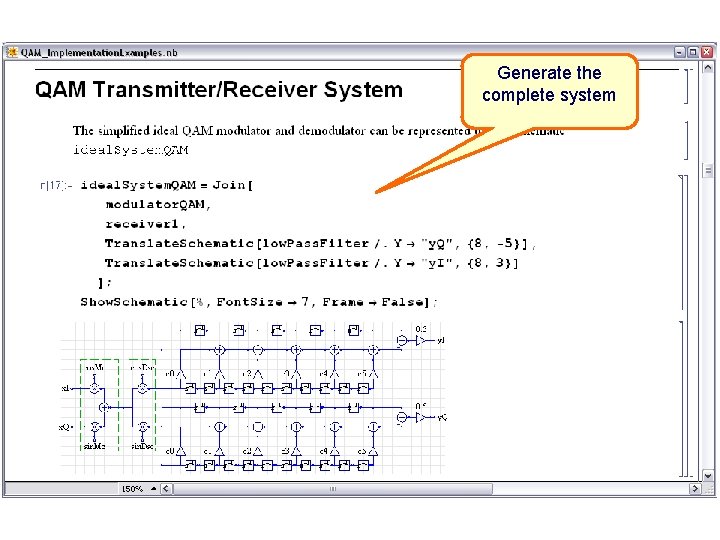
Generate the complete system

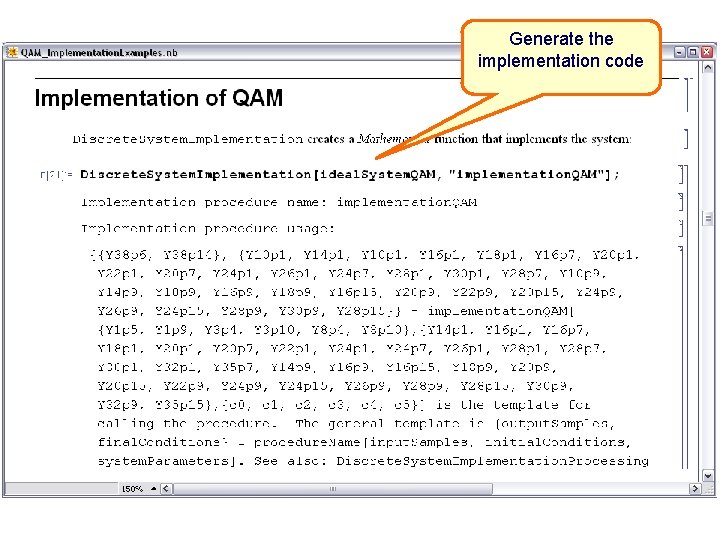
Generate the implementation code

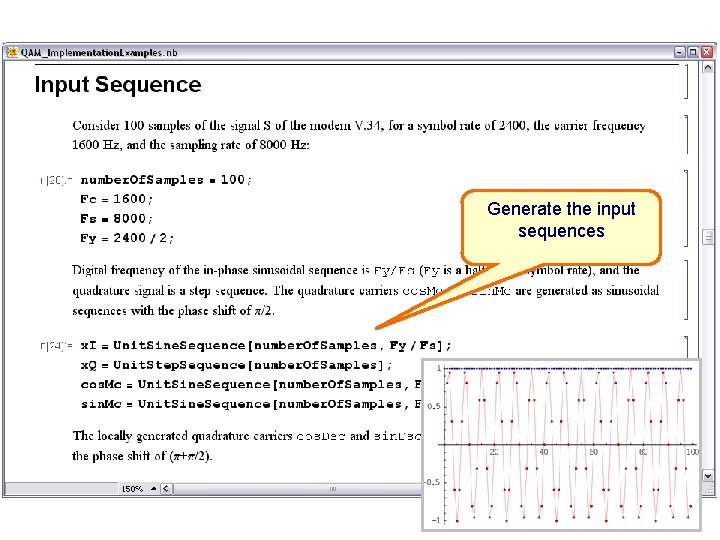
Generate the input sequences

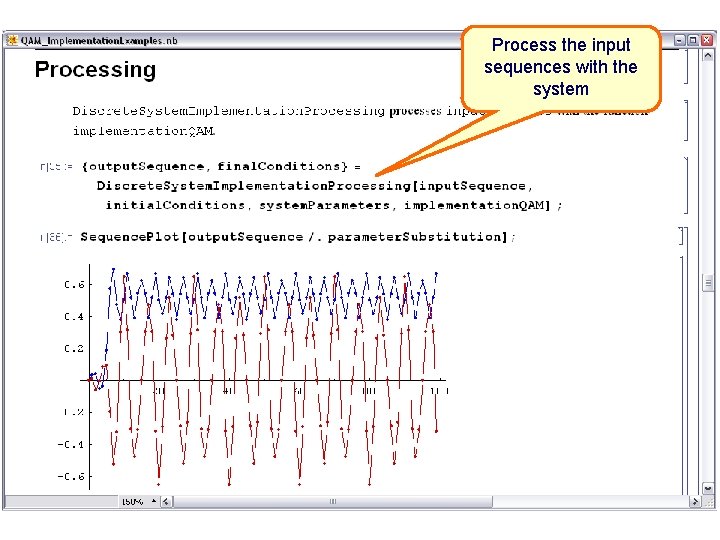
Process the input sequences with the system

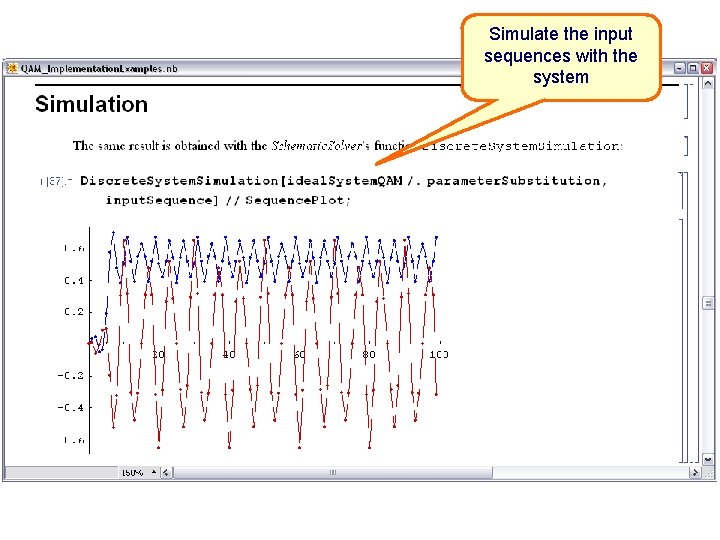
Simulate the input sequences with the system

Miscellaneous examples

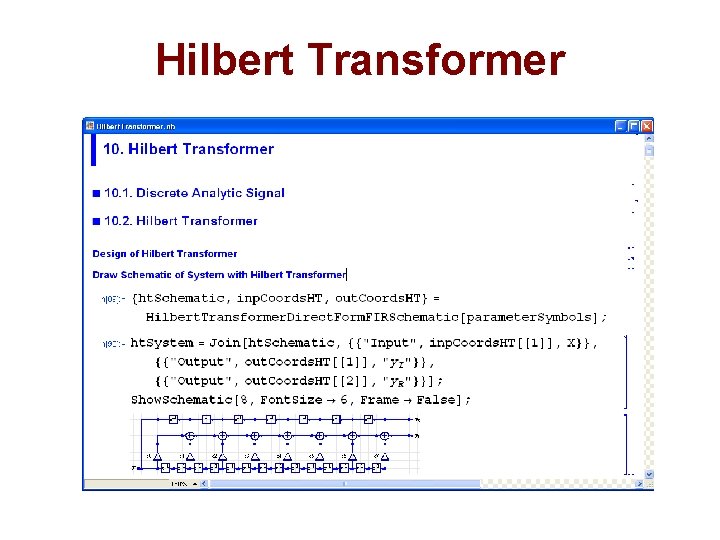
Hilbert Transformer

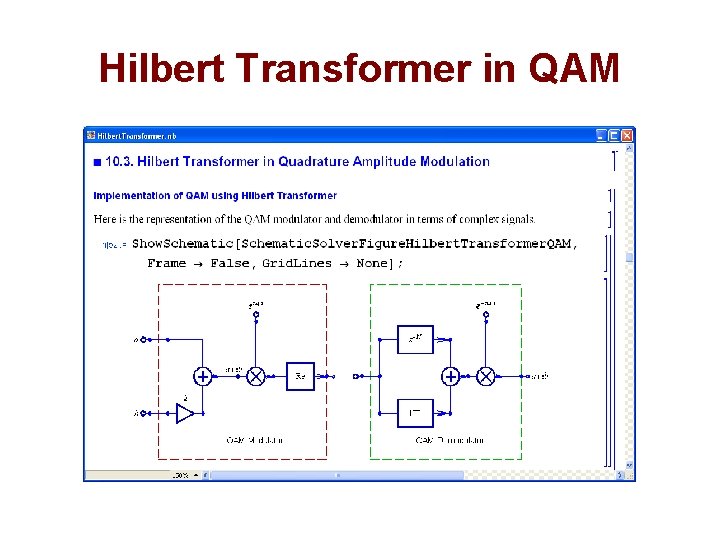
Hilbert Transformer in QAM

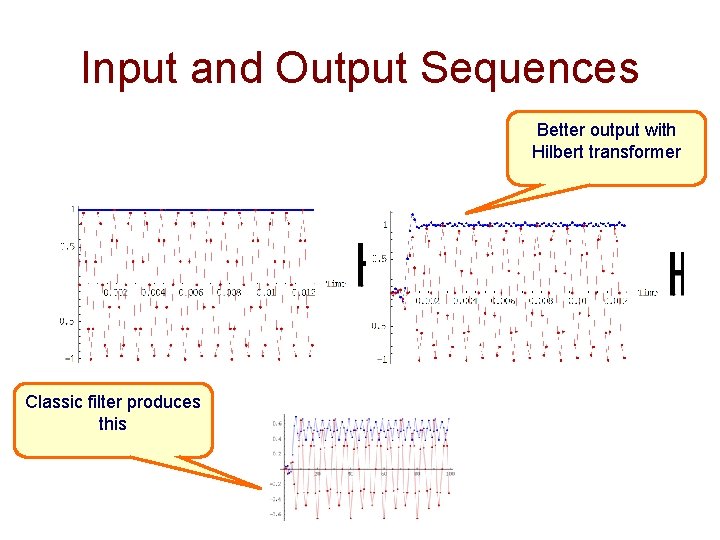
Input and Output Sequences Better output with Hilbert transformer Classic filter produces this

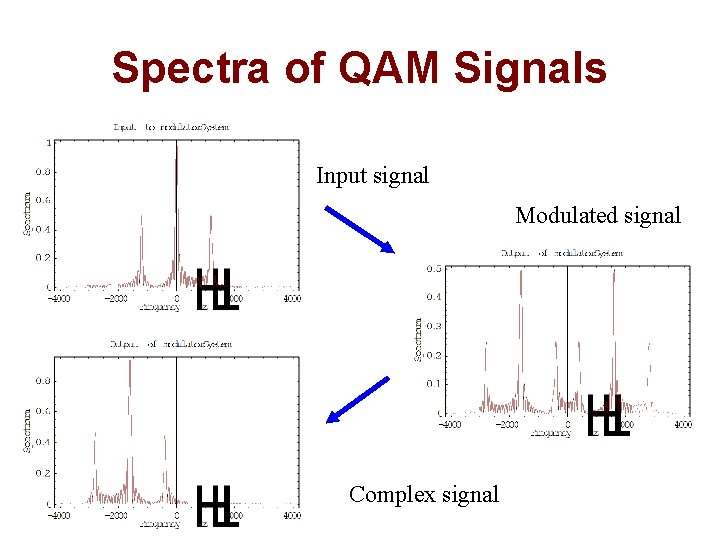
Spectra of QAM Signals Input signal Modulated signal Complex signal

Amplitude Modulation

Nonlinear systems Can we find the output signal as a closed-form expression in terms of the sample index?

Nonlinear systems: Symbolic response 1. 2. Draw the schematic Automatically generate a code that implements the system 3. Compute the successive output values 4. Eliminate the initial states and find the relation between the output samples Discrete. System. Implementation[system, "implement"]; {{y 2}, {d 2}} = implement[{1, 10}, {d 1}, {}]; {{y 3}, {d 3}} = implement[{1, 10}, {d 2}, {}]; eqns = Reduce[{y[n-1]==y 2, y[n]==y 3}, {d 1}]; 5. Find the recurrence equation 6. Load knowledge for solving recurrence equations 7. Find a closed-form solution RSolve[{reduced. Eqn, y[0]==0}, y[n], n]; reduced. Eqn =(15 y[-1 + n] == -10 + 16 y[n]); <<Discrete. Math`RSolve`

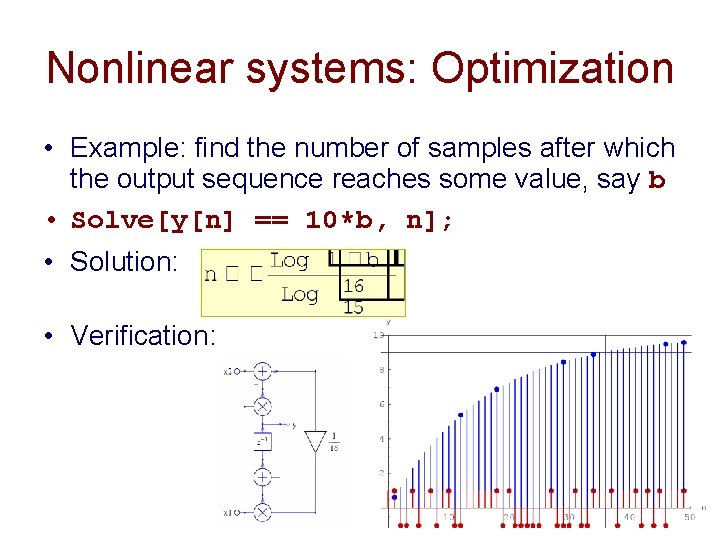
Nonlinear systems: Optimization • Example: find the number of samples after which the output sequence reaches some value, say b • Solve[y[n] == 10*b, n]; • Solution: • Verification:

Adaptive System

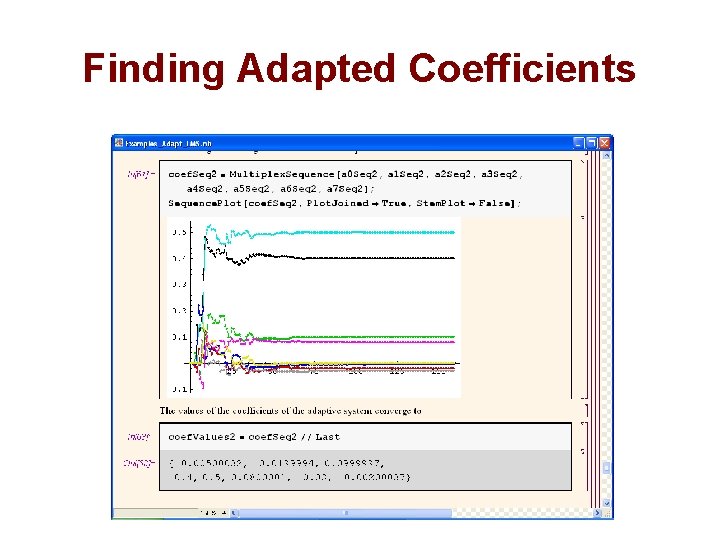
Finding Adapted Coefficients

Symbolic Response of the Unknown System • desired. Signal. Symbolic = Discrete. System. Simulation[unknown. System, input. Signal] • {{-0. 0026 b 0}, {-0. 1111 b 0 - 0. 0026 b 1}, {0. 0751 b 0 - 0. 1111 b 1 - 0. 0026 b 2}, {0. 05 b 0 + 0. 0751 b 1 - 0. 1111 b 2 - 0. 0026 b 3}, {-0. 0517 b 0 + 0. 05 b 1 + 0. 0751 b 2 - 0. 1111 b 3 - 0. 0026 b 4}, … }= {{0. 000013}, {0. 0006075}, {0. 0015865}, {-0. 013902}, . . . }

Automatic Gain Control Nonlinear Power

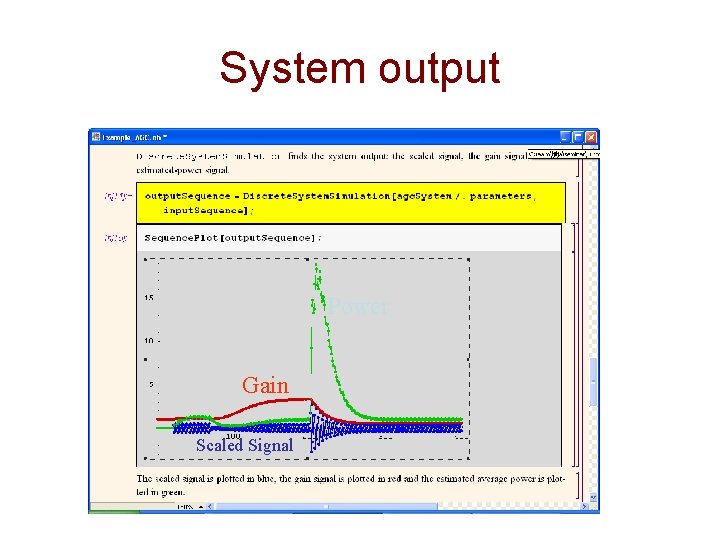
System output Power Gain Scaled Signal

Algorithm development Efficient method for approximating the reciprocal using a modified Newton-Raphson iteration

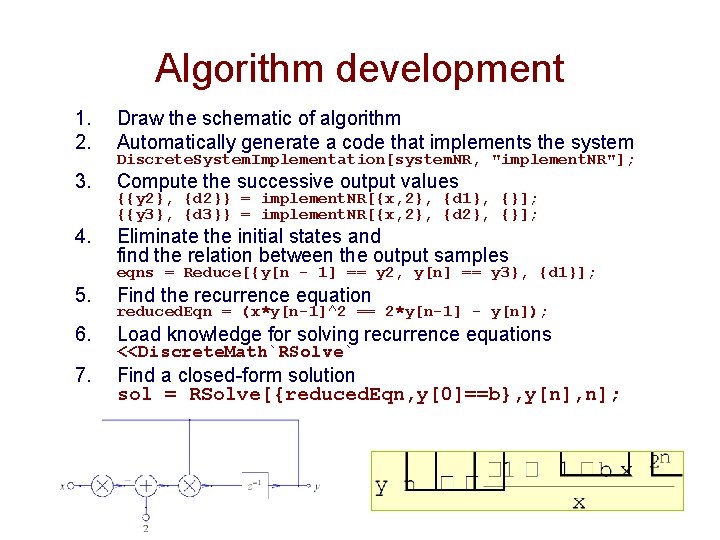
Algorithm development 1. 2. Draw the schematic of algorithm Automatically generate a code that implements the system 3. Compute the successive output values 4. Eliminate the initial states and find the relation between the output samples Discrete. System. Implementation[system. NR, "implement. NR"]; {{y 2}, {d 2}} = implement. NR[{x, 2}, {d 1}, {}]; {{y 3}, {d 3}} = implement. NR[{x, 2}, {d 2}, {}]; eqns = Reduce[{y[n - 1] == y 2, y[n] == y 3}, {d 1}]; 5. Find the recurrence equation 6. Load knowledge for solving recurrence equations 7. Find a closed-form solution sol = RSolve[{reduced. Eqn, y[0]==b}, y[n], n]; reduced. Eqn = (x*y[n-1]^2 == 2*y[n-1] - y[n]); <<Discrete. Math`RSolve`

Algorithm development: Optimization of initial guess • Example: algorithm for implementation of an efficient method for approximating the reciprocal using a modified Newton-Raphson iteration • Find the initial guess to minimize the error of the approximate reciprocal in terms of the given number x, the initial guess b and the number of iterations n: Find. Root[e[n] + 1/2^16 == 0, {b, 2}]; • Solution: b = 1. 98923 • The error is smaller than 2 -16 for x over the range 0. 01 < x < 1

Conclusion • Contemporary trends to use very sophisticated algorithms combine expertise in many areas, such as communications engineering, computer science, ICT, and signal processing • Current symbolic computation environments are powerful in doing symbolic and mixed symbolic-numeric mathematics for technical computing

Conclusion (2) • Programs provide knowledge about design and employ the knowledge in symbolic manipulation: a) automated generation of schematic objects and the corresponding implementation codes b) derivation of the transfer function, system properties and time response c) symbolic optimization

Conclusion (3) • Superiority of symbolic computation against numerical computation was shown by a) the example system with an algebraic loop; CAS yielded the exact solution while the traditional numeric approach failed b) the closed-form solution of a nonlinear LMS subsystem c) deriving the analytic expression for the error of the Newton-Raphson iteration

Conclusion (4) • Benefits of symbolic methods were highlighted from the viewpoint of a) Academia (derivation of time and frequency response, proving system properties) b) Industry (QAM, Hilbert transformer, LMS algorithm, verification of realizations, design alternatives in multirate systems)

Examples and documentation http: //library. wolfram. com/infocenter/Tech. Notes/4814/ http: //www. schematicsolver. com

Further reading 2002 2004 2001 2004 2002