Switching Fabric An Engineering Approach to Computer Networking

Switching - Fabric An Engineering Approach to Computer Networking April 3, 2000 1

Switching Number of connections: from few (4 or 8) to huge (100 K) April 3, 2000 Communication Networks 2

Switching - Basic Assumptions n continuous streams n telephone connections u u no bursts no buffers n connections change n multicast n Blocking u u April 3, 2000 external internal F re-arrangeable F strict sense non-blocking F wide sense non-blocking Communication Networks 3

Multiplexors and demultiplexors n Multiplexor: aggregates sessions n N input lines u Output runs N times as fast as input Demultiplexor: distributes sessions u u n one input line and N outputs that run N times slower Can cascade multiplexors April 3, 2000 Communication Networks 4

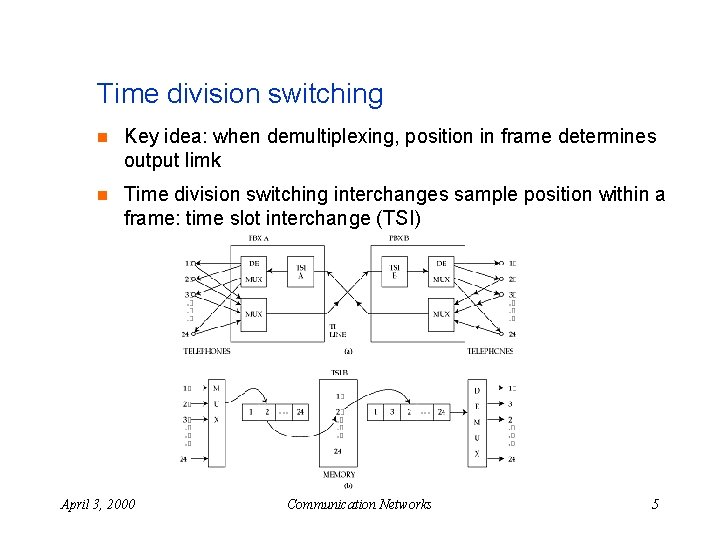
Time division switching n Key idea: when demultiplexing, position in frame determines output limk n Time division switching interchanges sample position within a frame: time slot interchange (TSI) April 3, 2000 Communication Networks 5

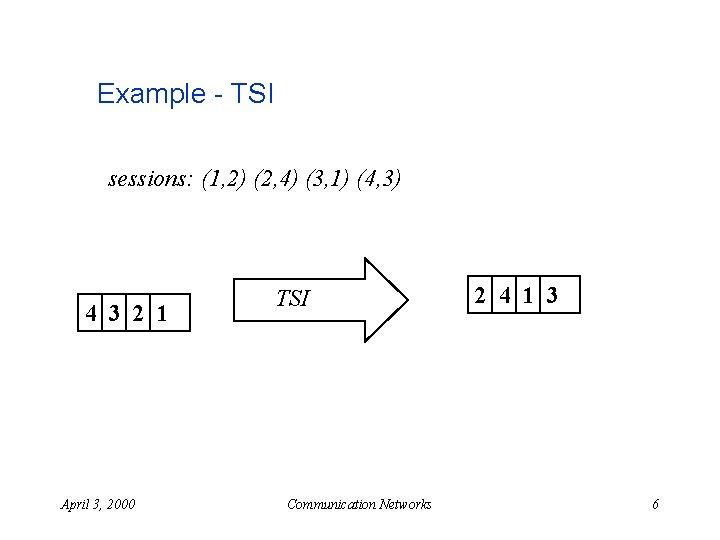
Example - TSI sessions: (1, 2) (2, 4) (3, 1) (4, 3) 4 3 2 1 April 3, 2000 TSI Communication Networks 2 4 1 3 6

TSI n Simple to build. n Multicast n Limit is the time taken to read and write to memory n For 120, 000 circuits u u n need to read and write memory once every 125 microseconds each operation takes around 0. 5 ns => impossible with current technology Need to look to other techniques April 3, 2000 Communication Networks 7

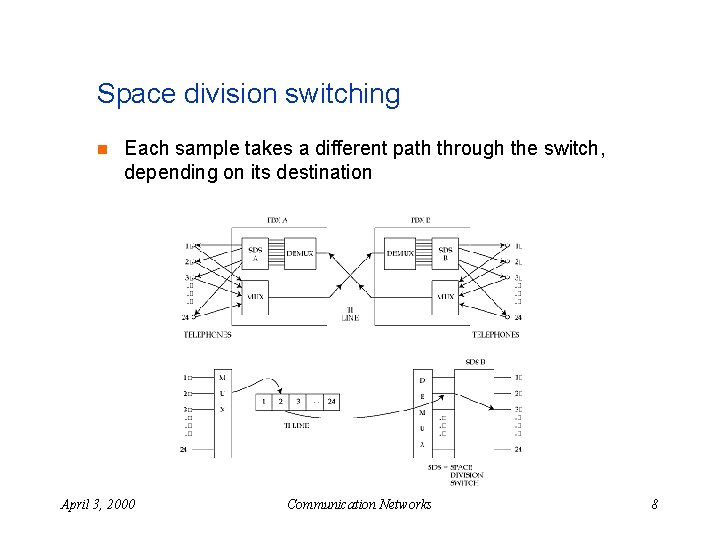
Space division switching n Each sample takes a different path through the switch, depending on its destination April 3, 2000 Communication Networks 8

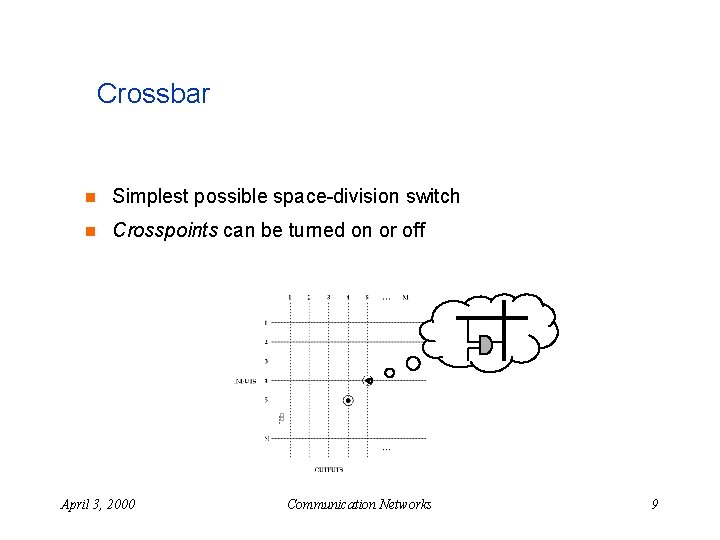
Crossbar n Simplest possible space-division switch n Crosspoints can be turned on or off April 3, 2000 Communication Networks 9

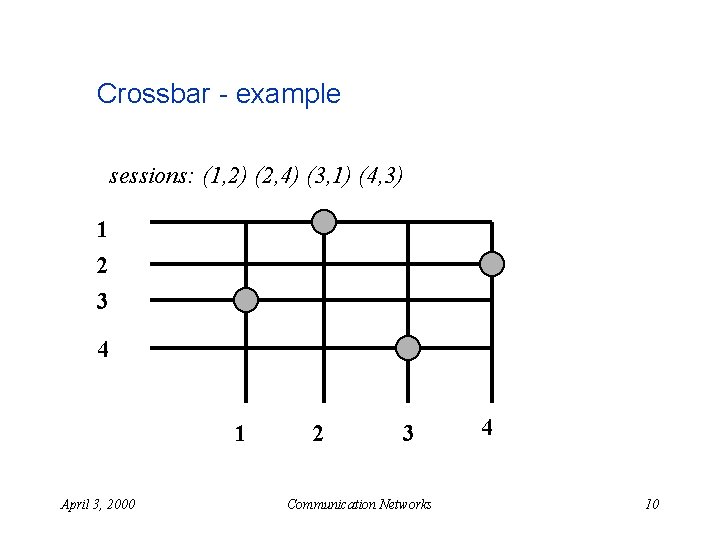
Crossbar - example sessions: (1, 2) (2, 4) (3, 1) (4, 3) 1 2 3 4 1 April 3, 2000 2 3 Communication Networks 4 10

Crossbar n Advantages: u u u n simple to implement simple control strict sense non-blocking Drawbacks u u u April 3, 2000 number of crosspoints, N 2 large VLSI space vulnerable to single faults Communication Networks 11

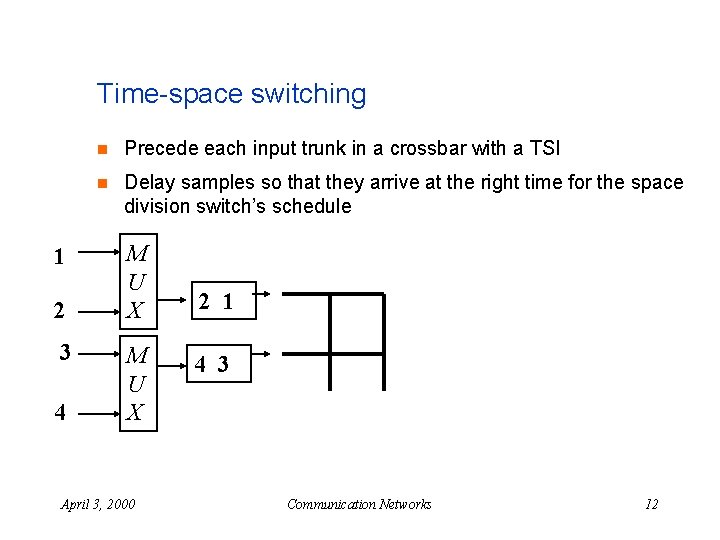
Time-space switching 1 2 3 4 n Precede each input trunk in a crossbar with a TSI n Delay samples so that they arrive at the right time for the space division switch’s schedule M U X April 3, 2000 2 1 4 3 Communication Networks 12

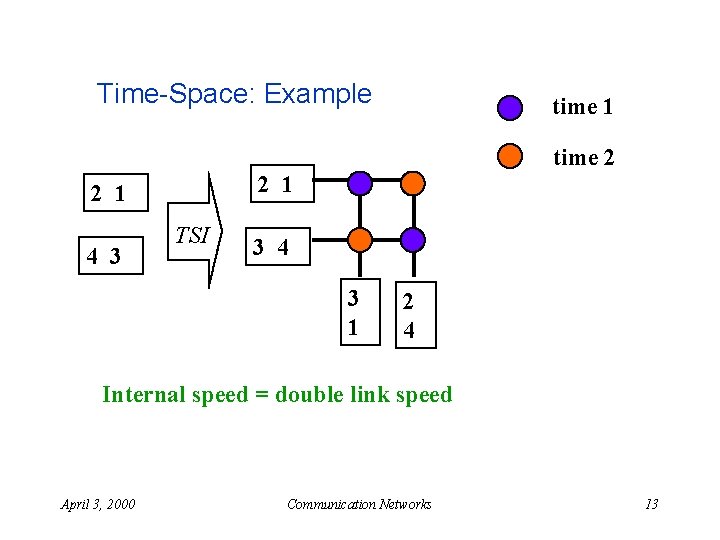
Time-Space: Example time 1 time 2 2 1 4 3 TSI 3 4 3 1 2 4 Internal speed = double link speed April 3, 2000 Communication Networks 13

Finding the schedule n Build a graph u u nodes - input links session connects an input and output nodes. n Feasible schedule n Computing a schedule u April 3, 2000 compute perfect matching. Communication Networks 14

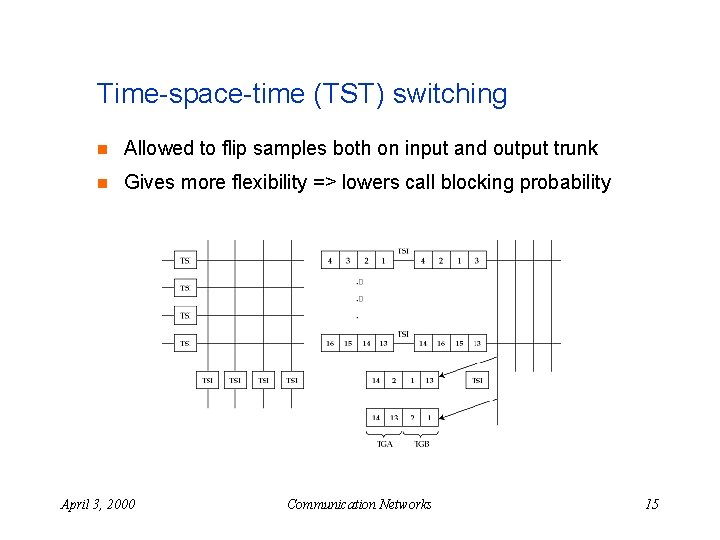
Time-space-time (TST) switching n Allowed to flip samples both on input and output trunk n Gives more flexibility => lowers call blocking probability April 3, 2000 Communication Networks 15

Circuit switching - Space division n graph representation u u u n Feasible schedule u n transmitter nodes receiver nodes internal nodes edge disjoint paths. cost function u u April 3, 2000 number of crosspoints internal nodes Communication Networks 16

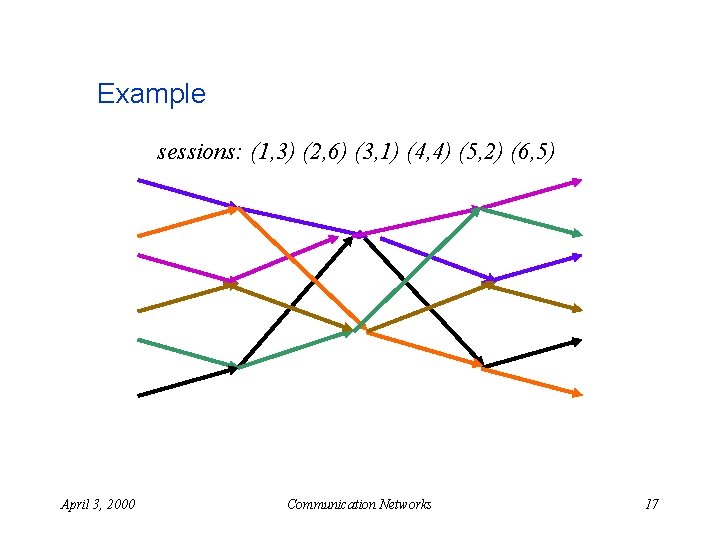
Example sessions: (1, 3) (2, 6) (3, 1) (4, 4) (5, 2) (6, 5) April 3, 2000 Communication Networks 17

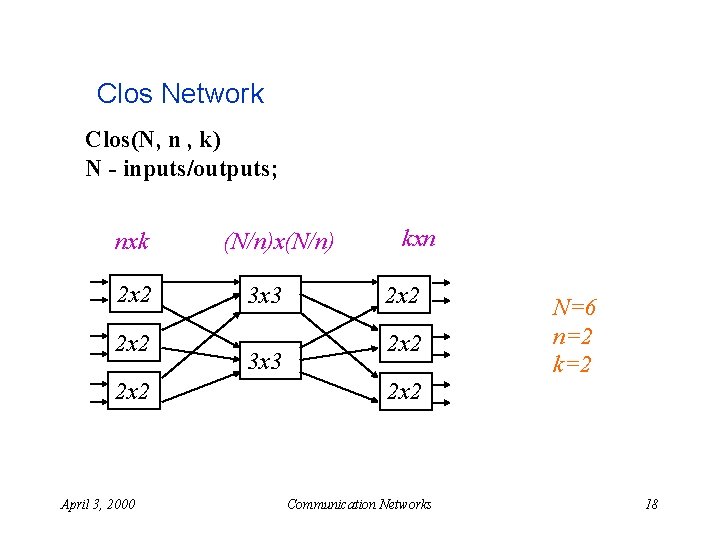
Clos Network Clos(N, n , k) N - inputs/outputs; nxk 2 x 2 April 3, 2000 (N/n)x(N/n) 3 x 3 kxn 2 x 2 N=6 n=2 k=2 2 x 2 Communication Networks 18

Clos Network - strict sense non-blocking n Holds for k >= 2 n-1 n Proof: u u April 3, 2000 Consider and idle input and output Input box connected to at most n-1 middle layer switches output box connected to at most n-1 middle layer switches There exists a "free" middle switch. Communication Networks 19

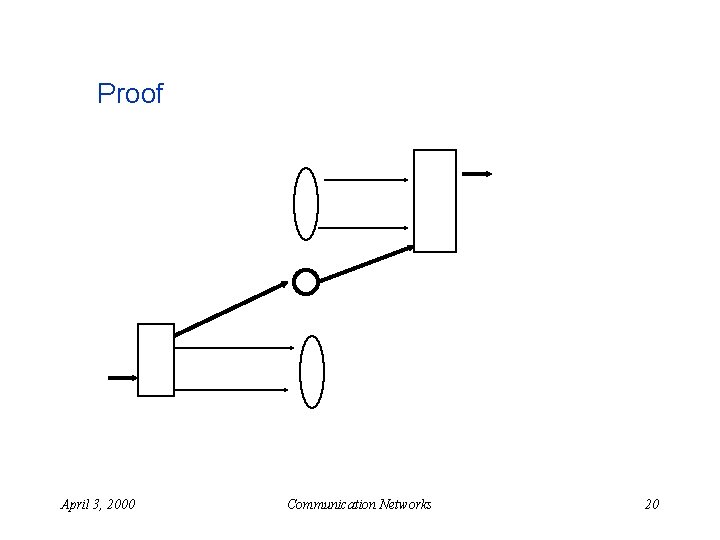
Proof April 3, 2000 Communication Networks 20

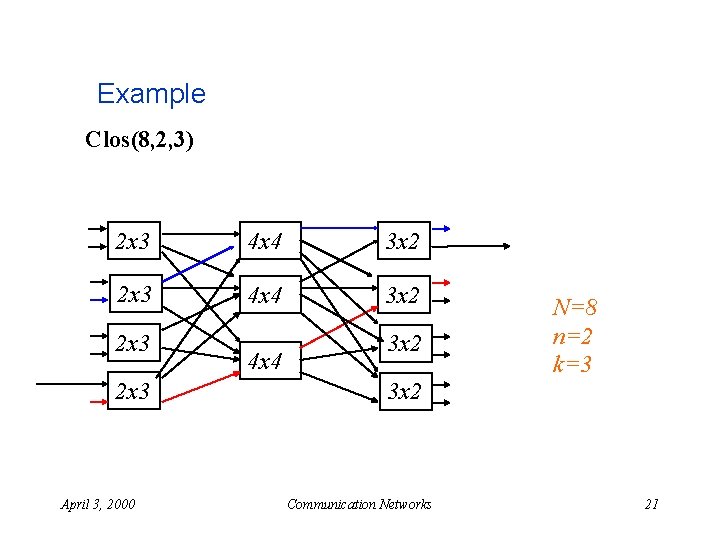
Example Clos(8, 2, 3) 2 x 3 4 x 4 3 x 2 2 x 3 April 3, 2000 4 x 4 3 x 2 N=8 n=2 k=3 3 x 2 Communication Networks 21

Clos Network - rearrangable n Holds for k >= n n Proof: u u n summary: u u n Consider all input and output find a perfect matching. route the perfect matching remaining network is Clos(N-n, n-1, k-1) smaller circuit weaker guarantee Mulicast ? April 3, 2000 Communication Networks 22

Rearrangable Clos Network – routing algorithm n Start at some arbitrary 2 x 2 input switch, and route it to its destination through the upper switch. n Route the other output port of the 2 x 2 switch you reached to its input port through the lower switch. n If the other port in the input switched you reached has not been routed yet, route it through the upper middle switch. n Otherwise, select an arbitrary input port switch that was not yet used, and repeat the procedure. April 3, 2000 Communication Networks 23

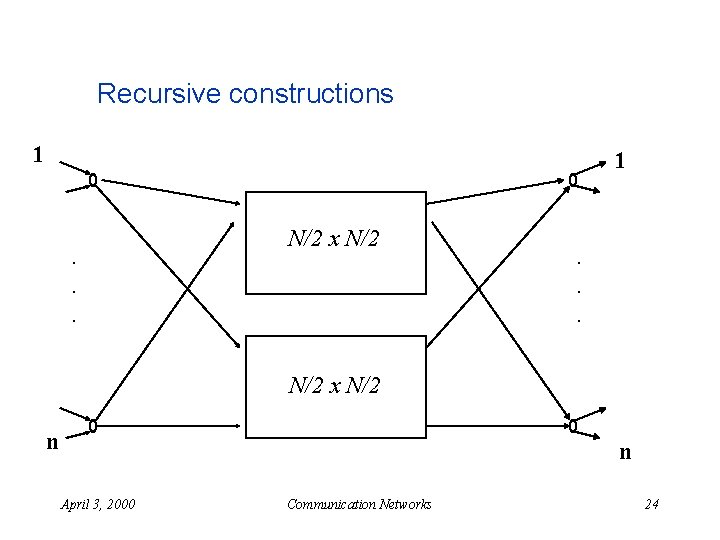
Recursive constructions 1 1 . . . N/2 x N/2 n n April 3, 2000 Communication Networks 24

Algorithm Complexity n N routing steps for each level n Log n levels to do n ===> n Given parallel hardware: O(N) time April 3, 2000 N log n Communication Networks 25

Alternative View of the problem n A graph coloring problem: n Input/output switches = nodes n A match = link n Middle stage switches = colors n This is the well known “Coloring of bi-partite graph” problem. n Heuristics fail miserably!!! April 3, 2000 Communication Networks 26

Another algorithm – matrix based n Specification matrix: u u u n We need an algorithms that will fill up the matrix with a feasible routing: u n Rows = input switches (n) Columns = middle switches (N/n = r) Content = output switches (1. . n) Same number cannot appear in the same column Works also for CLOS with redundancy April 3, 2000 Communication Networks 27

Algorithm Principle n For j=0, 1, 2, … u n Challenges: u u n balance the destination j among the columns efficiency termination We describe an Algorithm by Lee, Hwang, and Carpinelli, T. COM. 44 (11), Nov 1996 April 3, 2000 Communication Networks 28

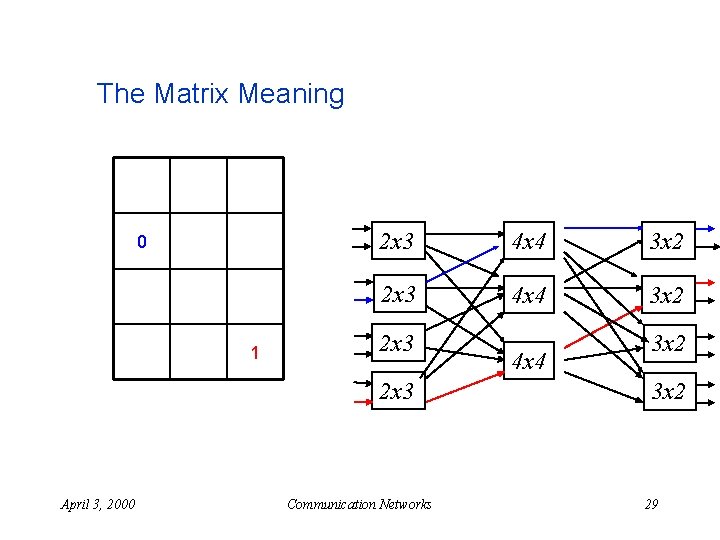
The Matrix Meaning 0 1 2 x 3 4 x 4 3 x 2 2 x 3 April 3, 2000 Communication Networks 4 x 4 3 x 2 29

Data Structures n (j, e), j=0, 1, …n-1, e=0, 1, …, r-1 : - the set of rows {i} such that sij=e n 0(e), e=0, 1, r-1 : - the set of columns {j} such that Si does not contain e n 2(e), e=0, 1, r-1 : - the set of columns {j} such that Si contains e at least twice April 3, 2000 Communication Networks 30

Algorithm 4. (Next Simple Swap) If e> sik i’ 2 nd element of sik repeat step 3 on i’ Init: e=0 1. If 2(e) empty e e+1 if e=r stop; else goto 1 2. if e> si’k goto step 5 5. (Successive Swap) if 2(e) j 1 st element of 2(e) k 1 st element of 0(e) 3. A. B. (simple swap) i 1 st element of (j, e) if e< sik swap sij with sik e’ sik remove i from (j, e) and (k, e’) add i to (j, e’) and (k, e) if |(j, e)|=1 remove j from 2(e) if |(j, e’)|=1 remove j from 0(e’) if |(j, e’)|=2 add j to 2(e’) if |(k, e’)|=0 add k to 0(e’) if |(k, e’)|=1 remove k from 2(e’) remove k from 0(e) goto step 1 April 3, 2000 Communication Networks C. D. u e; remove k from 0(u) if if |(j, u)|=2 remove j from 2(u) v sik swap sij with sik remove i from (j, u) and (k, v) add i to (j, v) and (k, u) if e<v if |(k, v)|=0 add k to 0(v) if |(k, v)|=1 remove k from 2(v) if |(j, v)|=1 remove j from 0(v) if |(j, v)|=2 add j to 2(v) goto step 1 if e>v u v goto step 5 B 31

Algorithm Complexity n adding an element to a set, choosing/removing the 1 st/2 nd element from a set take O(1) n steps 5 A 5 B and 5 D each take O(1) time n removing a generally positioned element from an r-set takes O(r) time step 5 C time complexity is in O(r) [ 2(v)-{k}, 0(v)-{j} ] n the looping in step 5 does not contain step 5 C, only 5 B and 5 D n the time complexity for step 5 is O(r) Algorithm time complexity O(nr 2) April 3, 2000 Communication Networks 32

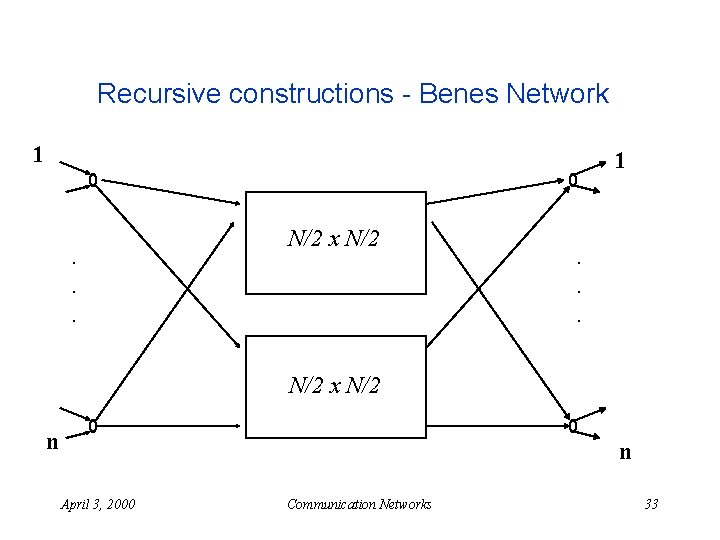
Recursive constructions - Benes Network 1 1 . . . N/2 x N/2 n n April 3, 2000 Communication Networks 33

Clos network size n Number of switching elements is given by n for k=n (rearrangeable non-blocking) n Optimal value for n is n=sqrt{2}N, which yields April 3, 2000 Communication Networks 34

a lower bound for the number of switching elements? n Assume we have 2 x 2 switching units. n We have N! switching permutation n Can we achieve this bound? April 3, 2000 Communication Networks 35

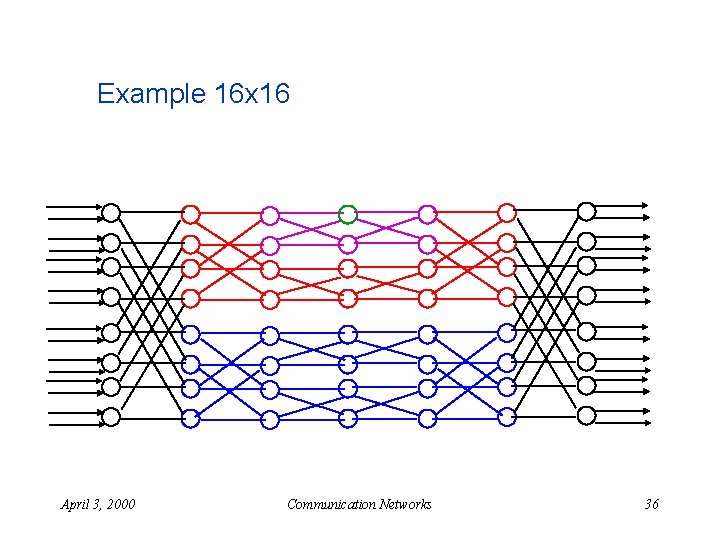
Example 16 x 16 April 3, 2000 Communication Networks 36

Benes Networks n Size: u u u n 2 log N – 1 stages N/2 switches in each stage N log 2 N –N/2 Rearrangeable u Clos network with k=2 n Symmetry n Example. n proof April 3, 2000 Communication Networks 37

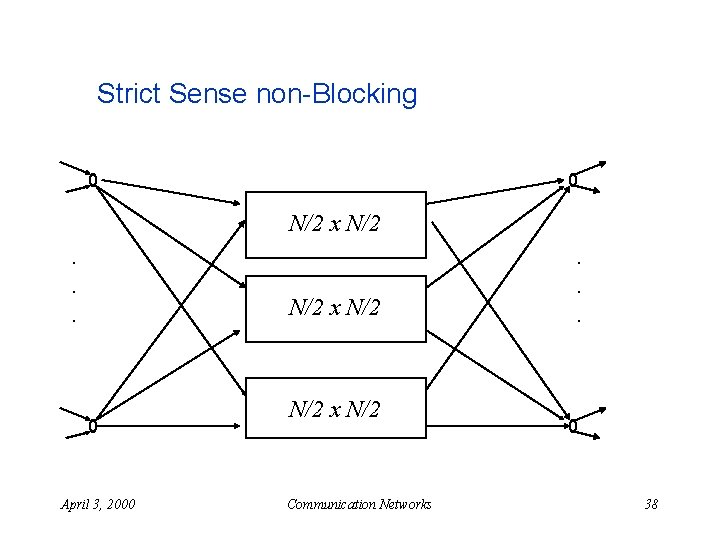
Strict Sense non-Blocking N/2 x N/2. . . N/2 x N/2 April 3, 2000 Communication Networks 38

Cantor Networks n m copies of Benes network. n For m >= log N its strict sense non-blocking n Network size N log 2 N n Example n Proof. April 3, 2000 Communication Networks 39

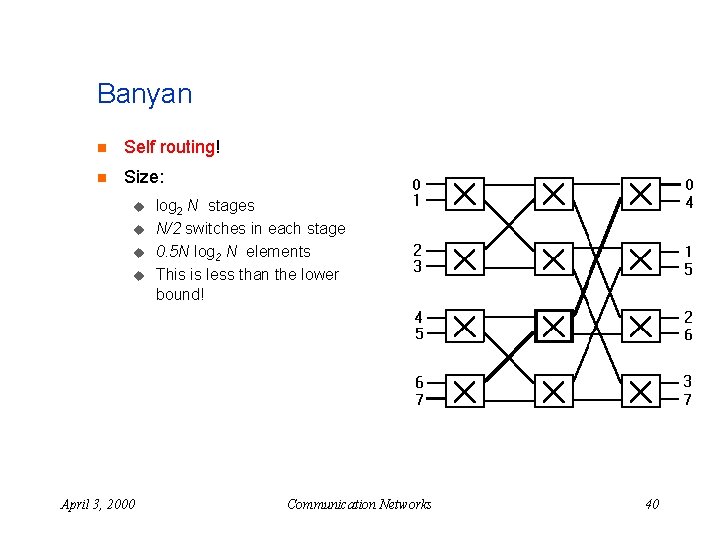
Banyan n Self routing! n Size: u u April 3, 2000 log 2 N stages N/2 switches in each stage 0. 5 N log 2 N elements This is less than the lower bound! Communication Networks 40

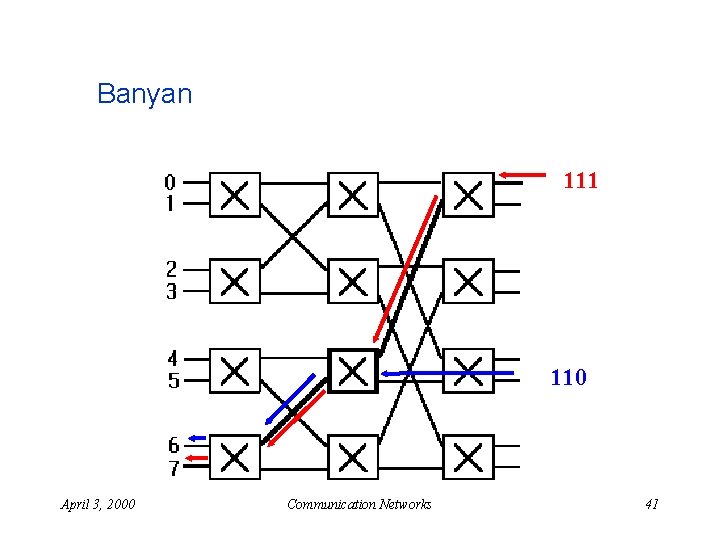
Banyan 111 110 April 3, 2000 Communication Networks 41

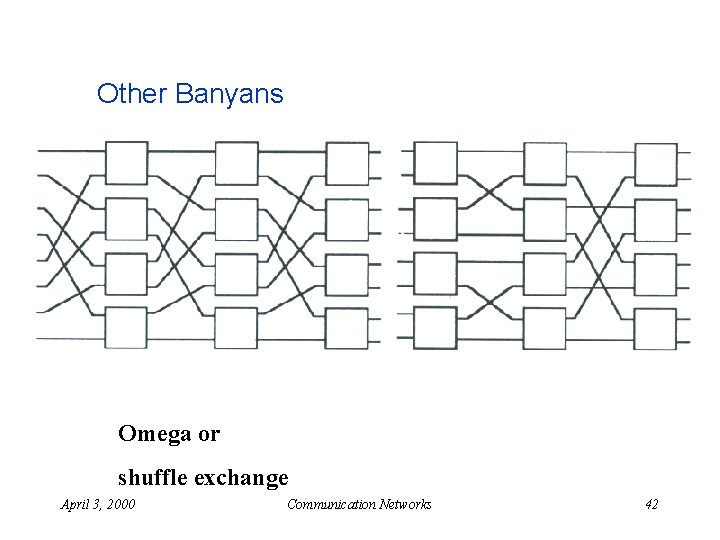
Other Banyans Omega or shuffle exchange April 3, 2000 Communication Networks 42

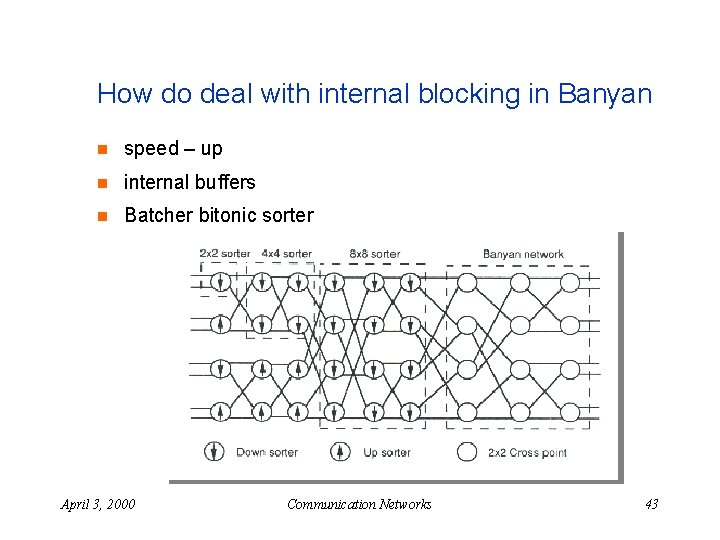
How do deal with internal blocking in Banyan n speed – up n internal buffers n Batcher bitonic sorter April 3, 2000 Communication Networks 43

April 3, 2000 Communication Networks 44