Switching circuits Composed of switching elements called gates

Switching circuits • Composed of switching elements called “gates” that implement logical blocks or switching expressions • Positive logic convention (active high): – High voltage or H – Low voltage or L Boolean 1 Boolean 0 • Negative logic convention (active low): – Low voltage or L – High voltage or H Boolean 1 Boolean 0

Switching circuits • Logic variables inputs/outputs “signals” • Signals “asserted” when the voltage level assumes the corresponding “ 1” value – Positive logic asserted by H – Negative logic asserted by L • Logic variables are written complemented when they are active low – Active high signals: – Active low signals: a, b, c ā, ē, ū

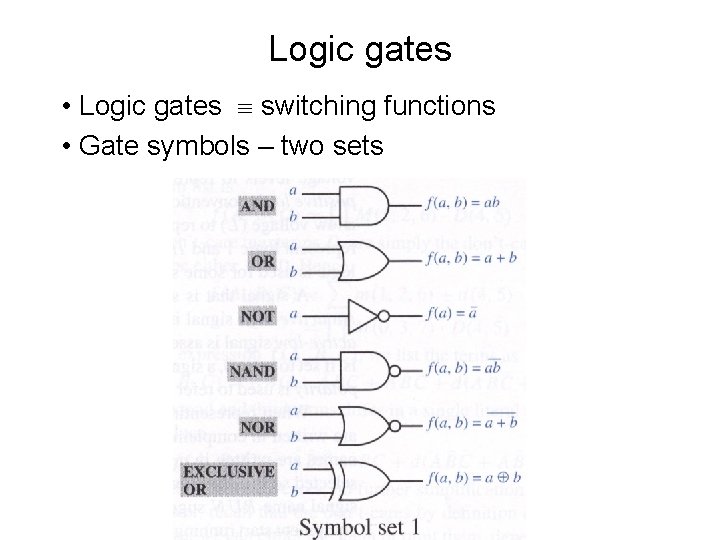
Logic gates • Logic gates switching functions • Gate symbols – two sets

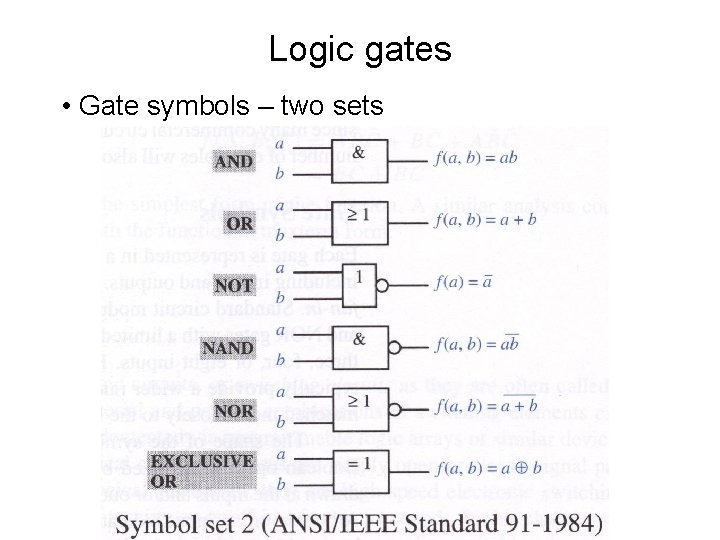
Logic gates • Gate symbols – two sets

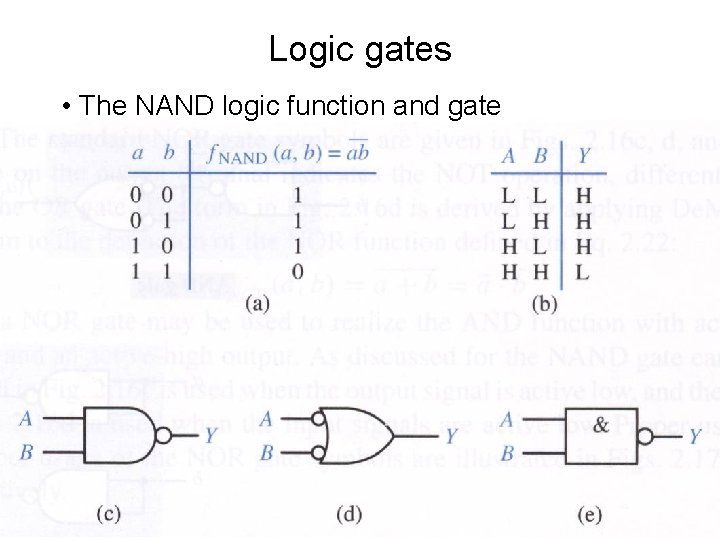
Logic gates • The NAND logic function and gate

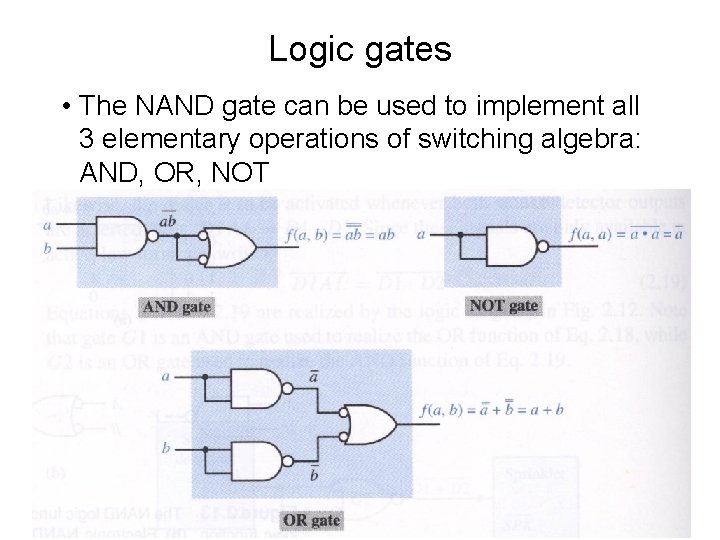
Logic gates • The NAND gate can be used to implement all 3 elementary operations of switching algebra: AND, OR, NOT

Logic gates • The set {AND, OR, NOT} implements any switching function (by definition): it is functionally complete • Therefore, the “NAND” gate can be used to implement any switching function – It is functionally complete, or “primitive”

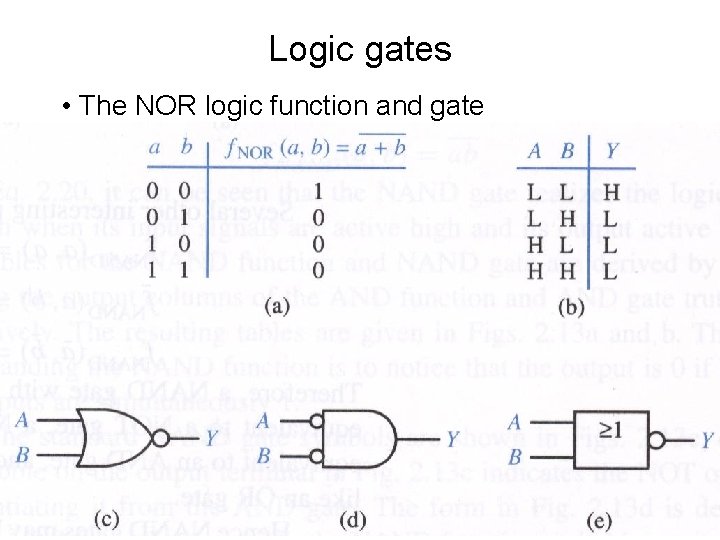
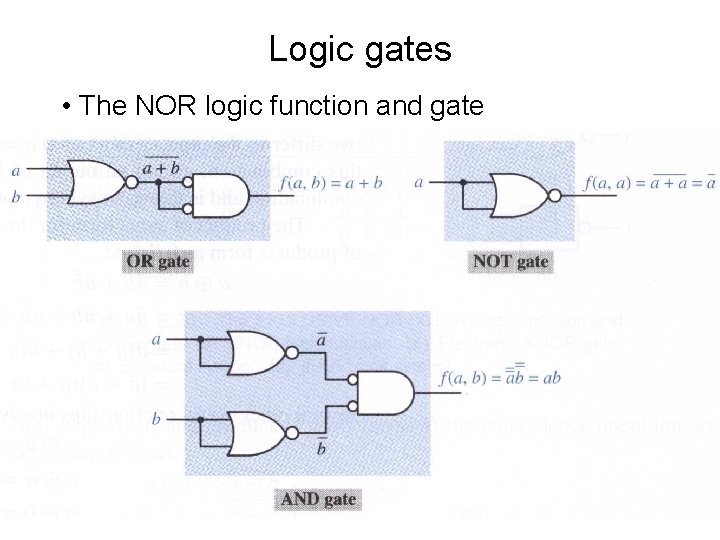
Logic gates • The NOR logic function and gate

Logic gates • The NOR function can be used to implement all 3 elementary operations of switching algebra: AND, OR, NOT – It is functionally complete too

Logic gates • The NOR logic function and gate

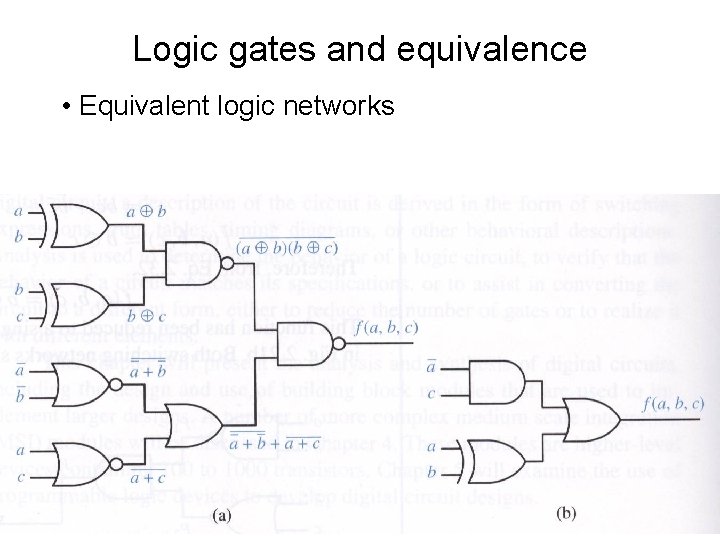
Logic gates and equivalence • CMOS is “inverting” logic – NOR and NAND are easier to implement than OR and AND – They are implemented as NOR or NAND followed by an inverter • More than one representation is possible for the same switching function • Different circuits of logic gates might perform the same switching function – Simpler networks are preferable – Need to analyze for equivalence and transform

Logic gates and equivalence • Equivalent logic networks

Logic gates and equivalence • Proving the equivalence

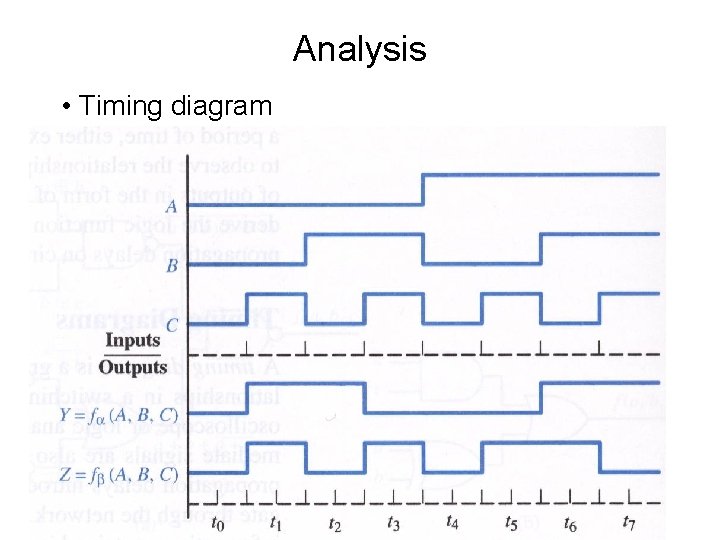
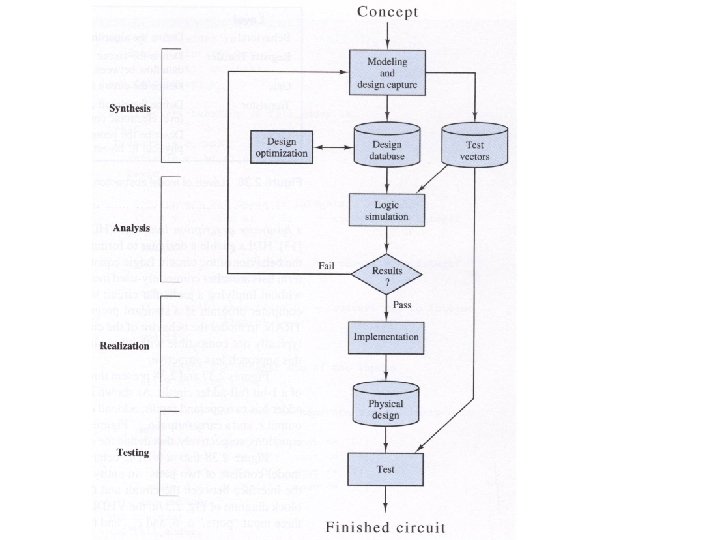
Digital circuits • Analysis – Given a circuit, abstract the Boolean function it is implementing and try to improve the implementation or verify the function • From gate diagrams • From timing diagrams • Synthesis – Given a switching function, obtain the corresponding switching network

Analysis • Timing diagram

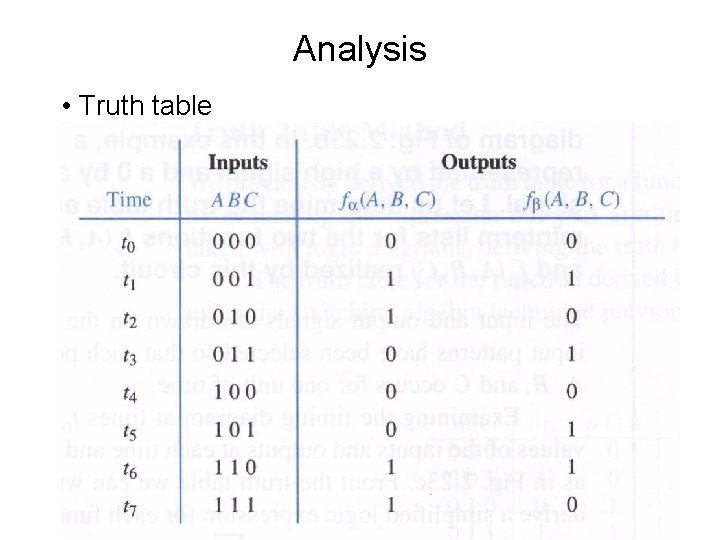
Analysis • Truth table

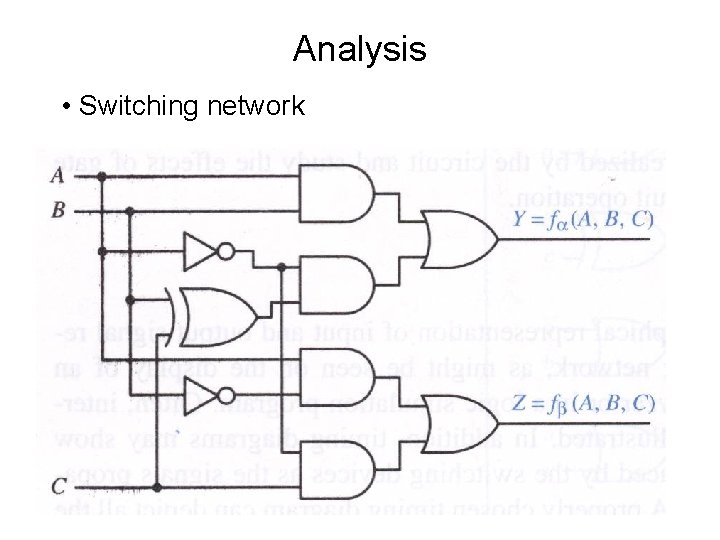
Analysis • Switching network

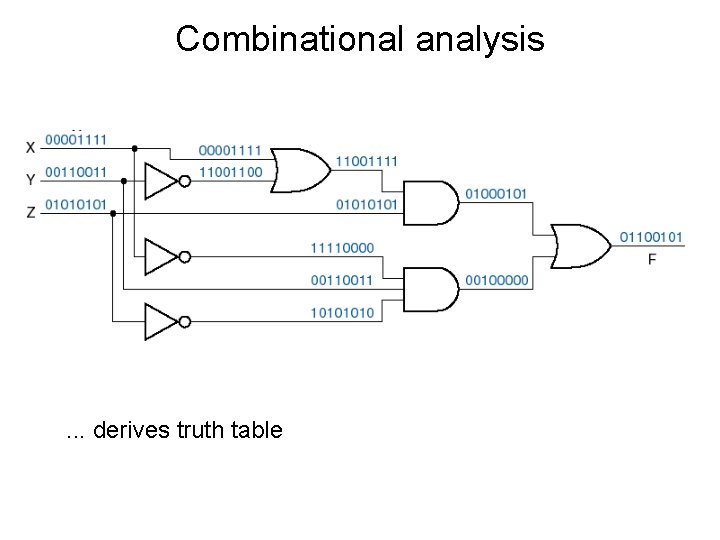
Combinational analysis . . . derives truth table

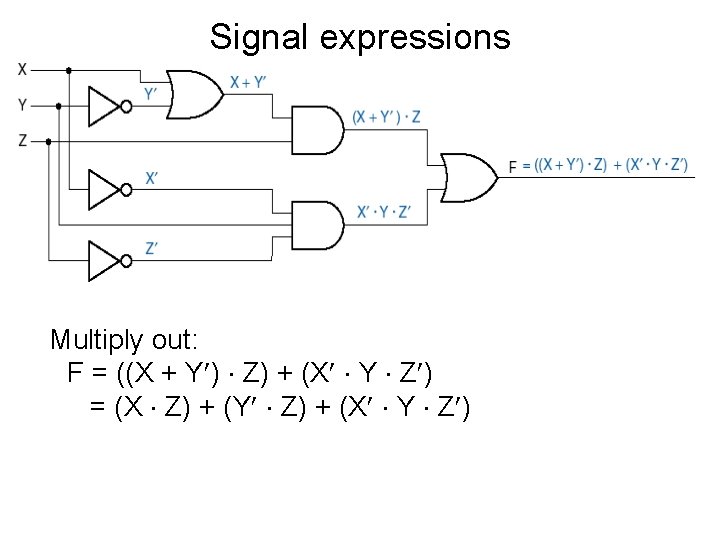
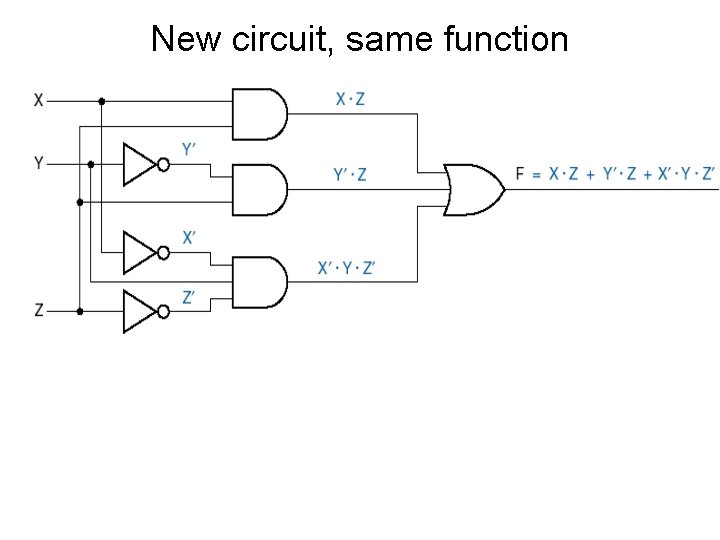
Signal expressions Multiply out: F = ((X + Y¢) × Z) + (X¢ × Y × Z¢) = (X × Z) + (Y¢ × Z) + (X¢ × Y × Z¢)

New circuit, same function

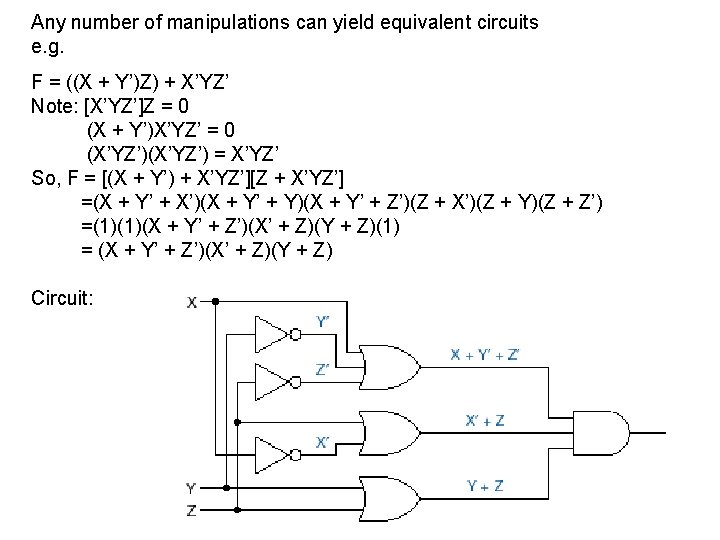
Any number of manipulations can yield equivalent circuits e. g. F = ((X + Y’)Z) + X’YZ’ Note: [X’YZ’]Z = 0 (X + Y’)X’YZ’ = 0 (X’YZ’) = X’YZ’ So, F = [(X + Y’) + X’YZ’][Z + X’YZ’] =(X + Y’ + X’)(X + Y’ + Y)(X + Y’ + Z’)(Z + X’)(Z + Y)(Z + Z’) =(1)(1)(X + Y’ + Z’)(X’ + Z)(Y + Z)(1) = (X + Y’ + Z’)(X’ + Z)(Y + Z) Circuit:

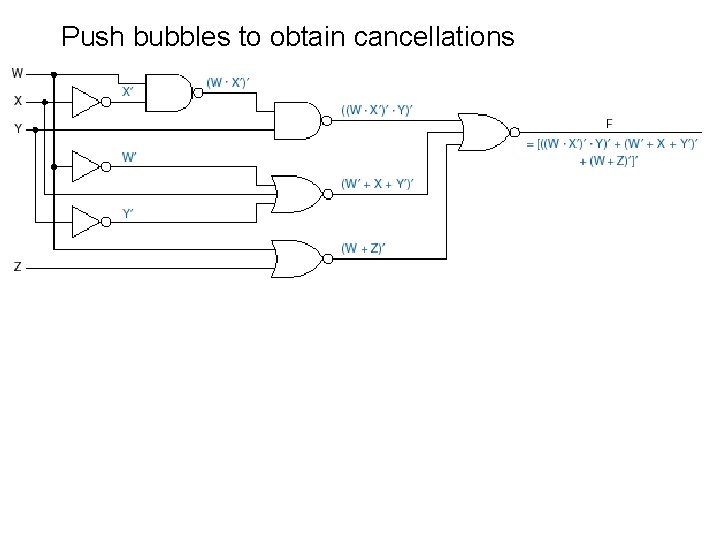
Push bubbles to obtain cancellations

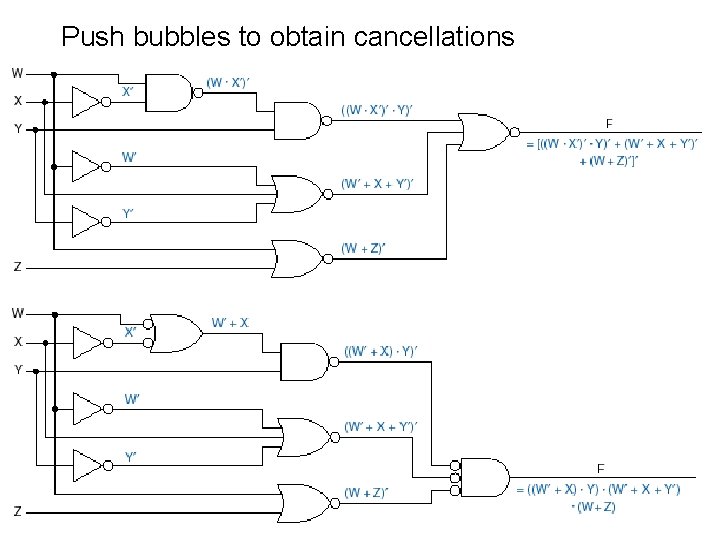
Push bubbles to obtain cancellations

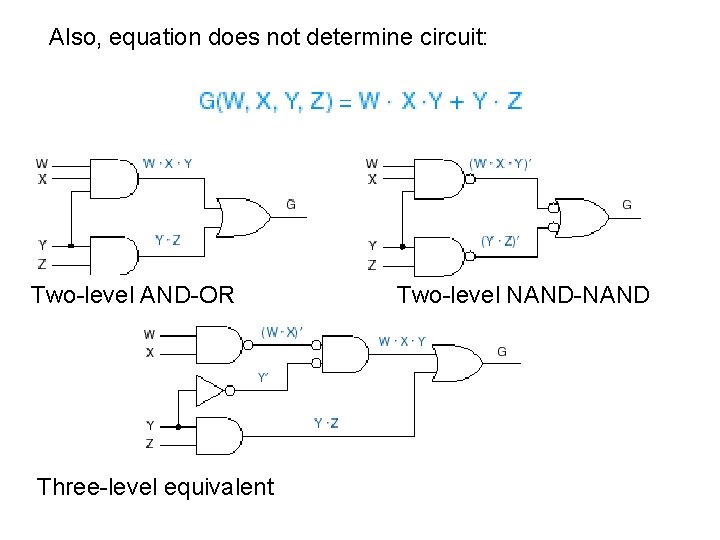
Conclude: given circuit ==> many equivalent equations circuit does not determine equation

Also, equation does not determine circuit: Two-level AND-OR Three-level equivalent Two-level NAND-NAND

Combinational analysis given circuit, determine function Combinational synthesis given function, determine circuit

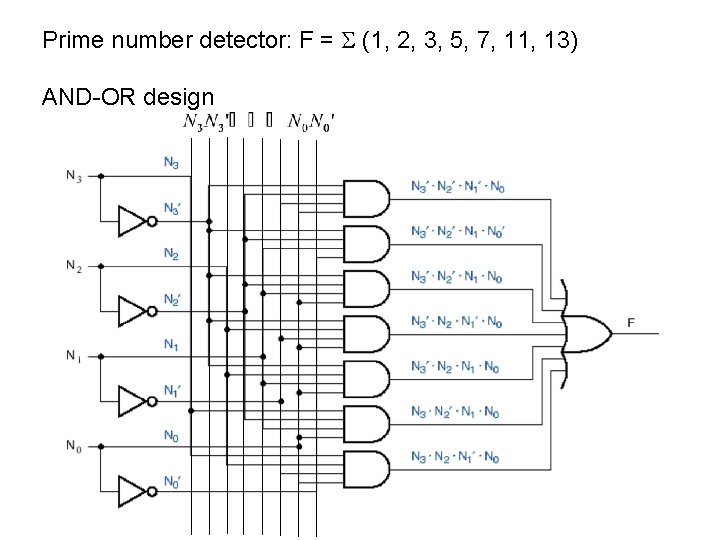
Prime number detector: F = (1, 2, 3, 5, 7, 11, 13) AND-OR design

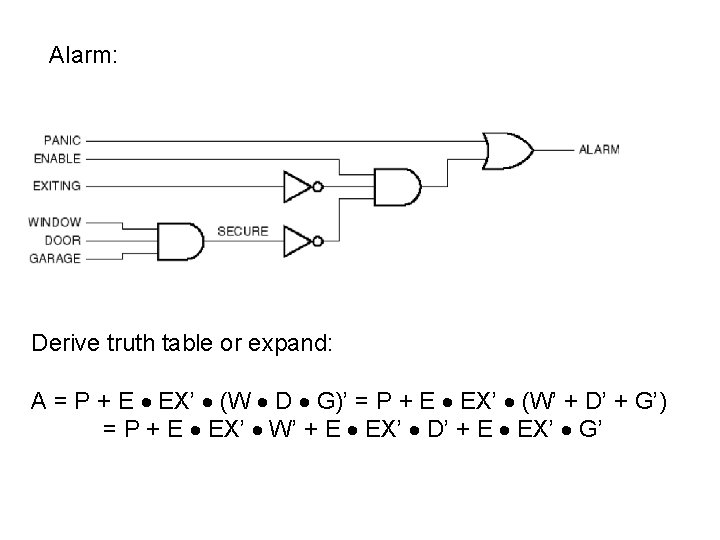
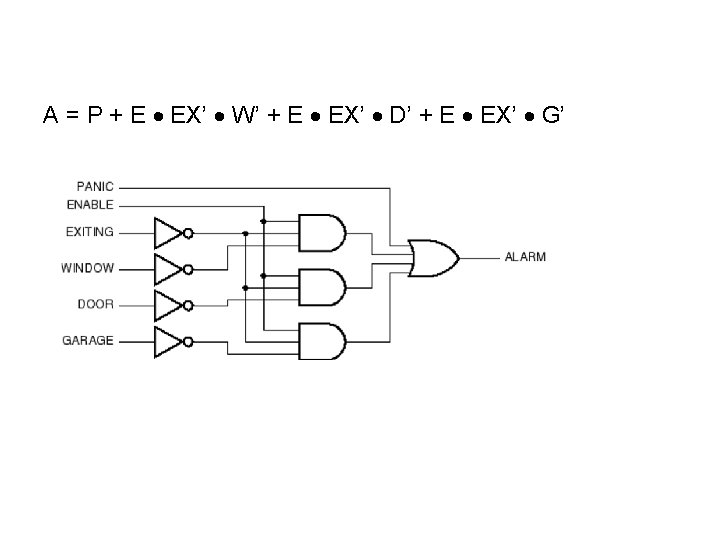
Alarm: Derive truth table or expand: A = P + E EX’ (W D G)’ = P + E EX’ (W’ + D’ + G’) = P + E EX’ W’ + E EX’ D’ + E EX’ G’

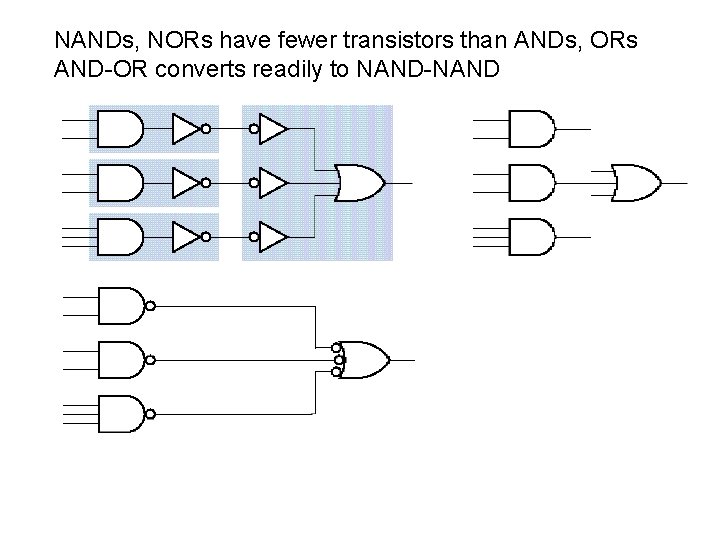
NANDs, NORs have fewer transistors than ANDs, ORs AND-OR converts readily to NAND-NAND

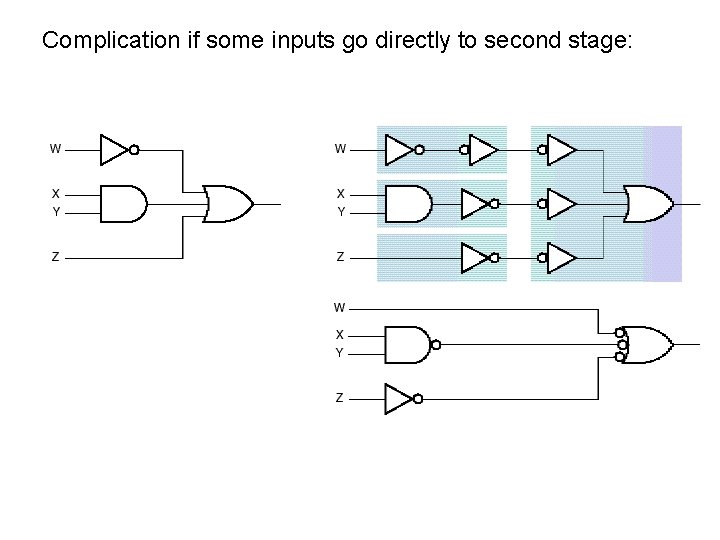
Complication if some inputs go directly to second stage:

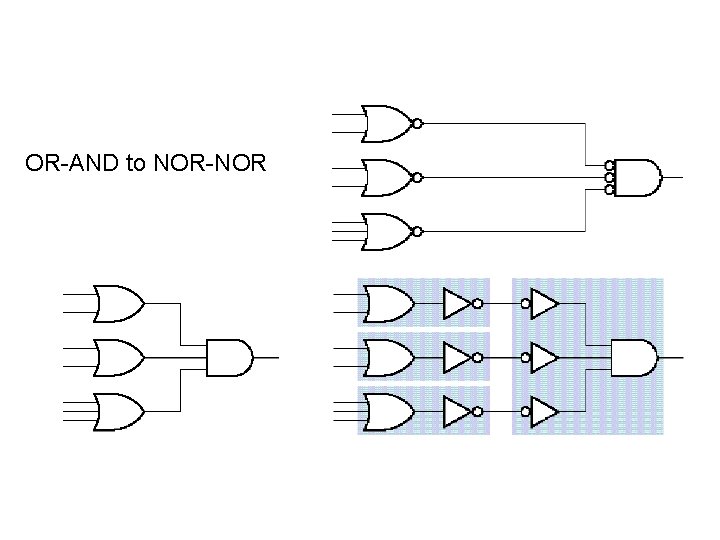
OR-AND to NOR-NOR

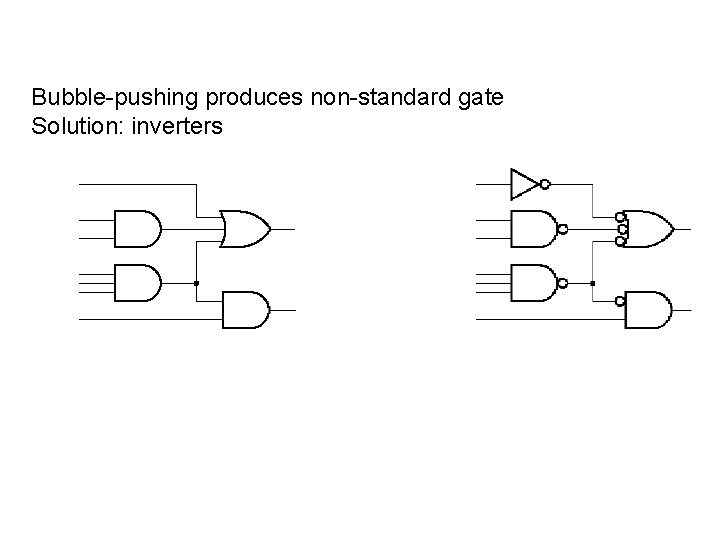
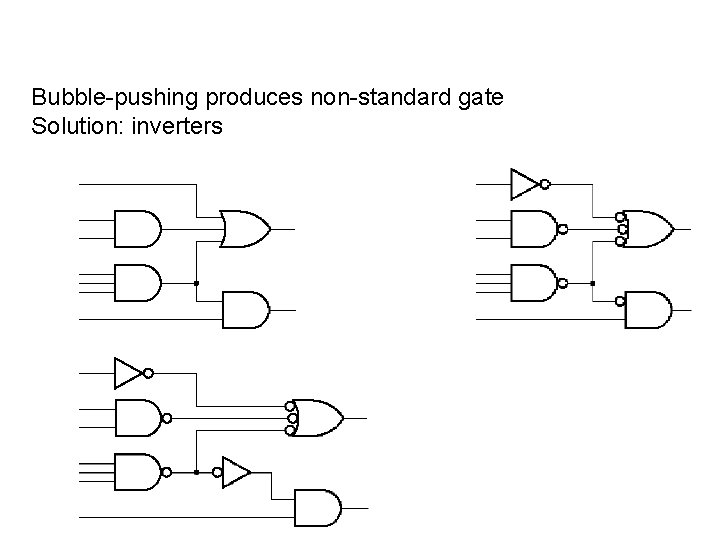
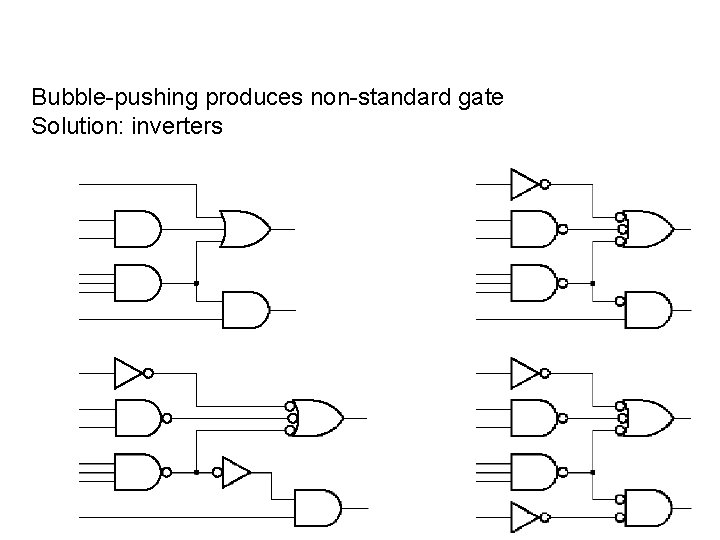
Bubble-pushing produces non-standard gate Solution: inverters

Bubble-pushing produces non-standard gate Solution: inverters

Bubble-pushing produces non-standard gate Solution: inverters

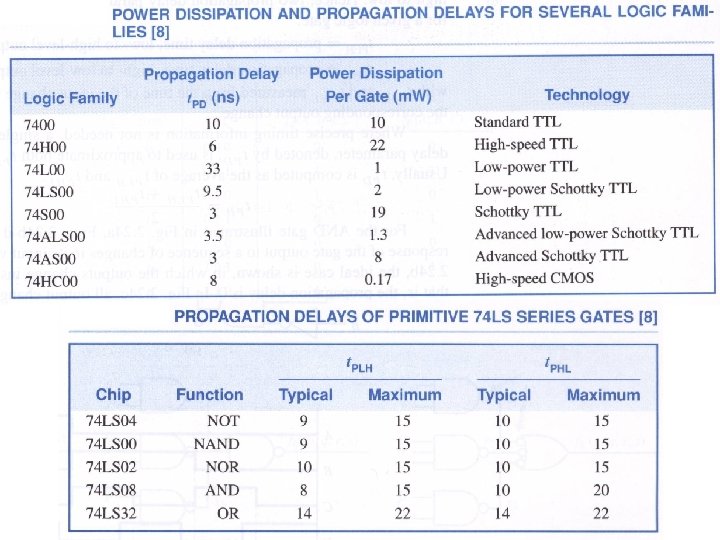
Propagation delay

Propagation delay

Synthesis • SOP functions -> AND – OR networks • POS functions -> OR – AND networks • Not always possible to design directly – Fan-in and out restrictions • Most designs are modular and multi-level • Modern designs are too complex • Design and testing by computers – VLSI - CAD

Logic simulation • Two states only for an ideal logic signal – Two gates driving the same line in opposite directions – Input left not connected or “floating” • Third state ‘X’ is added to the set of states • Truth tables change

Synthesis approaches illustrated to this point: Truth table derivation of minterms Ad hoc construction of logic equation Need systematic approach that minimizes hardware Karnaugh maps Quine-Mc. Cluskey algorithm