Swinburne Online Education Exploring the Solar System Module

Swinburne Online Education Exploring the Solar System Module 19: The Sun Activity 2: The Sun: Ruler of the Solar System © Swinburne University of Technology

Summary: In this Activity, we will investigate (a) the composition of the Sun. . . (b) the mass of the Sun. . . (c) how the Sun “works”. . . What is the Sun made of? What shape is it, and why? . . . and the masses of other stars and planets … how the mass of the Sun can be measured …at least, how people used to think that the Sun produces energy

(a) What the Sun is made of. . . We’ll start by learning what the Sun is composed of. The composition of the Sun will help to explain why the Sun is the shape it is, and (in the next Module) how the Sun manages to emit such an enormous amount of energy over such an incredible length of time.

Composition of the Sun The average density of the Sun is 1410 kg m-3 (kilograms per cubic metre), ranging from 160, 000 kg m-3 at the core to almost nothing at the corona. For comparison: Sun 1410 kg m-3 Jupiter 1400 kg m-3 Saturn 690 kg m-3 H HO HHe HC H HHe. H C O HH He H HHHe Earth Mars Moon Why is it so? The diagram to the left might give you a hint … 5520 kg m-3 3900 kg m-3 3340 kg m-3 What do the H, He, O and C mean?

The reason: some objects in the Solar System are mostly solid and comprised of heavier elements, while other objects are comprised entirely or almost entirely of gas. Even if that gas is sometimes extremely compressed, it is far less dense than a solid made of heavier elements. It is pretty obvious which of the bodies listed below consist mostly of gas. “Jovian”, mostly gas Sun 1410 kg m-3 Mercury 5440 kg m-3 Jupiter 1340 kg m-3 Venus 5240 kg m-3 Saturn 690 kg m-3 Earth 5497 kg m-3 Uranus 1190 kg m-3 Moon 3360 kg m-3 Neptune 1660 kg m-3 Mars 3940 kg m-3 Pluto (uncertain: 2000? ) “Terrestrial”, mostly solid

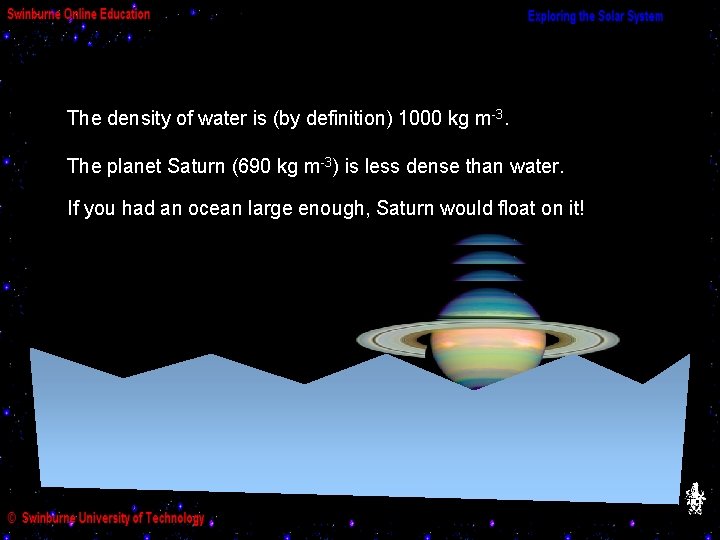
The density of water is (by definition) 1000 kg m-3. The planet Saturn (690 kg m-3) is less dense than water. If you had an ocean large enough, Saturn would float on it!

The Sun is made up almost entirely of hydrogen (72%) and helium (26%), while other elements make up the remaining 2%. For example, for every million hydrogen atoms in the Sun, there about 90, 000 helium atoms … and only about 690 oxygen 420 carbon 87 nitrogen 45 silicon 40 magnesium 37 neon 32 iron (and traces of many others)

(b) Mass of the Sun The mass of the Sun is 1. 989 x 1030 kg, or about 300, 000 times that of the Earth. However, the radius of the Sun is about 100 times that of the Earth; therefore, its volume is about 1, 000 times that of Earth. The reason: the Sun is made up mostly of light elements such as hydrogen and helium, while the Earth is made mostly of heavy elements such as iron.

Measuring the Mass of the Sun How on Earth can we measure the mass of the Sun? It is not possible to “weigh” the Sun, but its effect on the planets can be used to estimate its mass. To understand this further, we will have to have a look at gravitational force and how it depends on mass.

Newton’s Law of Gravitational Attraction Isaac Newton discovered an important fact about gravitational force a long time ago. If two bodies share a gravitational attraction, the force of attraction depends on both of their masses. Show me the equation! On Earth, we call this gravitational attraction “weight”. It depends on the masses of both the planet and the object you are weighing.

Weight depends on where you are m M m 2 m 600 N Chris feels a gravitational force of 600 N on Earth. M 1200 N If Chris doubles in mass, the gravitational force will double: 1200 N. 1/80 M 0. 27 R 100 N If, on the other hand, Chris moves to the Moon, which has a smaller mass and radius, the gravitational force will decrease by 5/6 to 100 N. To remind you again: if any two bodies share a gravitational attraction, that attraction depends on the masses of both of them and their separation (in fact its another inverse square law).

Interesting, but … we need more! Now, this principle is very useful in astronomy. If we know In practice astronomers combine Newton’s lawthe of distance gravitation to the Sun, the velocity with his other laws, like F=ma (Force is equal to mass times of the Earth and Newton’s acceleration) and the fact that in order to stay circular motion Constant we in calculate the force required is mv 2/R where m, the v and R are the. Sun mass, mass of the ! velocity and distance to an object. Force to The basic idea is that the gravitational force between Gravitational a objects must equal theremain force in required to keep the objects Force circular in their orbits. If one star orbit! is very much heavier than the other:

Kepler’s Third Law Kepler discovered that the planets travel around the Sun in such a way that the time required to complete one orbit was independent of their mass, and only dependent upon their distance from the Sun. The same is true for the orbit of satellites around the Earth, i. e. it depends only on the mass of the Earth and the satellite distance — and not on the mass of the satellite at all! R = radius of orbit, the distance between the planet and the star T = period of orbit, the time taken to complete one revolution (i. e. a “year”) Kepler’s third law states is constant.

Same radius, same period Astronauts in satellites and their lunches have very different masses, but that doesn’t matter. Because they are at the same radius, they have the same period of revolution. Just as well: otherwise astronauts would lose their lunch (and anything else they didn’t hang on to) quick smart. Comment: The relationship between the orbit of a planet and the mass of its “parent” star is promising.

Therefore, measuring the orbits of the planets (that is, radius R and period T) can allow us to calculate the mass of the Sun (provided that you know what the constant G is) This is why scientists in the 18 th century were so keen to measure the distance to the Sun! Newton’s laws, coupled with an accurate distance to the Sun, led to the first measurements of its mass of 2 x 1030 kg. Newt on rules OK!

The Sun is so much more massive than anything else in the Solar System. 1 Earth mass Jupiter: 318 Earth masses Sun: 300 000 Earth masses (and not to scale!)

Masses of other bodies: binary systems If the masses of two bodies orbiting each other are not too different (e. g. in a binary star system, or the Earthand-Moon system) the masses of the two bodies can be compared by measuring “perturbation” in their motions. Click on the corresponding picture below to view animation.

Two possible ways to measure mass In summary: The period and radius of orbit of a planet about a star depend only on the mass of the star. This fact is useful in the Solar System, as period and radius of orbit are not too hard to measure. If two bodies aren’t too different in mass, each clearly revolves around the other. Comparing the radii of their orbits allows you to compare their masses. This fact is one of the key factors that helped astronomers measure the masses of other stars - more later.

Shape of the Sun Some ancient peoples believed that the Sun was round. . . … because it was a huge ball of dung being rolled across the sky by a beetle! There actually three forces affecting the shape of the Sun, causing it to be an oblate spheroid: that is, a sphere or ball that is slightly squashed.

The three things that define the Sun’s shape are: The gravitational forces between the atoms in the Sun, causing it to collapse. . . (these forces will decrease as the Sun loses mass) The pressure of gas within the Sun, causing it to expand… (this will depend on the temperature of the Sun) The rotation of the Sun on its axis, causing it to “belly out” around its equator. (this should stay about the same during the Sun’s main sequence lifetime)

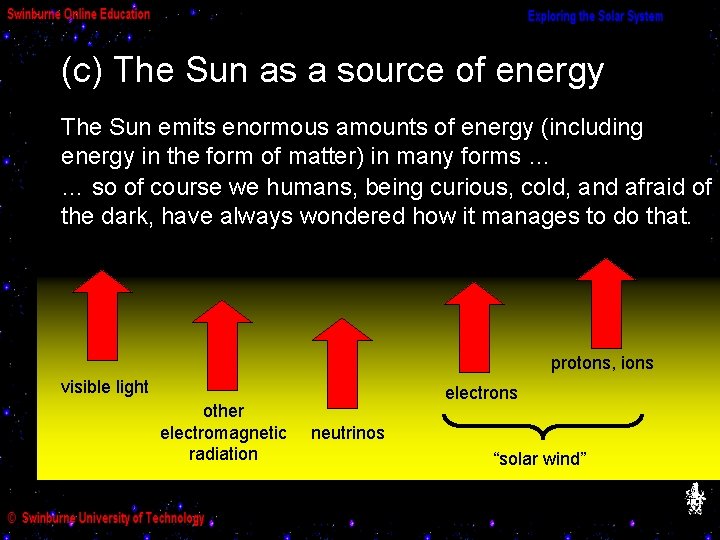
(c) The Sun as a source of energy The Sun emits enormous amounts of energy (including energy in the form of matter) in many forms … … so of course we humans, being curious, cold, and afraid of the dark, have always wondered how it manages to do that. protons, ions visible light other electromagnetic radiation electrons neutrinos “solar wind”

How the Sun works Many humans thought for thousands of years that the Sun was actually a ball of flame: that is, that the heat and light from the Sun came from chemical reactions, just like the heat and light from a fire. This cannot be so. It can be shown that if the Sun were fuelled by chemical reactions it could never have survived for anything approaching 5 billion years. It would have burned up long ago.

Later on, when people became more familiar with gases and the relationship between volume, temperature and pressure, they thought that the Sun was radiating heat and light because of gravitational contraction. Squeeze a ball of gas. . . … and it gets hotter However, if this were so, the Sun could have managed to radiate heat and light for only 15 million years … and radioactive dating and other evidence suggests that our Solar System is already about 5 billion years old.

Neither chemical combustion nor gravitational collapse could account for the enormous energy output and the extended lifetime of the Sun. It was only very recently (in terms of the history of science) that people came up with another, newer idea to explain how the Sun works…

… and that deserves just about a whole chapter to itself. So we’ve continued the story in the next Activity, Solar is Nuclear.

The Sun in Summary 1

The Sun in Summary 2

Image Credits Burning pallets (reproduced with permission) http: //flame. cfr. nist. gov/fires/pall/pa_840. gif Johannes Kepler (reproduced with permission) http: //antwrp. gsfc. nasa. gov/apod/ap 970913. html Solar disk in broadband K Ca lines Data courtesy of J. Harvey, National Solar Observatory (Tucson/Kitt Peak, AZ). http: //www. hao. ucar. edu/public/slides/slide 2. html NASA: Blue sun http: //sohowww. nascom. nasa. gov/bestofsoho/ NASA: Transition Region and Coronal Explorer (TRACE) recording of the Sun at 171 Angstrom, 24/8/98 http: //sohowww. nascom. nasa. gov/data/synoptic/gif/980824/stra_00171_fd_19980824_1203. gif HST: Saturn (colour-enhanced) http: //oposite. stsci. edu/pubinfo/pr/1998/18/content/9818 x. jpg

Now return to the Module home page, and read more about the Sun in the Textbook Readings. Hit the Esc key (escape) to return to the Module 19 Home Page

Chemical symbols An element is a pure substance, containing only one kind of atom (that is, all atoms in this substance have the same number of protons). H = hydrogen He = helium O = oxygen When astronomers, chemists, biologists and other people working in the sciences want to write about particular elements such as hydrogen, helium, oxygen and so on, they use a letter or letters which relate to the Latin name for the substance. C = carbon Example: CO 2 = carbon dioxide

Back to “Composition of the Sun”

Gravitation: the equations The equations that describe the gravitational force between two objects with mass were first developed by Sir Isaac Newton (late 1600 s). Under most circumstances these well-established laws are perfectly adequate in describing what we observe; it is only when extremely massive or fast-moving objects are involved that we have to use the relativistic equations of Albert Einstein instead.

Force between two objects with mass Isaac Newton’s law of gravitation: The gravitational force between two objects separated by a distance R, one with mass M and the other with mass m, is given by: G is the Universal Gravitational Constant

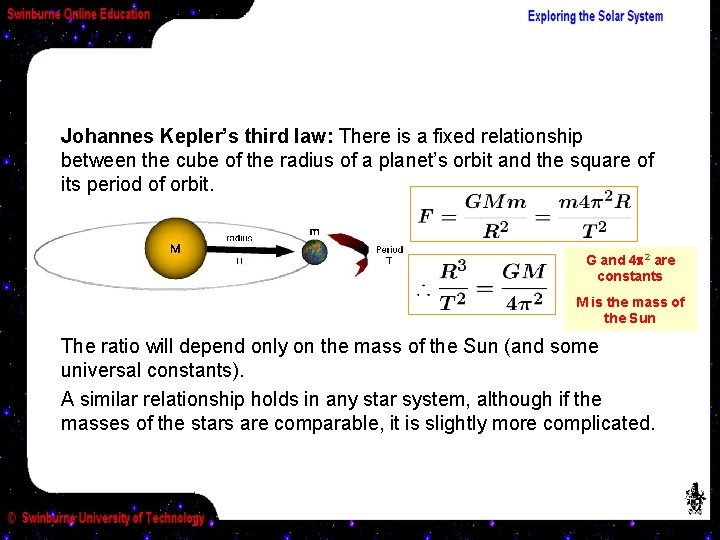
Johannes Kepler’s third law: There is a fixed relationship between the cube of the radius of a planet’s orbit and the square of its period of orbit. G and 4 p 2 are constants M is the mass of the Sun The ratio will depend only on the mass of the Sun (and some universal constants). A similar relationship holds in any star system, although if the masses of the stars are comparable, it is slightly more complicated.

Johannes Kepler lived from 1571 to 1630, completing most of his most profound and useful work after 1601, in Prague. First Law: The orbits of planets are ellipses, with the Sun at one focus. Second Law: A line from a planet to the Sun sweeps out equal areas in equal times. Third Law: The cube of the radius of a planet’s orbit is directly related to the square of its period of orbit. [Alternatively, the quotient of these is constant, within one solar system. ] G and 4 p 2 are constants M is the mass of the Sun

Back to “Measuring the Mass”