Sweep Line Algorithms Problem Visualization Etc Cp Sc

Sweep Line Algorithms, Problem Visualization, Etc. Cp. Sc 212: Algorithms and Data Structures Brian C. Dean School of Computing Clemson University Fall, 2013

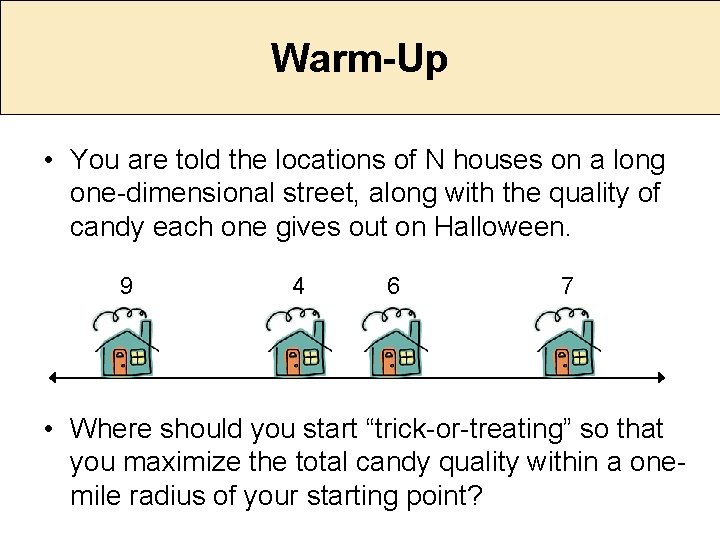
Warm-Up • You are told the locations of N houses on a long one-dimensional street, along with the quality of candy each one gives out on Halloween. 9 4 6 7 • Where should you start “trick-or-treating” so that you maximize the total candy quality within a onemile radius of your starting point?

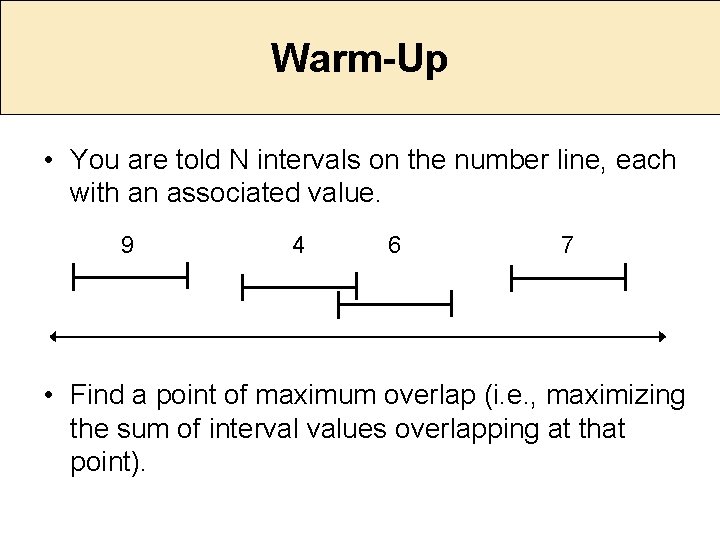
Warm-Up • You are told N intervals on the number line, each with an associated value. 9 4 6 7 • Find a point of maximum overlap (i. e. , maximizing the sum of interval values overlapping at that point).

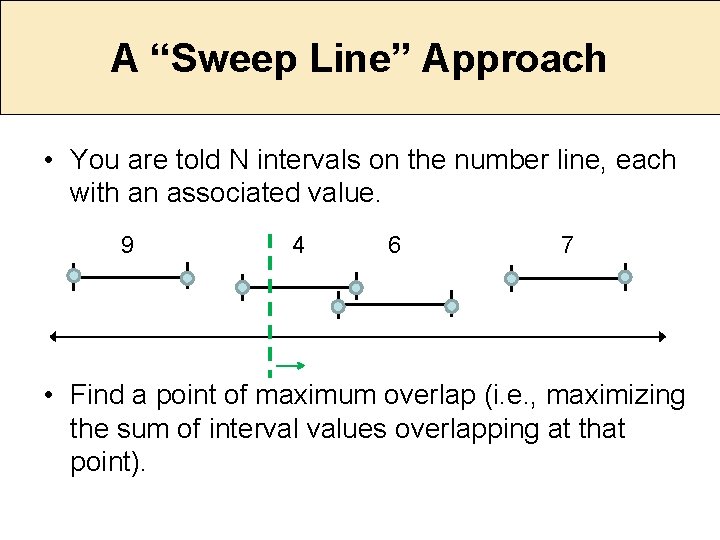
A “Sweep Line” Approach • You are told N intervals on the number line, each with an associated value. 9 4 6 7 • Find a point of maximum overlap (i. e. , maximizing the sum of interval values overlapping at that point).

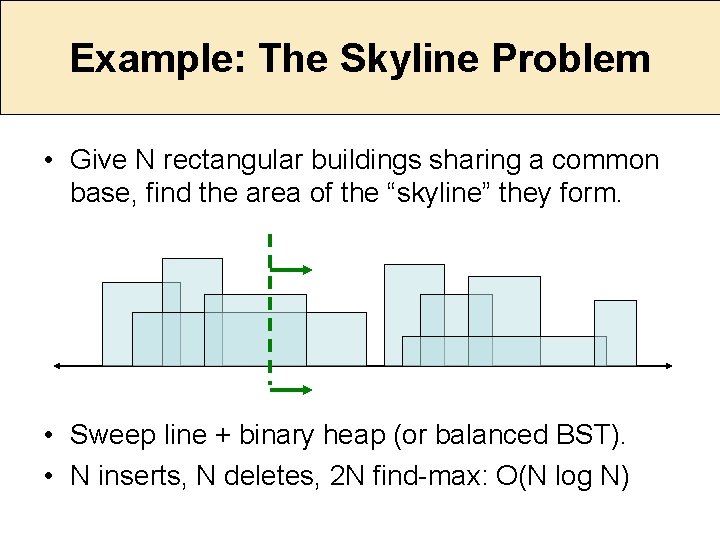
Example: The Skyline Problem • Give N rectangular buildings sharing a common base, find the area of the “skyline” they form. • Sweep line + binary heap (or balanced BST). • N inserts, N deletes, 2 N find-max: O(N log N)

Counting Intersection Points Among Axially-Aligned Segments

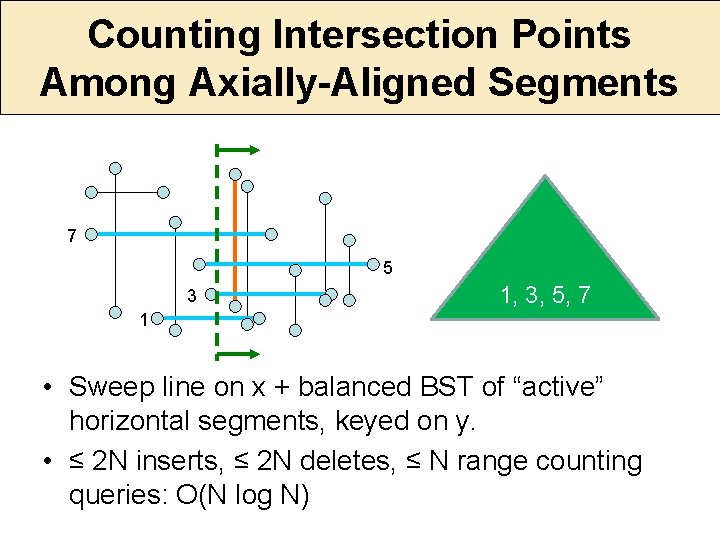
Counting Intersection Points Among Axially-Aligned Segments 7 5 3 1, 3, 5, 7 1 • Sweep line on x + balanced BST of “active” horizontal segments, keyed on y. • ≤ 2 N inserts, ≤ 2 N deletes, ≤ N range counting queries: O(N log N)

Non-Dominated Points

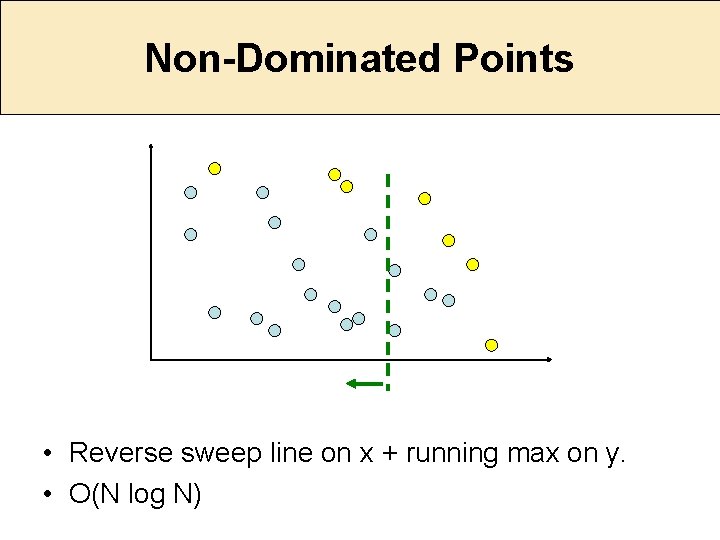
Non-Dominated Points • Reverse sweep line on x + running max on y. • O(N log N)

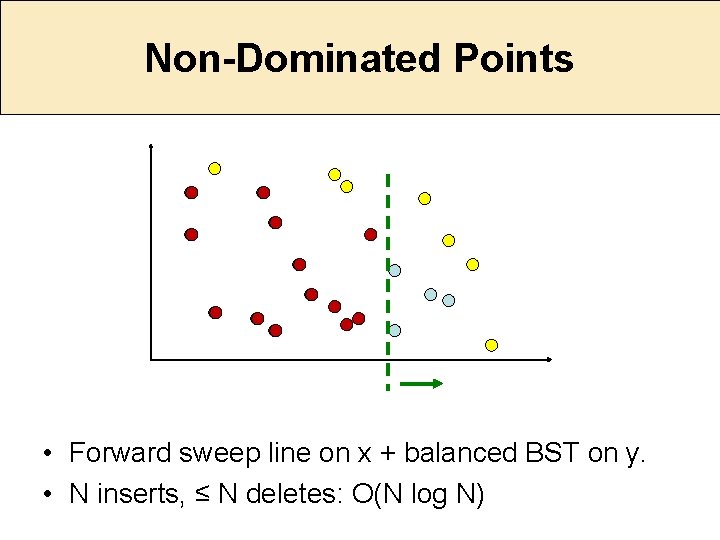
Non-Dominated Points • Forward sweep line on x + balanced BST on y. • N inserts, ≤ N deletes: O(N log N)

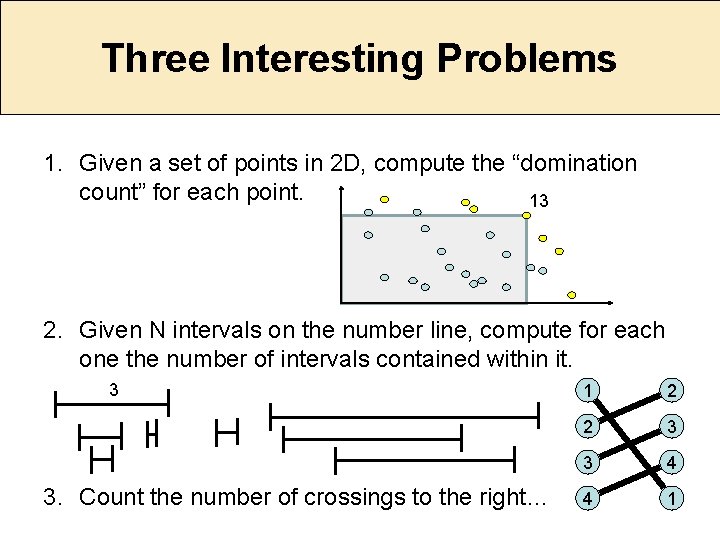
Three Interesting Problems 1. Given a set of points in 2 D, compute the “domination count” for each point. 13 2. Given N intervals on the number line, compute for each one the number of intervals contained within it. 3 3. Count the number of crossings to the right… 1 2 2 3 3 4 4 1

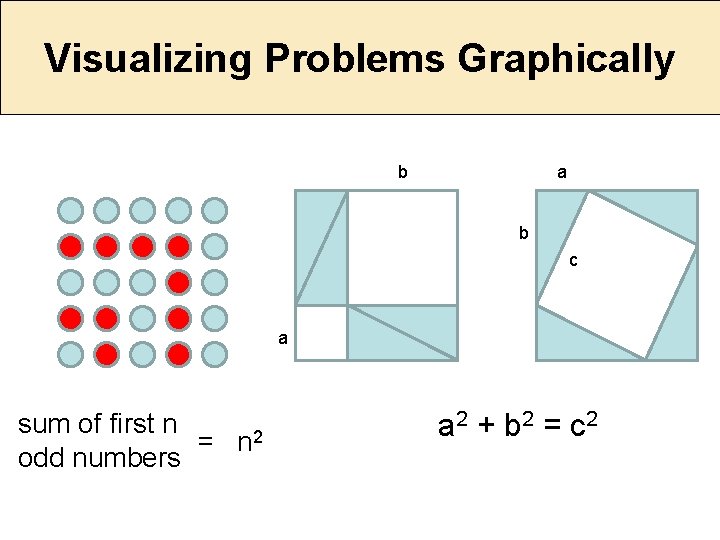
Visualizing Problems Graphically b a b c a sum of first n = n 2 odd numbers a 2 + b 2 = c 2

Robot Arms, Databases, and “Parameter Space” • Suppose a robot arm has 4 movable joints, each with one degree of freedom. You want to move the arm from its current state to a new “goal” state, where certain joint configurations are not valid. path finding in a 4 D space. • Consider a database of N records where each contains fields (height, age, income). set of points in 3 D space.

Ballroom Matching • You are given the height and weight of N boys and N girls. • In a ballroom matching class, you want to match each girl with a boy who is taller and heavier than he is (to allow for easy lifts). • How quickly can you determine a valid matching between the boys and girls (or that none exists)?

Pumpkin Catching • You are told when and where N pumpkins will fall from a pumpkin tree onto a number line. (e. g. , “Pumpkin #1 lands at time t = 4 at the point x = 5). • You are also told where your N friends are standing on the number line at time t = 0. • Each friend can move at one unit of distance per second and can catch at most one pumpkin (they are heavy, after all!) • Can your team catch all the pumpkins?