Suwak logarytmiczny Agnieszka Dydacka Katarzyna Siejek Instytut Matematyczny

Suwak logarytmiczny Agnieszka Dydacka, Katarzyna Siejek Instytut Matematyczny, specjalność nauczycielska, III rok

Plan prezentacji 1) 2) 3) 4) 5) 6) Dodawanie i odejmowanie na suwaku Wynalazek logarytmu Mnożenie i dzielenie na suwaku Inne działania na suwaku Dokładność obliczeń Typy suwaków

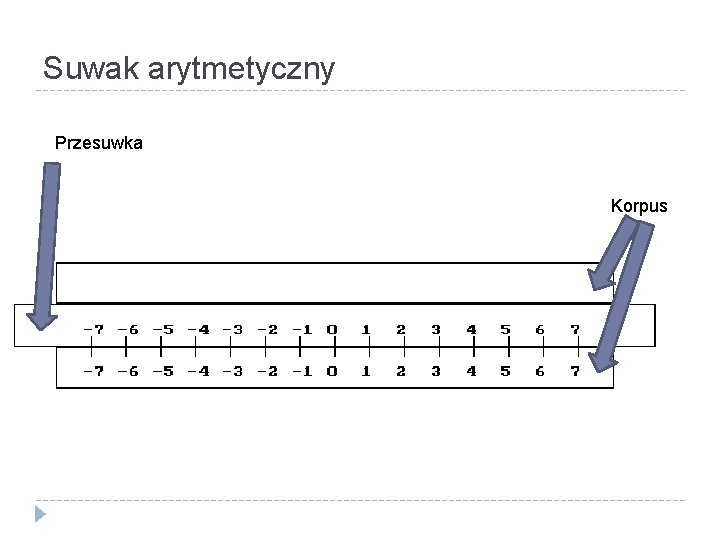
Suwak arytmetyczny Przesuwka Korpus

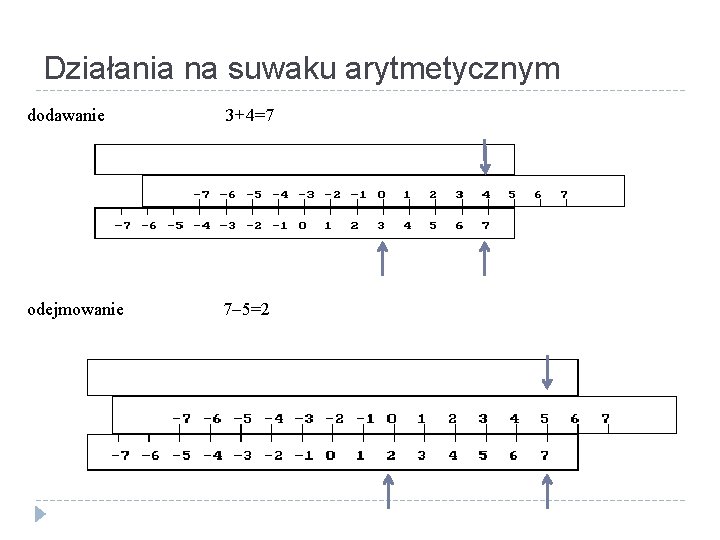
Działania na suwaku arytmetycznym dodawanie 3+4=7 odejmowanie 7 5=2

Działania odwrotne

Wynalezienie logarytmu John Napier (1550 – 1617)

Ćwiczenia na logarytmach 2 a) log 3 9 =. . . . 4 b) log 5 625 =. . . . 32 = 5 c) log 2. . . . 10 100 = 2 d) log. . . . e) log. . . . 4 4 = 1 -1 f) log 2 0. 5 =. . . . -2 g) log 1/5 25 =. . . . 4 = -2 h) log ½. . . . i) log. . . . 1/10 100 = -2 -3 j) log ½ 8 =. . . . 0 k) log 7 1 =. . . . 1 =0 l) log . . . . m) log. . . = 3 n) log. . . . 49 =. . . . o) log. . . . 0. 01 =. . . . p) log. . . = 1 r) log. . . =. . . .

Mnożenie jako dodawanie

Dzielenie jako odejmowanie

Własności logarytmu

Własności logarytmu

Suwak jako przyrząd Suwak logarytmiczny Faber Castell 2/83 N

Krótka historia suwaka • 1620 – wynaleziony przez Edmunda Guntera • 1632 – ulepszony przez Wiliama Oughtreda • różne typy – walec, koło, prosta linijka • 1750 – postać linijki z ruchomą listewką • powszechnie używany do lat 70. XX wieku William Oughtred (1574 – 1660)

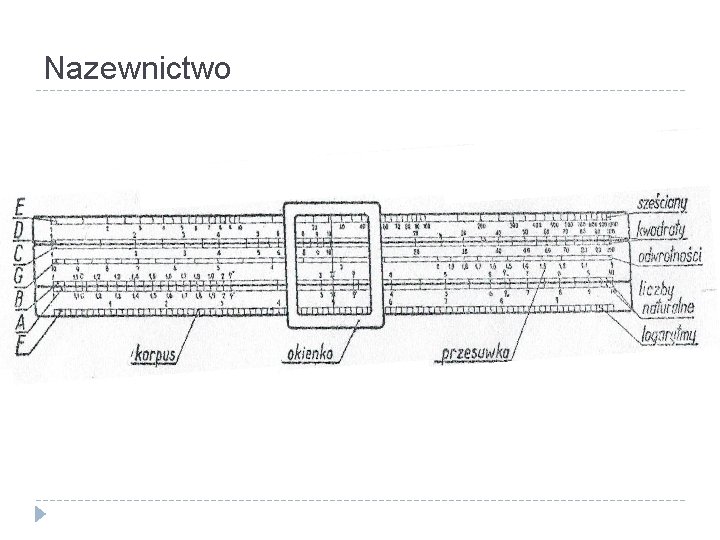
Nazewnictwo

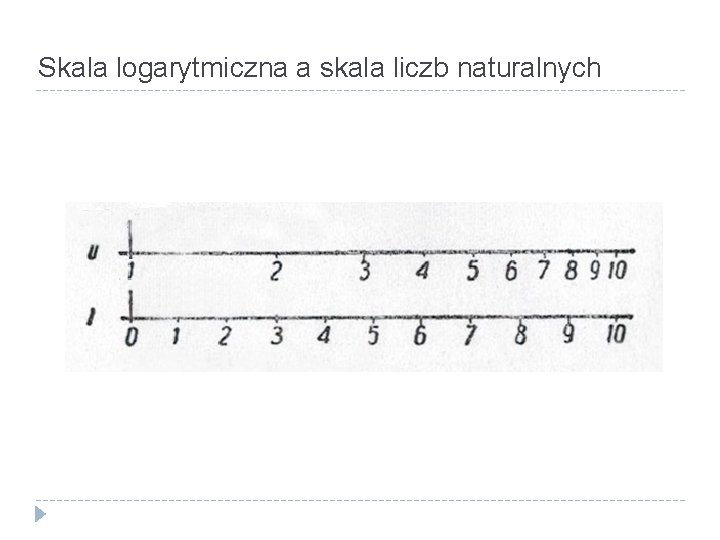
Skala logarytmiczna a skala liczb naturalnych

Skale potęg Skala n-tej potęgi jest n-krotnie gęstsza.

Rząd wielkości liczby • a≥ 1 liczba cyfr przed przecinkiem z plusem, • 0<a<1 liczba zer po przecinku z minusem liczba 123, 4 12, 34 1, 234 0, 1234 0, 0123 0, 0012 0, 0001 rząd wielkości +3 +2 +1 0 -1 -2 -3

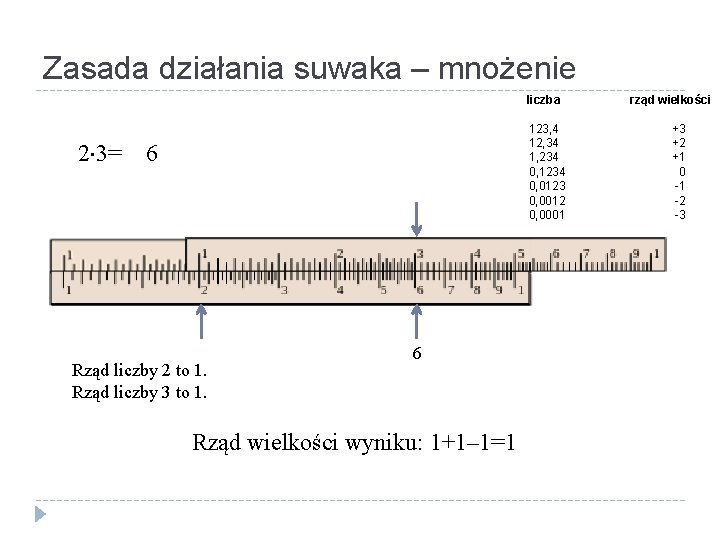
Zasada działania suwaka – mnożenie liczba 2 3= 123, 4 12, 34 1, 234 0, 1234 0, 0123 0, 0012 0, 0001 6 Rząd liczby 2 to 1. Rząd liczby 3 to 1. 6 Rząd wielkości wyniku: 1+1– 1=1 rząd wielkości +3 +2 +1 0 -1 -2 -3

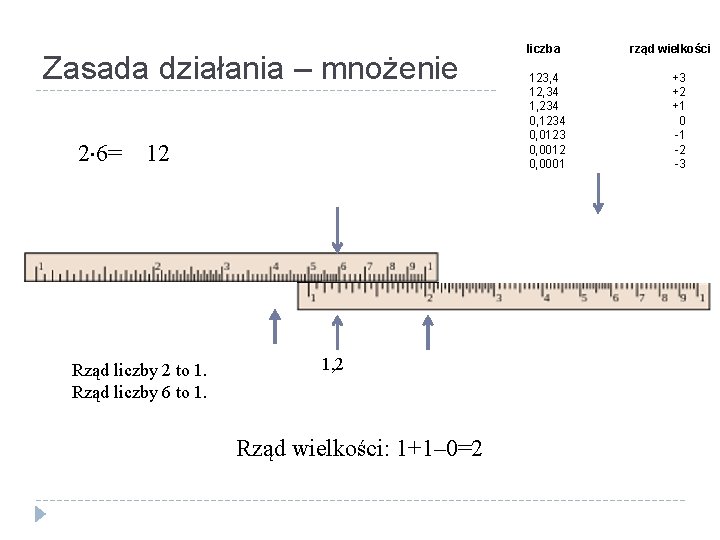
Zasada działania – mnożenie 2 6= 12 Rząd liczby 2 to 1. Rząd liczby 6 to 1. 1, 2 Rząd wielkości: 1+1– 0=2 liczba 123, 4 12, 34 1, 234 0, 1234 0, 0123 0, 0012 0, 0001 rząd wielkości +3 +2 +1 0 -1 -2 -3

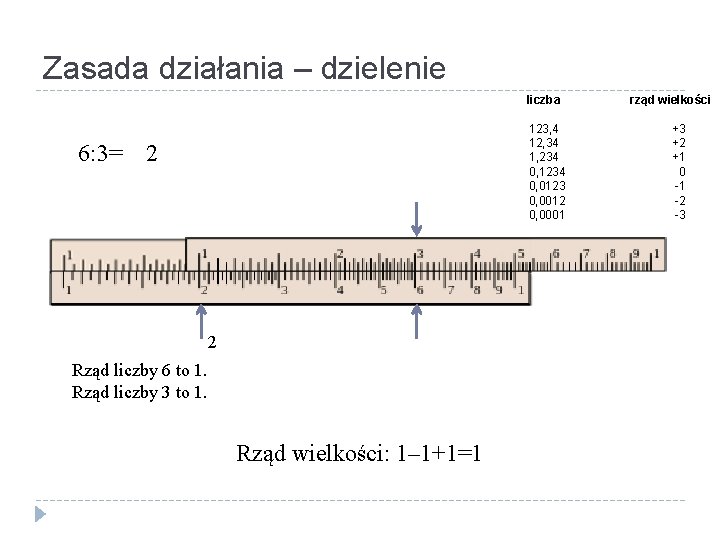
Zasada działania – dzielenie liczba 123, 4 12, 34 1, 234 0, 1234 0, 0123 0, 0012 0, 0001 6: 3= 2 2 Rząd liczby 6 to 1. Rząd liczby 3 to 1. Rząd wielkości: 1– 1+1=1 rząd wielkości +3 +2 +1 0 -1 -2 -3

Zasada działania – dzielenie liczba 123, 4 12, 34 1, 234 0, 1234 0, 0123 0, 0012 0, 0001 4: 8= 0, 5 Rząd liczby 4 to 1. Rząd liczby 8 to 1. 5 Rząd wielkości: 1– 1+0=0 rząd wielkości +3 +2 +1 0 -1 -2 -3

Podnoszenie do kwadratu Wybieramy liczbę na skali liczb naturalnych. Ustalamy rząd wielkości liczby, ozn. n. Odczytujemy wynik na skali kwadratów. Wynik na lewej połowie – rząd wielkości 2 n– 1. Wynik na prawej połowie – rząd wielkości 2 n.

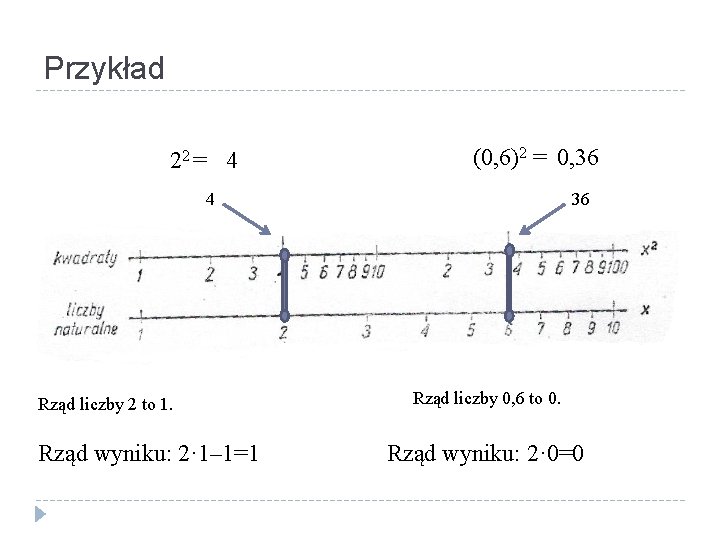
Przykład 22 = 4 (0, 6)2 = 0, 36 4 Rząd liczby 2 to 1. Rząd wyniku: 2· 1– 1=1 36 Rząd liczby 0, 6 to 0. Rząd wyniku: 2· 0=0

Podnoszenie liczby do trzeciej potęgi Wybieramy liczbę na skali liczb naturalnych. Ustalamy rząd wielkości liczby, ozn. n. Odczytujemy wynik na skali sześcianów. Wynik w lewej części – rząd wielkości 3 n– 2. Wynik w środkowej części – rząd wielkości 3 n– 1. Wynik w prawej części – rząd wielkości 3 n.

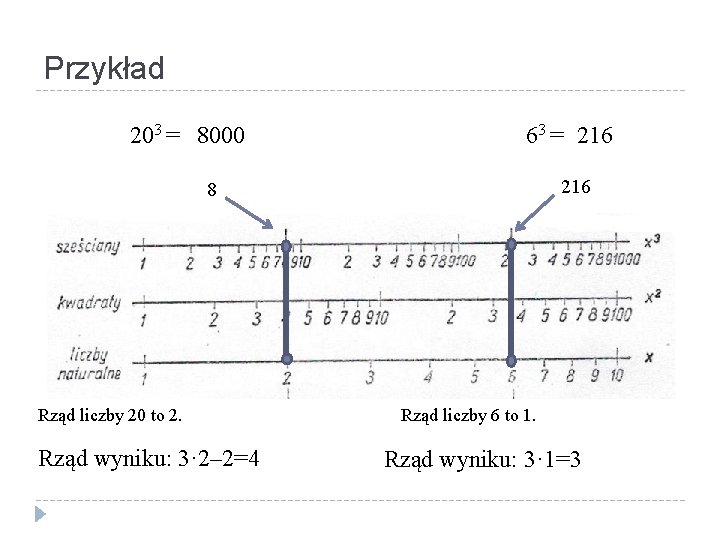
Przykład 203 = 8000 63 = 216 8 Rząd liczby 20 to 2. Rząd wyniku: 3· 2– 2=4 Rząd liczby 6 to 1. Rząd wyniku: 3· 1=3

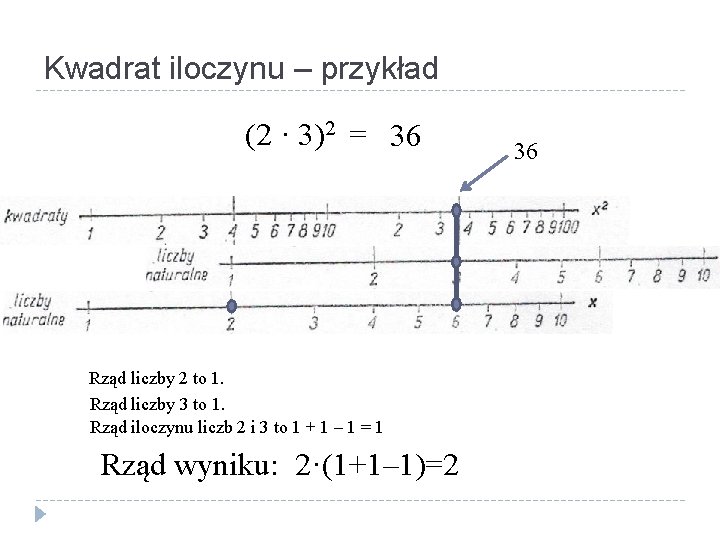
Kwadrat iloczynu – przykład (2 · 3)2 = 36 Rząd liczby 2 to 1. Rząd liczby 3 to 1. Rząd iloczynu liczb 2 i 3 to 1 + 1 – 1 = 1 Rząd wyniku: 2·(1+1– 1)=2 36

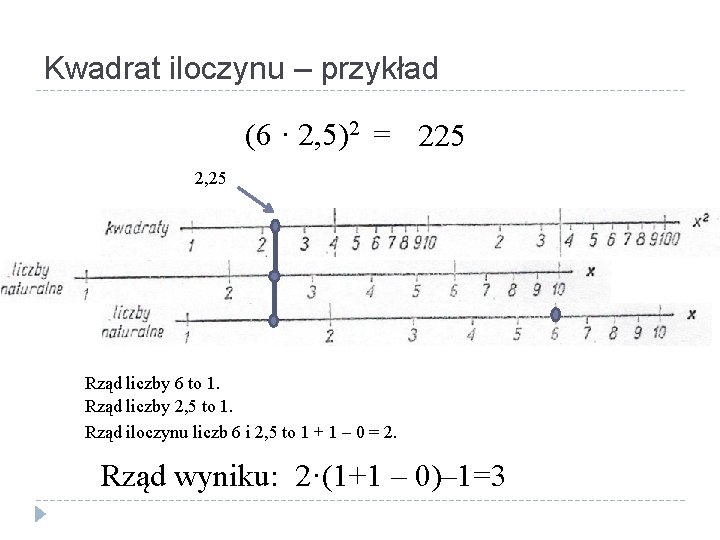
Kwadrat iloczynu – przykład (6 · 2, 5)2 = 225 2, 25 Rząd liczby 6 to 1. Rząd liczby 2, 5 to 1. Rząd iloczynu liczb 6 i 2, 5 to 1 + 1 – 0 = 2. Rząd wyniku: 2·(1+1 – 0)– 1=3

Dokładność obliczeń suwaka Przeciętny użytkownik potrafi rozróżnić na podziałce odległość 0, 25 mm. Najpowszechniejszy suwak ma długość 25 cm. Błąd odczytu wynosi To stanowi 0, 1% odczytywanej liczby.

Typy suwaków – suwaki walcowe Suwak logarytmiczny Motorola Universal Circle Slide Rule Suwak logarytmiczny Loga Calculator

Typy suwaków – suwaki cylindryczne Suwak logarytmiczny Otis King Calculator

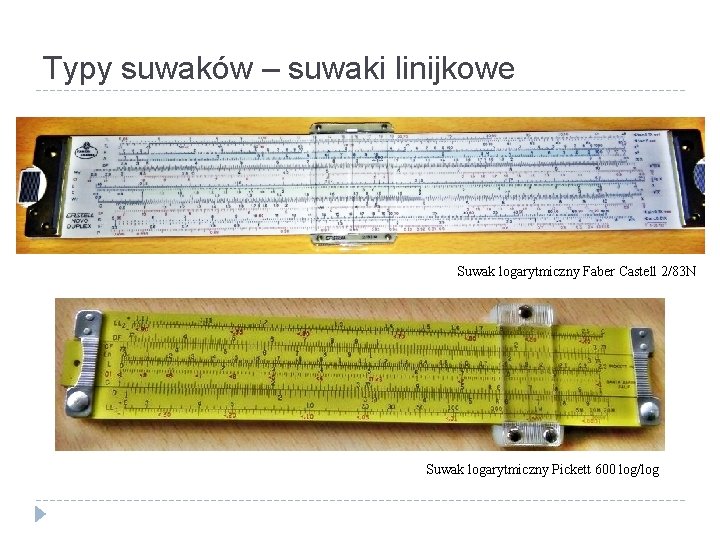
Typy suwaków – suwaki linijkowe Suwak logarytmiczny Faber Castell 2/83 N Suwak logarytmiczny Pickett 600 log/log

Typy suwaków – suwaki kołowe Suwak logarytmiczny Fowler’s „Magnum” Suwak logarytmiczny KL-1 Slide Rule

Typy suwaków – suwaki specjalistyczne Suwak Fowler’s Textile Calculator

Typy suwaków – suwaki specjalistyczne Suwak Safetech E 6 -B Flight Computer

Typy suwaków – suwaki specjalistyczne Przyrząd do wstrzeliwania wz. 1987

Typy suwaków – suwaki specjalistyczne Suwak Fraction-of-an-inch Adding Machine

Typy suwaków – suwaki specjalistyczne Suwak dozymetryczny Skala

Podziękowania Dziękujemy p. Maciejowi Syśle p. Małgorzacie Mikołajczyk za udostępnienie modeli suwaków logarytmicznych. Dziękujemy za uwagę!

Bibliografia • Bondecka-Krzykowska I. , Historia obliczeń. Od rachunku na palcach do maszyny analitycznej, Poznań 2013, str. 161 – 172. • Chmielewski H. , Logarytmiczny suwak rachunkowy, Warszawa 1963. • https: //pl. wikipedia. org/wiki/Suwak_logarytmiczny • http: //www. sawicki. cc/Suwak%20 logarytmiczny. htm • https: //pl. wikipedia. org/wiki/John_Napier • https: //pl. wikipedia. org/wiki/William_Oughtred • http: //www. animations. physics. unsw. edu. au/jw/d. B. htm • http: //www. tomek. strony. ug. edu. pl/suwak_log. pdf