Sustainable Resource Engineering Course Note 1 1 Reaction

Sustainable Resource Engineering Course Note 1 -1 (Reaction Principles) Joonhong Park Yonsei CEE Department 2015. 9. 14. CEE 3330 Y 2013 WEEK 3

Contents: 1. Dynamics of Transformation Processes - stoichiometry - thermodynamics - kinetics CEE 3330 Y 2013 WEEK 3

Intro: Governing Concepts of Transformation Processes - Stoichiometry: how much can you get? - Thermodynamics: can the reaction occur? - Kinetics: how fast? a. A +b. B c. C + d. D Ex. CH 4 + 2 O 2 = 1 CO 2 + 2 H 2 O CEE 3330 Y 2013 WEEK 3

Stoichiometry The application of the principle of material balance to a chemical transformation. b. R 1 + c. R 2 => m. P 1 + n. P 2 here R 1 and R 2: reactants P 1 and P 2: products b, c, m, and n: stoichiometric coefficients Meaning: b molecules of R 1 combine with c molecules of R 2 to form m molecules of P 1 and n molecules of P 2 RULE: A chemical reaction must conserve (i) the number of atoms for each element involved in the reaction and (ii) the electrical charge associated with ions. CEE 3330 Y 2013 WEEK 3

Stoichiometry Example: A general photosynthesis reaction my be written in the form shown below. Use the principle of stoichiometry to determine the coefficients a-f. a. CO 2 + b. NO 3 - + c. HPO 42 - + d. H+ + e. H 2 O => C 106 H 263 O 110 N 16 P 1+ f. O 2 C: a =106 O: 2 a + 3 b + 4 c + e = 110 + 2 f N: b=16 H: c + d + 2 e = 263 P: c =1 +/-: -b -2 c + d = 0 a=106 b=16 c=1 d= b + 2 c = 16 + 2 = 18 e = 0. 5*(263 -c–d) =122 f=0. 5*(110 -2 a-3 b-4 c-e)=138 CEE 3330 Y 2013 WEEK 3

Stoichiometry Example: Benzene (C 6 H 6) can be oxidized in the presence of oxygen. The complete oxidization of benzene produces CO 2 and H 2 O. Calculate how many moles of oxygen molecules have to be needed for one mole of benzene to be completely oxidized. C 6 H 6 + a. O 2 => m. CO 2 + n. H 2 O Since # of C should be 6 in the left-hand term, m =6. (MB for C atoms) Since # of H should be 6 in the left-hand term, n=3. (MB for H atoms) Therefore, total # of O in the right-hand term is 6*2 + 3*1 = 15. And a should be 15/2 (MB for O atoms) CEE 3330 Y 2013 WEEK 3

Chemical Energy (Gibbs Free Energy, G) Enthalpy, H = U + W (M L 2 T-2) U: internal energy W: external energy (W = PV; 압력 X 부피) endothermic (흡열반은, d. H > 0) exothermic (발열반응, d. H < 0) H = G +TS (M L 2 T-2) G: Gibbs Free Chemical Energy TS: Entropy Gain Function (T = absolute temp. ; S = entropy) CEE 3330 Y 2013 WEEK 3

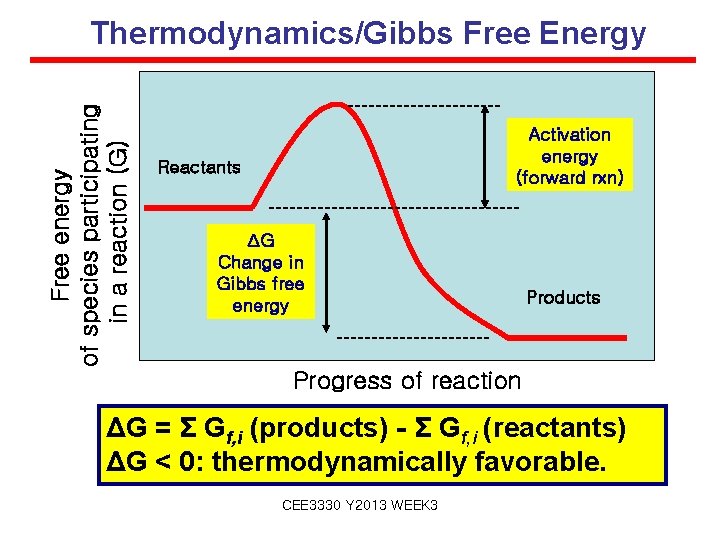
Free energy of species participating in a reaction (G) Thermodynamics/Gibbs Free Energy Activation energy (forward rxn) Reactants ΔG Change in Gibbs free energy Products Progress of reaction ΔG = Σ Gf, i (products) - Σ Gf, i (reactants) ΔG < 0: thermodynamically favorable. CEE 3330 Y 2013 WEEK 3

Thermodynamics/Gibbs Free Energy ΔG = Σ Gf, i (products) - Σ Gf, i (reactants) Gf, i = ni [Gof, i + RT ln {i}] n: # of moles of species i. {i}: activity of species i. (when diluted, {i} = [i]) Gof, i : Gibbs free energy for species i at reference conditions (T=298 K, P =1 atm) 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Thermodynamics/Gibbs Free Energy Example: Using free energy to determine the direction of a reaction. Water that is in contact with solid lime (Ca(OH)2) at 25 o. C contains concentrations of calcium and hydroxide ions of 10 -5 M and 10 -4 M, respectively. Given: Gof for Ca(OH)2 = -898. 4 k. J/mol; Gof for Ca 2+ = -553. 1 k. J/mol; Gof for OH- = -157. 3 k. J/mol) Ca(OH)2 (s) Ca 2+ + 2 OHSolution) Ca(OH)2: Gf, = 1*[-898. 4 k. J/mol + RT ln[Ca(OH)2] = -898. 4 k. J/mol Ca 2+: Gf = 1*[-553. 1 k. J/mol + RT ln[Ca 2+]] = -582. 1 k. J/mol OH-: Gf = 2 * [-157. 3 k. J/mol + RT ln[OH-]] = -360. 2 k. J/mol ΔG = Σ G f, i (products) - Σ G f, i (reactants) = (-582. 1 -360. 2) – (- 898. 4) = - 43. 9 k. J/mol < 0 Forward direction! CEE 3330 Y 2013 WEEK 3

Thermodynamics/Gibbs Free Energy a. A + b. B c. C + d. D ( at a given temperature, T) ΔG = Σ Gf, i (products) - Σ Gf, i (reactants) Gf, A = a [Gof, A + RT ln {A}] Gf, B = b [Gof, B + RT ln {B}] Gf, C = c [Gof, C + RT ln {C}] Gf, D = d [Gof, D + RT ln {D}] ΔG = -a*Gof, A - b*Gof, B + c*Gof, C + d*Gof, D + RT ln[{A}-a{B}-b{C}+c{D}+d] o + RT ln. Q = ΔG Environmental Chemical properties 2022 -02 -13 factors (온도, 농도) CEE 3330 Joonhong Park Copy Right

Chemical Equilibrium/Thermodynamics When a system is at “chemical equilibrium”, the distribution of elements among chemical species and the distribution of species among physical states (phases) satisfies thermodynamic relationships, regardless of the history of the system. A system at chemical equilibrium must satisfy: 1. It does not vary with time. 2. It is internally uniform (at least at the level of discrete subsystems). 3. There are not net flows of mass, heat, or species within the system or between the systems and its surroundings. 4. The net rate of all chemical reactions is zero. The net rate of a reaction is the difference between the rates of the forward and reverse reactions. CEE 3330 Y 2013 WEEK 3

Chemical Equilibrium/Thermodynamics a. A + b. B c. C + d. D ( at a given temperature, T) ΔG = 0 = Σ Gf, i (products) - Σ Gf, i (reactants) Gf, A = a [Gof, A + RT ln {A}] Gf, B = b [Gof, B + RT ln {B}] Gf, C = c [Gof, C + RT ln {C}] Gf, D = d [Gof, D + RT ln {D}] 0 = -a*Gof, A - b*Gof, B + c*Gof, C + d*Gof, D + RT ln[{A}-a{B}-b{C}+c{D}+d] = ΔGo + RT ln. K here, Equilibrium Constant, K = Exp [-ΔGo /RT] 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Thermodynamics/Gibbs Free Energy Example: CNO- + 2 H 3 O+ NH 4+ + H 2 CO 3 (1) Calculate K value Given: Gof for CNO- = -98. 7 k. J/mol; Gof for H 3 O+ = -237. 2 k. J/mol; Gof for NH 4+ = -79. 5 k. J/mol; Gof for H 2 CO 3 = -623. 4 k. J/mol) (R=8. 314 J/mol/K; RT ln K = 5. 7 log 10 K when unit is k. J/mol) (2) Calculate p. H when [CNO-]=10 -8 M and [NH 4+]=[H 2 CO 3]= 1 M 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Kinetics a. A + b. B => c. C + d. D ( at a given temperature, T) (intrinsic) Reaction Rate Rf = - (1/a) (d[A]/dt) = -(1/b)(d[B]/dt) = (1/c)(d[C]/dt) = (1/d)(d[D]/dt) In general, Rf ∝ - ΔG or f (ΔG) Rate Laws Rf = kf [A]α[B]β here kf = rate constant α = reaction order with respect with [A] β = reaction order with respect with [B] CEE 3330 Y 2013 WEEK 3

Elementary versus Non-elementary Reactions Elementary Reaction orders correspond to the stoichiometric coefficients Non-elementary Reaction 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Reaction Order • The order of reaction refers the powers to which the concentrations are raised in the kinetic rate law. • The reaction is α order with respect to reactant A, and β order with respect to reactant B. • The overall order is n (= α + β ). CEE 3330 Y 2013 WEEK 3

Reaction Order (II): Unit of Rate Constant Oth order {k} = mol/L/sec 1 st order {k} = 1/sec 2 nd order {k} = L/mol/sec 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Empirical Determination of Reaction Order and Rate Constant (I) Oth order [A] = Ao -kt 1 st order [A] = Ao Exp[-kt] Ln[A] =Ln. Ao -kt [A] = Ao /(1 + kt. Ao) 1/[A] =Ln. Ao -kt 2 nd order Differential 2022 -02 -13 Integrated CEE 3330 Joonhong Park Copy Right Linearlized

Kinetics Example: solving a simple kinetic problem Radon-222 => polonium-218 + alpha particle (elementary reaction) The rate constant for this rxn is k = 2. 1 x 10 -6 s-1, independent of temperature. At t=0, a batch reactor is filled with air containing radon at concentration Co. How does the radon concentration in the reactor change over time? Solution) R = - d. CRn-222/dt = k. CRn-222 d. CRn-222/CRn-222 = - k dt ln. CRn-222 - ln. Co = -k (t – 0) => CRn-222 = Co Exp(-kt) 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Rate Constants and Equilibrium Constant (I) Example: Reversible element rxn. 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Rate Constants and Equilibrium Constant (II) Where Kf = equilibrium constant on a basis of the forward rxn. 2022 -02 -13 CEE 3330 Joonhong Park Copy Right

Summary I: Dynamics of Transformation Processes Stoichiometry: a. A +b. B = c. C + d. D => Predicting the equilibrium concentrations of reactants and products of a reaction Thermodynamics: ΔG <0 ? or Q vs. K ÞPredicting the direction of a reaction ÞComparing the feasibility of candidate reactions Kinetics: Rf = kf [A]α[B]β => Predicting the reaction rate of a reactor, and being useful in calculating non-equilibrium concentrations in a system CEE 3330 Y 2013 WEEK 3

Summary II: System and Process Dynamics • System and Process Identification a. A + b. B c. C + d. D ( at T) • System Dynamics: Material/Mass Balance Accumulation rate = Input rate – Output rate + Reaction rate • Transformation Process Dynamics - Chemical species - Reaction and Stoichiometry - Thermodynamics - Kinetics (Reaction rate) CEE 3330 Y 2013 WEEK 3