Surveying Prospection for Archaeology Environmental Science Topographic Surveying

Surveying & Prospection for Archaeology & Environmental Science Topographic Surveying & Feature Mapping Phil Buckland

Contents • Topographic survey & feature mapping • Equipment - introduction • Coordinates & Trigonometry - the basic maths of triangles • Surveying in practice • Alternative data acquisition (briefly)

Topographic survey & feature mapping Topographic survey - create a cartographic representation of landscape features - coordinate data (x, y, z - or variants of) - detail (scale/resolution) defined by project aims - end product usually a 2 D contour map (but 3 D models becoming more common) - field techniques improve realism/accuracy

Topographic survey & feature mapping Feature mapping (objects) - site specific, many variations - locate & relate objects/areas spatially - includes attribute data on objects (object type, name etc. ) as well as coordinates. This is a key feature of GIS - end product often a 2 D map or 3 D model - can overlay on topographic maps

Equipment - introduction Three groups used (in this course): - Levels (dumpy level, theodolite) - Total Stations (EDM - Electronic Distance Measurers) - GPS (Global Positioning System)

Equipment - introduction

Coordinates Relate points/objects together in space - in a plane (horizontal) - vertically (height) Using coordinates (e. g. x, y, z) with the help of angles and distances Bearing = angle relative to reference direction (e. g. North, grid North. . . )

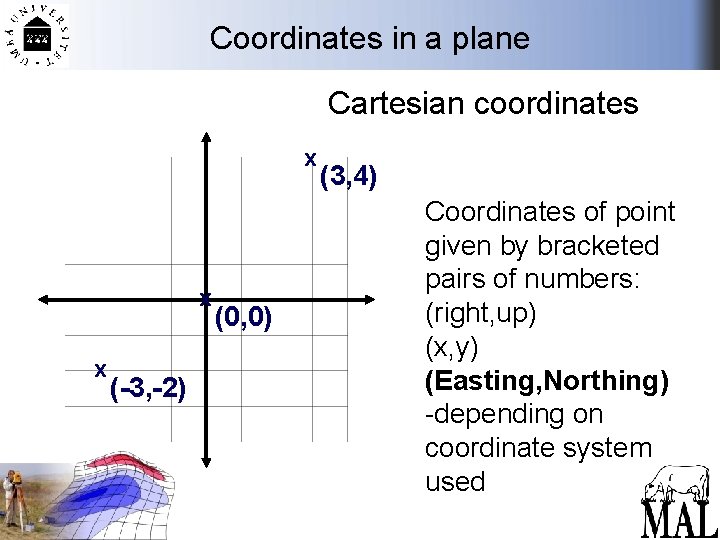
Coordinates in a plane Cartesian coordinates + - x - (0, 0) Perpendicular axes Origin at (0, 0) Coordinates increase right & up of origin + Coordinates decrease down & left of origin Descarte (1637)

Coordinates in a plane Cartesian coordinates x x x (-3, -2) (0, 0) (3, 4) Coordinates of point given by bracketed pairs of numbers: (right, up) (x, y) (Easting, Northing) -depending on coordinate system used

Coordinates in a plane Often easier to avoid negative values by x (1004, 1006) increasing origin coordinates + x x (1001, 1002) (1000, 1000) x (998, 999) + NOTE: Some countries (incl. Sweden) use on maps: y=East x=North Others use opposite (e. g. (England, USA) We’ll use (Easting, Northing)

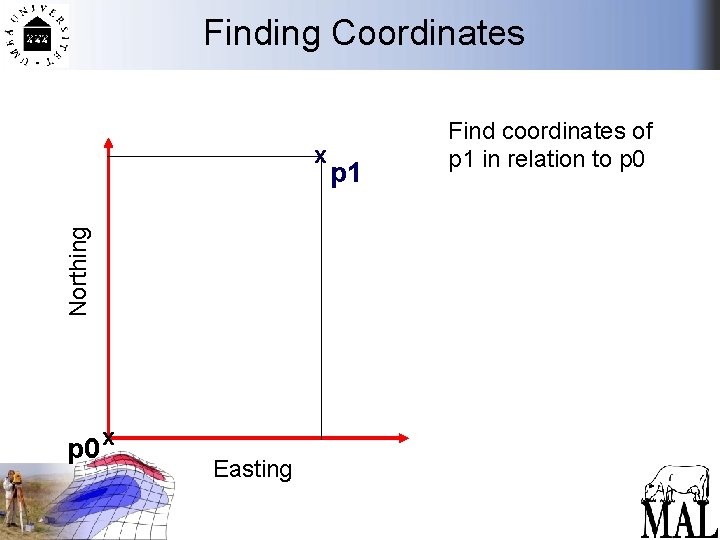
Finding Coordinates Northing x p 0 x Easting p 1 Find coordinates of p 1 in relation to p 0

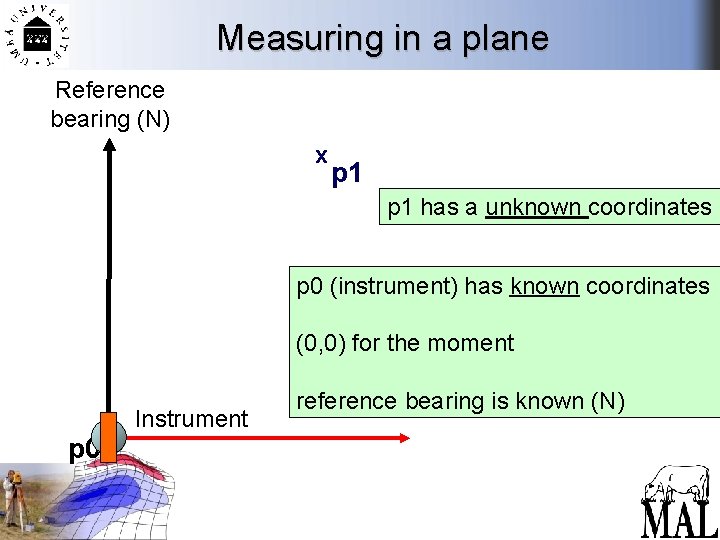
Measuring in a plane Reference bearing (N) x p 1 has a unknown coordinates p 0 (instrument) has known coordinates (0, 0) for the moment p 0 x Instrument reference bearing is known (N)

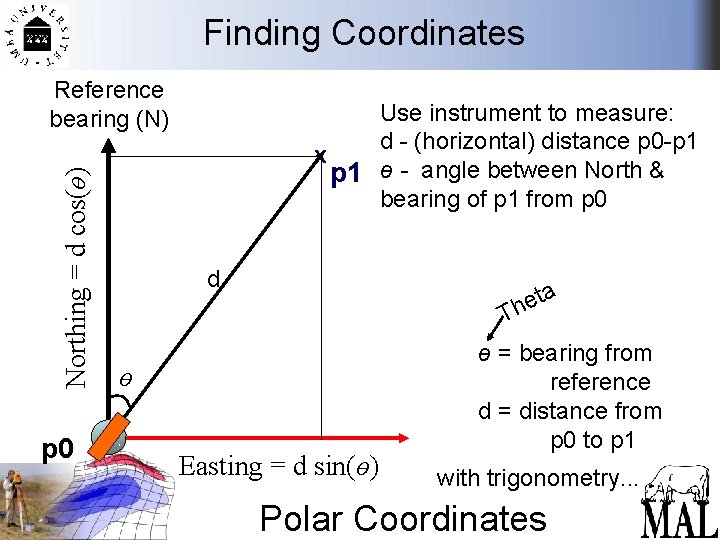
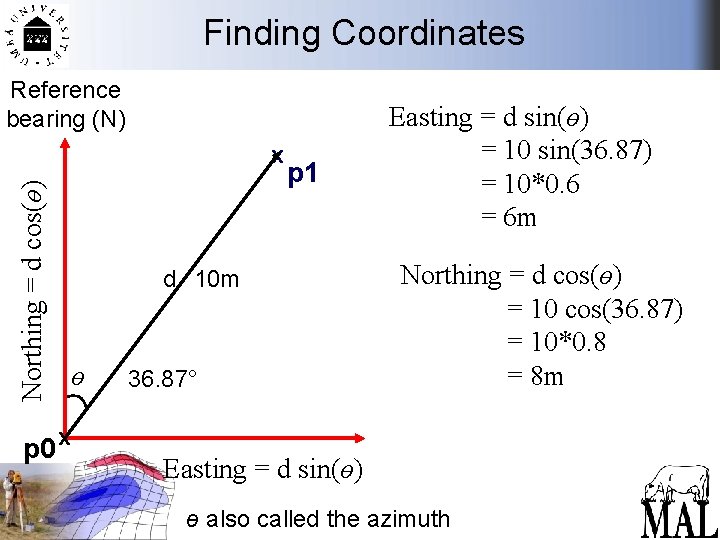
Finding Coordinates Northing = d cos(ө) Reference bearing (N) p 0 Use instrument to measure: d - (horizontal) distance p 0 -p 1 x p 1 ө - angle between North & bearing of p 1 from p 0 d ta e Th ө Easting = d sin(ө) ө = bearing from reference d = distance from p 0 to p 1 with trigonometry. . . Polar Coordinates

Finding Coordinates Reference bearing (N) Northing = d cos(ө) x p 1 d 10 m ө p 0 x 36. 87° Easting = d sin(ө) = 10 sin(36. 87) = 10*0. 6 = 6 m Northing = d cos(ө) = 10 cos(36. 87) = 10*0. 8 = 8 m Easting = d sin(ө) ө also called the azimuth

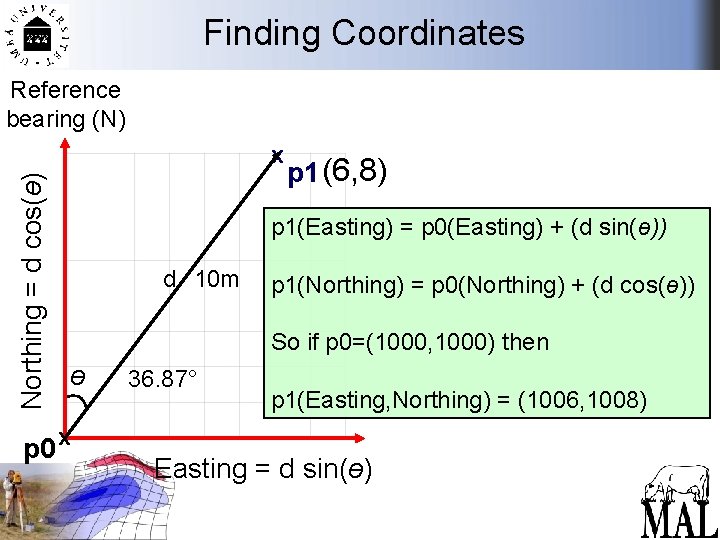
Finding Coordinates Reference bearing (N) Northing = d cos(ө) x p 1 (6, 8) p 1(Easting) = p 0(Easting) + (d sin(ө)) d 10 m p 1(Northing) = p 0(Northing) + (d cos(ө)) So if p 0=(1000, 1000) then ө p 0 x 36. 87° p 1(Easting, Northing) = (1006, 1008) Easting = d sin(ө)

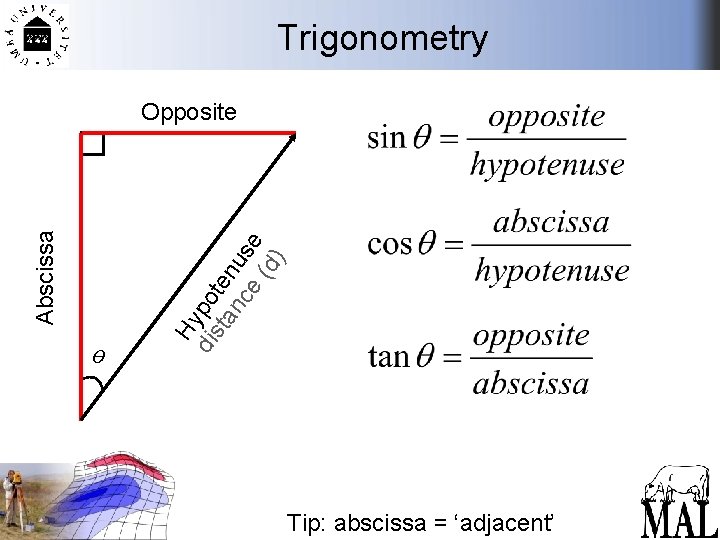
Trigonometry ө Hy dis po ta ten nc us e e (d ) Abscissa Opposite Tip: abscissa = ‘adjacent’

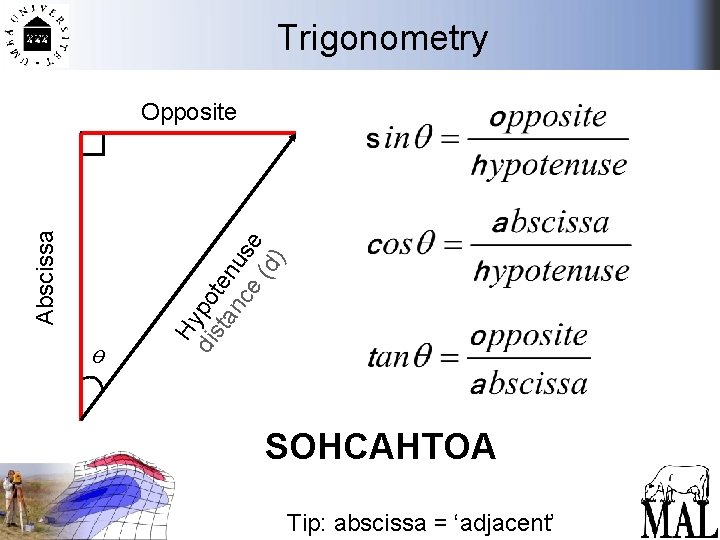
Trigonometry ө Hy dis po ta ten nc us e e (d ) Abscissa Opposite SOHCAHTOA Tip: abscissa = ‘adjacent’

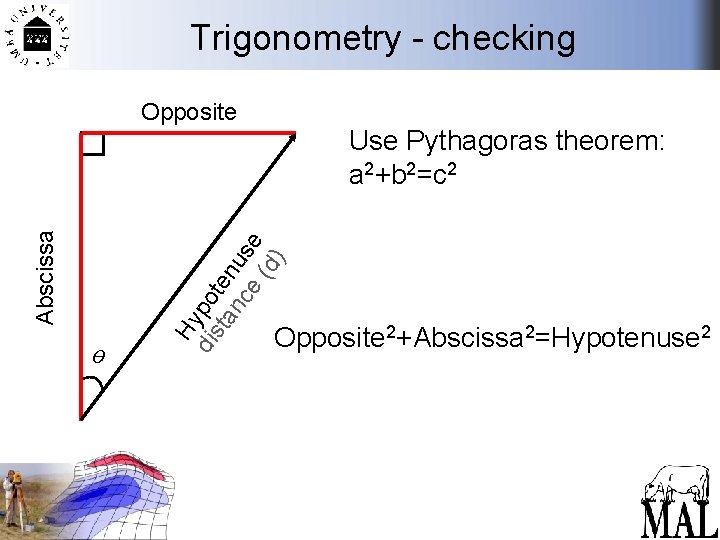
Trigonometry - checking ө Use Pythagoras theorem: a 2+b 2=c 2 Hy dis po ta ten nc us e e (d ) Abscissa Opposite 2+Abscissa 2=Hypotenuse 2

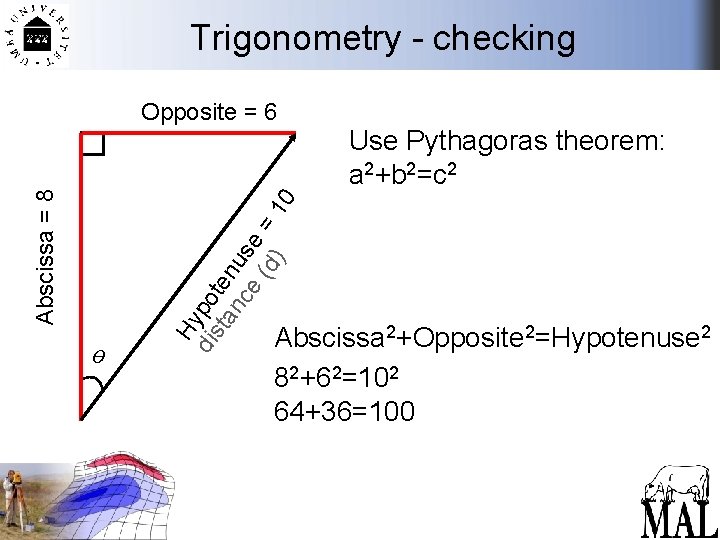
Trigonometry - checking ө Hy dis po ta ten nc us e e (d = 10 ) Abscissa = 8 Opposite = 6 Use Pythagoras theorem: a 2+b 2=c 2 Abscissa 2+Opposite 2=Hypotenuse 2 82+62=102 64+36=100

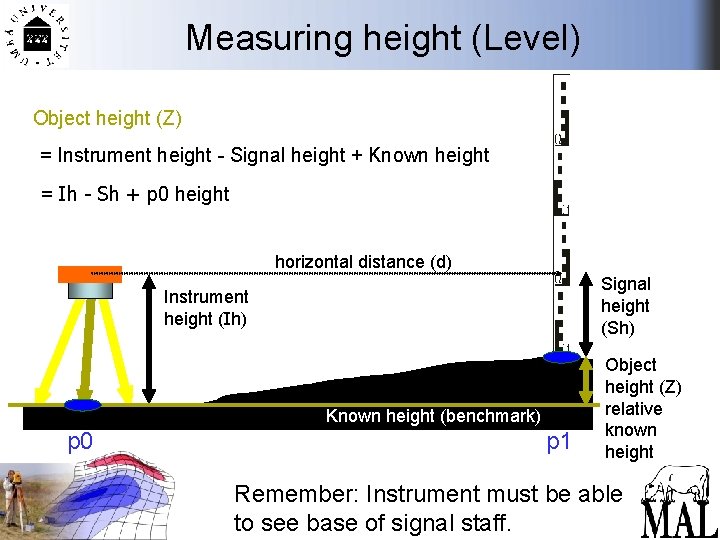
Measuring height (Level) Object height (Z) = Instrument height - Signal height + Known height = Ih - Sh + p 0 height horizontal distance (d) Signal height (Sh) Instrument height (Ih) Objekt Known height (benchmark) p 0 p 1 Object height (Z) relative known height Remember: Instrument must be able to see base of signal staff.

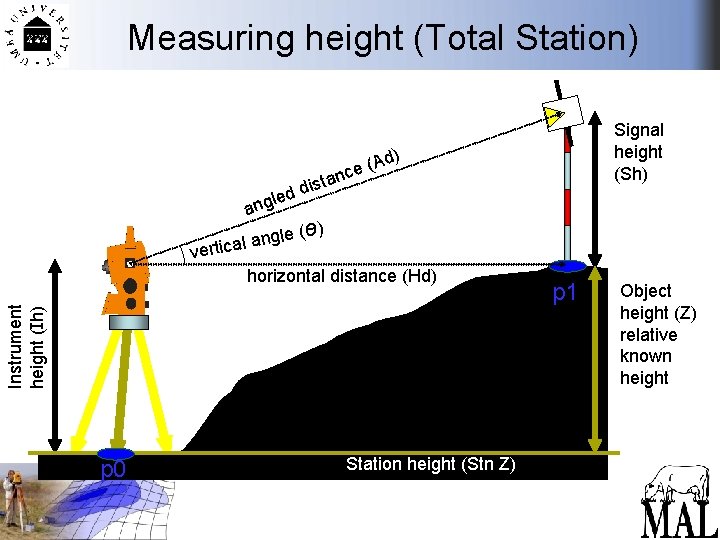
Measuring height (Total Station) Signal height (Sh) d) st i d ed l ang gle (ө n a l a rtic (A nce a ) ve Instrument height (Ih) horizontal distance (Hd) p 0 Station height (Stn Z) p 1 Object height (Z) relative known height

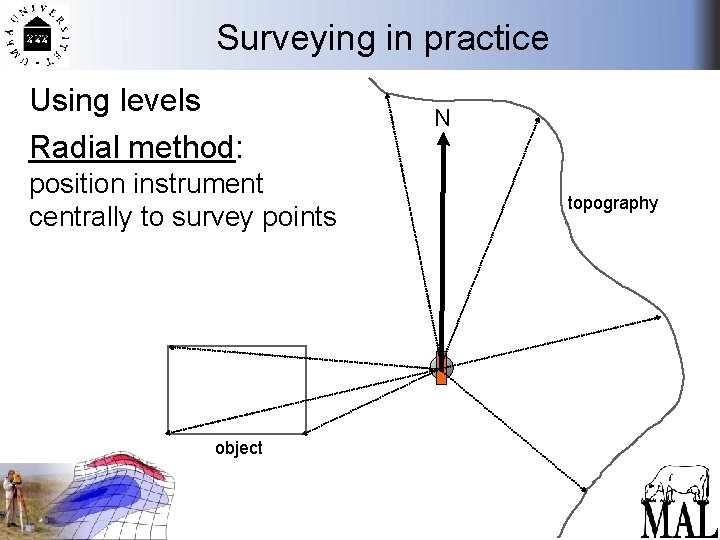
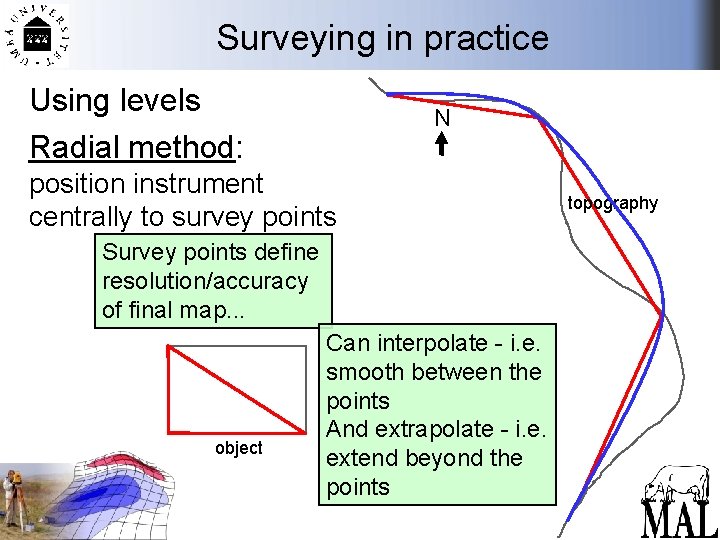
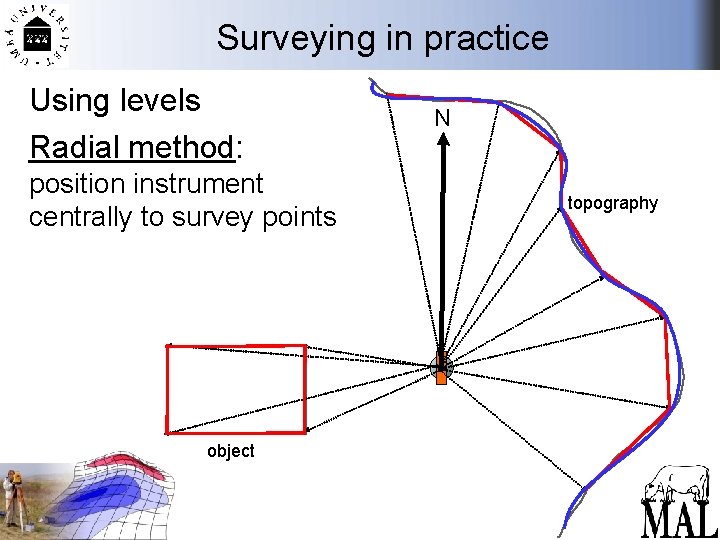
Surveying in practice Using levels Radial method: position instrument centrally to survey points object N topography

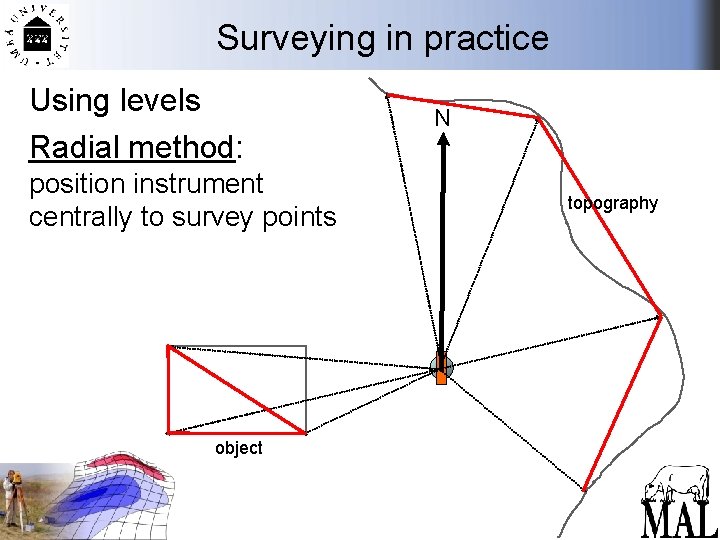
Surveying in practice Using levels Radial method: position instrument centrally to survey points object N topography

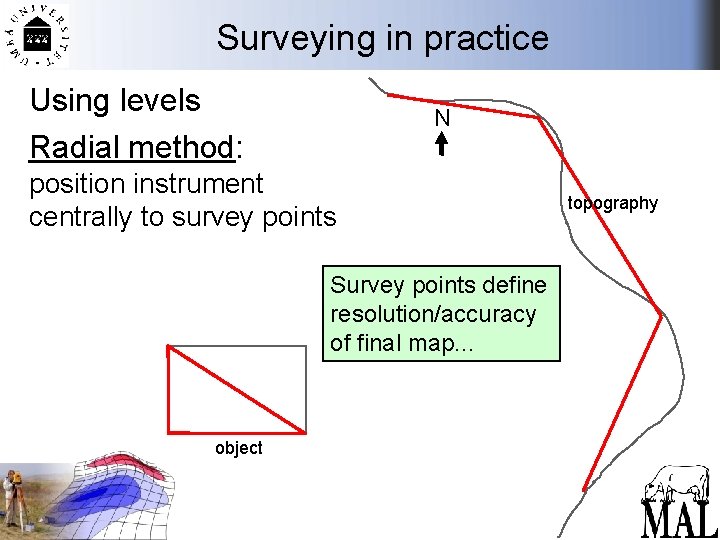
Surveying in practice Using levels Radial method: N position instrument centrally to survey points Survey points define resolution/accuracy of final map. . . object topography

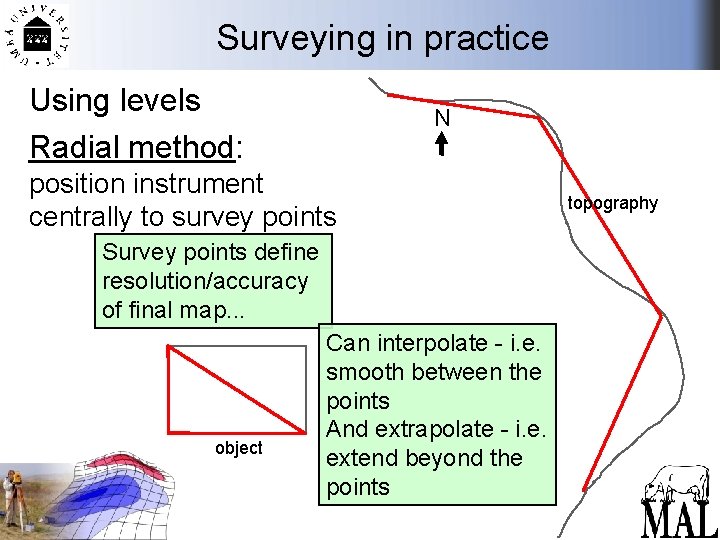
Surveying in practice Using levels Radial method: N position instrument centrally to survey points Survey points define resolution/accuracy of final map. . . object Can interpolate - i. e. smooth between the points And extrapolate - i. e. extend beyond the points topography

Surveying in practice Using levels Radial method: N position instrument centrally to survey points Survey points define resolution/accuracy of final map. . . object Can interpolate - i. e. smooth between the points And extrapolate - i. e. extend beyond the points topography

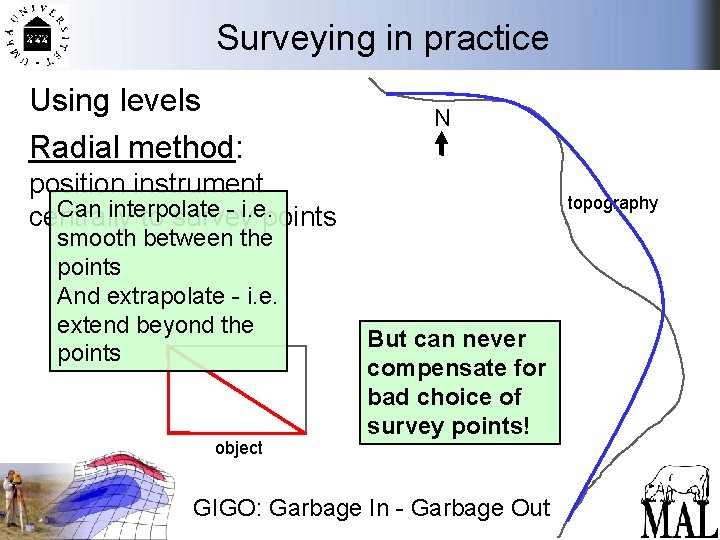
Surveying in practice Using levels Radial method: N position instrument Can interpolate - i. e. points centrally to survey smooth between the points And extrapolate - i. e. extend beyond the points object topography But can never compensate for bad choice of survey points! GIGO: Garbage In - Garbage Out

Surveying in practice Using levels Radial method: position instrument centrally to survey points object N topography

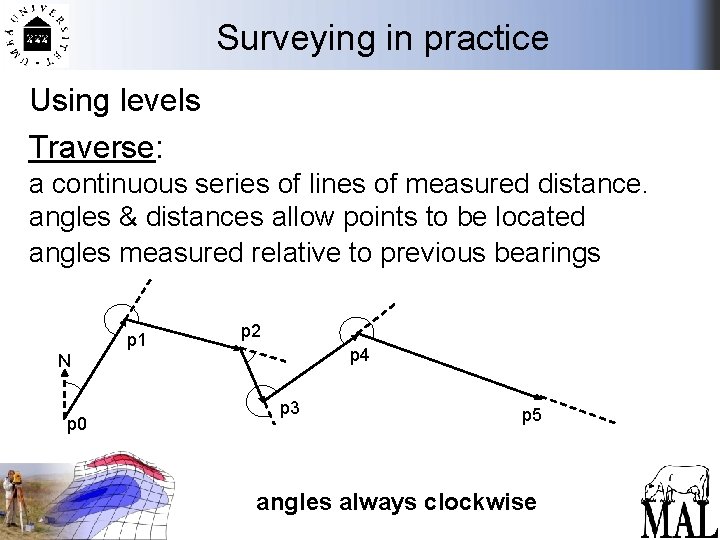
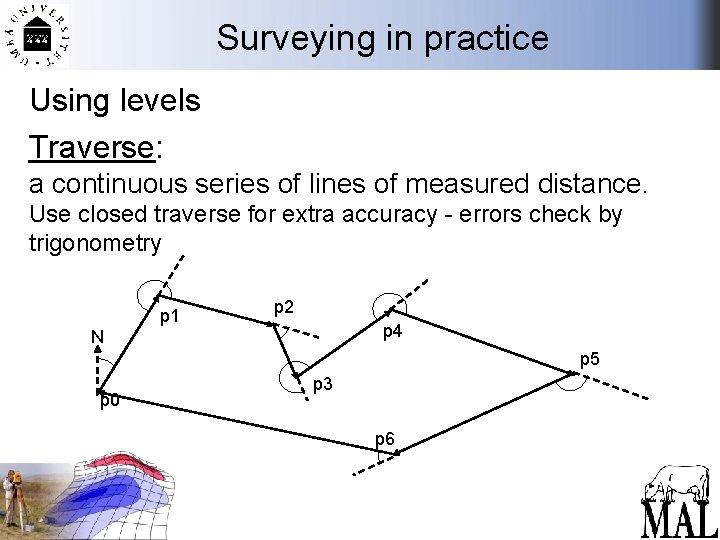
Surveying in practice Using levels Traverse: a continuous series of lines of measured distance. angles & distances allow points to be located angles measured relative to previous bearings p 1 p 2 p 4 N p 0 p 3 p 5 angles always clockwise

Surveying in practice Using levels Traverse: a continuous series of lines of measured distance. Use closed traverse for extra accuracy - errors check by trigonometry p 1 p 2 p 4 N p 5 p 0 p 3 p 6

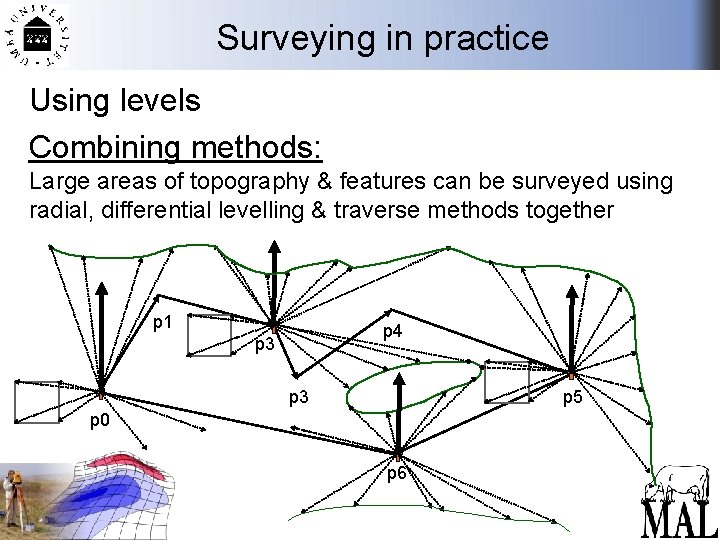
Surveying in practice Using levels Combining methods: Large areas of topography & features can be surveyed using radial, differential levelling & traverse methods together p 1 p 4 p 3 p 5 p 3 p 0 p 6

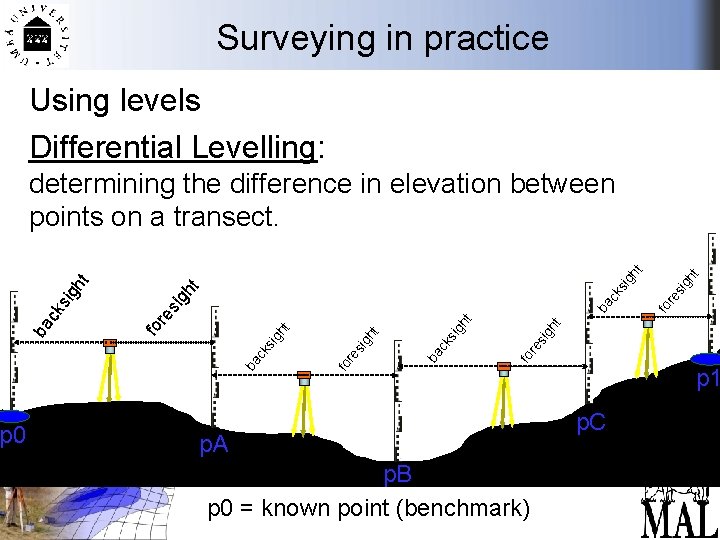
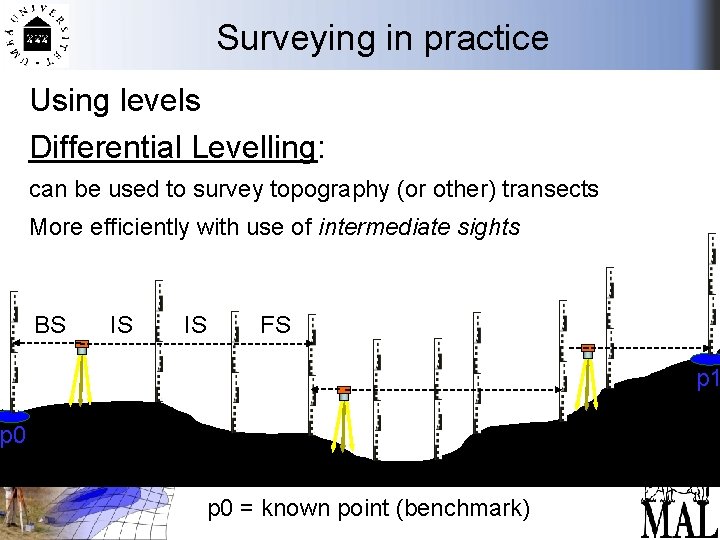
Surveying in practice Using levels Differential Levelling: p 0 sig ht re fo ba ck re sig ht fo sig ht ba ck sig ht re fo ba ck sig ht determining the difference in elevation between points on a transect. p. A p. B p 0 = known point (benchmark) p 1 p. C

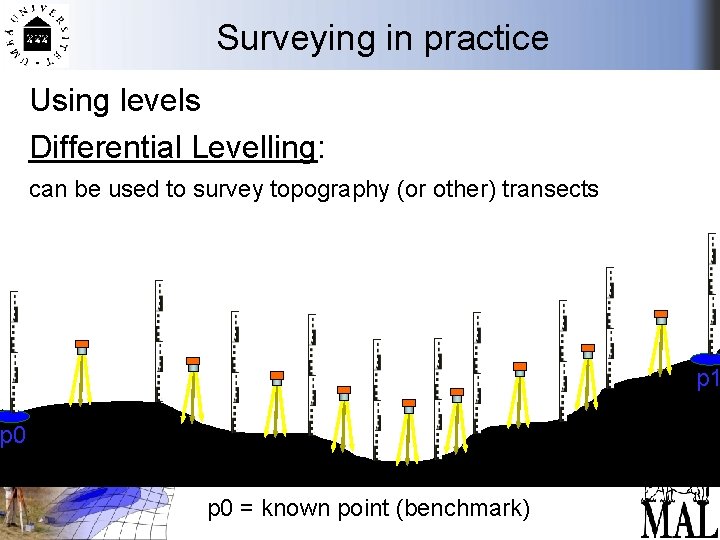
Surveying in practice Using levels Differential Levelling: can be used to survey topography (or other) transects p 1 p 0 = known point (benchmark)

Surveying in practice Using levels Differential Levelling: can be used to survey topography (or other) transects More efficiently with use of intermediate sights BS IS IS FS p 1 p 0 = known point (benchmark)

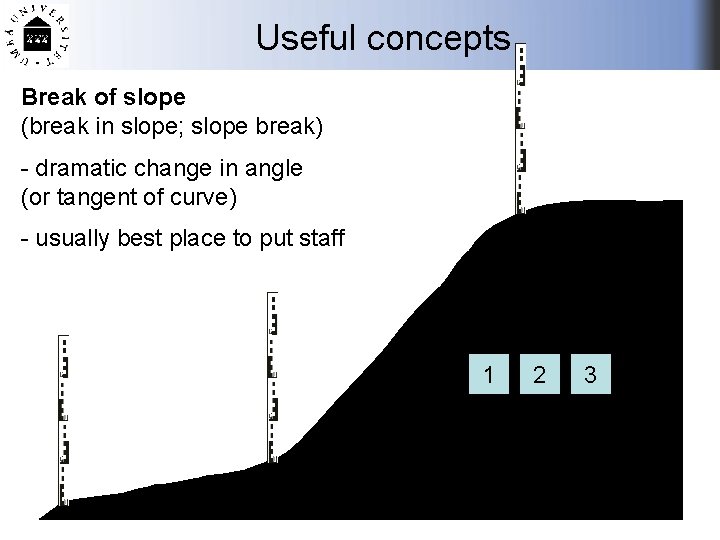
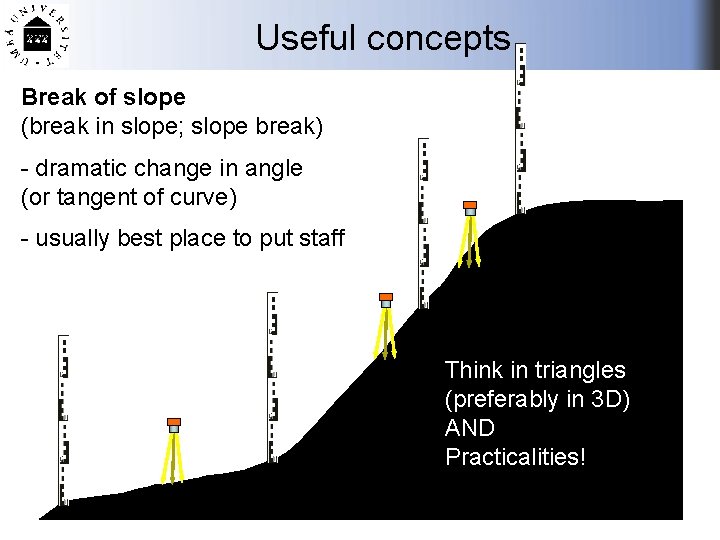
Useful concepts Break of slope (break in slope; slope break) - dramatic change in angle (or tangent of curve) - usually best place to put staff 1 2 3

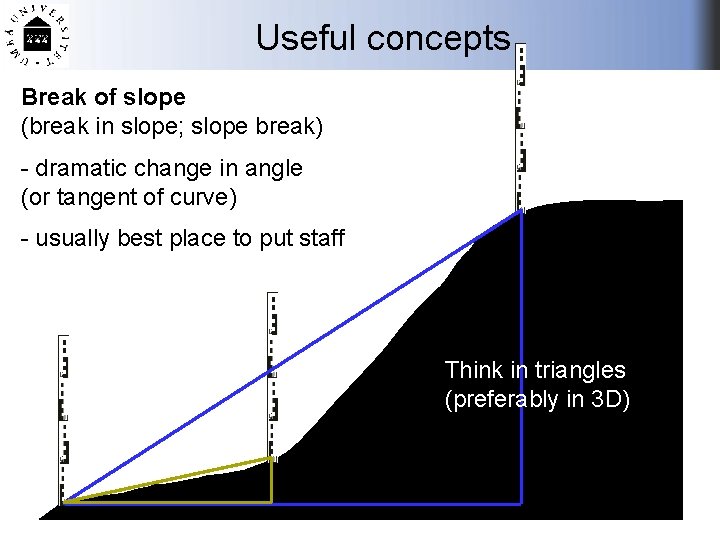
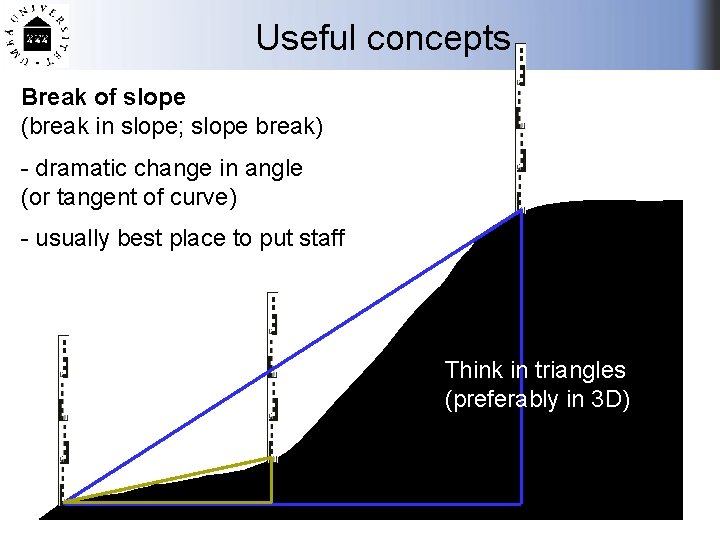
Useful concepts Break of slope (break in slope; slope break) - dramatic change in angle (or tangent of curve) - usually best place to put staff Think in triangles (preferably in 3 D)

Useful concepts Break of slope (break in slope; slope break) - dramatic change in angle (or tangent of curve) - usually best place to put staff Think in triangles (preferably in 3 D)

Useful concepts Break of slope (break in slope; slope break) - dramatic change in angle (or tangent of curve) - usually best place to put staff Think in triangles (preferably in 3 D) AND Practicalities!

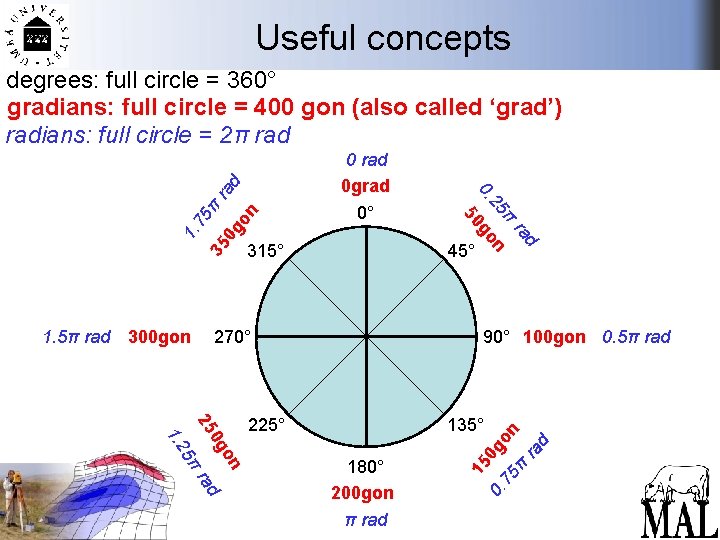
Useful concepts Different angle measurements degrees: trigonometry, common usage full circle = 360° gradians: surveying, engineering full circle = 400 gon (or grad) radians: mathematics, physics, Excel full circle = 2π rad

Useful concepts d ra π n go 45° 315° 270° 90° 100 gon 0. 5π rad 135° n go π d ra 180° 200 gon π rad 0. 0 go 75 π n ra d 0 25 5 1. 2 225° 15 1. 5π rad 300 gon 25 0° 0. 0 rad 0 grad 50 1. 75 π 35 0 g rad on degrees: full circle = 360° gradians: full circle = 400 gon (also called ‘grad’) radians: full circle = 2π rad

Useful concepts Conversion between angle measures: use DRG► (or DEG etc) button on calculator gon to degrees: gon to radians:

Useful concepts Conversion between angle measures: Excel uses radians in formulae (e. g. =sin(), =cos(), =tan()) In Excel: degrees to radians: =RADIANS(angle_in_degrees) gon to radians: =RADIANS(angle_in_gon/400*360)

Alternative data acquisition Aerial photographs Orthophotos - geometrically corrected aerial photographs GPS surveying - varying degrees of accuracy Satellite data - elevation; infra-red etc. ; with image analysis can be used to differentiate land use & more Existing maps - ordinance survey; historical All have their uses - can be combined with survey data using GIS software (e. g. Arc. GIS) (although corrections may be needed)

Alternative data acquisition Prospection data - spatial sample data