Surfaces Dr Scott Schaefer 1 Types of Surfaces

Surfaces Dr. Scott Schaefer 1

Types of Surfaces Implicit Surfaces n Parametric Surfaces n Deformed Surfaces n 2/59

Implicit Surfaces 3/59

Implicit Surfaces 4/59

Implicit Surfaces n Examples u Spheres u Planes u Cylinders u Cones u Tori 5/59

Intersecting Implicit Surfaces 6/59

Intersecting Implicit Surfaces 7/59

Intersecting Implicit Surfaces n Example u u 8/59

Intersecting Implicit Surfaces n Example u u 9/59

Intersecting Implicit Surfaces n Example u u 10/59

Intersecting Implicit Surfaces n Example u u 11/59

Normals of Implicit Surfaces n Given F(x, y, z)=0, find the normal at a point (x, y, z) 12/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n 13/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n F(x(t), y(t), z(t))=0 n 14/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n F(x(t), y(t), z(t))=0 n 15/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n F(x(t), y(t), z(t))=0 n 16/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n F(x(t), y(t), z(t))=0 n 17/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n F(x(t), y(t), z(t))=0 n Tangent of curve!!! 18/59

Normals of Implicit Surfaces Given F(x, y, z)=0, find the normal at a point (x, y, z) n Assume we have a parametric curve (x(t), y(t), z(t)) on the surface of F(x, y, z) n F(x(t), y(t), z(t))=0 n Normal of surface!!! 19/59

Normals of Implicit Surfaces n Example 20/59

Normals of Implicit Surfaces n Example 21/59

Normals of Implicit Surfaces n Example 22/59

Implicit Surfaces Advantages u Easy to determine inside/outside u Easy to determine if a point is on the surface n Disadvantages u Hard to generate points on the surface n 23/59

Parametric Surfaces Geri’s Game Copyright Pixar 24/59

Parametric Surfaces 25/59

Parametric Surfaces 26/59

Intersecting Parametric Surfaces Solve three equations (one for each of x, y, z) for the parameters t, u, v n Plug parameters back into equation to find actual intersection n 27/59

Intersecting Parametric Surfaces 28/59

Intersecting Parametric Surfaces 29/59

Intersecting Parametric Surfaces 30/59

Intersecting Parametric Surfaces 31/59

Normals of Parametric Surfaces n Assume t is fixed 32/59

Normals of Parametric Surfaces n Assume t is fixed Curve on surface 33/59

Normals of Parametric Surfaces n Assume t is fixed Tangent at s 34/59

Normals of Parametric Surfaces n Assume s is fixed 35/59

Normals of Parametric Surfaces n Assume s is fixed Curve on surface 36/59

Normals of Parametric Surfaces n Assume s is fixed Tangent at t 37/59

Normals of Parametric Surfaces n Normal at s, t is 38/59

Parametric Surfaces Advantages u Easy to generate points on the surface n Disadvantages u Hard to determine inside/outside u Hard to determine if a point is on the surface n 39/59

Deformed Surfaces Assume we have some surface S and a deformation function D(x, y, z) n D(S) is deformed surface n n Useful for creating complicated shapes from simple objects 40/59

Intersecting Deformed Surfaces Assume D(x, y, z) is simple… a matrix n First deform line L(t) by inverse of D n Calculate intersection with undeformed surface S n Transform intersection point and normal by D n 41/59

Intersecting Deformed Surfaces n Example 42/59

Intersecting Deformed Surfaces n Example 43/59

Intersecting Deformed Surfaces n Example 44/59

Intersecting Deformed Surfaces n Example 45/59

Intersecting Deformed Surfaces n Example 46/59

Intersecting Deformed Surfaces n Example 47/59

Normals of Deformed Surfaces Define how tangents transform first n Assume curve C(t) on surface n 48/59

Normals of Deformed Surfaces Define how tangents transform first n Assume curve C(t) on surface n 49/59

Normals of Deformed Surfaces Define how tangents transform first n Assume curve C(t) on surface n Tangents transform by just applying the deformation D!!! 50/59

Normals of Deformed Surfaces n Normals and tangents are orthogonal before and after deformation 51/59

Normals of Deformed Surfaces n Normals and tangents are orthogonal before and after deformation 52/59

Normals of Deformed Surfaces n Normals and tangents are orthogonal before and after deformation 53/59

Normals of Deformed Surfaces n Normals and tangents are orthogonal before and after deformation 54/59

Normals of Deformed Surfaces n Normals and tangents are orthogonal before and after deformation 55/59

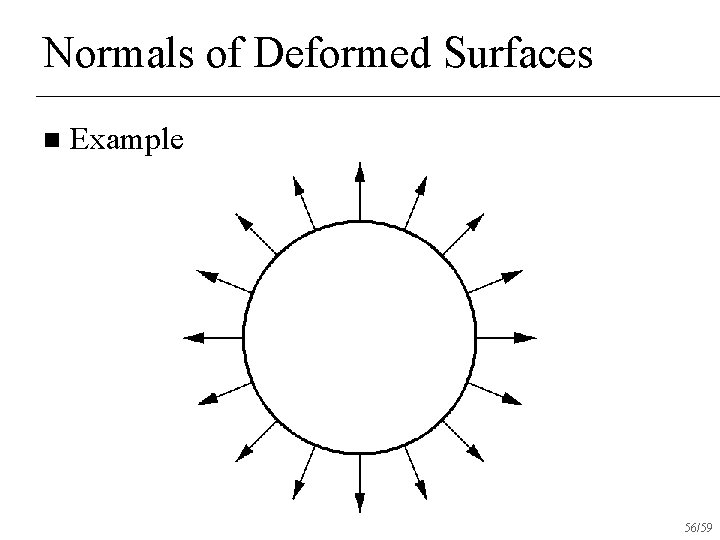
Normals of Deformed Surfaces n Example 56/59

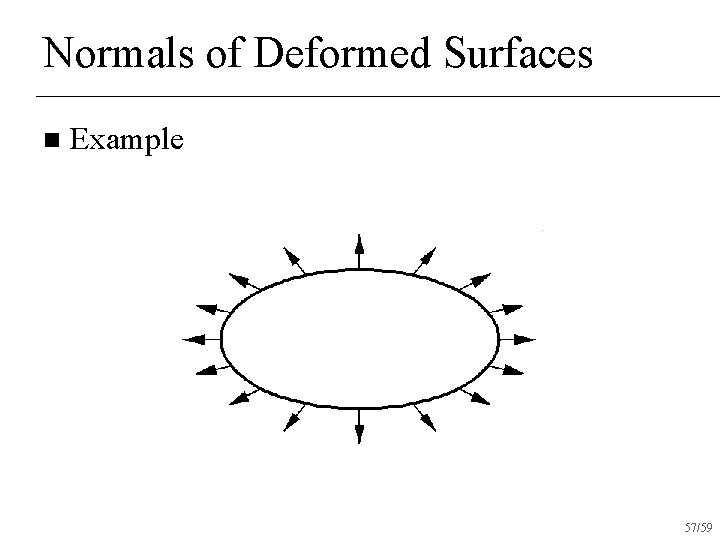
Normals of Deformed Surfaces n Example 57/59

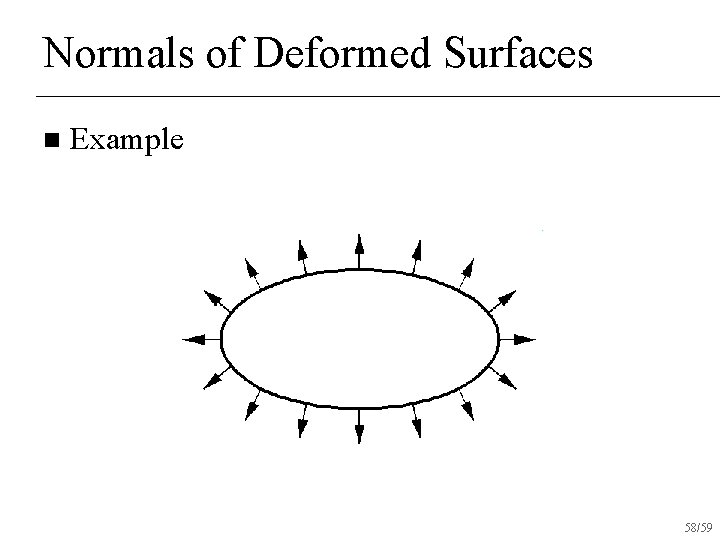
Normals of Deformed Surfaces n Example 58/59

Deformed Surfaces Advantages u Simple surfaces can represent complex shapes u Affine transformations yield simple calculations n Disadvantages u Complicated deformation functions can be difficult to use (inverse may not exist!!!) n 59/59