Surface Integration 1 OUTCOMES By watching this video

Surface Integration 1

OUTCOMES By watching this video student will able to learn how to evaluate surface integration problem. 2

Surface Integration 3

4

If the given surface is not on any plane then outward normal to the surface is “Grad S”. Here there are three examples. All these surfaces are not parallel to any plane. Plane 2 x+3 y+4 z = 12 cylinder sphere In this case unit outward normal to the surface 5

Evaluation of Surface Integral Surface integral is evaluated by reducing it in to double integral over the region R. Where the region R is the orthogonal projection of S on one of the coordinate planes [XY or YZ or ZX planes]. Suppose R be orthogonal projection of S on XY plane then [unit outward normal to S is where are directional cosines of. ] Hence 6

7

Important points If represents velocity of the fluid at any point on a closed surface S, then surface integral represents Flux over S. i. e Volume of the fluid flowing out from S per unit time. If = 0 , then is called Solenoidal vector function. Component form of Surface integral 8

Problem 1: Evaluate where in first octant. and S is part of plane Solution: Given surface S = 2 x + y + 2 z – 6 and Given surface is in first octant. It is not parallel to any plane. Let R be the projection of S on XY plane. 9

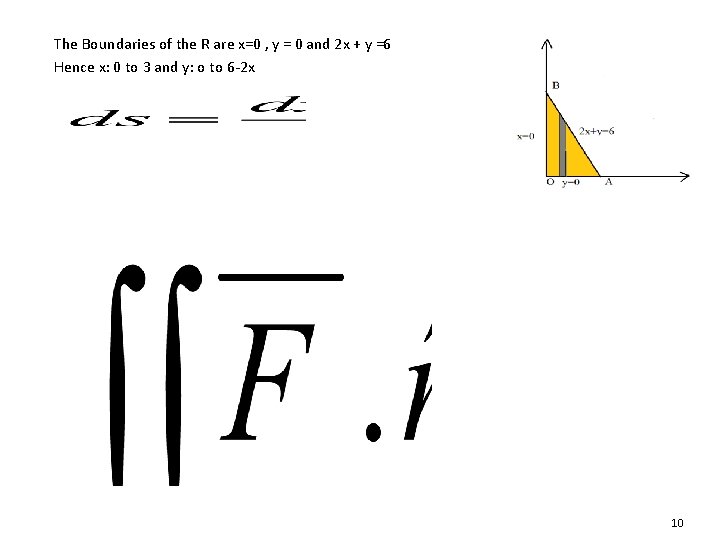
The Boundaries of the R are x=0 , y = 0 and 2 x + y =6 Hence x: 0 to 3 and y: o to 6 -2 x 10

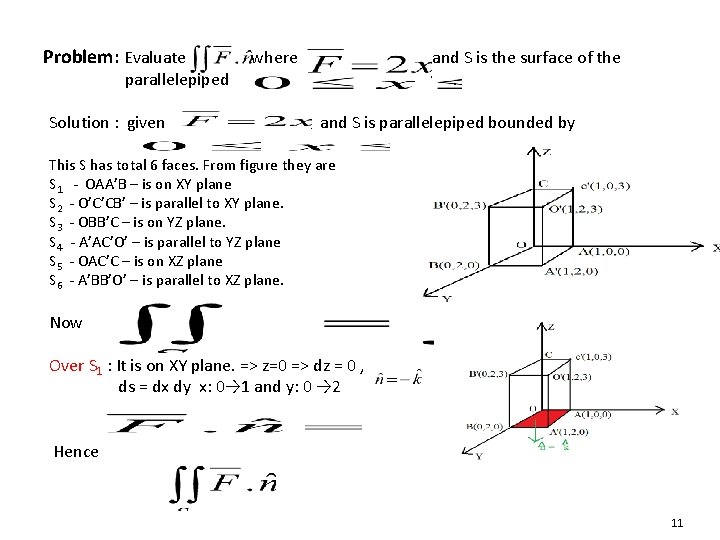
Problem: Evaluate where and S is the surface of the. parallelepiped Solution : given and S is parallelepiped bounded by This S has total 6 faces. From figure they are S 1 - OAA’B – is on XY plane S 2 - O’C’CB’ – is parallel to XY plane. S 3 - OBB’C – is on YZ plane. S 4 - A’AC’O’ – is parallel to YZ plane S 5 - OAC’C – is on XZ plane S 6 - A’BB’O’ – is parallel to XZ plane. Now Over S 1 : It is on XY plane. => z=0 => dz = 0 , ds = dx dy x: 0→ 1 and y: 0 → 2 Hence 11

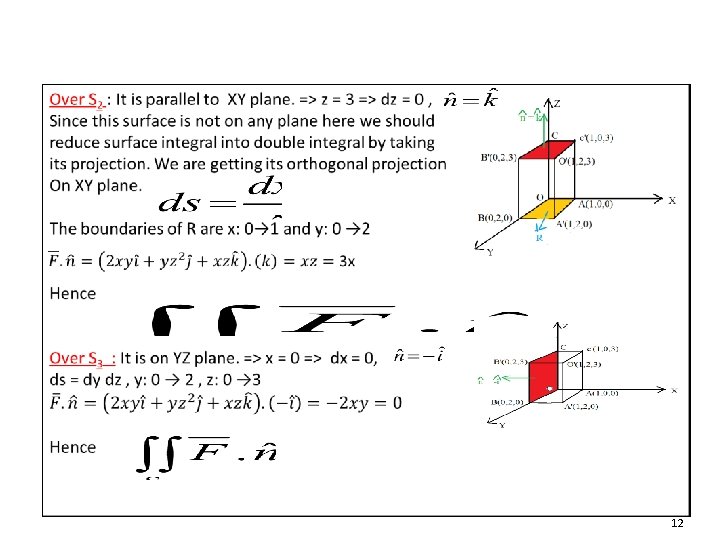
12

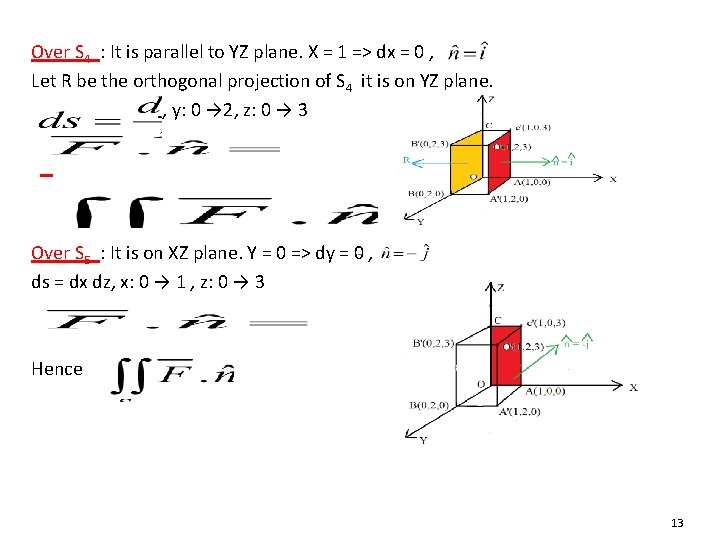
Over S 4 : It is parallel to YZ plane. X = 1 => dx = 0 , Let R be the orthogonal projection of S 4 it is on YZ plane. , y: 0 → 2, z: 0 → 3 Over S 5 : It is on XZ plane. Y = 0 => dy = 0 , ds = dx dz, x: 0 → 1 , z: 0 → 3 Hence 13

Over S 6 : It is parallel to XZ plane. Y = 2 => dy = 0, Let R be the orthogonal projection of S 6 on XZ plane. , x: 0 → 1, z: 0 → 3 Now 14

ASSESMENT 1. If S is a) b) and R is projection of S on XY plane then ds= ______. c) d) 2. If S is surface on YZ plane then ds = ______. a) b) c) d) 3. Unit outward normal to the plane a) b) c) is _____. d) 4. Unit outward normal to the surface of cube which is on XZ plane is _____. a) b) c) d) 5. represents ______. a) Work done by F b) velocity of F c) Flux of F d) acceleration of F 15

Next Lecture Stoke’s theorem Thank you 16