Supporting your child in learning math Marian Small

































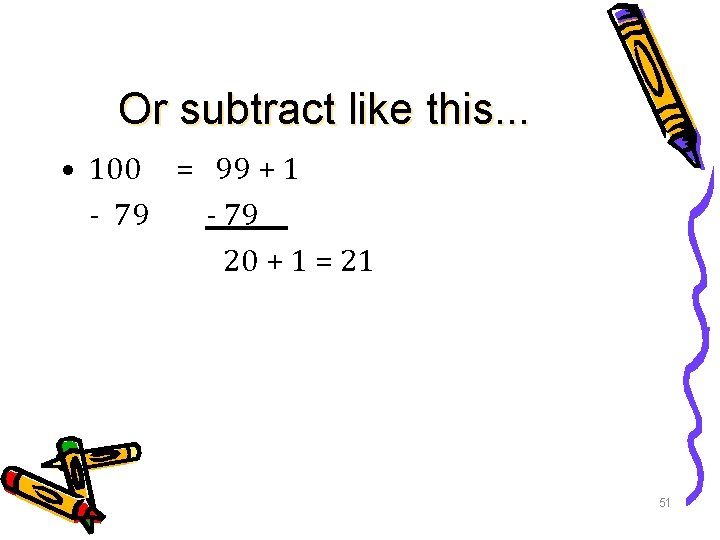

























- Slides: 77

Supporting your child in learning math Marian Small November 2017 1

This morning I will talk about • How the teaching of math has and has not changed • Things you can do to support your child’s math learning 2

What math skills are important in 2017 and beyond? • The world has changed. • In the past, much of early math learning focused on how to efficiently add, subtract, multiply and divide. • But often students did not learn, well enough, when each operation is required. 3

• For example, if the problem were: How many boards that are 4. 2 m long do I need to fill a 17. 59 m space? , a students needs to know whether to add, subtract, multiply or divide. 4

• Although I want students to be able to compute, being quick at it with large numbers matters less when we all have calculators available. • Knowing when to use each needs more of our teaching time. 5

Problem solving • There is also a need, in the society in which we live, to create more students who are good problem solvers- people who can figure things out without being shown first. • Employers regard this as a HUGE need. 6

Historically • Many students, even those who were good at computation, fell down at problem solving. . • So now it gets more emphasis. 7

There are 5 strands in K – 6 math in the Ontario curriculum • • • Number Geometry Measurement Patterns and algebra Data and Probability 8

Most parents • are most concerned about number, so I will start there. 9

Working with numbers • The way we approach the learning of computation has changed in some ways, but not other ways. 10

Little number work • Facts involve computations with small numbers, e. g. 4 + 9 = 13 or 12 – 3 = 9 or 9 x 8 = 72 or 40 ÷ 5 = 8. • Facts remain important because they are fundamental both to estimation and any other calculations. 11

We used to believe… • The best way to learn facts is to sit down and memorize them by saying them over and over. • And that being super fast with them is really important. 12

Now we realize… • that a child is better off if he or she has tools to recall something he or she may have memorized but may forget. • We call these strategies. 13

For example… • Whenever you add something to 9, we focus on the notion that you could, instead, add the number that is 1 less to 10. • e. g. 9 + 8 = 10 + 7 • Later 299 + 215 = 300 + 214. 14

There is now research that shows… • That even though some kids memorize well. . • for kids who are anxious about math or get nervous having to be quick, old strategies doom them to failure. 15

There is now research that shows… • Brain research shows that when a student is anxious, it is very hard for him or her to recall facts, even if they know them(Sian Bellock) • We now approach fact learning in different ways for different kids. 16

So we teach principles and strategies • For example, we spend time with kids helping them know (just like you and I did) that 14 = 10 + 4, that 18 = 10 + 8, etc. • There is no work to adding 10 + 4; it’s just what 14 is. 17

Then • We spend LOTS of time getting kids good at adding numbers that add to 10 and then use those to figure out other questions. • For example 8 + 5 is 8 + 2 and then another 3, but 10 + 3 is 13. 18

So we teach principles and strategies • For some reason, people learn doubles quickly, so to figure out 7 + 8, we help kids think: 7 + 7 and then 1 more. 19

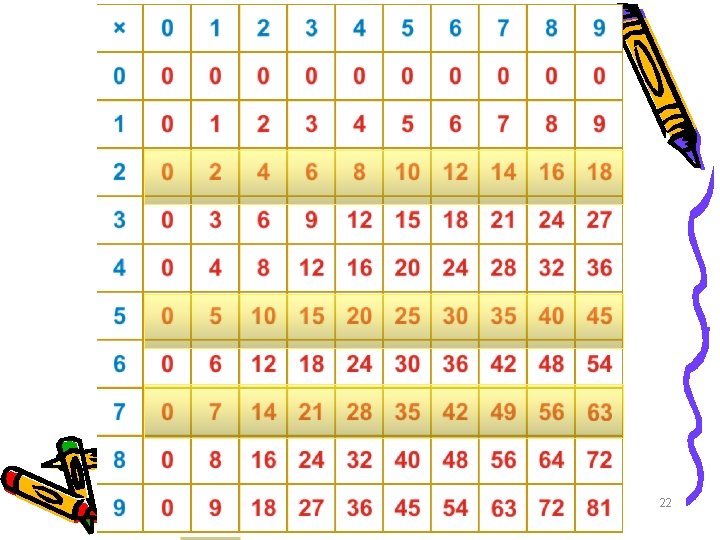
For multiplication • We help kids see that to figure out 4 x 7, you could really think 4 x 5 + 4 x 2. o o o o o x x x x 20

Many of these principles can be. . • Seen on addition and multiplication tables • visualized using diagrams or objects 21

22

We use new tools • We now use many visual/concrete materials so students can “see” the math ideas. • A long body of research has shown their value in making math make sense to kids and in improving performance. 23

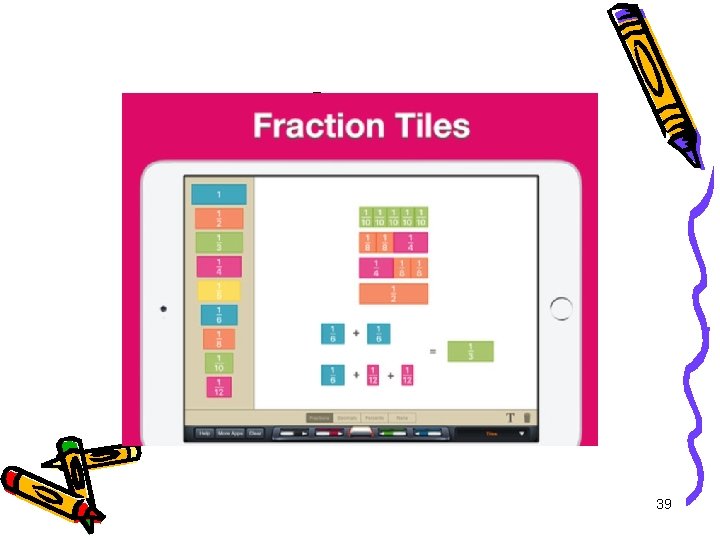
Accessing virtual manipulatives • There are tools for materials your children use in class freely available on line. • Many are also available as apps. 24

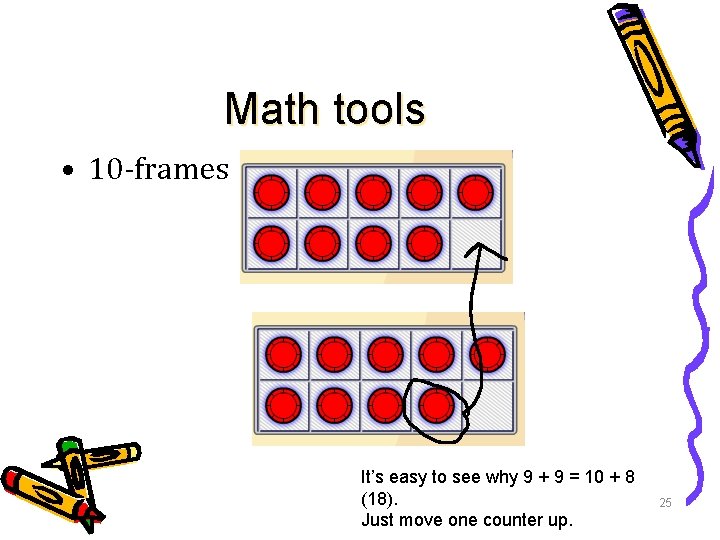
Math tools • 10 -frames It’s easy to see why 9 + 9 = 10 + 8 (18). Just move one counter up. 25

Pattern Blocks • http: //oame. on. ca/CLIPS/swf. Player. htm l? swf. URL=tools/ub. Pattern. Blocks. Tool. Cr eator. swf 26

Pattern Blocks • http: //oame. on. ca/CLIPS/swf. Player. htm l? swf. URL=tools/ub. Pattern. Blocks. Tool. Cr eator. swf 27

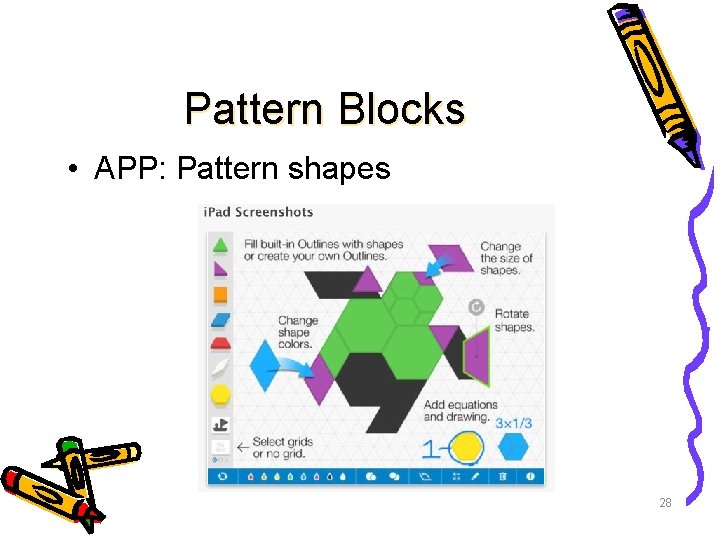
Pattern Blocks • APP: Pattern shapes 28

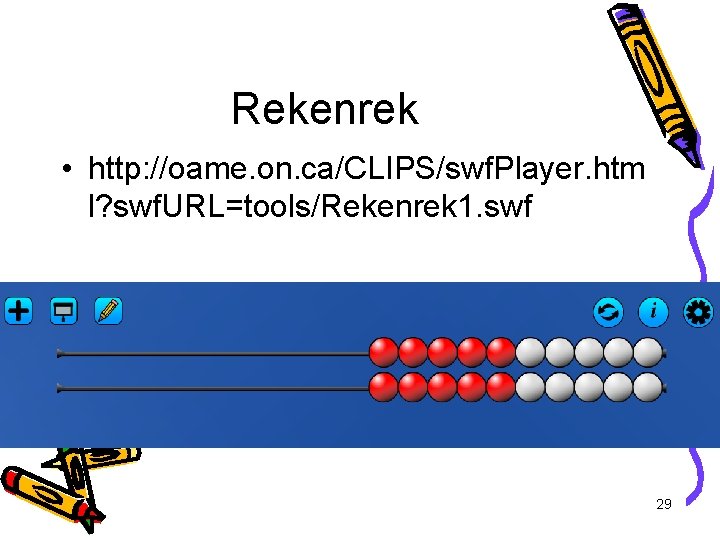
Rekenrek • http: //oame. on. ca/CLIPS/swf. Player. htm l? swf. URL=tools/Rekenrek 1. swf 29

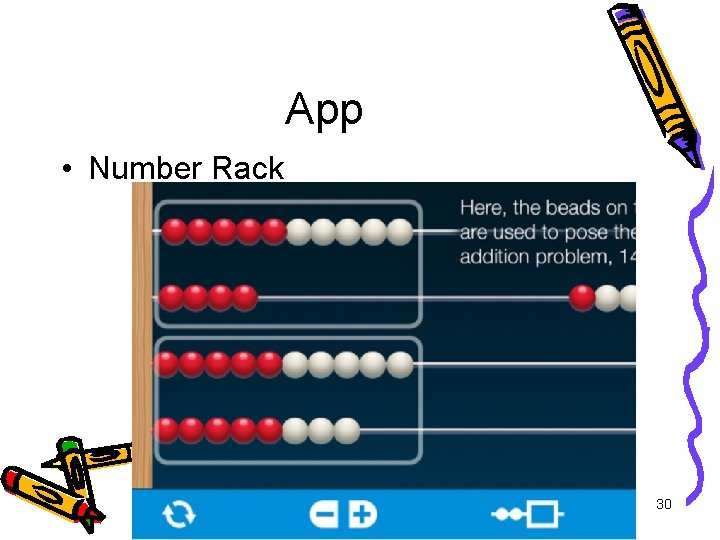
App • Number Rack 30

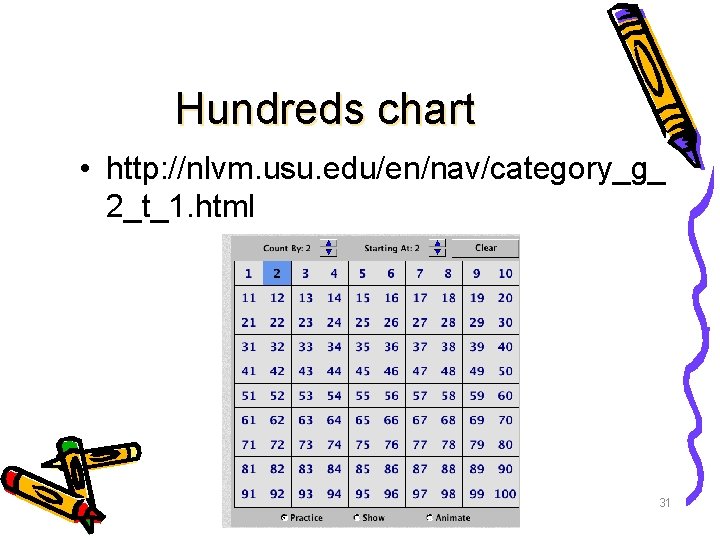
Hundreds chart • http: //nlvm. usu. edu/en/nav/category_g_ 2_t_1. html 31

App • Interactive Hundred chart 32

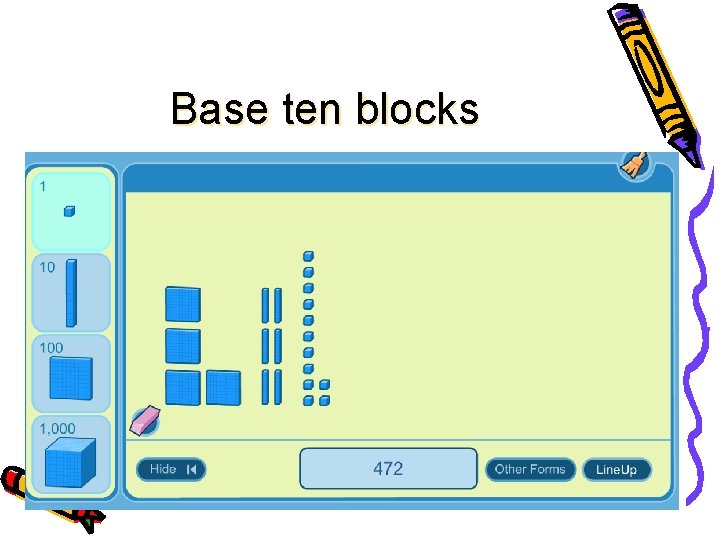
Base ten blocks • https: //wwwk 6. thinkcentral. com/content/hsp/math/h spmath/na/gr 35/itools_intermediate_9780547274058_ /basetenblocks. html 33

Base ten blocks 34

App • Base ten blocks math 35

Relational rods • http: //oame. on. ca/CLIPS/swf. Player. htm l? swf. URL=tools/ub. Relational. Rods. Creat or. swf 36

App • Number rods 37

Fraction bars • http: //oame. on. ca/CLIPS/swf. Player. htm l? swf. URL=tools/Fraction. Strips 1. swf&titl e=Fraction%20 Strips 38

Or 39

Geometric shapes • http: //illuminations. nctm. org/Activity. asp x? id=3521 40

Attention to estimation • There is increasingly more focus on estimation and mental strategies, when appropriate, when dealing with larger numbers (e. g. 3 - digit, 4 –digit) and decimals. 41

Estimation • I need kids who quickly see that 35 x 49 must be around 1500, not just kids who get the answer; often an estimate is all this is needed to see if your calculator answer makes sense. 42

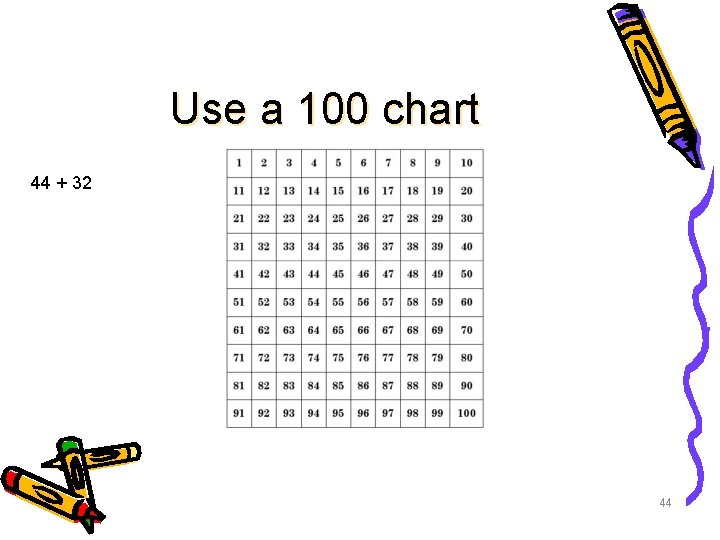
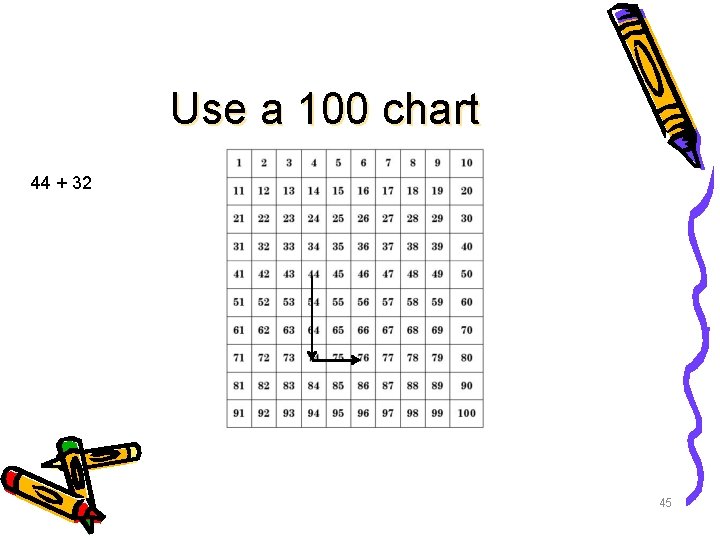
For mental strategies • Here is an interesting mental strategy we often teach younger kids for adding and subtracting. 43

Use a 100 chart 44 + 32 44

Use a 100 chart 44 + 32 45

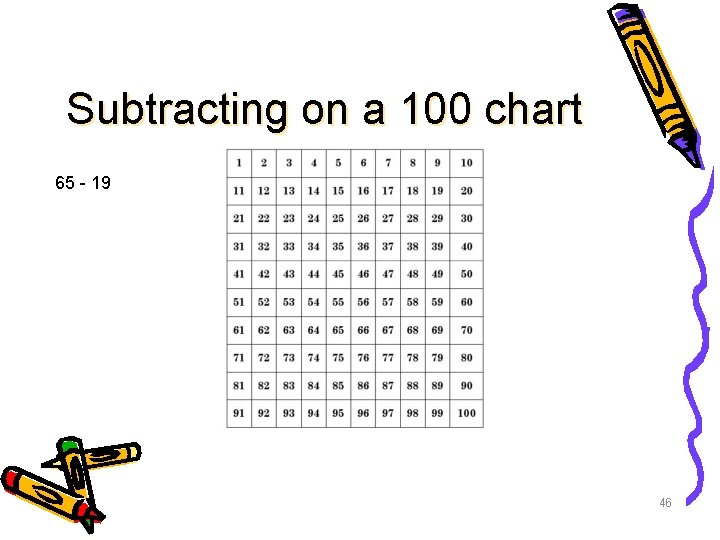
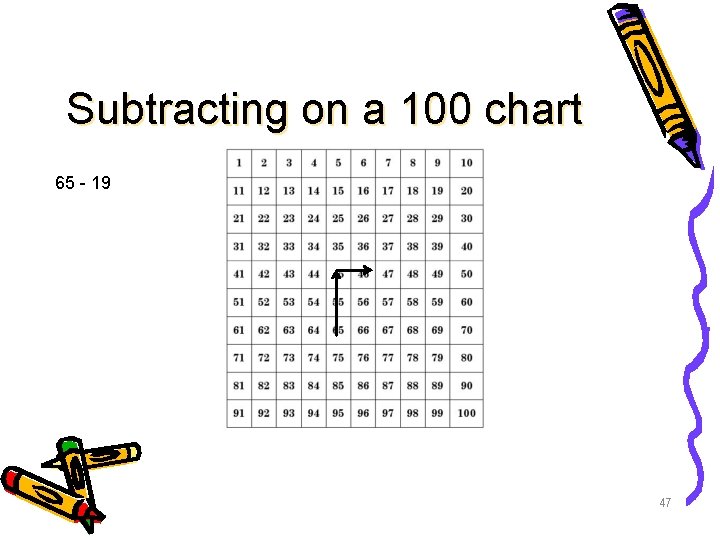
Subtracting on a 100 chart 65 - 19 46

Subtracting on a 100 chart 65 - 19 47

Alternative strategies that might seem new • How would you calculate 342 – 121? • Would you do 200 – 2 the same way? • Children are learning different strategies since different ones are more efficient or more meaningful in different situations AND • Different ones make more sense to different kids. 48

For example • It is reasonable and correct to add like this: 38 + 47 70 + 15 85 49

For example • It is reasonable and correct to add like this: 38 + 47: Think 38 + 50 = 88 and then subtract 3 to get 85. 50
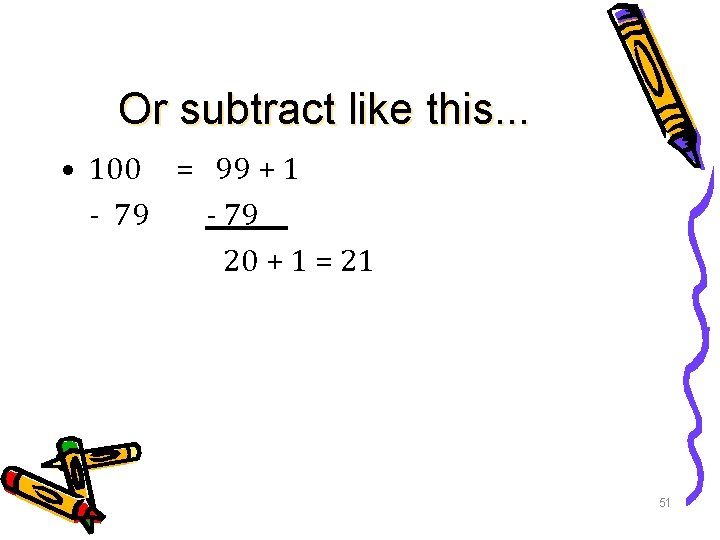
Or subtract like this. . . • 100 = 99 + 1 - 79 20 + 1 = 21 51

Teaching through problem solving • We show kids we have faith that they can figure things out. • What happens is that as they solve a problem, they clarify a lot of ideas. 52

I might ask… • • I bought 5 items and spent $315. Two were the same price. One cost a lot more than the others. What could each have cost? 53

I might ask • The volume of a box is 100 cm 3. • What could the length, width, and height be? 54

Collaboration • Kids will be working together more to learn since most of us learn better in talking with others. 55

Do they all have to do exactly the same thing? • We might offer two or more tasks for students to choose from. • The tasks will be similar in nature, although one might be slightly less complicated than the other. • This serves different needs better than we used to in the past. 56

What can you do? • Our big question as parents is what we can do to help our child. 57

Number Play Lots of children respond well to “magic”. For example: 58

Number Play Choose a number. Add it to itself. Add 5 Add 6. Subtract 1 Divide by 2 Tell me your answer and I will tell your number. 59
How many…. ? • • • Spoons in the drawer? Steps to get downstairs? Trees on the street? Sections in an orange? Windows in the house? 60

Interesting Questions • How long is long hair? • How long would it take to count to 100? • How far could you go in 100 steps? 61

Support involves… • Not showing, but probing. • Asking why this or why that… • Building connections 62

You might • Encourage kids to “teach you” what they learned or explain their thinking to you. 63

Games • You could play games where you make up the rules or use existing games to practise skills. 64

Games to Play • 2 players • Each rolls two dice. The score is the sum. • The first player to get to 100 wins. 65

Games to Play • 2 players • Each rolls two dice. The score is 2 x one value + the other. • The first player to get to 100 wins. 66

Board games 67

Box cars and one eyed jacks • http: //www. boxcarsandoneeyedjacks. co m/ 68

You could solve interesting problems 69

How much is your name worth? A B C D E F G H I 1 2 3 4 5 6 7 8 9 J K L M N O P Q R 10 11 12 13 14 15 16 17 18 S T U V W X Y Z 19 20 21 22 23 25 26 24 70

What words are worth 40 – 50? A B C D E F G H I 1 2 3 4 5 6 7 8 9 J K L M N O P Q R 10 11 12 13 14 15 16 17 18 S T U V W X Y Z 19 20 21 22 23 25 26 24 71

Figure this • http: //www. figurethis. org 72

Figure this 73

Useful web sites • http: //www. dreambox. com/parent-resources • http: //www. cbc. ca/news/health/back-to-school-2015 parents-math-anxiety-can-pass-to-kids-psychologists-say 1. 3207956 74

Useful web sites • https: //www. edu. gov. on. ca/eng/literacynume racy/parent. Guide. Num. En. pdf • http: //www. ocdsb. ca/med/pub/OCDSB_Publi cations/Numeracy%20 Parent%20 Guide. pdf 75

What is success? • Not just a mark • Enjoying the math • Seeing math around them 76

You need to… • Show that you enjoy math too. • Show confidence- believe that they can if you give them the time. • Emphasize good thinking, not speed. • Emphasize good thinking, not mistakes. 77