Support Vector Machines part 2 Face Recognition Biometric

Support Vector Machines (part 2) Face Recognition & Biometric Systems

Plan of the lecture SVM – main issues repeated Soft margin Multi-class problems Applications to face recognition Training set optimization Face Recognition & Biometric Systems

SVM – main issues Aim: data classification Two stages: n n learning (training) classification Face Recognition & Biometric Systems

SVM – main issues Solves linearly separable problems Input data are transformed n mapping into higher dimensions Training: find optimal hyperplane n margin maximisation Face Recognition & Biometric Systems

SVM – main issues A function: Data mapping: x (x) Dot product used in all calculations Dot product -> kernel of convolution No need to know the function Face Recognition & Biometric Systems

Convolution kernels Linear Polynomial RBF (radial basis functions) Face Recognition & Biometric Systems

SVM – main issues Optimal hyperplane: n w 0 • x + b 0 = 0 for 2 D data it is a line Optimal margin width: Face Recognition & Biometric Systems

SVM – main issues Optimal hyperplane: n n yi – class label i – Lagrange multipliers (obtained during optimisation) Face Recognition & Biometric Systems

SVM – main issues Lagrange coefficients ( ): n n n calculated for every vector from the training set non-zero for support vectors equal zero for the majority of vectors Training set after the optimisation: n n n support vectors coefficients for every vector number of vectors reduced Face Recognition & Biometric Systems

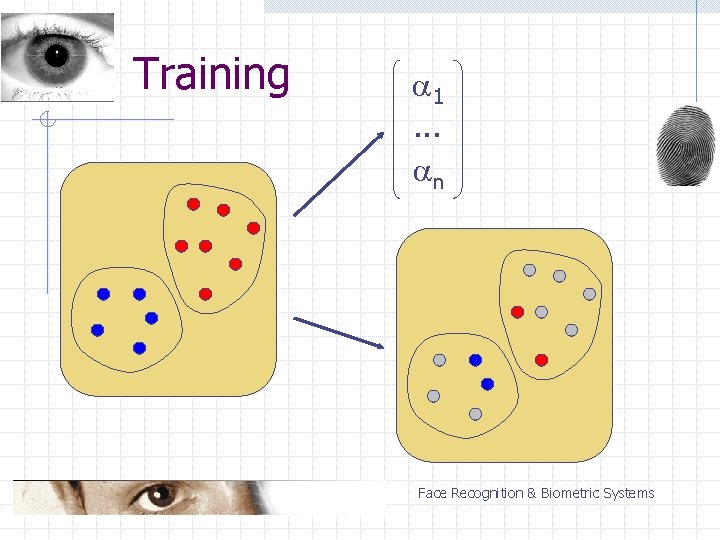
Training 1. . . n Face Recognition & Biometric Systems

SVM – main issues Classification of a vector: xr, xs – support vectors from opposite classes Face Recognition & Biometric Systems

Soft margin Error allowed during the training: Number of errors minimised Optimised function must be modified Face Recognition & Biometric Systems

Soft margin Margin maximisation Minimisation of functional (F – monotonic, convex function): C – penalty parameter n presentation Constraints: Face Recognition & Biometric Systems

Soft margin Optimisation without the soft margin: Face Recognition & Biometric Systems

Soft margin Optimisation with the soft margin (for F(u) = u 2): Face Recognition & Biometric Systems

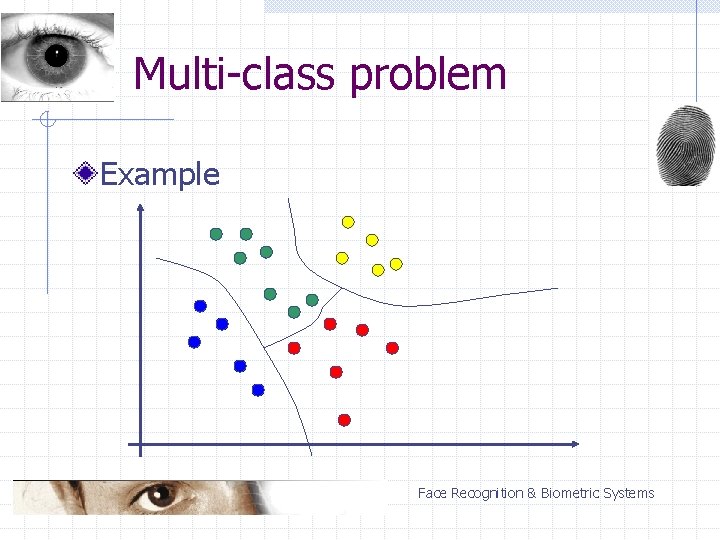
Multi-class problem Example Face Recognition & Biometric Systems

Multi-class problem Based on two-class problem n solved by the SVM N classes in the training set Possible solutions: n n n base-class approach 1 – N comparisons 1 – 1 comparisons Face Recognition & Biometric Systems

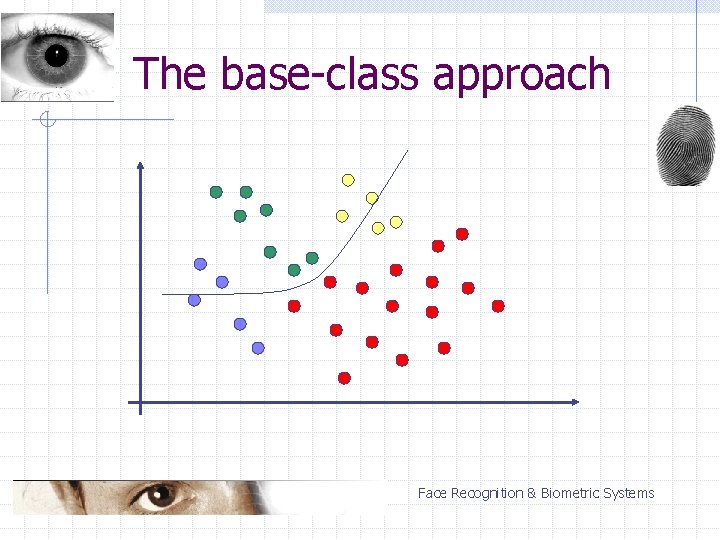
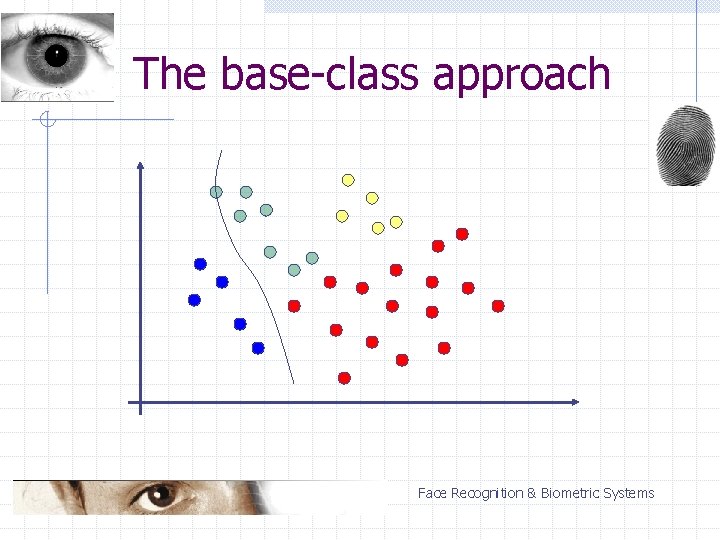
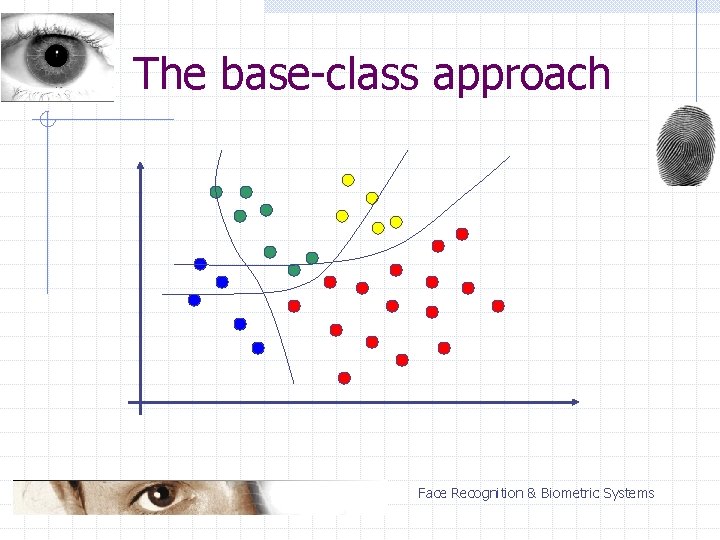
The base-class approach n n n one class selected as a base class each class compared with the base class the strongest response decides Classification of a single vector: n (N – 1) two-classifications Face Recognition & Biometric Systems

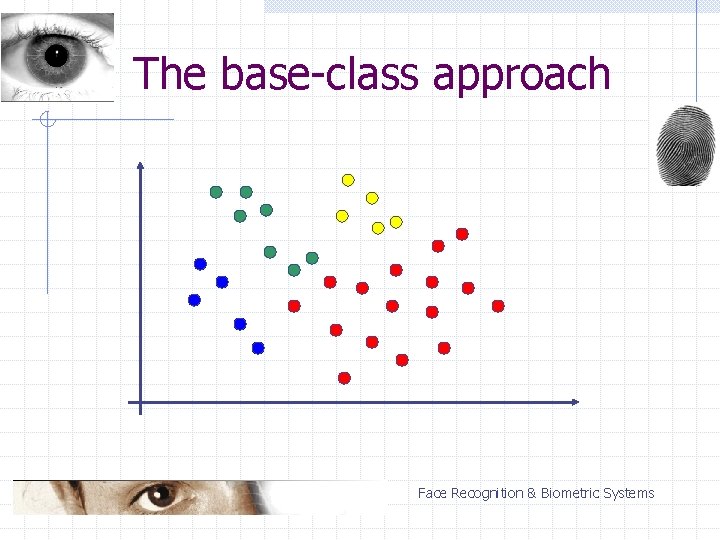
The base-class approach Face Recognition & Biometric Systems

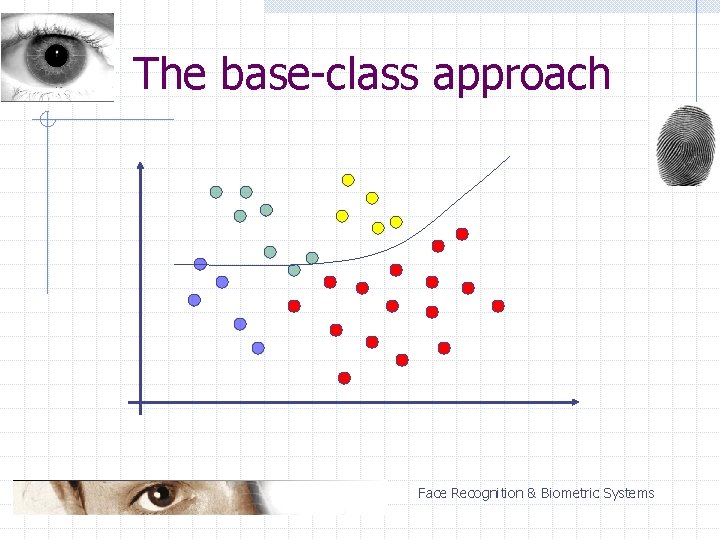
The base-class approach Advantages: n n high speed effective when non-base classes are easily separable Disadvantages: n problems with separating non-base classes Face Recognition & Biometric Systems

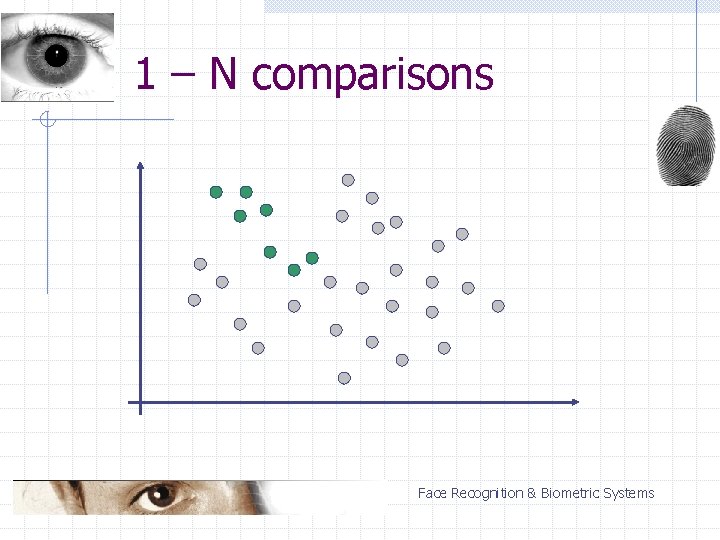
1 – N comparisons Each class compared with the rest The strongest response decides Classification of a single vector: n N two-classifications Compared to the base-class approach: n n more universal (symmetry) comparable speed Face Recognition & Biometric Systems

1 – N comparisons Face Recognition & Biometric Systems

1 – 1 comparisons Each class compared with each other The highest precision Classification of a single vector: n N(N – 1)/2 two-classifications Very slow method Face Recognition & Biometric Systems

SVM for face recognition Detection and verification Feature vectors comparison Multi-method fusion Other applications Face Recognition & Biometric Systems

Face detection Ellipse detection n n Generalised Hough Transform a set of face candidates Normalisation of the candidates Verification n n image (as a vector) classified by the SVM multi-class approach Face Recognition & Biometric Systems

Feature vectors comparison Aim: measure similarity between feature vectors Distance-based similarity: n n Euclidean distance Mahalanobis distance Similarity measured by the SVM: n n two vectors subtracted from each other create a difference vector classified K 11 K 21 K 12 K 22 . . . K 1 n K 2 n Face Recognition & Biometric Systems

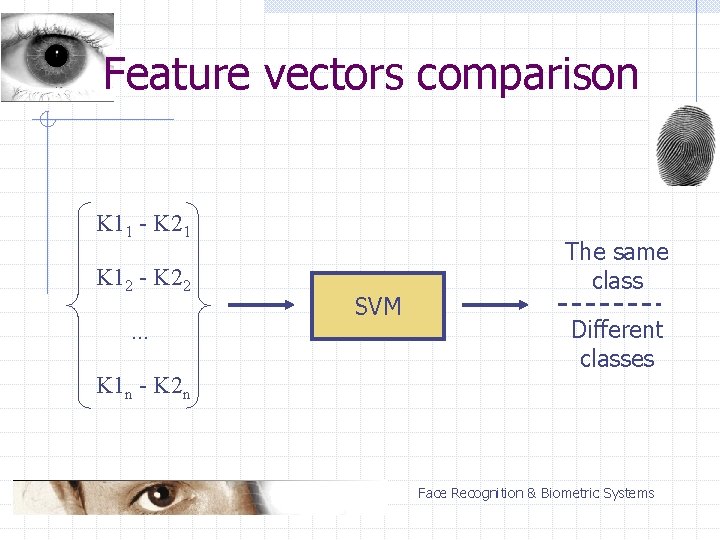
Feature vectors comparison K 11 - K 21 K 12 - K 22. . . K 1 n - K 2 n SVM The same class Different classes Face Recognition & Biometric Systems

Feature vectors comparison Good improvement for EBGM Eigenfaces not improved n similar results to other metrics Face Recognition & Biometric Systems

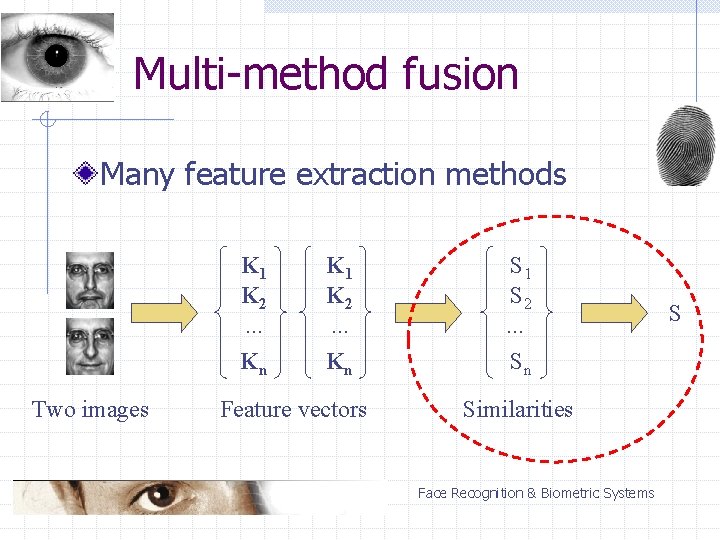
Multi-method fusion Many feature extraction methods K 1 K 2. . . Kn Two images K 1 K 2. . . Kn Feature vectors S 1 S 2. . . Sn Similarities Face Recognition & Biometric Systems S

Multi-method fusion Vector of similarities classified n n n linear kernel polynomial kernel time-consuming classification SVM applied only for the training n n linear kernel – weights for the methods (dimensions stand for methods) average mean based on the weights Face Recognition & Biometric Systems

Other applications Assessment of recognition accuracy n n vector of sorted similarities to the elements in the gallery can be used for many images of the same person Image quality estimation n e. g. elimination of blurred images Face Recognition & Biometric Systems

SVM – limitations Constant and small number of classes n too much time-consuming for many classes Training set: n n must be representative optimal number of elements The parameters must be tuned n Relevance Vector Machines Face Recognition & Biometric Systems

Training set optimization Representative training set: n n n similarity to the classified data universal classification rules difficult to acquire Real training sets: n n n data acquired automatically low quality, faulty data large number of data Face Recognition & Biometric Systems

Training set optimization Selection of available data n n subset drawn randomly genetic algorithms Genetic algorithms n n n heuristic optimization technique evolutional strategy population of individuals fitness genetic operators: w selection w mutation w crossover Face Recognition & Biometric Systems

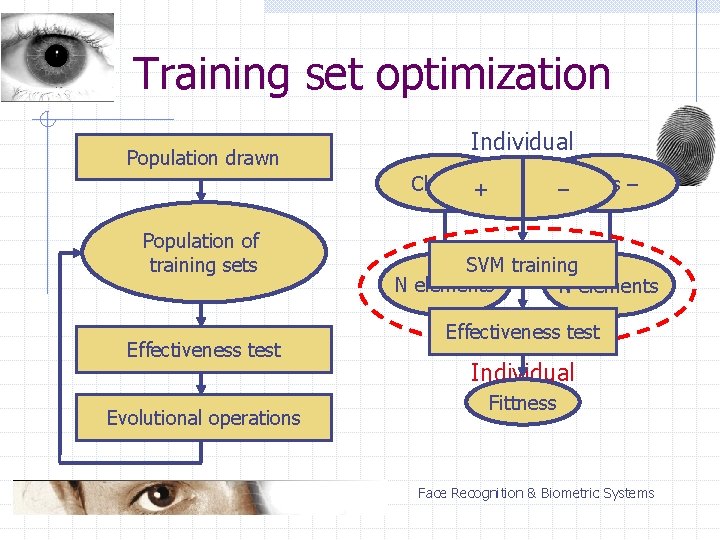
Training set optimization Population drawn Individual Class ++ Population of training sets Effectiveness test Evolutional operations – Class – SVM training N elements Effectiveness test Individual Fittness Face Recognition & Biometric Systems

SVM compared to ANN Support Vector Machines: n n more transparent calculations more controllable than neural networks implements various types of ANN useful for image processing Artificial Neural Networks: n n more applications (e. g. compression) dedicated hardware solutions Face Recognition & Biometric Systems

Summary Soft margin – automatic selection Multi-class problems: n n can be solved basing on two-class problems various approaches Many possible applications in the area of face recognition Training set optimization Face Recognition & Biometric Systems

Thank you for your attention! Next time: Elastic Bunch Graph Matching Face Recognition & Biometric Systems