Support Vector Machines Graphic generated with Lucent Technologies

Support Vector Machines Graphic generated with Lucent Technologies Demonstration 2 -D Pattern Recognition Applet at http: //svm. research. bell-labs. com/SVT/SVMsvt. html

Separating Line (or hyperplane) Class -1 n Class 1 Goal: Find the best line (or hyperplane) to separate the training data. How to formalize? – In two dimensions, equation of the line is given by: – Better notation for n dimensions: David R. Musicant 2

Simple Classifier n The Simple Classifier: – Points that fall on the right are classified as “ 1” – Points that fall on the left are classified as “-1” n Therefore: using the training set, find a hyperplane (line) so that n This is a perceptron! How can we improve on the perceptron? n Class -1 David R. Musicant Class 1 3

Finding the Best Plane n Not all planes are equal. Which of the two following planes shown is better? Class -1 n n n Class 1 Both planes accurately classify the training set. The green plane is the better choice, since it is more likely to do well on future test data. The green plane is further away from the data. David R. Musicant 4

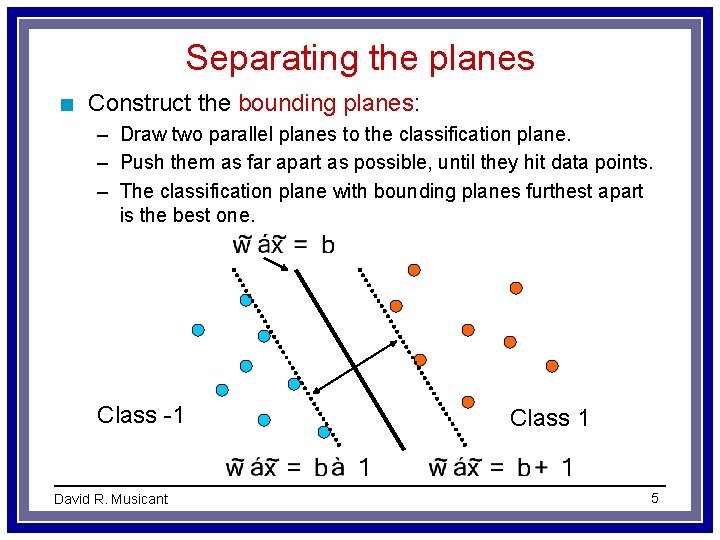
Separating the planes n Construct the bounding planes: – Draw two parallel planes to the classification plane. – Push them as far apart as possible, until they hit data points. – The classification plane with bounding planes furthest apart is the best one. Class -1 David R. Musicant Class 1 5

Recap: Finding the Best Plane n Details – All points in class 1 should be to the right of bounding plane 1. – All points in class -1 should be to the left of bounding plane -1. – Pick yi to be +1 or -1 depending on the classification. Then the above two inequalities can be written as one: – The distance between bounding planes should be maximized. – The distance between bounding planes is given by: Class -1 David R. Musicant Class 1 6

The Optimization Problem n The previous slide can be rewritten as: such that n This is a mathematical program. – Optimization problem subject to constraints – More specifically, this is a quadratic program – There are high powered software tools for solving this kind of problem (both commercial and academic) n No special algorithms are necessary (in theory. . . ) – Just enter this problem and the associated data into a quadratic programming solver (like CPLEX), and let it find an answer. David R. Musicant 7

Data Which is Not Linearly Separable n What if a separating plane does not exist? error Class -1 n n Class 1 Find the plane that maximizes the margin and minimizes the errors on the training points. Take original inequality and add a slack variable to measure error: David R. Musicant 8

The Support Vector Machine n Push the planes apart and minimize the error at the same time: such that n n n C is a positive number that is chosen to balance these two goals. This problem is called a Support Vector Machine, or SVM. The SVM is one of many techniques for doing supervised machine learning – Others: Neural networks, decision trees, k-nearest neighbor David R. Musicant 9

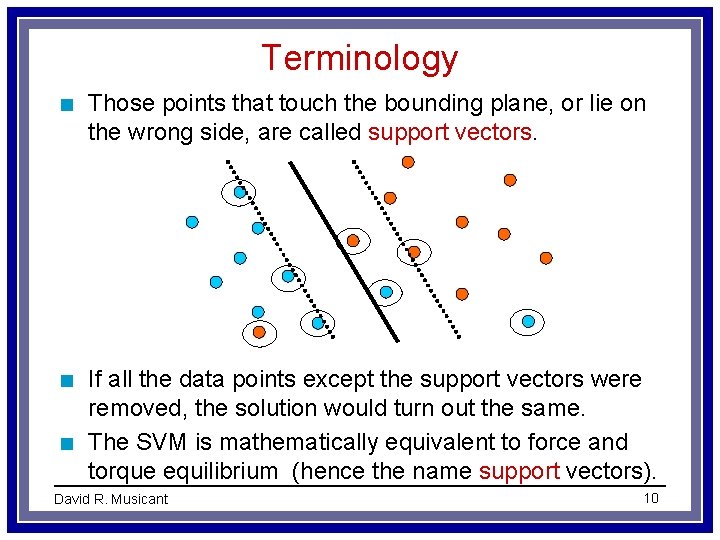
Terminology n Those points that touch the bounding plane, or lie on the wrong side, are called support vectors. n If all the data points except the support vectors were removed, the solution would turn out the same. The SVM is mathematically equivalent to force and torque equilibrium (hence the name support vectors). n David R. Musicant 10

Research: Solving Massive SVMs n The standard SVM is solved using a canned quadratic programming (QP) solver. Problem: – Standard tools bring all the data into memory. If dataset is bigger than memory, out of luck. n n How do other supervised learning techniques handle data that does not fit in memory? Why not use virtual memory? Let the operating system manage which data the QP solver is using. – Answer: The QP solver accesses data in a random, not a continuous fashion. The cost to page data in and out of memory is enormous. David R. Musicant 11

What about nonlinear surfaces? n n n Some datasets may not be best separated by a plane. How can we do nonlinear separating surfaces? Simple method: Map into a higher dimensional space, and do the same thing we have already done. Generated with Lucent Technologies Demonstration 2 -D Pattern Recognition Applet at http: //svm. research. bell-labs. com/SVT/SVMsvt. html David R. Musicant 12

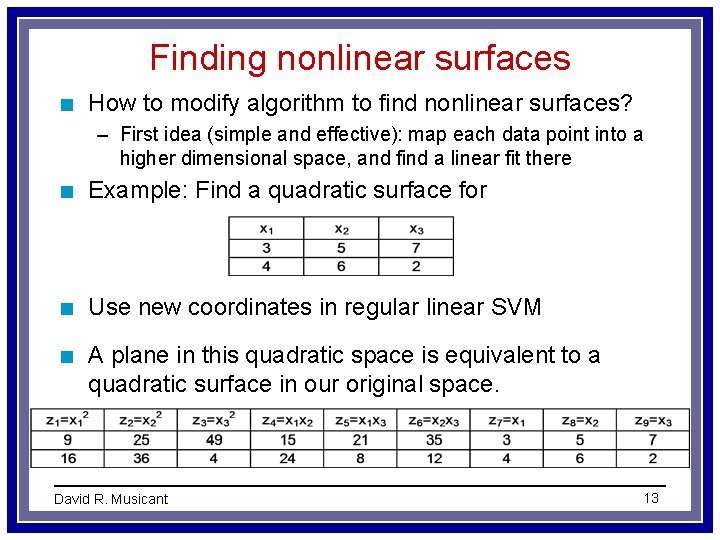
Finding nonlinear surfaces n How to modify algorithm to find nonlinear surfaces? – First idea (simple and effective): map each data point into a higher dimensional space, and find a linear fit there n Example: Find a quadratic surface for n Use new coordinates in regular linear SVM n A plane in this quadratic space is equivalent to a quadratic surface in our original space. David R. Musicant 13

Problem & Solution n If dimensionality of space is high, lots of calculations – For a high polynomial space, combinations of coordinates explodes – Need to do all these calculations for all training points, and for each testing point – Infinite dimensional spaces impossible n Nonlinear surfaces can be used without these problems through the use of a kernel function. – Demonstration: http: //svm. cs. rhul. ac. uk/pagesnew/GPat. shtml David R. Musicant 14

Example: Checkerboard David R. Musicant 15

5 -Nearest Neighbor David R. Musicant 16

Sixth degree polynomial kernel David R. Musicant 17