Support Vector Machines CSE 6363 Machine Learning Vassilis






















































































- Slides: 137

Support Vector Machines CSE 6363 – Machine Learning Vassilis Athitsos Computer Science and Engineering Department University of Texas at Arlington 1

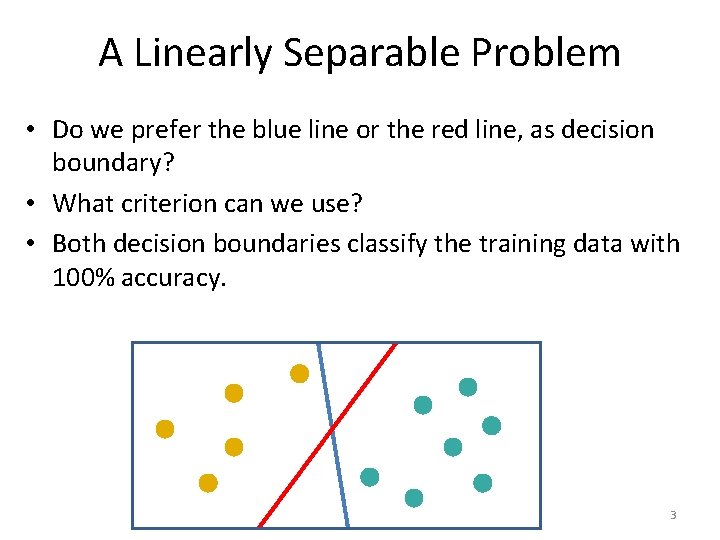
A Linearly Separable Problem • Consider the binary classification problem on the figure. – The blue points belong to one class, with label +1. – The orange points belong to the other class, with label -1. • These two classes are linearly separable. – Infinitely many lines separate them. – Are any of those infinitely many lines preferable? 2

A Linearly Separable Problem • Do we prefer the blue line or the red line, as decision boundary? • What criterion can we use? • Both decision boundaries classify the training data with 100% accuracy. 3

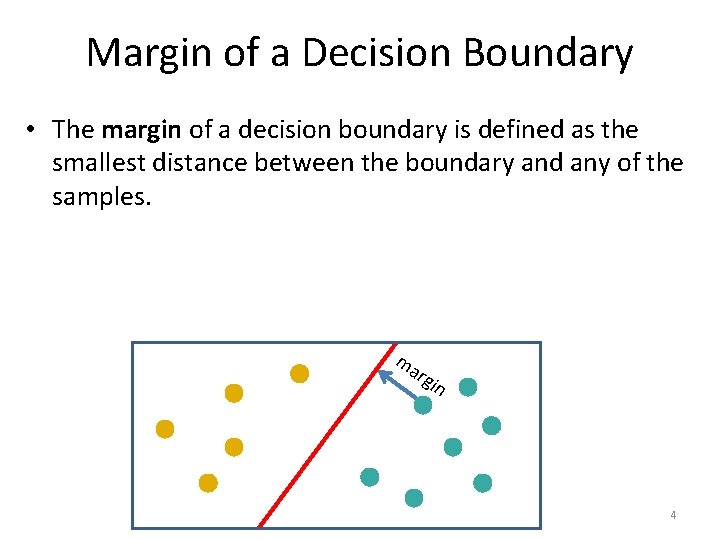
Margin of a Decision Boundary • The margin of a decision boundary is defined as the smallest distance between the boundary and any of the samples. ma rgi n 4

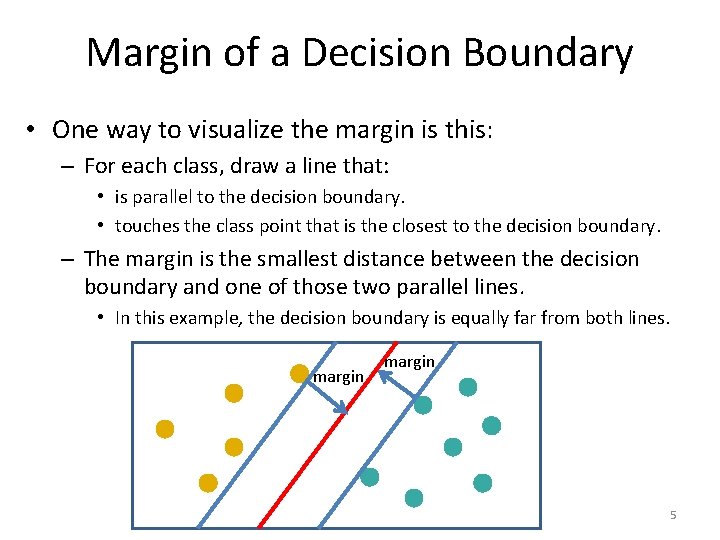
Margin of a Decision Boundary • One way to visualize the margin is this: – For each class, draw a line that: • is parallel to the decision boundary. • touches the class point that is the closest to the decision boundary. – The margin is the smallest distance between the decision boundary and one of those two parallel lines. • In this example, the decision boundary is equally far from both lines. margin 5

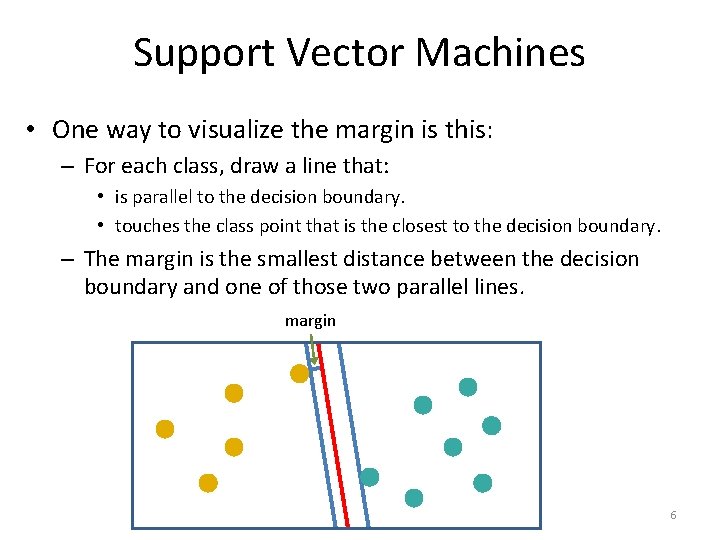
Support Vector Machines • One way to visualize the margin is this: – For each class, draw a line that: • is parallel to the decision boundary. • touches the class point that is the closest to the decision boundary. – The margin is the smallest distance between the decision boundary and one of those two parallel lines. margin 6

Support Vector Machines • Support Vector Machines (SVMs) are a classification method, whose goal is to find the decision boundary with the maximum margin. – The idea is that, even if multiple decision boundaries give 100% accuracy on the training data, larger margins lead to less overfitting. – Larger margins can tolerate more perturbations of the data. margin 7

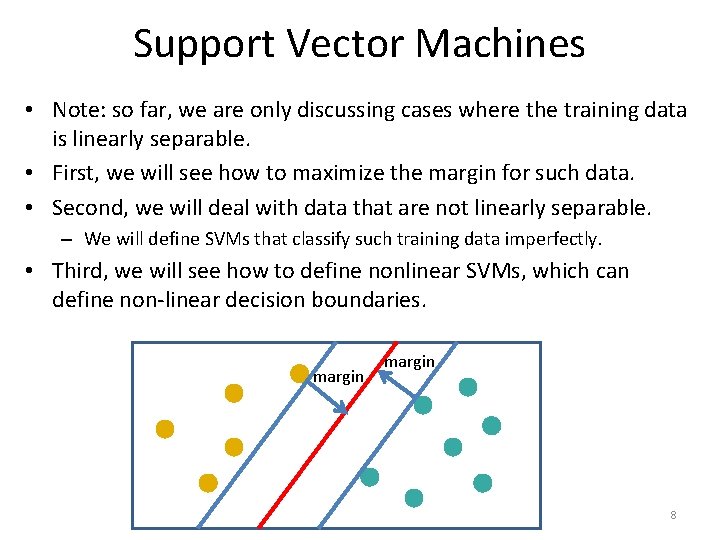
Support Vector Machines • Note: so far, we are only discussing cases where the training data is linearly separable. • First, we will see how to maximize the margin for such data. • Second, we will deal with data that are not linearly separable. – We will define SVMs that classify such training data imperfectly. • Third, we will see how to define nonlinear SVMs, which can define non-linear decision boundaries. margin 8

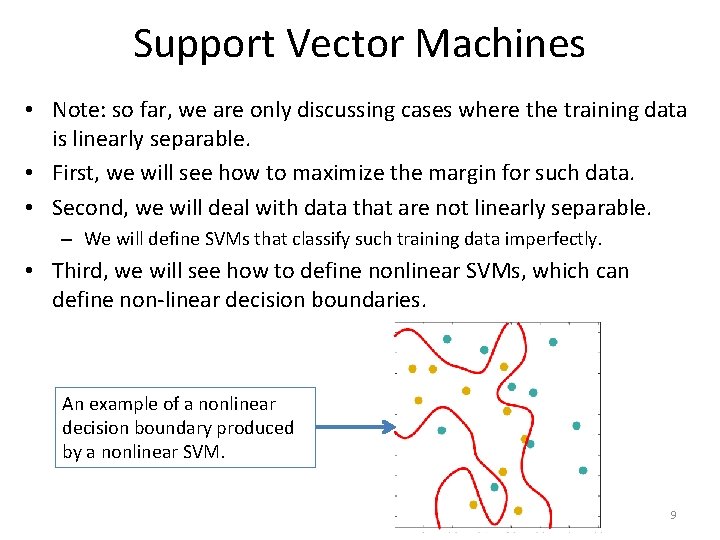
Support Vector Machines • Note: so far, we are only discussing cases where the training data is linearly separable. • First, we will see how to maximize the margin for such data. • Second, we will deal with data that are not linearly separable. – We will define SVMs that classify such training data imperfectly. • Third, we will see how to define nonlinear SVMs, which can define non-linear decision boundaries. An example of a nonlinear decision boundary produced by a nonlinear SVM. 9

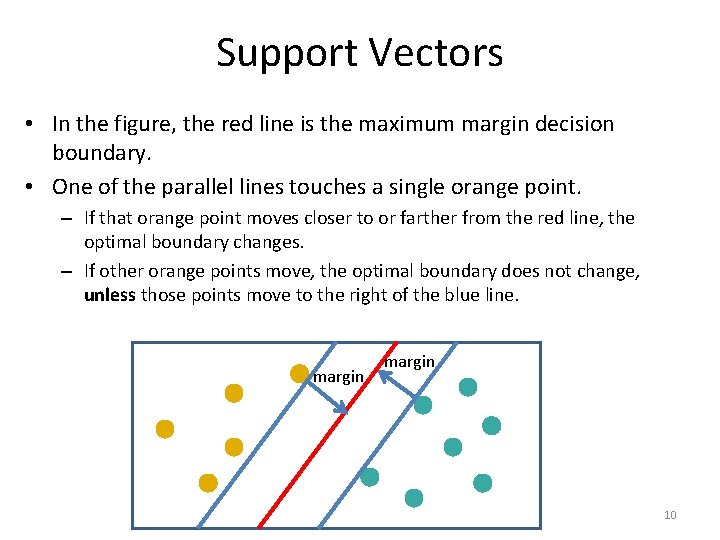
Support Vectors • In the figure, the red line is the maximum margin decision boundary. • One of the parallel lines touches a single orange point. – If that orange point moves closer to or farther from the red line, the optimal boundary changes. – If other orange points move, the optimal boundary does not change, unless those points move to the right of the blue line. margin 10

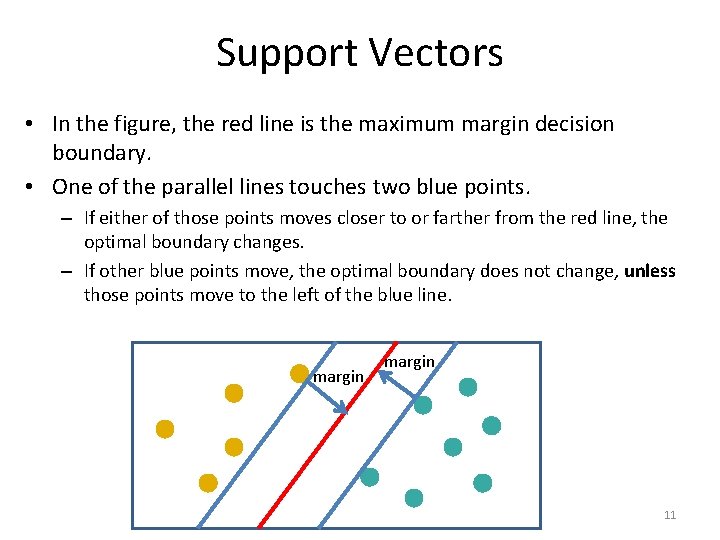
Support Vectors • In the figure, the red line is the maximum margin decision boundary. • One of the parallel lines touches two blue points. – If either of those points moves closer to or farther from the red line, the optimal boundary changes. – If other blue points move, the optimal boundary does not change, unless those points move to the left of the blue line. margin 11

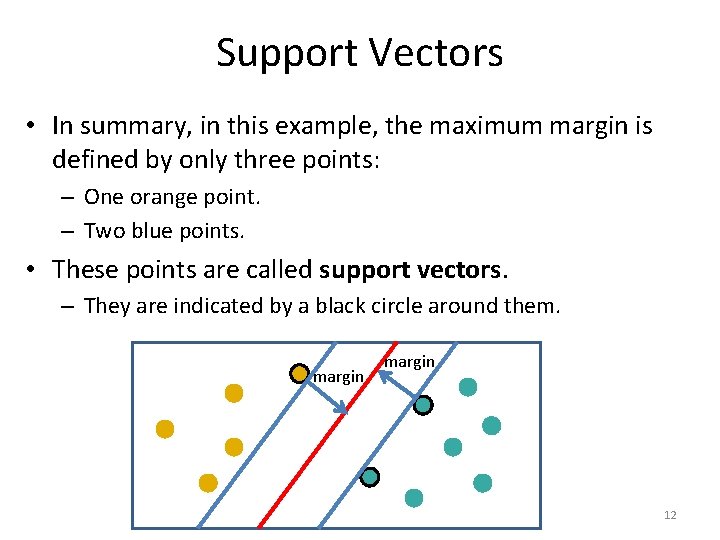
Support Vectors • In summary, in this example, the maximum margin is defined by only three points: – One orange point. – Two blue points. • These points are called support vectors. – They are indicated by a black circle around them. margin 12

Distances to the Boundary • 13

Distances to the Boundary • 14

Distances to the Boundary • 15

Optimization Criterion • 16

Optimization Criterion • 17

Optimization Criterion • 18


Optimization Criterion • These are equivalent formulations. The textbook uses the last one because it simplifies subsequent calculations. 20

Constrained Optimization • 21

Quadratic Programming • Our constrained optimization problem can be solved using a method called quadratic programming. • Describing quadratic programming in depth is outside the scope of this course. • Our goal is simply to understand how to use quadratic programming as a black box, to solve our optimization problem. – This way, you can use any quadratic programming toolkit (Matlab includes one). 22

Quadratic Programming • 23

Quadratic Programming for SVMs • 24

Quadratic Programming for SVMs • 25

Quadratic Programming for SVMs • 26

Quadratic Programming for SVMs • 27

Quadratic Programming for SVMs • 28

Quadratic Programming for SVMs • 29

Quadratic Programming for SVMs • 30

Quadratic Programming for SVMs • 31

Quadratic Programming for SVMs • 32

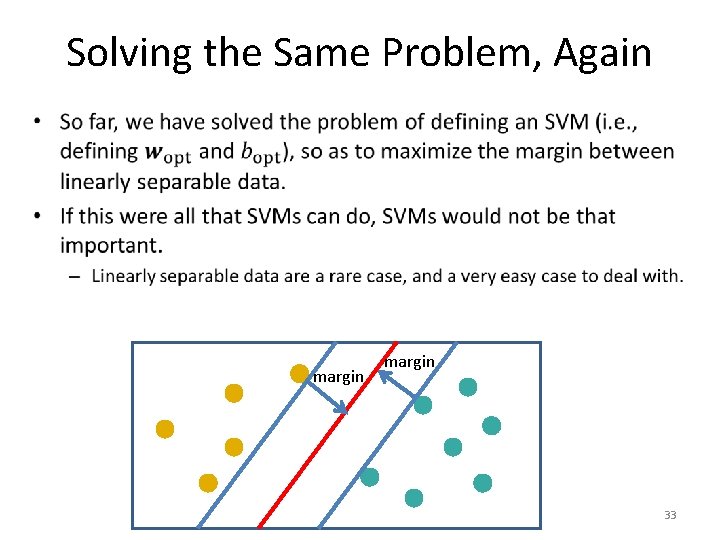
Solving the Same Problem, Again • margin 33

Solving the Same Problem, Again • 34

Lagrange Multipliers • 35

Lagrange Multipliers • 36

Multiple Constraints • 37

Lagrange Dual Problems • 38

Lagrange Dual Problems • 39

Lagrange Multipliers and SVMs • 40

Lagrange Multipliers and SVMs • 41

Lagrange Multipliers and SVMs • 42

Lagrange Multipliers and SVMs • 43

Lagrange Multipliers and SVMs • 44

Lagrange Multipliers and SVMs • We have shown before that the red part equals 0. 45

Lagrange Multipliers and SVMs • 46

Lagrange Multipliers and SVMs • 47

Lagrange Multipliers and SVMs • 48

Lagrange Multipliers and SVMs • 49

SVM Optimization Problem • This problem can be solved again using quadratic programming. 50

Using Quadratic Programming • 51

Using Quadratic Programming • 52

Using Quadratic Programming • 53

Using Quadratic Programming • 54

Using Quadratic Programming • 55

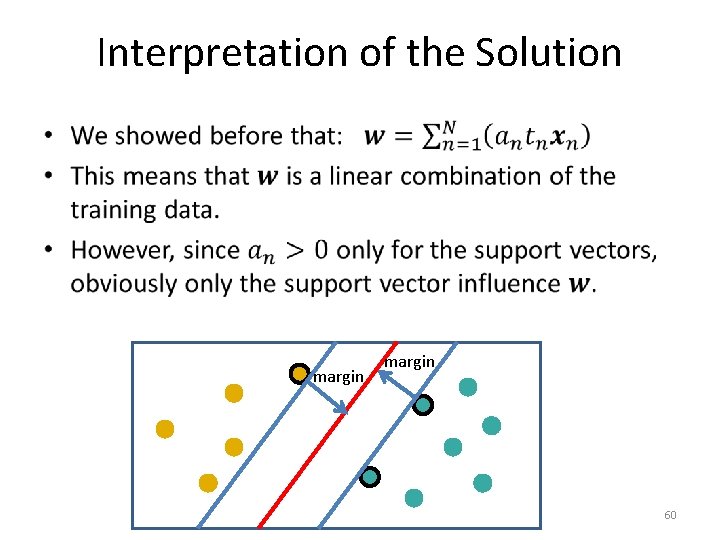
Interpretation of the Solution • 56

Interpretation of the Solution • 57

Interpretation of the Solution • 58

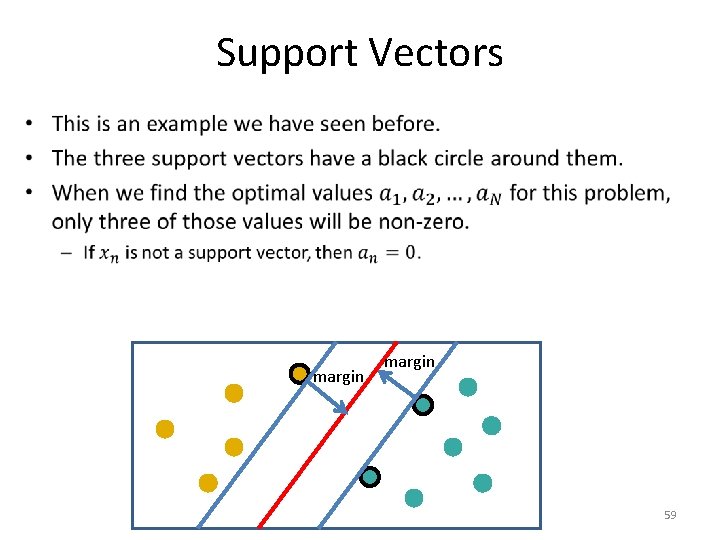
Support Vectors • margin 59

Interpretation of the Solution • margin 60





Recap of Lagrangian-Based Solution • 65

Why Did We Do All This? • The Lagrangian-based solution solves a problem that we had already solved, in a more complicated way. • Typically, we prefer simpler solutions. • However, this more complicated solution can be tweaked relatively easily, to produce more powerful SVMs that: – Can be trained even if the training data is not linearly separable. – Can produce nonlinear decision boundaries. 66

The Not Linearly Separable Case • 67

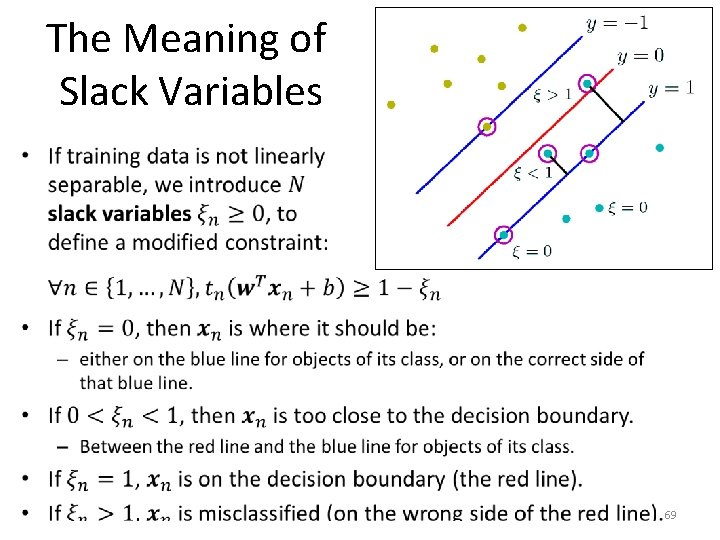
The Meaning of Slack Variables • 68

The Meaning of Slack Variables • 69

Optimization Criterion • 70

Lagrangian Function • 71

Lagrangian Function • 72

Lagrangian Function • 73

Lagrangian Function • 74

Lagrangian Function • 75

Lagrangian Function • 76

Lagrangian Function • 77

Lagrangian Function • 78

Using Quadratic Programming • 79

Using Quadratic Programming • 80

Using Quadratic Programming • 81

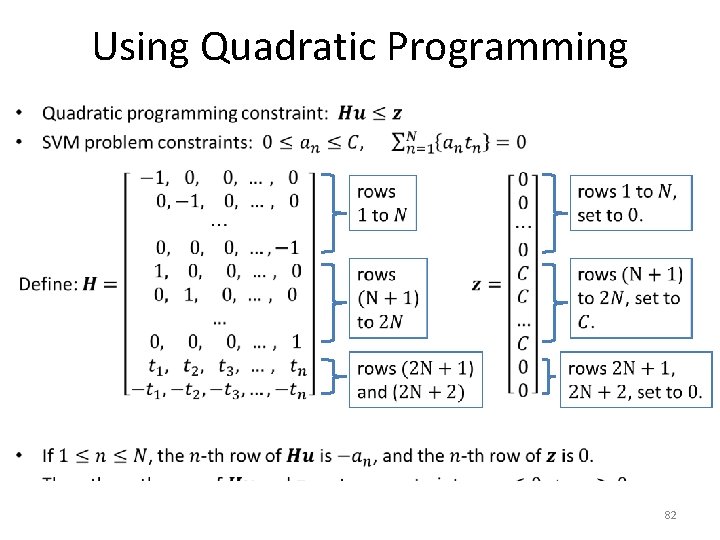
Using Quadratic Programming • 82

Using Quadratic Programming • 83

Using Quadratic Programming • 84

Using Quadratic Programming • 85

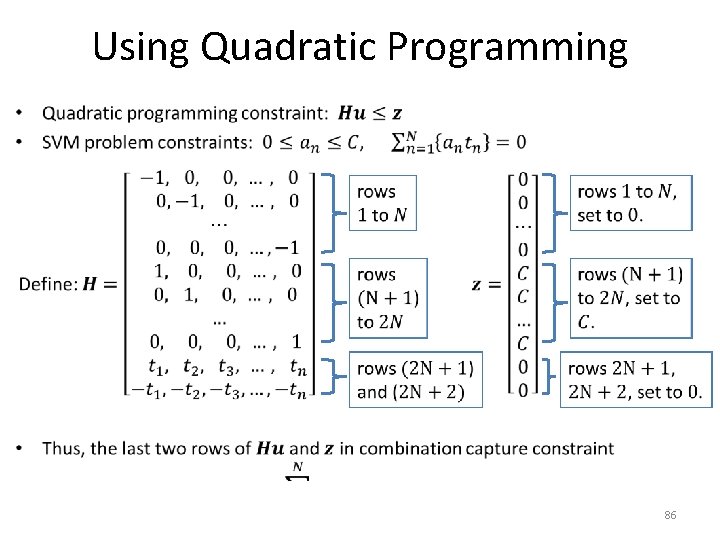
Using Quadratic Programming • 86

Using the Solution • 87


The Role of Training Inputs • 89

The Role of Training Inputs • 90

The Kernel Trick • 91

A Different Kernel • 92

Kernels and Basis Functions • 93

Polynomial Kernels • 94

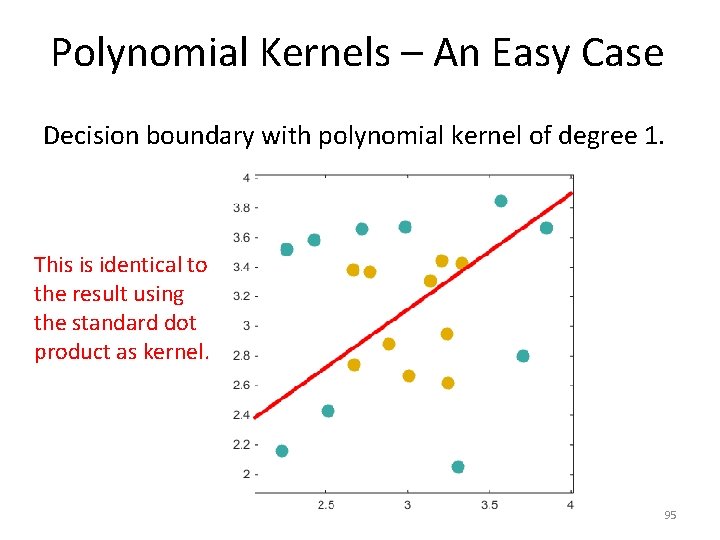
Polynomial Kernels – An Easy Case Decision boundary with polynomial kernel of degree 1. This is identical to the result using the standard dot product as kernel. 95

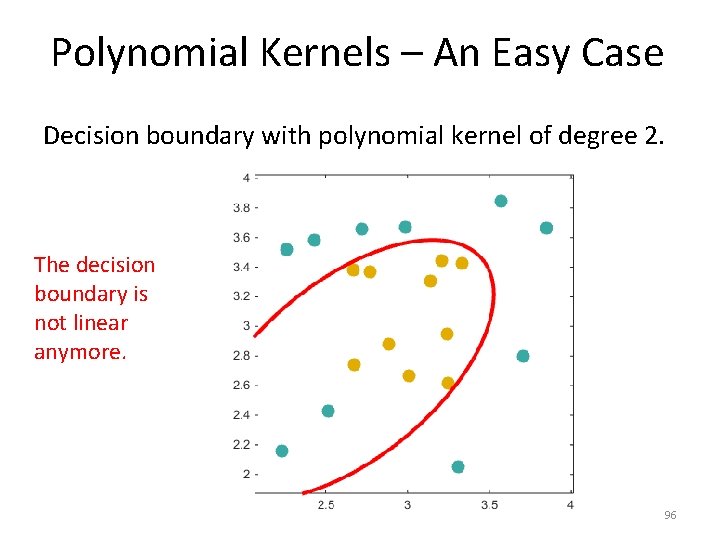
Polynomial Kernels – An Easy Case Decision boundary with polynomial kernel of degree 2. The decision boundary is not linear anymore. 96

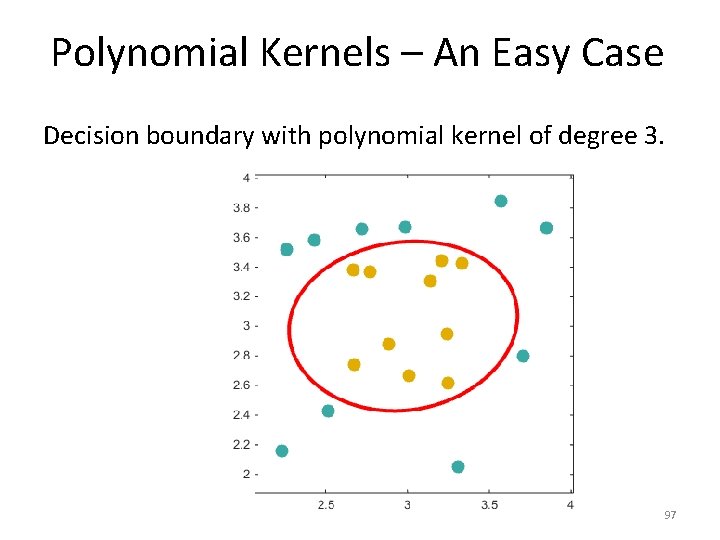
Polynomial Kernels – An Easy Case Decision boundary with polynomial kernel of degree 3. 97

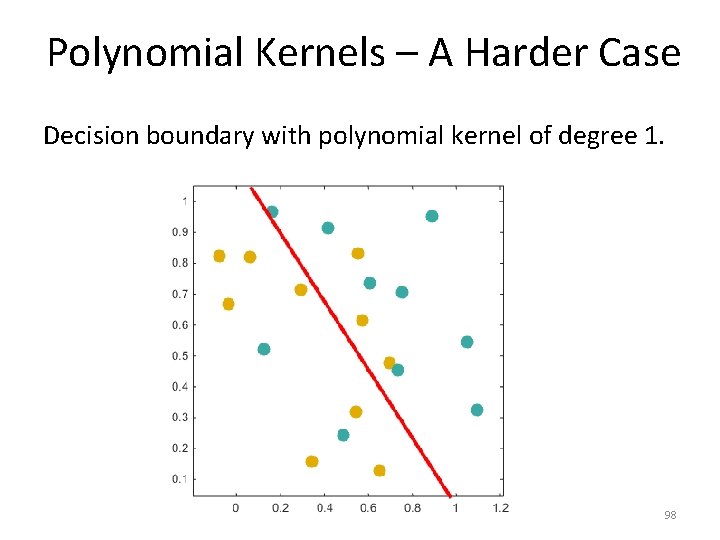
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 1. 98

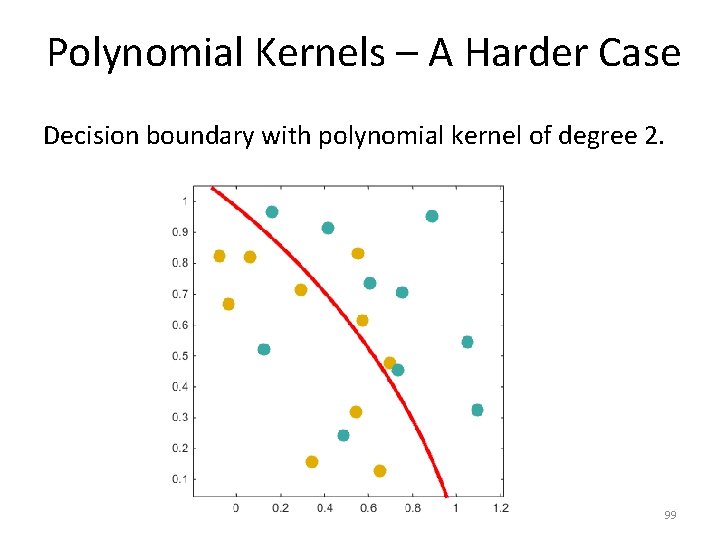
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 2. 99

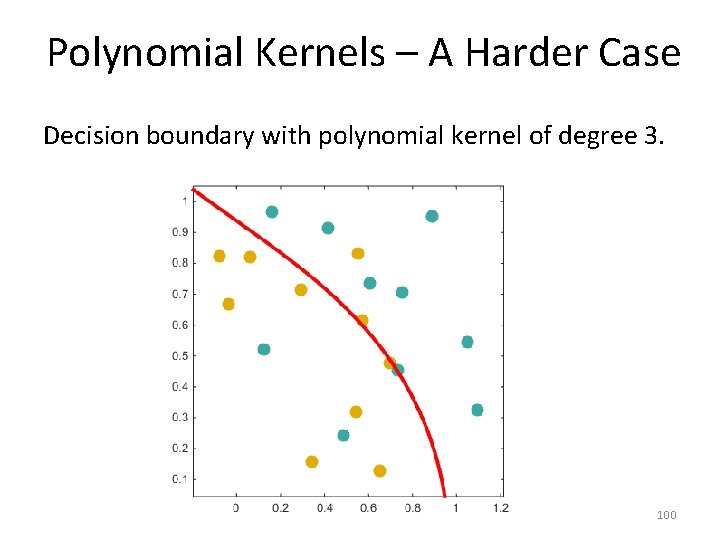
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 3. 100

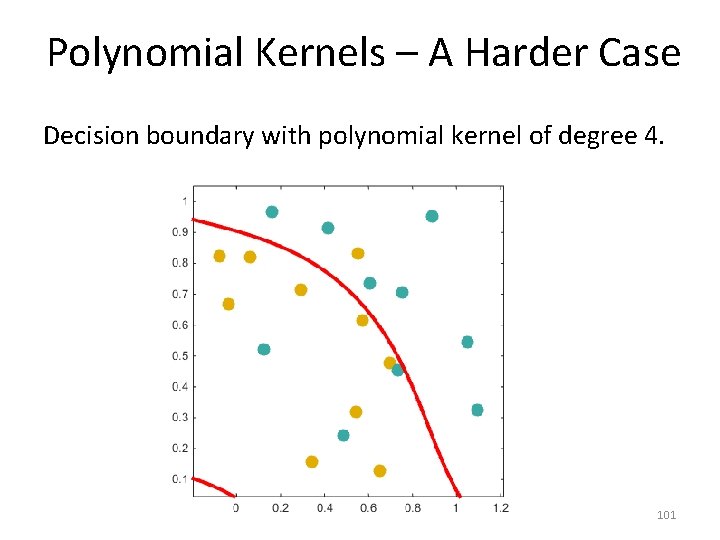
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 4. 101

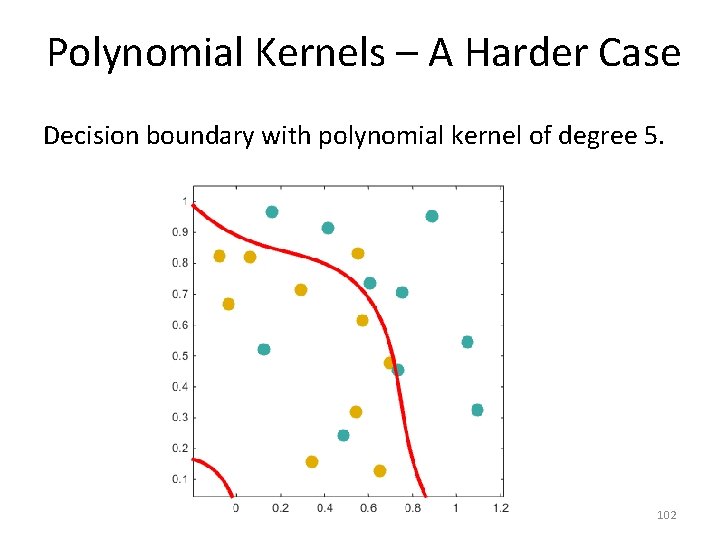
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 5. 102

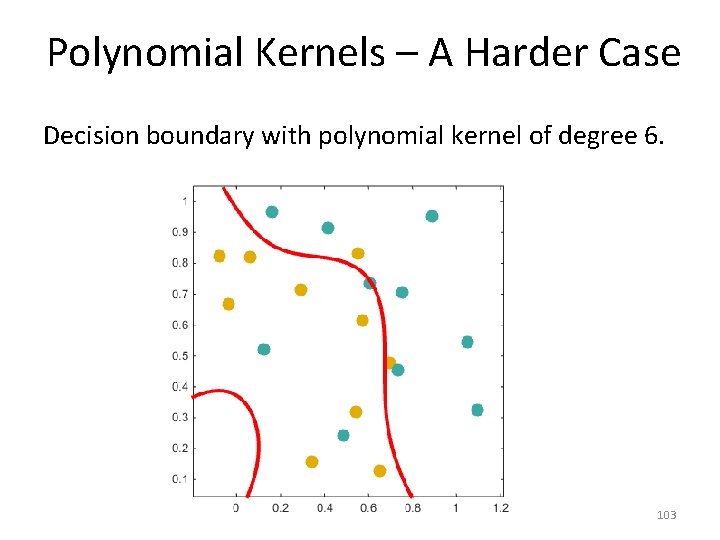
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 6. 103

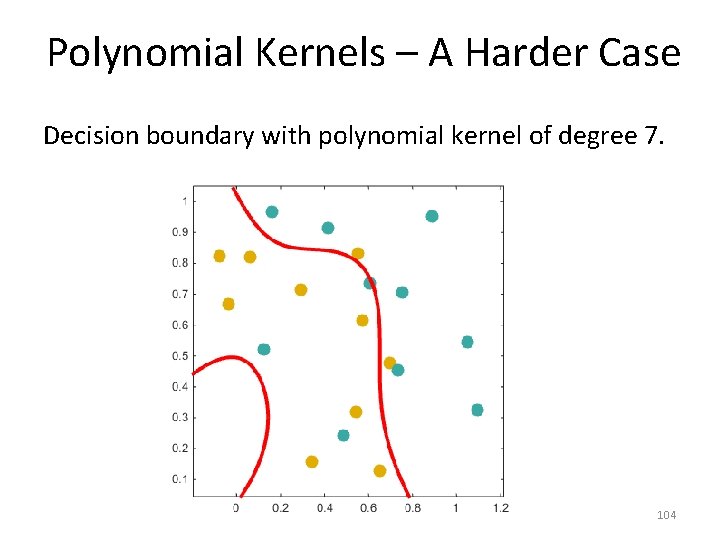
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 7. 104

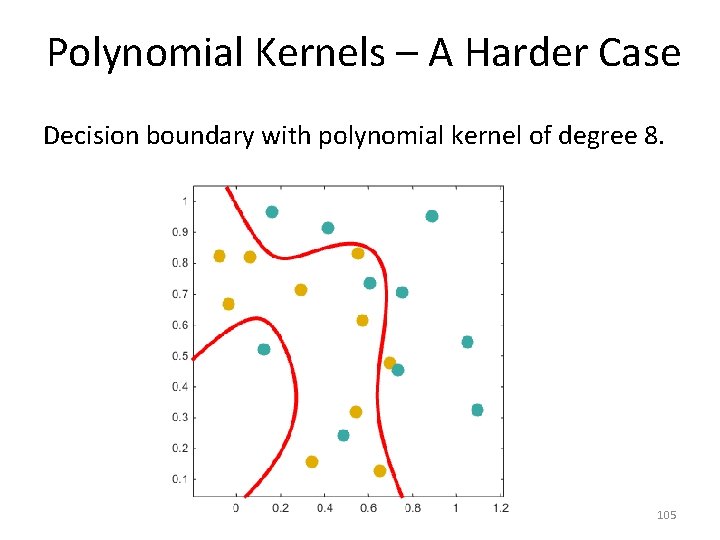
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 8. 105

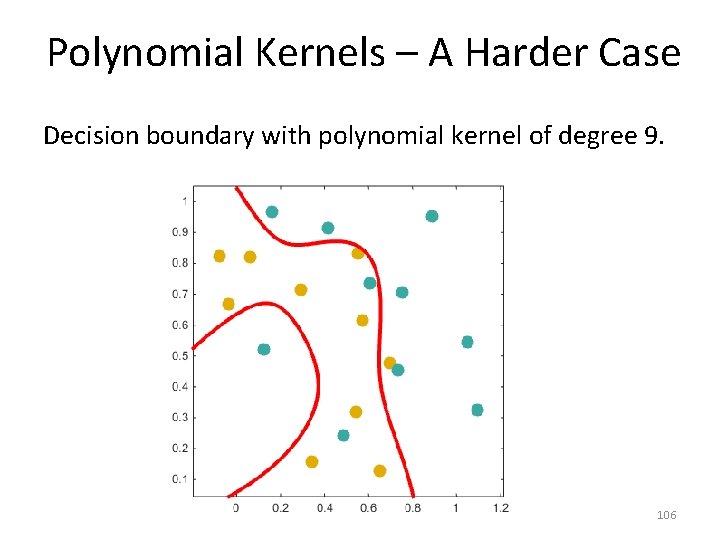
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 9. 106

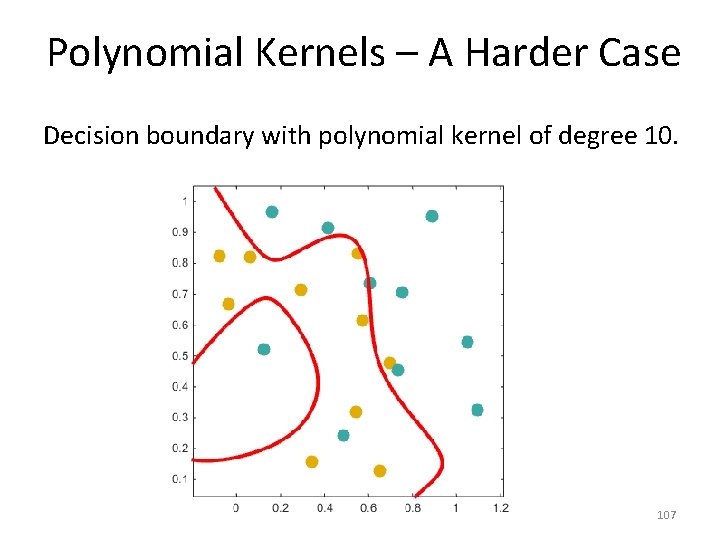
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 10. 107

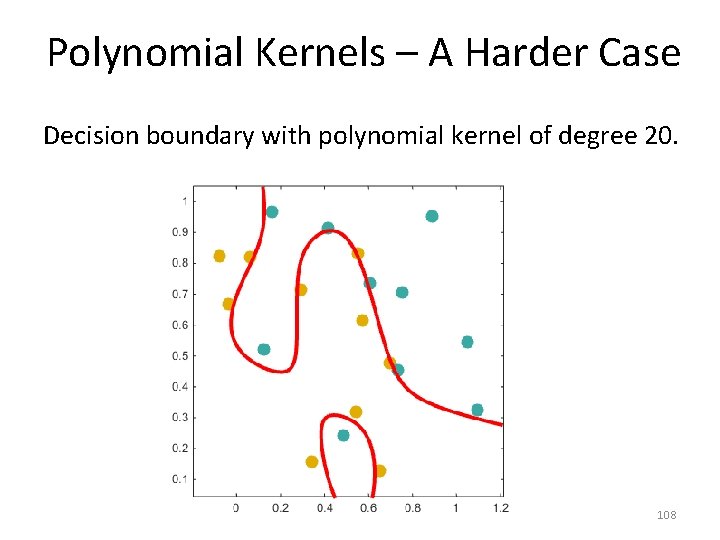
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 20. 108

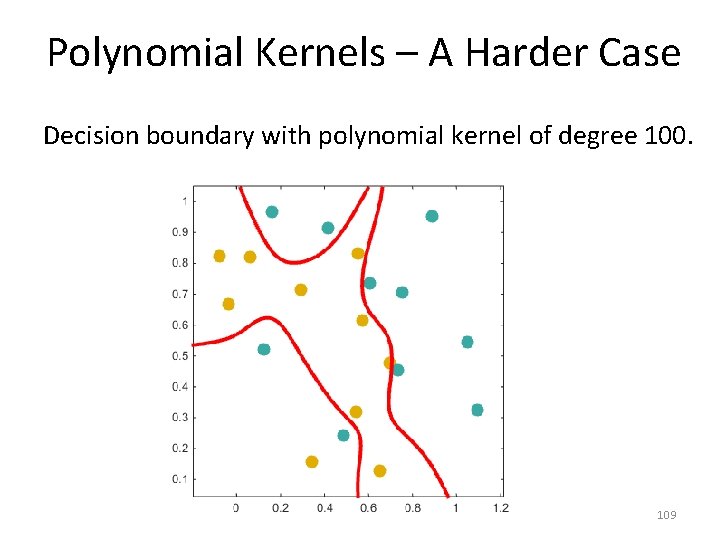
Polynomial Kernels – A Harder Case Decision boundary with polynomial kernel of degree 100. 109

RBF/Gaussian Kernels • 110

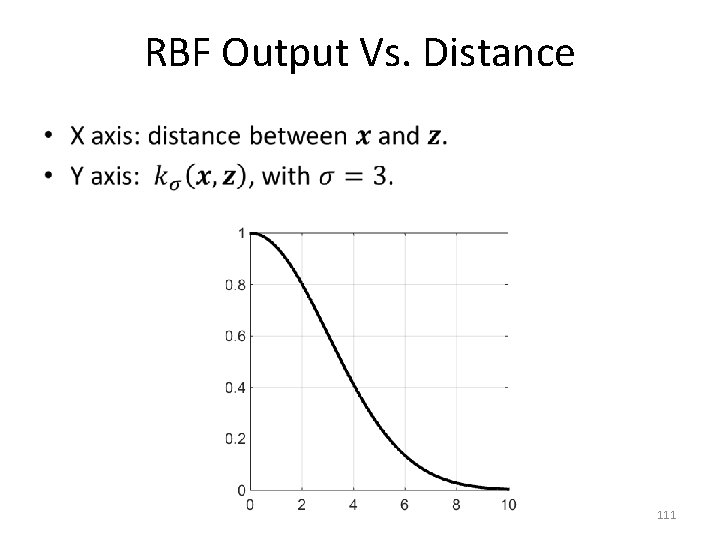
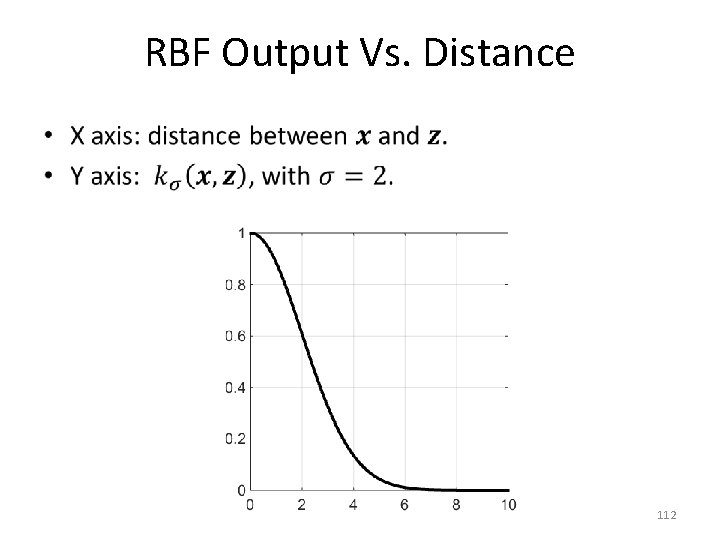
RBF Output Vs. Distance • 111

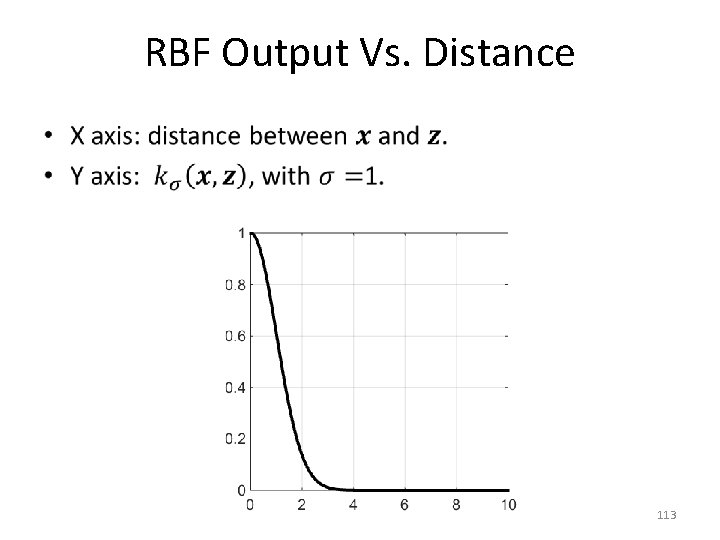
RBF Output Vs. Distance • 112

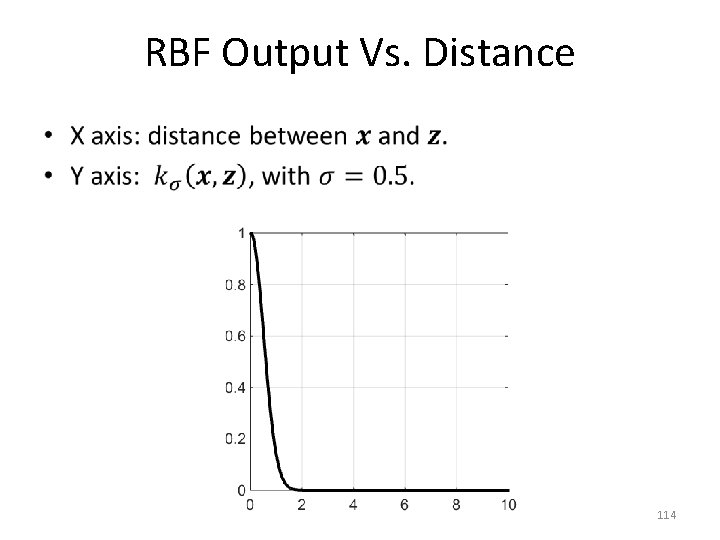
RBF Output Vs. Distance • 113

RBF Output Vs. Distance • 114

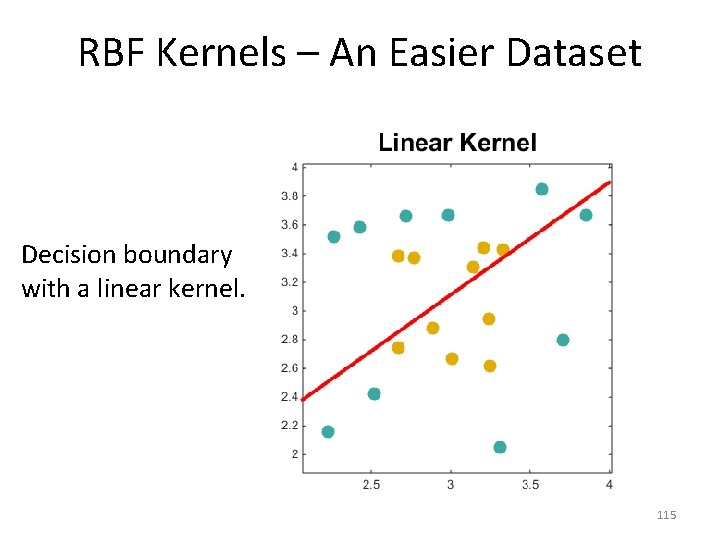
RBF Kernels – An Easier Dataset Decision boundary with a linear kernel. 115

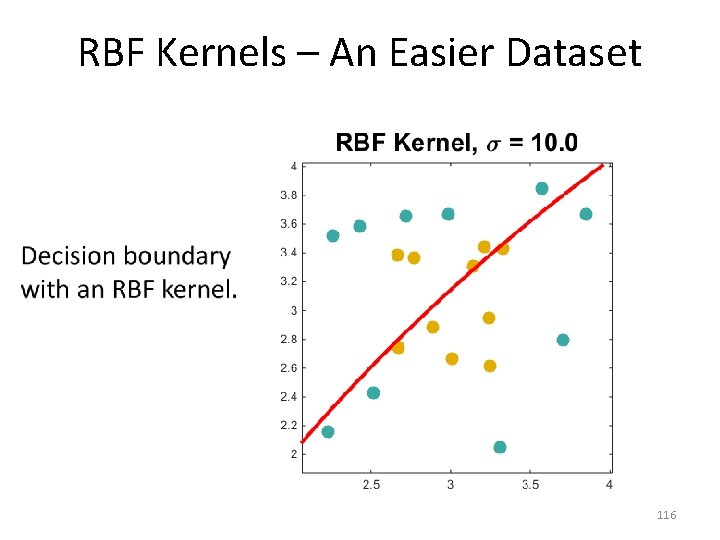
RBF Kernels – An Easier Dataset • 116

RBF Kernels – An Easier Dataset • 117

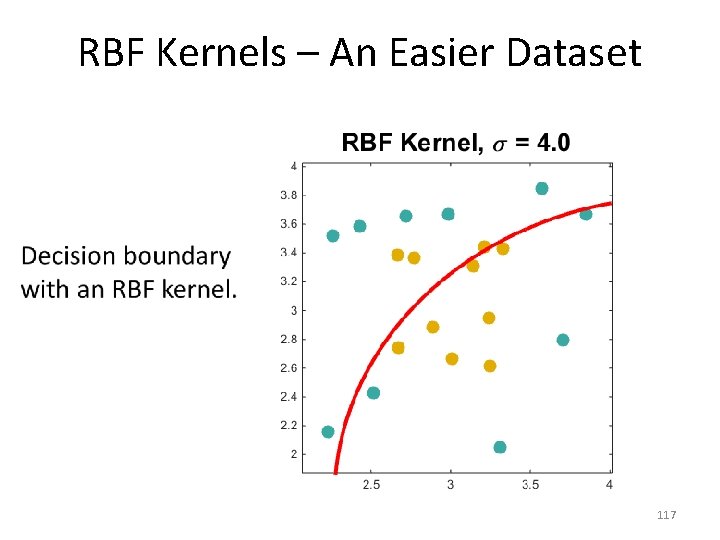
RBF Kernels – An Easier Dataset • 118

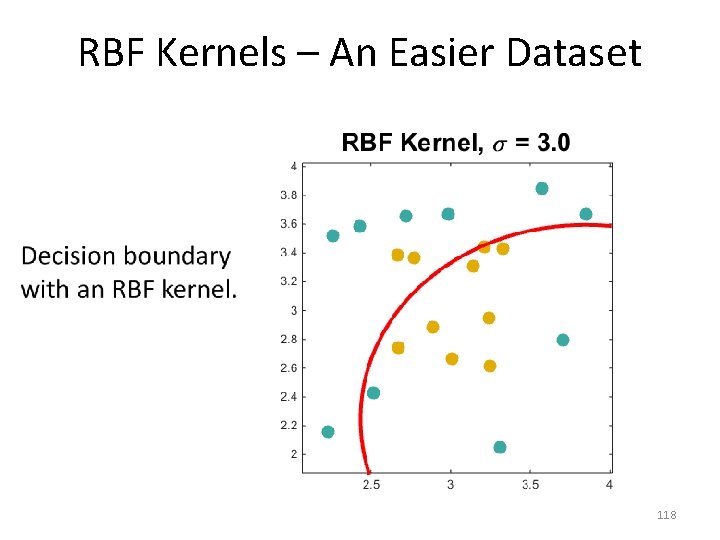
RBF Kernels – An Easier Dataset • 119

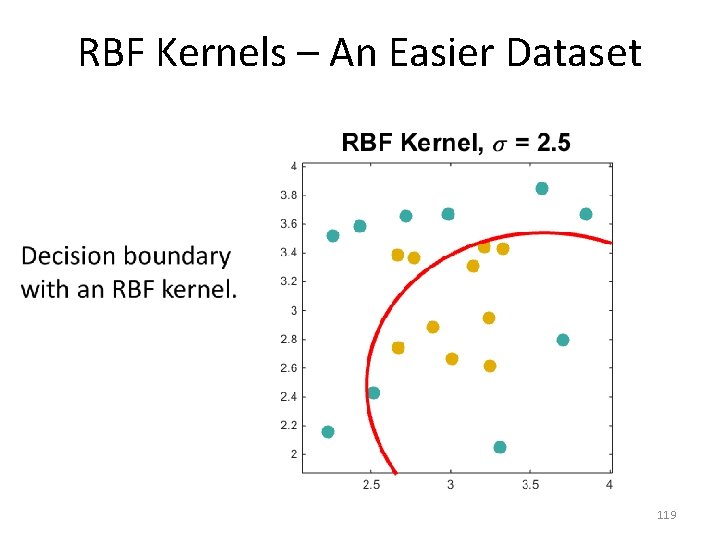
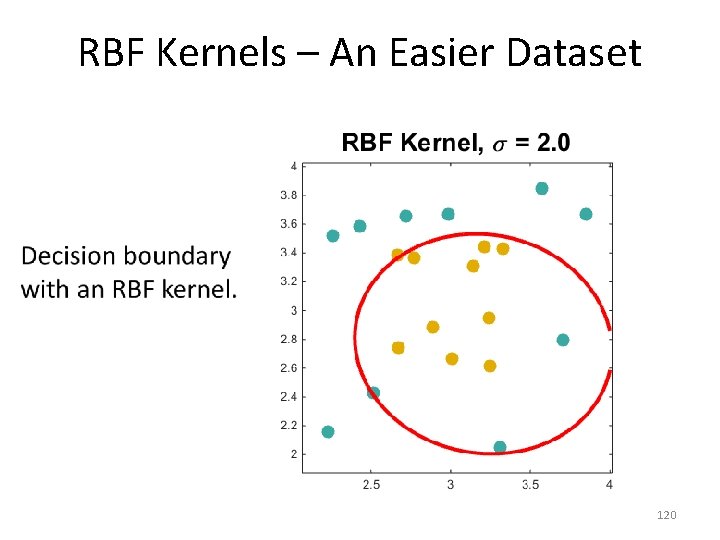
RBF Kernels – An Easier Dataset • 120

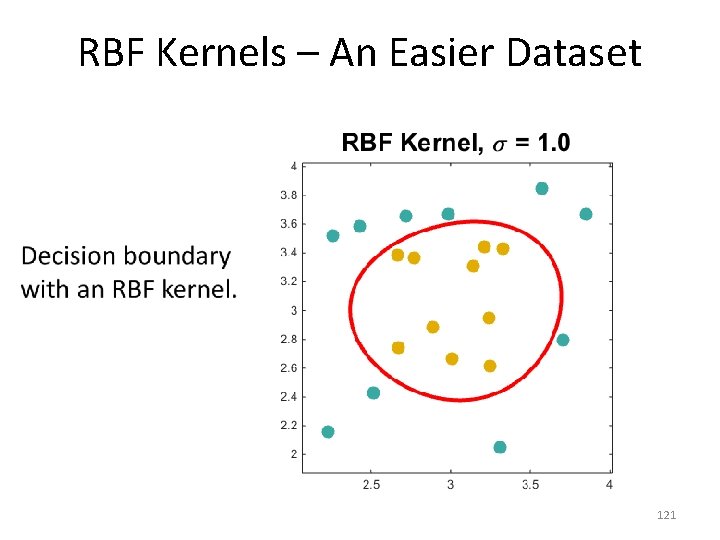
RBF Kernels – An Easier Dataset • 121

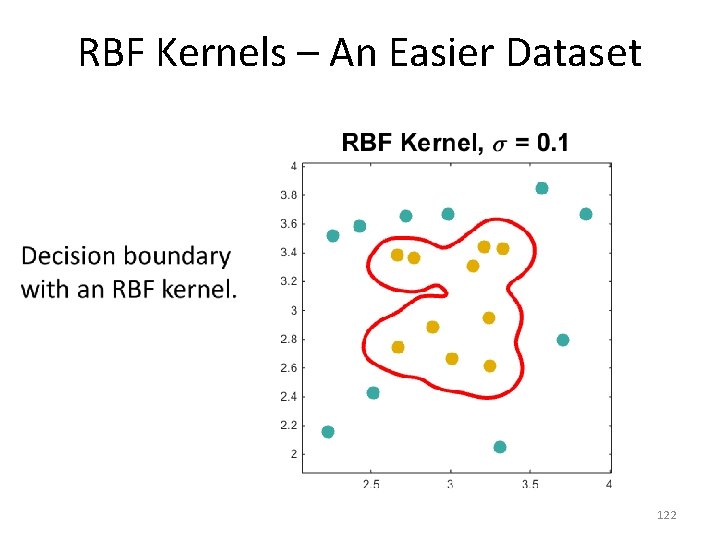
RBF Kernels – An Easier Dataset • 122

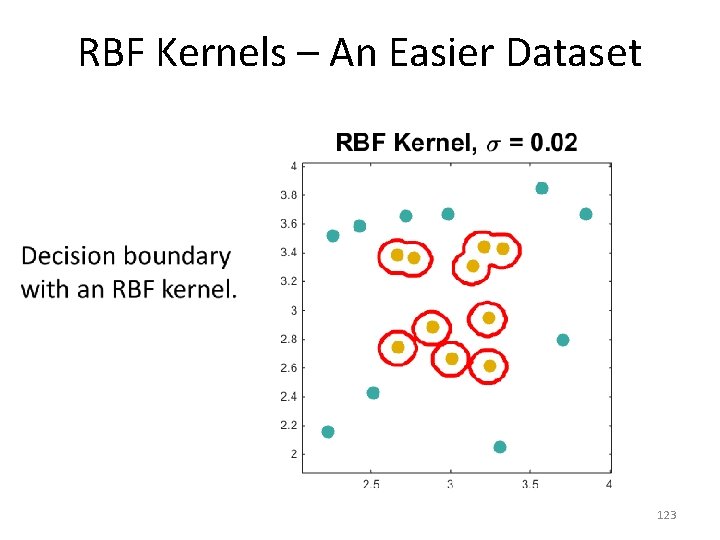
RBF Kernels – An Easier Dataset • 123

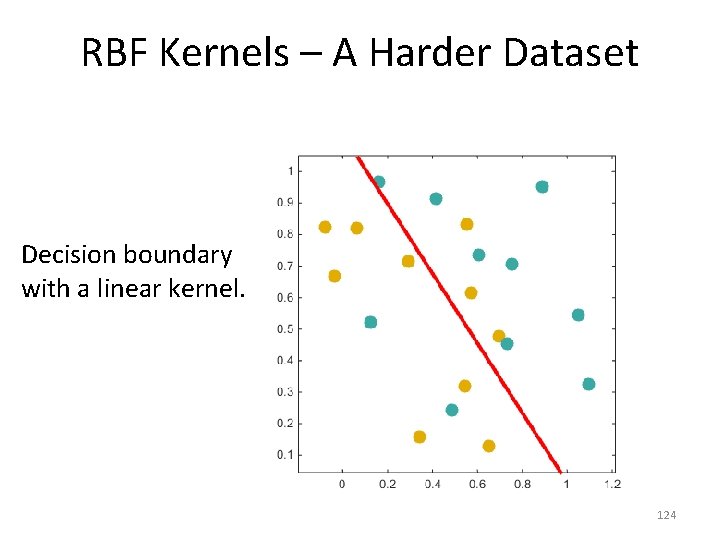
RBF Kernels – A Harder Dataset Decision boundary with a linear kernel. 124

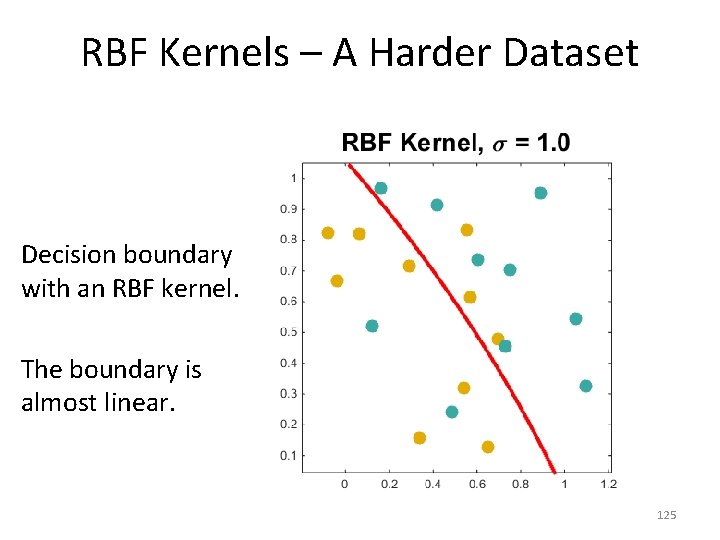
RBF Kernels – A Harder Dataset Decision boundary with an RBF kernel. The boundary is almost linear. 125

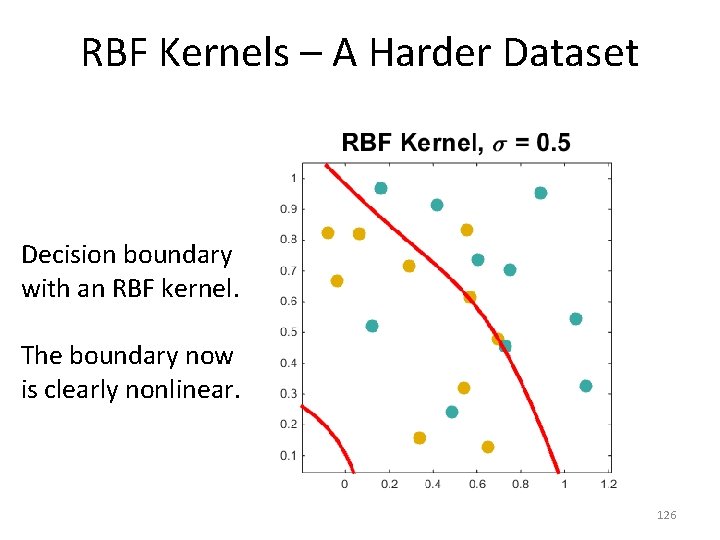
RBF Kernels – A Harder Dataset Decision boundary with an RBF kernel. The boundary now is clearly nonlinear. 126

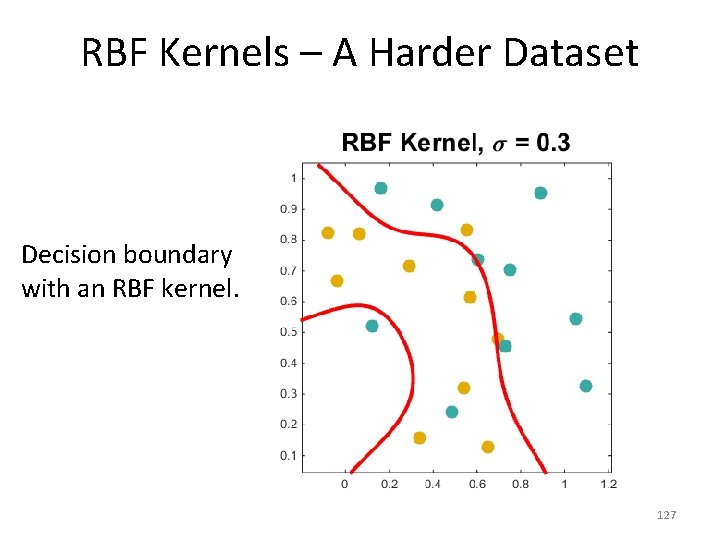
RBF Kernels – A Harder Dataset Decision boundary with an RBF kernel. 127

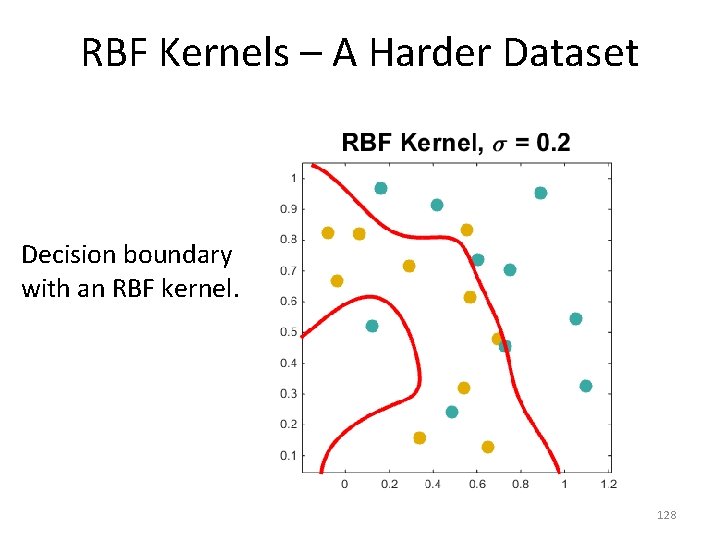
RBF Kernels – A Harder Dataset Decision boundary with an RBF kernel. 128

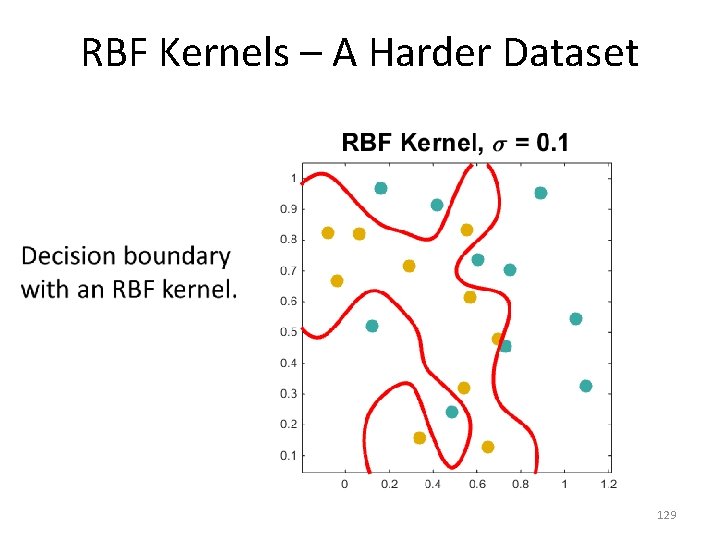
RBF Kernels – A Harder Dataset • 129

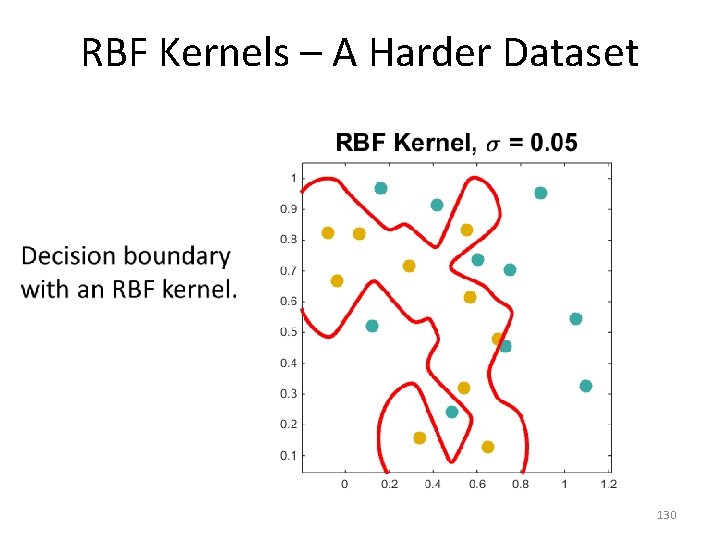
RBF Kernels – A Harder Dataset • 130

RBF Kernels and Basis Functions • 131

Kernels for Non-Vector Data • 132

Kernels for Non-Vector Data • 133

Training Time Complexity • 134

Training Time Complexity • 135

SVMs for Multiclass Problems • As usual, you can always train one-vs. -all SVMs if there are more than two classes. • Other, more complicated methods are also available. • You can also train what is called "all-pairs" classifiers: – Each SVM is trained to discriminate between two classes. – The number of SVMs is quadratic to the number of classes. • All-pairs classifiers can be used in different ways to classify an input object. – Each pairwise classifier votes for one of the two classes it was trained on. Classification time is quadratic to the number of classes. – There is an alternative method, called DAGSVM, where the all-pairs classifiers are organized in a directed acyclic graph, and classification time is linear to the number of classes. 136

SVMs: Recap • 137