Support Vector Machines and The Kernel Trick William




















![The kernel trick – con’t x=“william” j={1, 3, 4} x[j]=“wll”<“wl” len(x, j)=4 Kernels work The kernel trick – con’t x=“william” j={1, 3, 4} x[j]=“wll”<“wl” len(x, j)=4 Kernels work](https://slidetodoc.com/presentation_image_h/a83a61b1cdff1a516a4b24a5f2cdd02c/image-23.jpg)








- Slides: 31

Support Vector Machines and The Kernel Trick William Cohen 3 -26 -2007

The voted perceptron A instance xi B ^ yi yi ^ Compute: yi = vk. xi If mistake: vk+1 = vk + yi xi

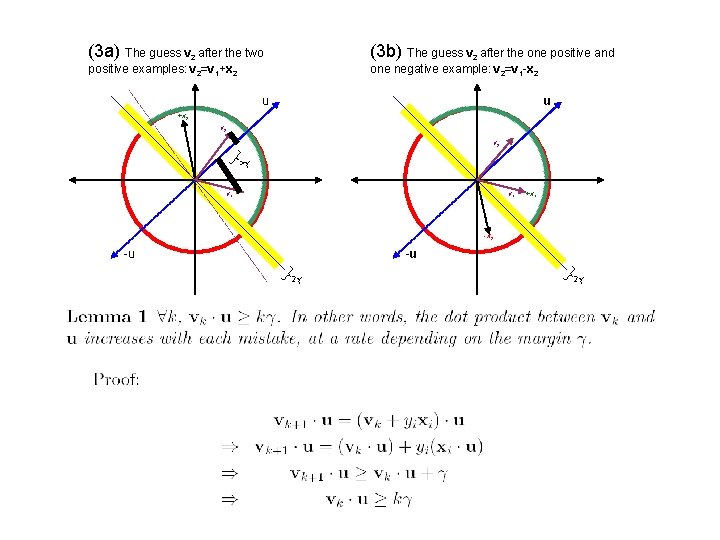
(3 a) The guess v 2 after the two (3 b) The guess v 2 after the one positive and positive examples: v 2=v 1+x 2 one negative example: v 2=v 1 -x 2 u u +x 2 v 2 >γ v 1 +x 1 -x 2 -u -u 2γ 2γ


Perceptrons vs SVMs • For the voted perceptron to “work” (in this proof), we need to assume there is some u such that . . or, u. u=||u||2=1

Perceptrons vs SVMs • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: γ, (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Find: some w where • ||w||2=1 and • for all i, w. xi. yi > γ

Perceptrons vs SVMs • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Find: some w and γ such that • ||w||=1 and • for all i, w. xi. yi > γ The best possible w and γ

Perceptrons vs SVMs • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Maximize γ under the constraint • ||w||2=1 and • for all i, w. xi. yi > γ – Mimimize ||w||2 under the constraint • for all i, w. xi. yi > 1 Units are arbitrary: rescaling increases γ and w

SVMs and optimization • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Find: objective function …but here nothing is linear, so you need to use quadratic programming This is a constrained optimization problem. constraints Famous example of constrained optimization: linear programming, where objective function is linear, constraints are linear (in)equalities

SVMs and optimization • Motivation for SVMs as “better perceptrons” – learners that minimize w. w under the constraint that for all i, yiw. xi>1 • Questions: – What if the data isn’t separable? • Slack variables • Kernel trick – How do you solve this constrained optimization problem?

SVMs and optimization • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Find:

SVM with slack variables http: //www. csie. ntu. edu. tw/~cjlin/libsvm/

The Kernel Trick

The voted perceptron A instance xi B ^ yi yi ^ Compute: yi = vk. xi If mistake: vk+1 = vk + yi xi

The kernel trick Remember: sparse weighted sum of examples where i 1, …, ik are the mistakes… so: Can think of this as a weighted sum of all examples with some of the weights being zero – non-zero weighted examples are support vectors

The kernel trick – con’t Since: where i 1, …, ik are the mistakes… then Consider a preprocesser that replaces every x with x’ to include, directly in the example, all the pairwise variable interactions, so what is learned is a vector v’:

The kernel trick – con’t A voted perceptron over vectors like u, v is a linear function… Replacing u with u’ would lead to non -linear functions – f(x, y, x 2, …)

The kernel trick – con’t But notice…if we replace uv with (uv+1)2 …. Compare to

The kernel trick – con’t So – up to constants on the cross-product terms Why not replace the computation of With the computation of where ?

The kernel trick – con’t General idea: replace an expensive preprocessor x x’ and ordinary inner product with no preprocessor and a function K(x, xi) where Some popular kernels for numeric vectors x:

Demo with An Applet http: //www. site. uottawa. ca/~gcaron/SVMApplet. html

The kernel trick – con’t Kernels work for other data structures also! • String kernels: • x and xi are strings, S=set of shared substrings, |s|=length of string s: by dynamic programming you can quickly compute There also tree kernels, graph kernels, …. .
![The kernel trick cont xwilliam j1 3 4 xjwllwl lenx j4 Kernels work The kernel trick – con’t x=“william” j={1, 3, 4} x[j]=“wll”<“wl” len(x, j)=4 Kernels work](https://slidetodoc.com/presentation_image_h/a83a61b1cdff1a516a4b24a5f2cdd02c/image-23.jpg)
The kernel trick – con’t x=“william” j={1, 3, 4} x[j]=“wll”<“wl” len(x, j)=4 Kernels work for other data structures also! • String kernels: • x and xi are strings, S=set of shared substrings, j, k are subsets of the positions inside x, xi, len(x, j) is the distance between the first position in j and the last, s<t means s is a substring of t, by dynamic programming you can quickly compute

The kernel trick – con’t Even more general idea: use any function K that is • Continuous • Symmetric—i. e. , K(u, v)=K(v, u) • “Positive semidefinite”—i. e. , K(u, v)≥ 0 Then by an ancient theorem due to Mercer, K corresponds to some combination of a preprocessor and an inner product: i. e. , Terminology: K is a Mercer kernel. The set of all x’ is a reproducing kernel Hilbert space (RKHS). The matrix M[i, j]=K(xi, xj) is a Gram matrix.

SVMs and optimization • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Find: primal form which is equivalent to finding: Lagrangian dual

Langrange multipliers maximize f(x, y)=2 -x 2 -2 y 2 subject to g(x)=x 2+y 2 -1=0

Langrange multipliers maximize f(x, y)=2 -x 2 -2 y 2 subject to g(x)=x 2+y 2 -1=0 Claim: at the constrained maximum the gradient of f must be perpendicular to g

Langrange multipliers maximize f(x, y)=2 -x 2 -2 y 2 subject to g(x)=x 2+y 2 -1=0 Claim: at the constrained maximum the gradient of f must be perpendicular to g

SVMs and optimization • Question: why not use this assumption directly in the learning algorithm? i. e. – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … – Find: primal form which is equivalent to finding: Lagrangian dual

SVMs and optimization • Question: why not use this assumption directly in the learning algorithm? i. e. Some key points: – Given: (x 1, y 1), (x 2, y 2), (x 3, y 3), … • Solving the QP directly (Vapnik’s – Find: original method) is possible but expensive. • The dual form can be expressed as constraints on each example • eg. αi=0 yiw. xi≥ 1 KKT (Karush-Kuhn-Tucker) conditions or Kuhn-Tucker conditions, after Karush (1939) and Kuhn-Tucker (1951) • Fastest methods for SVM learning ignore most of the constraints, solve a subproblem containing a few ‘active constraints’, then cleverly pick a few additional constraints & repeat…. .

More on SVMs and kernels • Many other types of algorithms can be “kernelized” – Gaussian processes, memory-based/nearest neighbor methods, …. • Work on optimization for linear SVMs is very active