Support Vector Machines 1 Introduction to SVMs 2

Support Vector Machines 1. Introduction to SVMs 2. Linear SVMs 3. Non-linear SVMs References: 1. S. Y. Kung, M. W. Mak, and S. H. Lin. Biometric Authentication: A Machine Learning Approach, Prentice Hall, to appear. 2. S. R. Gunn, 1998. Support Vector Machines for Classification and Regression. (http: //www. isis. ecs. soton. ac. uk/resources/svminfo/) 3. Bernhard Schölkopf. Statistical learning and kernel methods. MSR-TR 2000 -23, Microsoft Research, 2000. (ftp: //ftp. research. microsoft. com/pub/tr/tr-2000 -23. pdf) 4. For more resources on support vector machines, see http: //www. kernel-machines. org/ 11/1/2020 Support Vector Machines M. W. Mak 1

Introduction l l SVMs were developed by Vapnik in 1995 and are becoming popular due to their attractive features and promising performance. Conventional neural networks are based on empirical risk minimization where network weights are determined by minimizing the mean squares error between the actual outputs and the desired outputs. SVMs are based on the structural risk minimization principle where parameters are optimized by minimizing classification error. SVMs have been shown to posses better generalization capability than conventional neural networks. 11/1/2020 Support Vector Machines M. W. Mak 2

Introduction (Cont. ) l Given N labeled empirical data: (1) where X is the set of input data in and yi are the labels. Domain X 11/1/2020 Support Vector Machines M. W. Mak 3

Introduction (Cont. ) l We construct a simple classifier by computing the means of the two classes (2) where N 1 and N 2 are the number of data in the class with positive and negative labels, respectively. l l We assign a new point x to the class whose mean is closer to it. To achieve this, we compute 11/1/2020 Support Vector Machines M. W. Mak 4

Introduction (Cont. ) l Then, we determine the class of x by checking whether the vector connecting x and c encloses an angle smaller than /2 with the vector Domain X where x 11/1/2020 Support Vector Machines M. W. Mak 5

Introduction (Cont. ) l In the special case where b = 0, we have (3) l This means that we use ALL data point xi, each being weighted equally by 1/N 1 or 1/N 2, to define the decision plane. 11/1/2020 Support Vector Machines M. W. Mak 6

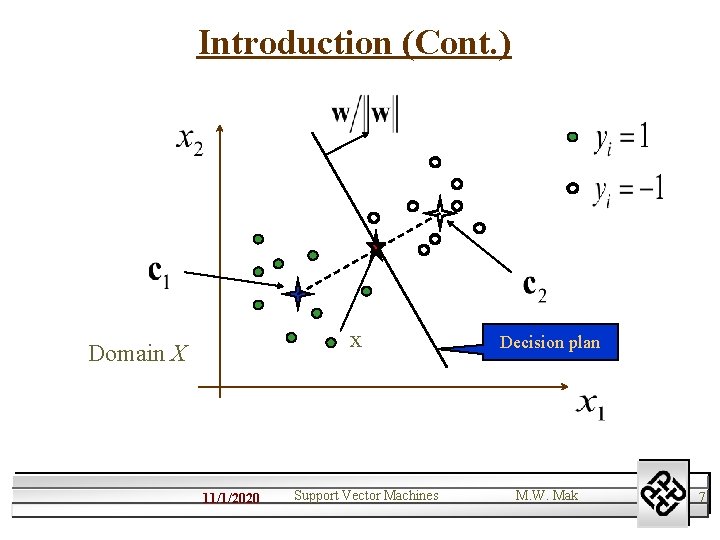
Introduction (Cont. ) x Domain X 11/1/2020 Support Vector Machines Decision plan M. W. Mak 7

Introduction (Cont. ) l l l However, we might want to remove the influence of patterns that are far away from the decision boundary, because their influence is usually small. We may also select only a few important data point (called support vectors) and weight them differently. Then, we have a support vector machine. 11/1/2020 Support Vector Machines M. W. Mak 8

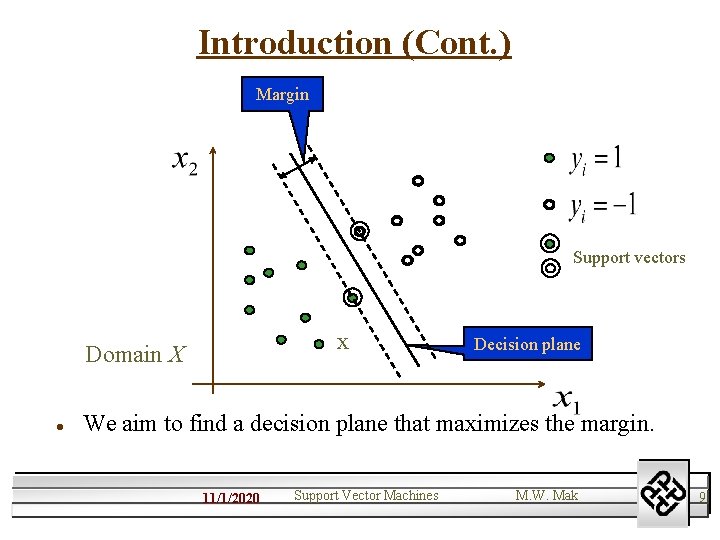
Introduction (Cont. ) Margin Support vectors x Domain X l Decision plane We aim to find a decision plane that maximizes the margin. 11/1/2020 Support Vector Machines M. W. Mak 9

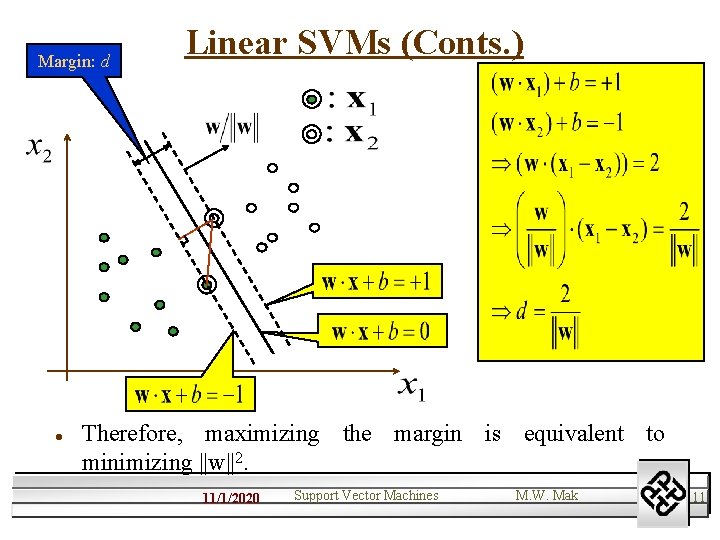
Linear SVMs l Assume that all training data satisfy the constraints: (4) which means (5) l Training data points for which the above equality holds lie on hyperplanes parallel to the decision plane. 11/1/2020 Support Vector Machines M. W. Mak 10

Margin: d l Linear SVMs (Conts. ) Therefore, maximizing the margin is equivalent to minimizing ||w||2. 11/1/2020 Support Vector Machines M. W. Mak 11

Linear SVMs (Lagrangian) l We minimize ||w||2 subject to the constraint that (6) l This can be achieved by introducing Lagrange multipliers and a Lagrangian (7) l The Lagrangian has to be minimized with respect to w and b and maximized with respect to 11/1/2020 Support Vector Machines M. W. Mak 12

Linear SVMs (Lagrangian) l l Setting We obtain (8) l Patterns for which are called Support Vectors. These vectors lie on the margin and satisfy where S contains the indexes to the support vectors. l Patterns for which the classification. 11/1/2020 are considered to be irrelevant to Support Vector Machines M. W. Mak 13

Linear SVMs (Wolfe Dual) l Substituting (8) into (7), we obtain the Wolfe dual: (9) l The hyper-decision plane is thus 11/1/2020 Support Vector Machines M. W. Mak 14

Linear SVMs (Example) l l Analytical example (3 -point problem): Objective function: 11/1/2020 Support Vector Machines M. W. Mak 15

Linear SVMs (Example) l l We introduce another Lagrange multiplier λ to obtain the Lagrangian Differentiating F(α, λ) with respect to λ and αi and set the results to zero, we obtain 11/1/2020 Support Vector Machines M. W. Mak 16

Linear SVMs (Example) l Substitute the Lagrange multipliers into Eq. 8 11/1/2020 Support Vector Machines M. W. Mak 17

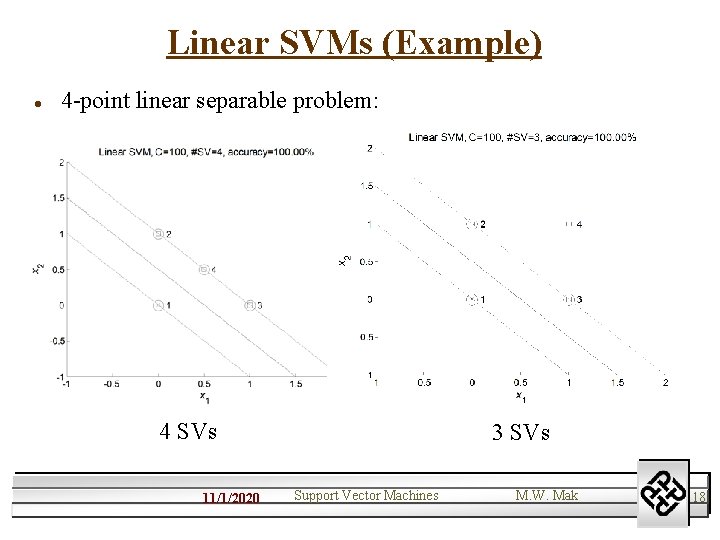
Linear SVMs (Example) l 4 -point linear separable problem: 4 SVs 11/1/2020 3 SVs Support Vector Machines M. W. Mak 18

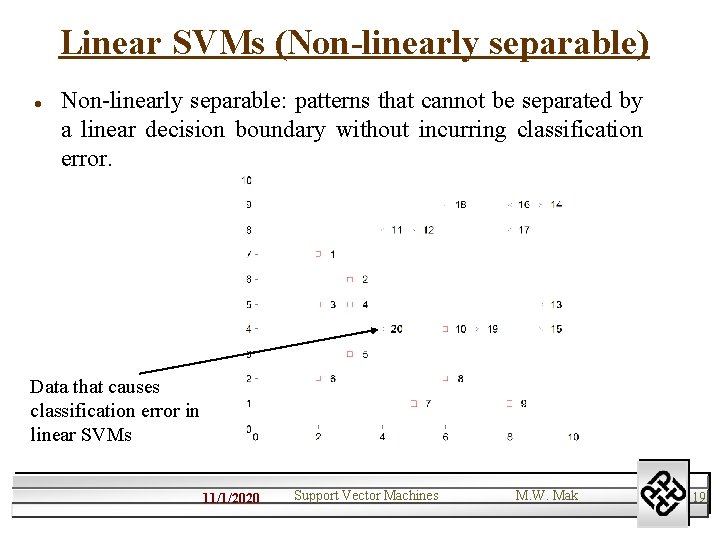
Linear SVMs (Non-linearly separable) l Non-linearly separable: patterns that cannot be separated by a linear decision boundary without incurring classification error. Data that causes classification error in linear SVMs 11/1/2020 Support Vector Machines M. W. Mak 19

Linear SVMs (Non-linearly separable) We introduce a set of slack variables l l l with The slack variables allow some data to violate the constraints defined for the linearly separable case (Eq. 6): Therefore, for some 11/1/2020 we have Support Vector Machines M. W. Mak 20

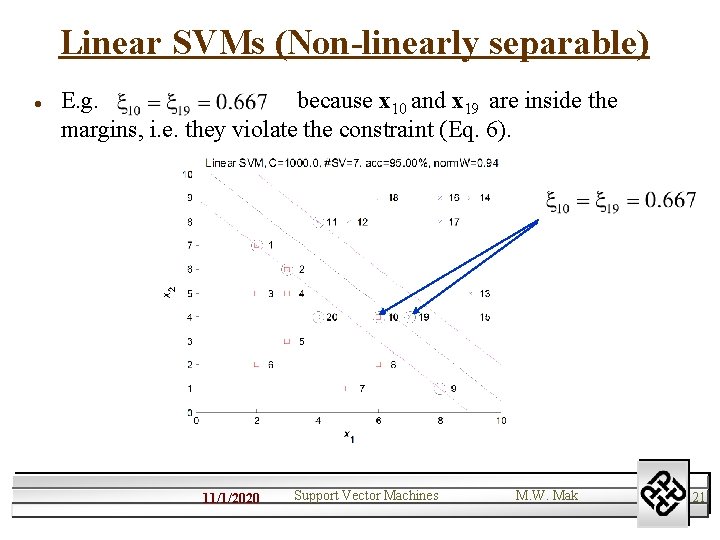
Linear SVMs (Non-linearly separable) l E. g. because x 10 and x 19 are inside the margins, i. e. they violate the constraint (Eq. 6). 11/1/2020 Support Vector Machines M. W. Mak 21

Linear SVMs (Non-linearly separable) l For non-separable cases: where C is a user-defined penalty parameter to penalize any violation of the margins. l The Lagrangian becomes 11/1/2020 Support Vector Machines M. W. Mak 22

Linear SVMs (Non-linearly separable) l l Wolfe dual optimization: The output weight vector and bias term are 11/1/2020 Support Vector Machines M. W. Mak 23

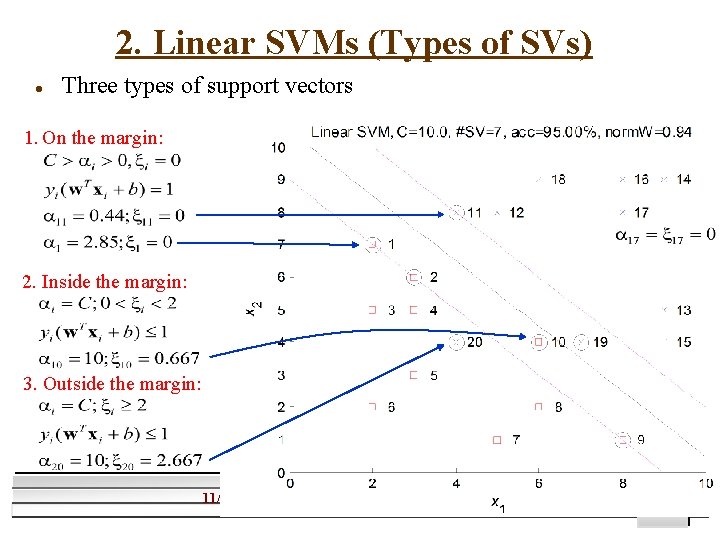
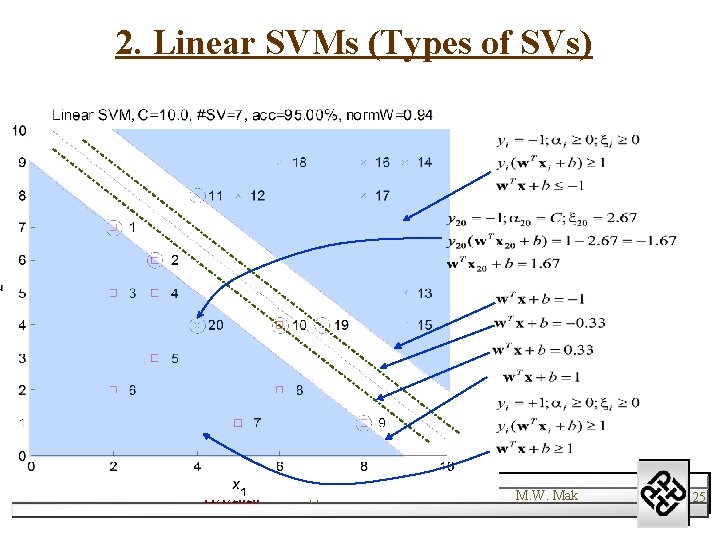
2. Linear SVMs (Types of SVs) l Three types of support vectors 1. On the margin: 2. Inside the margin: 3. Outside the margin: 11/1/2020 Support Vector Machines M. W. Mak 24

2. Linear SVMs (Types of SVs) 11/1/2020 Support Vector Machines M. W. Mak 25

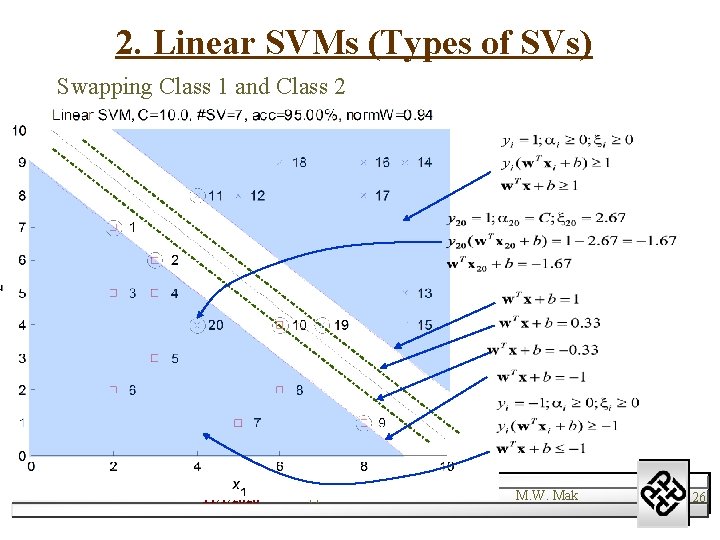
2. Linear SVMs (Types of SVs) Swapping Class 1 and Class 2 11/1/2020 Support Vector Machines M. W. Mak 26

2. Linear SVMs (Types of SVs) l Effect of varying C: C = 0. 1 C = 100 11/1/2020 Support Vector Machines M. W. Mak 27

3. Non-linear SVMs l In case the training data X are not linearly separable, we may use a kernel function to map the data from the input space to a feature space where data become linearly separable. Decision boundary Input Space (Domain X) 11/1/2020 Support Vector Machines Feature Space M. W. Mak 28

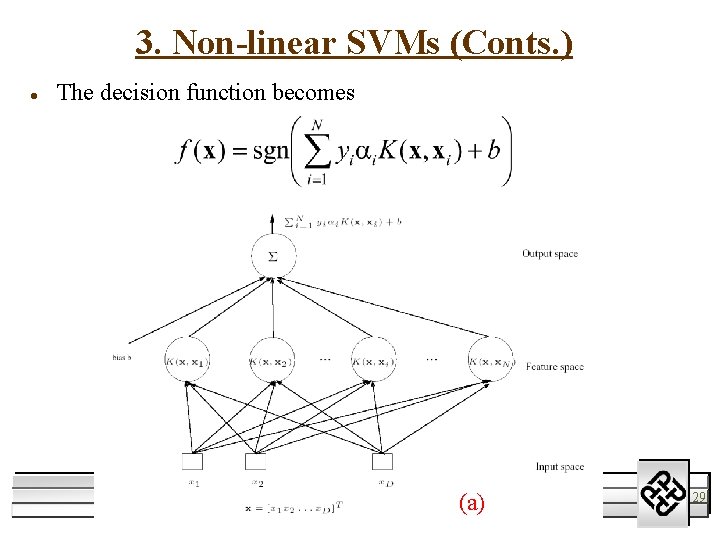
3. Non-linear SVMs (Conts. ) l The decision function becomes 11/1/2020 Support Vector Machines (a) M. W. Mak 29

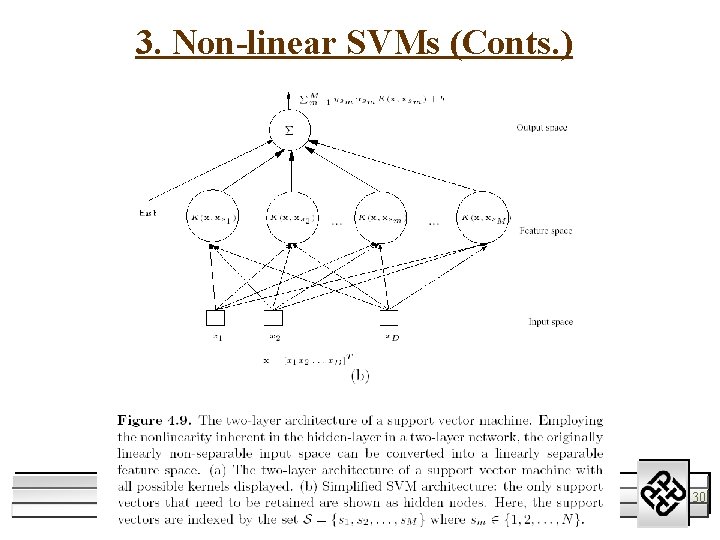
3. Non-linear SVMs (Conts. ) 11/1/2020 Support Vector Machines M. W. Mak 30

3. Non-linear SVMs (Conts. ) l The decision function becomes l For RBF kernels l For polynomial kernels 11/1/2020 Support Vector Machines M. W. Mak 31

3. Non-linear SVMs (Conts. ) l The optimization problem becomes: (9) l The decision function becomes 11/1/2020 Support Vector Machines M. W. Mak 32

3. Non-linear SVMs (Conts. ) l The effect of varying C on RBF-SVMs: C = 1000 C = 10 11/1/2020 Support Vector Machines M. W. Mak 33

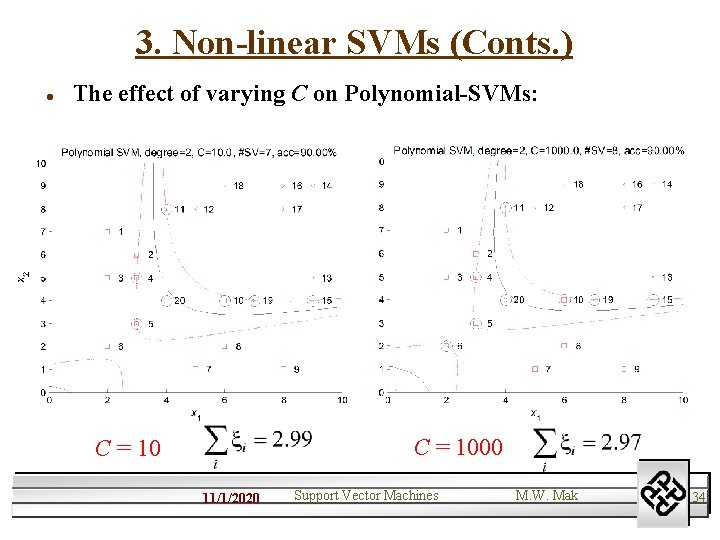
3. Non-linear SVMs (Conts. ) l The effect of varying C on Polynomial-SVMs: C = 1000 C = 10 11/1/2020 Support Vector Machines M. W. Mak 34