Support Vector Machine SVM Classification Greg Grudic Intro

Support Vector Machine (SVM) Classification Greg Grudic Intro AI 1

Today’s Lecture Goals • Support Vector Machine (SVM) Classification – Another algorithm for linear separating hyperplanes A Good text on SVMs: Bernhard Schölkopf and Alex Smola. Learning with Kernels. MIT Press, Cambridge, MA, 2002 Greg Grudic Intro AI 2

Support Vector Machine (SVM) Classification • Classification as a problem of finding optimal (canonical) linear hyperplanes. • Optimal Linear Separating Hyperplanes: – In Input Space – In Kernel Space • Can be non-linear Greg Grudic Intro AI 3

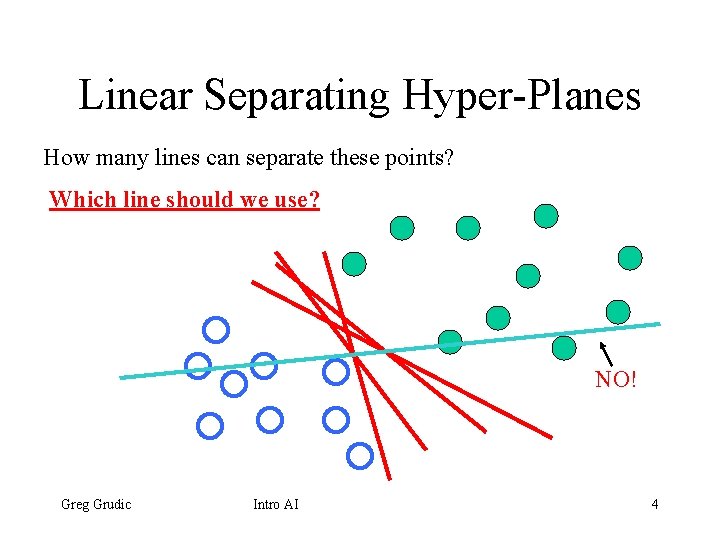
Linear Separating Hyper-Planes How many lines can separate these points? Which line should we use? NO! Greg Grudic Intro AI 4

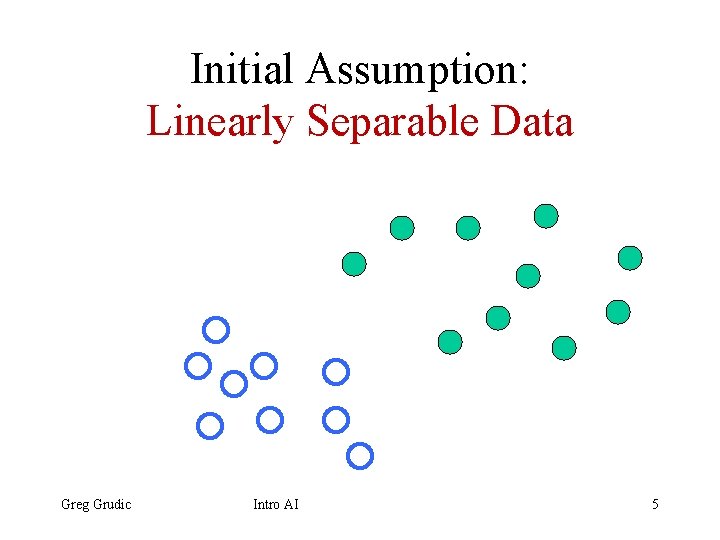
Initial Assumption: Linearly Separable Data Greg Grudic Intro AI 5

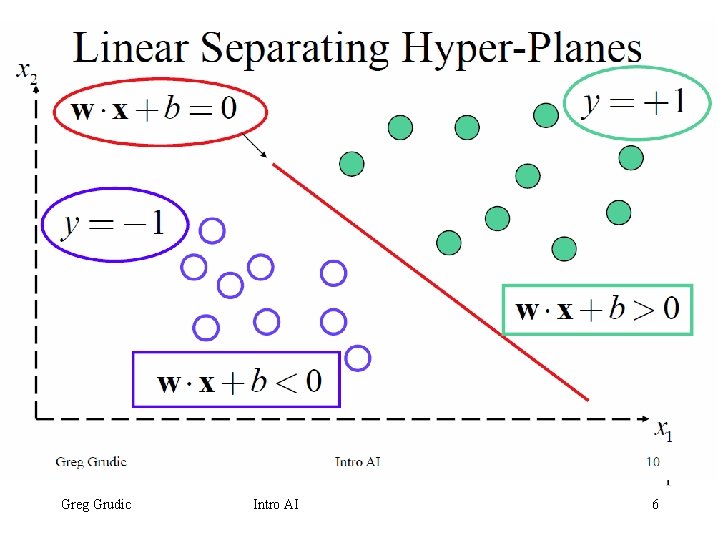
Linear Separating Hyper-Planes Greg Grudic Intro AI 6

Linear Separating Hyper-Planes • Given data: • Finding a separating hyperplane can be posed as a constraint satisfaction problem (CSP): • Or, equivalently: • If data is linearly separable, there an infinite number of hyperplanes that satisfy this CSP Greg Grudic Intro AI 7

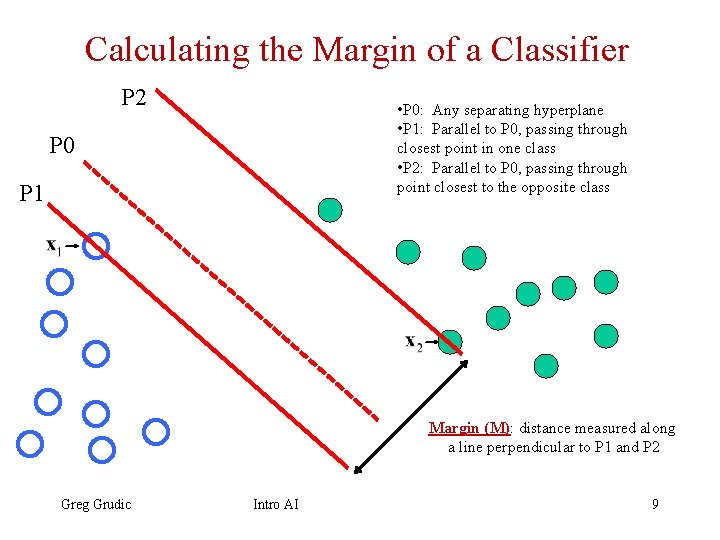
The Margin of a Classifier • Take any hyper-plane (P 0) that separates the data • Put a parallel hyper-plane (P 1) on a point in class 1 closest to P 0 • Put a second parallel hyper-plane (P 2) on a point in class -1 closest to P 0 • The margin (M) is the perpendicular distance between P 1 and P 2 Greg Grudic Intro AI 8

Calculating the Margin of a Classifier P 2 • P 0: Any separating hyperplane • P 1: Parallel to P 0, passing through closest point in one class • P 2: Parallel to P 0, passing through point closest to the opposite class P 0 P 1 Margin (M): distance measured along a line perpendicular to P 1 and P 2 Greg Grudic Intro AI 9

SVM Constraints on the Model Parameters Model parameters for on P 1 and for must be chosen such that, on P 2: For any P 0, these constraints are always attainable. Given the above, then the linear separating boundary lies half way between P 1 and P 2 and is given by: Resulting Classifier: Greg Grudic Intro AI 10

Remember: signed distance from a point to a hyperplane: Hyperplane define by: Greg Grudic Intro AI 11

Calculating the Margin (1) Greg Grudic Intro AI 12

Calculating the Margin (2) Signed Distance Take absolute value to get the unsigned margin: Greg Grudic Intro AI 13

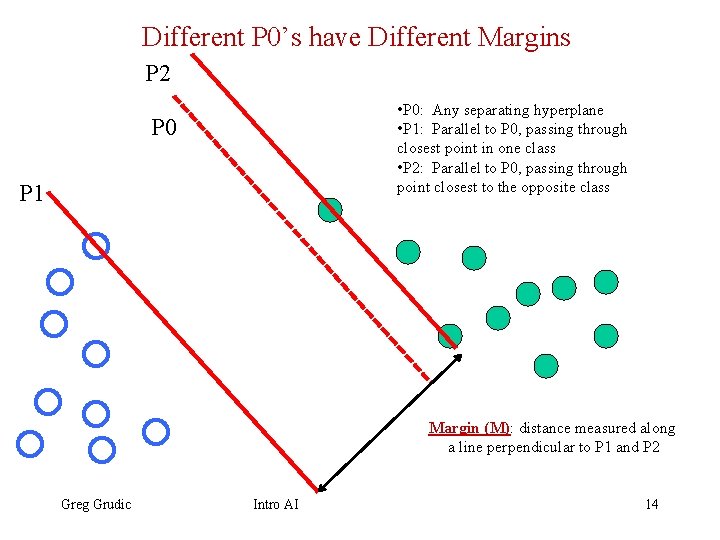
Different P 0’s have Different Margins P 2 • P 0: Any separating hyperplane • P 1: Parallel to P 0, passing through closest point in one class • P 2: Parallel to P 0, passing through point closest to the opposite class P 0 P 1 Margin (M): distance measured along a line perpendicular to P 1 and P 2 Greg Grudic Intro AI 14

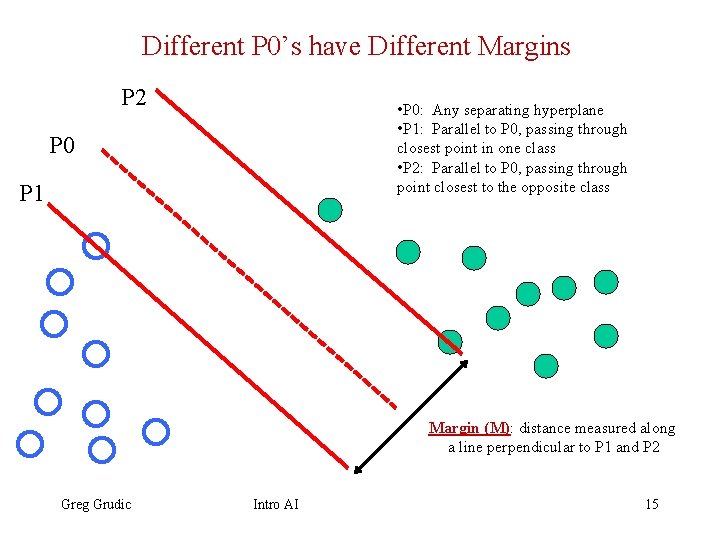
Different P 0’s have Different Margins P 2 • P 0: Any separating hyperplane • P 1: Parallel to P 0, passing through closest point in one class • P 2: Parallel to P 0, passing through point closest to the opposite class P 0 P 1 Margin (M): distance measured along a line perpendicular to P 1 and P 2 Greg Grudic Intro AI 15

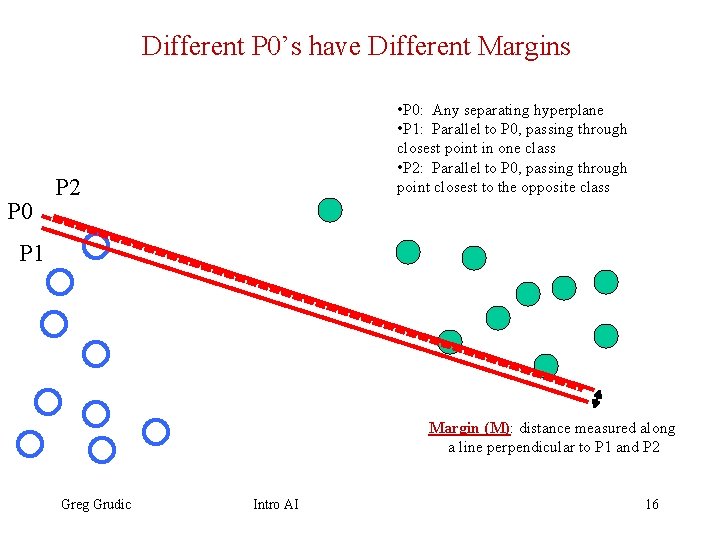
Different P 0’s have Different Margins P 0 • P 0: Any separating hyperplane • P 1: Parallel to P 0, passing through closest point in one class • P 2: Parallel to P 0, passing through point closest to the opposite class P 2 P 1 Margin (M): distance measured along a line perpendicular to P 1 and P 2 Greg Grudic Intro AI 16

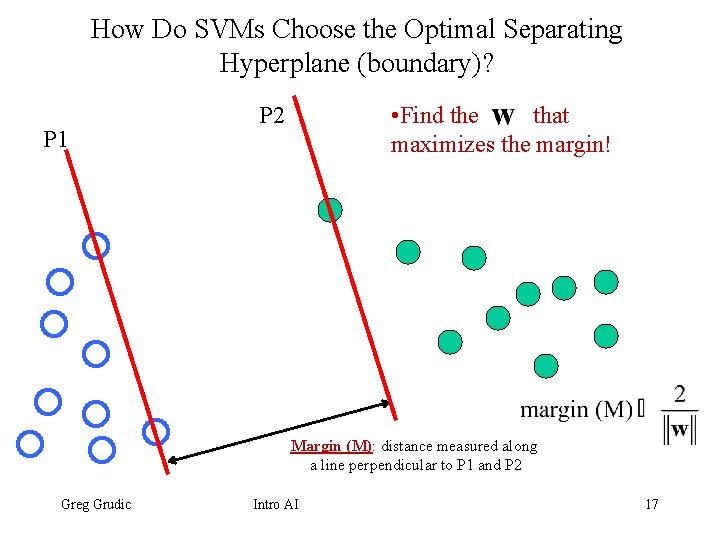
How Do SVMs Choose the Optimal Separating Hyperplane (boundary)? P 1 • Find the that maximizes the margin! P 2 Margin (M): distance measured along a line perpendicular to P 1 and P 2 Greg Grudic Intro AI 17

SVM: Constraint Optimization Problem • Given data: • Minimize subject to: The Lagrange Function Formulation is used to solve this Minimization Problem Greg Grudic Intro AI 18

The Lagrange Function Formulation For every constraint we introduce a Lagrange Multiplier: The Lagrangian is then defined by: Where - the primal variables are - the dual variables are Goal: Minimize Lagrangian w. r. t. primal variables, and Maximize w. r. t. dual variables Greg Grudic Intro AI 19

Derivation of the Dual Problem • At the saddle point (extremum w. r. t. primal) • This give the conditions • Substitute into Greg Grudic to get the dual problem Intro AI 20

Using the Lagrange Function Formulation, we get the Dual Problem • Maximize • Subject to Greg Grudic Intro AI 21

Properties of the Dual Problem • Solving the Dual gives a solution to the original constraint optimization problem • For SVMs, the Dual problem is a Quadratic Optimization Problem which has a globally optimal solution • Gives insights into the NON-Linear formulation for SVMs Greg Grudic Intro AI 22

Support Vector Expansion (1) OR is also computed from the optimal dual variables Greg Grudic Intro AI 23

Support Vector Expansion (2) Substitute OR Greg Grudic Intro AI 24

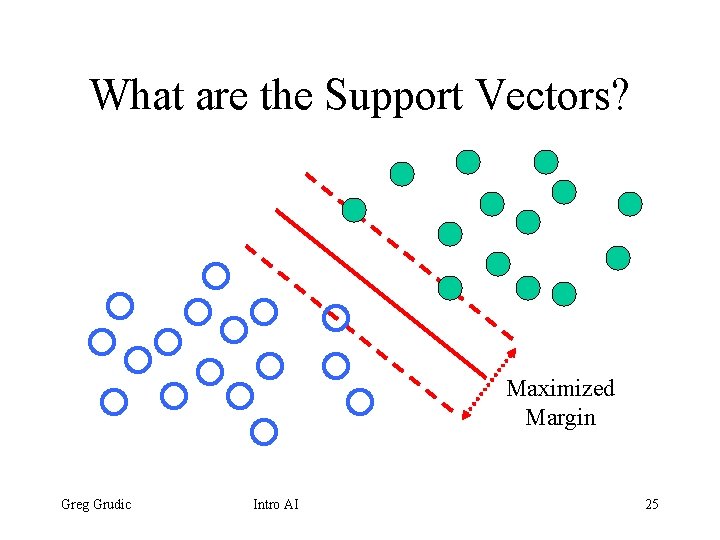
What are the Support Vectors? Maximized Margin Greg Grudic Intro AI 25

Why do we want a model with only a few SVs? • Leaving out an example that does not become an SV gives the same solution! • Theorem (Vapnik and Chervonenkis, 1974): Let be the number of SVs obtained by training on N examples randomly drawn from P(X, Y), and E be an expectation. Then Greg Grudic Intro AI 26

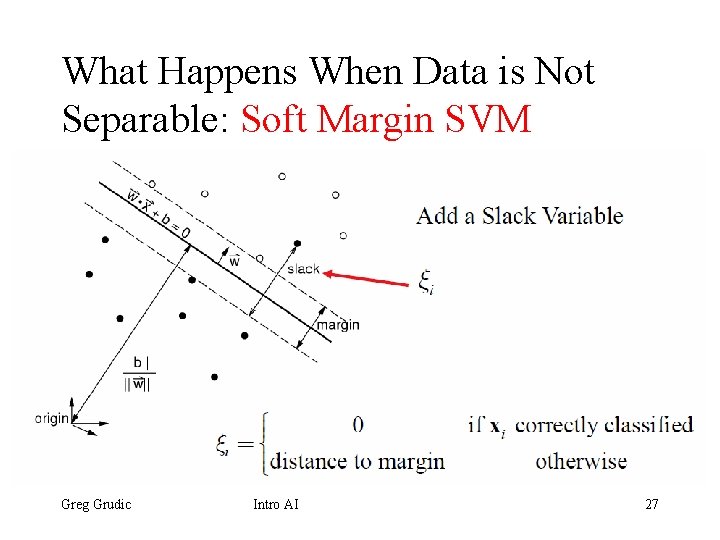
What Happens When Data is Not Separable: Soft Margin SVM Add a Slack Variable Greg Grudic Intro AI 27

Soft Margin SVM: Constraint Optimization Problem • Given data: • Minimize Greg Grudic subject to: Intro AI 28

Dual Problem (Non-separable data) • Maximize • Subject to Greg Grudic Intro AI 29

Same Decision Boundary Greg Grudic Intro AI 30

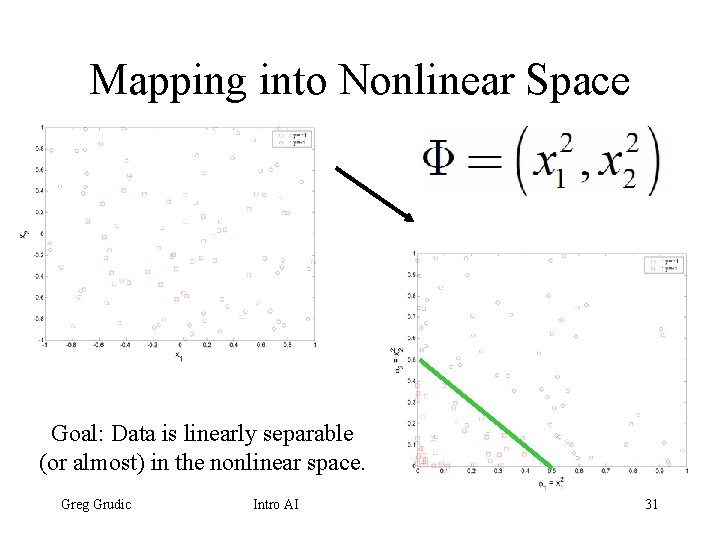
Mapping into Nonlinear Space Goal: Data is linearly separable (or almost) in the nonlinear space. Greg Grudic Intro AI 31

Nonlinear SVMs • KEY IDEA: Note that both the decision boundary and dual optimization formulation use dot products in input space only! Greg Grudic Intro AI 32

Kernel Trick Replace with Inner Product Can use the same algorithms in nonlinear kernel space! Greg Grudic Intro AI 33

Nonlinear SVMs Maximize: Boundary: Greg Grudic Intro AI 34

Need Mercer Kernels Greg Grudic Intro AI 35

Gram (Kernel) Matrix Training Data: Properties: • Positive Definite Matrix • Symmetric • Positive on diagonal • N by N Greg Grudic Intro AI 36

Commonly Used Mercer Kernels • Polynomial • Sigmoid • Gaussian Greg Grudic Intro AI 37

Why these kernels? • There are infinitely many kernels – The best kernel is data set dependent – We can only know which kernels are good by trying them and estimating error rates on future data • Definition: a universal approximator is a mapping that can arbitrarily well model any surface (i. e. many to one mapping) • Motivation for the most commonly used kernels – Polynomials (given enough terms) are universal approximators • However, Polynomial Kernels are not universal approximators because they cannot represent all polynomial interactions – Sigmoid functions (given enough training examples) are universal approximators – Gaussian Kernels (given enough training examples) are universal approximators – These kernels have shown to produce good models in practice Greg Grudic Intro AI 38

Picking a Model (A Kernel for SVMs)? • How do you pick the Kernels? – Kernel parameters • These are called learning parameters or hyperparamters – Two approaches choosing learning paramters • Bayesian – Learning parameters must maximize probability of correct classification on future data based on prior biases • Frequentist – Use the training data to learn the model parameters – Use validation data to pick the best hyperparameters. • More on learning parameter selection later Greg Grudic Intro AI 39

Greg Grudic Intro AI 40

Greg Grudic Intro AI 41

Greg Grudic Intro AI 42

Some SVM Software • LIBSVM – http: //www. csie. ntu. edu. tw/~cjlin/libsvm/ • SVM Light – http: //svmlight. joachims. org/ • Tiny. SVM – http: //chasen. org/~taku/software/Tiny. SVM/ • WEKA – http: //www. cs. waikato. ac. nz/ml/weka/ – Has many ML algorithm implementations in JAVA Greg Grudic Intro AI 43

MNIST: A SVM Success Story • Handwritten character benchmark – 60, 000 training and 10, 0000 testing – Dimension d = 28 x 28 Greg Grudic Intro AI 44

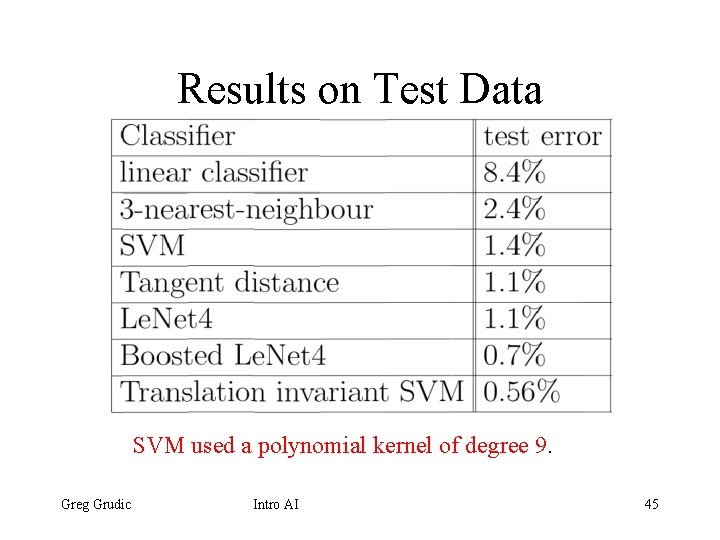
Results on Test Data SVM used a polynomial kernel of degree 9. Greg Grudic Intro AI 45

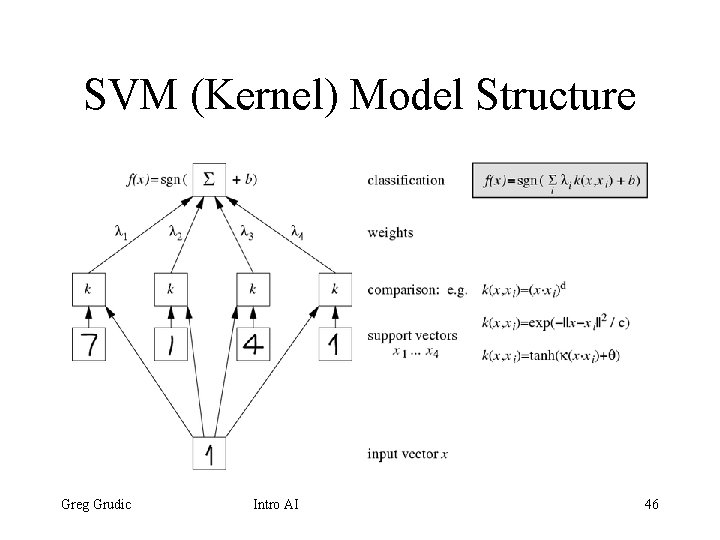
SVM (Kernel) Model Structure Greg Grudic Intro AI 46