Supervised Time Series Pattern Discovery through Local Importance

Supervised Time Series Pattern Discovery through Local Importance Mustafa Gokce Baydogan* George Runger* Eugene Tuv† * Arizona State University † Intel Corporation 10/14/2012 INFORMS Annual Meeting 2012, Phoenix

Outline p Time series classification n n Problem definition Motivation p Supervised Time Series Pattern Discovery through Local Importance (TS-PD) p Computational experiments and results p Conclusions and future work Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 2

Time Series Classification p Time series classification is a supervised learning problem n n n The input consists of a set of training examples and associated class labels, Each example is formed by one or more time series Predict the class of the new (test) series Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 3

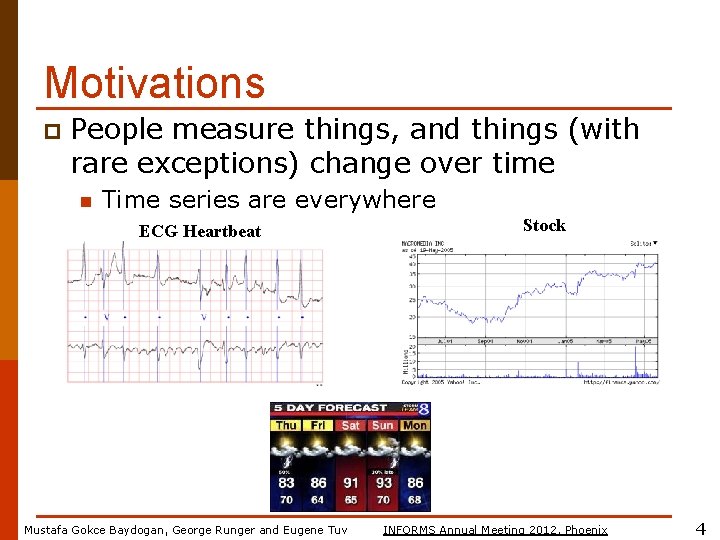
Motivations p People measure things, and things (with rare exceptions) change over time n Time series are everywhere ECG Heartbeat Mustafa Gokce Baydogan, George Runger and Eugene Tuv Stock INFORMS Annual Meeting 2012, Phoenix 4

Motivations p Other types of data can be converted to time series. n p Everything is about the representation. Example: Recognizing words An example word “Alexandria” from the dataset of word profiles for George Washington's manuscripts. A word can be represented by two time series created by moving over and under the word Images from E. Keogh. A quick tour of the datasets for VLDB 2008. In VLDB, 2008. Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 5

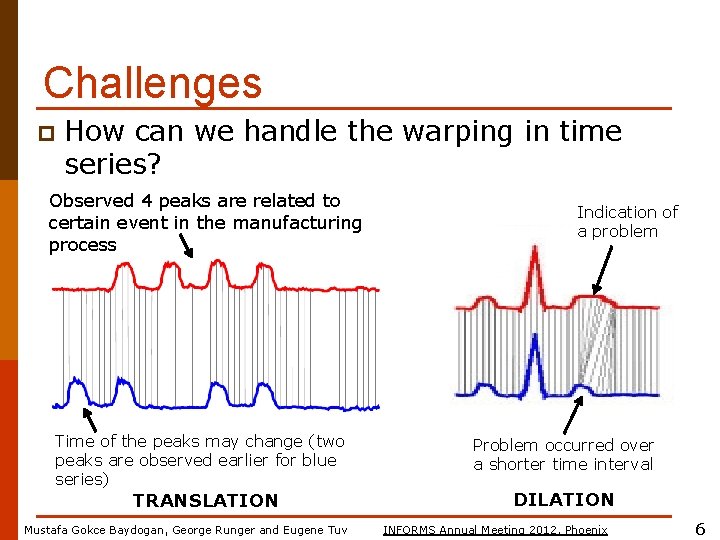
Challenges p How can we handle the warping in time series? Observed 4 peaks are related to certain event in the manufacturing process Time of the peaks may change (two peaks are observed earlier for blue series) TRANSLATION Mustafa Gokce Baydogan, George Runger and Eugene Tuv Indication of a problem Problem occurred over a shorter time interval DILATION INFORMS Annual Meeting 2012, Phoenix 6

Approaches p Instance-based methods p Predict based on the similarity to the training time series § § p Requires a similarity measure (distance measure) § Euclidean distance § …. Dynamic Time Warping (DTW) distance is known to be strong solution [1] § Handles translations and dilations by matching observations Feature-based methods p p Predict a test instance based on a model trained on extracted feature vectors Requires feature extraction methods and a supervised learner (i. e. decision tree, support vector machine, etc. ) to be trained on the extracted features Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 7

Instance-based methods p Advantages n n p Accurate Not requiring setting of many parameters Disadvantages n May not be suitable for real time applications [3] p n Not scalable with large number of training samples and variables, p p n DTW has a time complexity of O(n) using a lower bound (LB_Keogh [8]) (it is a variation of shortest path problem) § n is the length of the time series No model, each test series is compared to all (or some) training series Requires storage of the training time series § Not suitable for resource limited environments (i. e. sensors) Performance degrades with long time series and short features of interest Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 8

Feature-based methods p Time series are represented by the features generated. n Shape-based features p n Wavelet features p n Mean, variance, slope … … Coefficients … p Global features provide a compact representation of the series (such as global mean/variance) p Local features are important p Features from time series segments (intervals) mean Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 9

Feature-based methods p Advantages n n n Fast Robust to noise Fusion of domain knowledge p Features specific to domain § i. e. Linear predictive coding (LPC) features for speech recognition p Disadvantages n n Problems in handling warping Cardinality of the feature set may vary Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 10

Time Series Pattern Discovery through Local Importance (TS-PD) p Identifying the region of time series important to classification is required for n n p Interpretability Good classification with appropriate approaches (matching the patterns) Local importance is a measure that evaluates the potential descriptiveness of certain segment (interval) of the time series Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 11

TS-PD Local Importance p Time series are represented by the interval features Mean Variance Slope p A tree-based ensemble is trained on this representation (Random Forest) -> RFint n Any features can be added to representation p p p Different scales Currently shape-based Application specific? A permutation-based approach to evaluate the descriptiveness of each interval (based on the out-of-bagging idea) Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 12

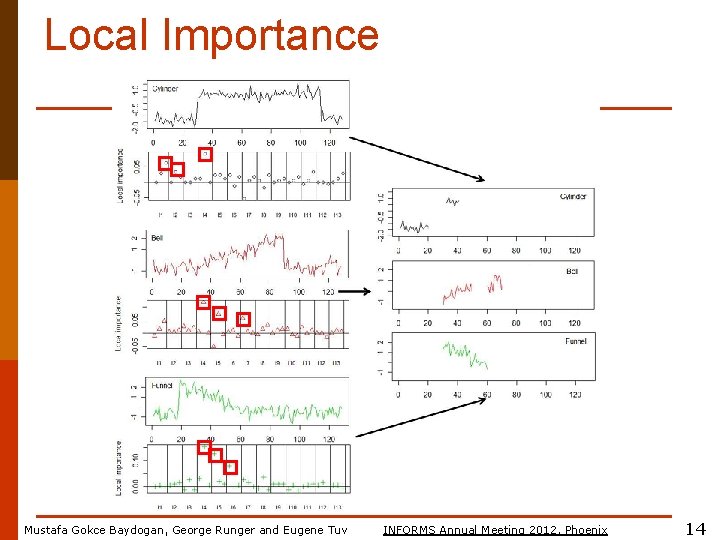
TS-PD Local Importance Train Test on permuted OOB samples Let time series 1 be of class 1 Local importance is defined = Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 13

Local Importance Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 14

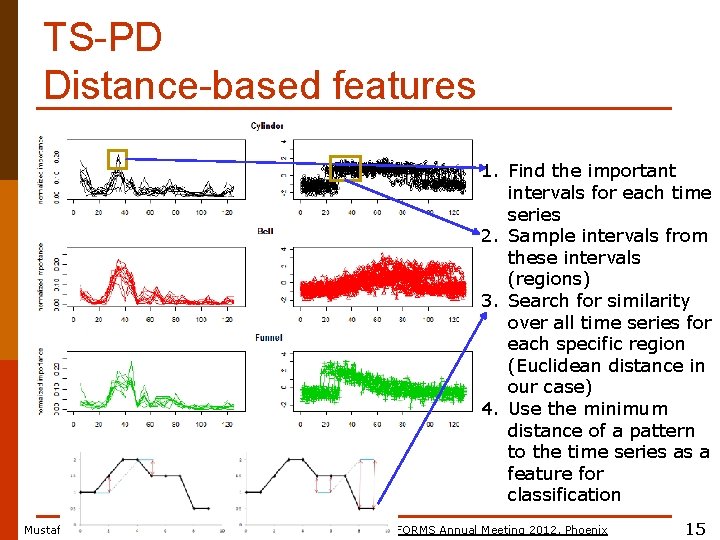
TS-PD Distance-based features 1. Find the important intervals for each time series 2. Sample intervals from these intervals (regions) 3. Search for similarity over all time series for each specific region (Euclidean distance in our case) 4. Use the minimum distance of a pattern to the time series as a feature for classification Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 15

TS-PD Classification p In the feature set n n p Each row is a time series Each column is a pattern The entries are the distance of the region of the time series that is the most similar to the pattern Basically, a kernel based on the distances to the patterns A tree-based ensemble is trained on this feature set (Random Forest) -> RFts n n Scalable Variable importance measure Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 16

TS-PD Interpretability p Variable importance [9] enables interpretability n n Find the most important features from RF Visualize Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 17

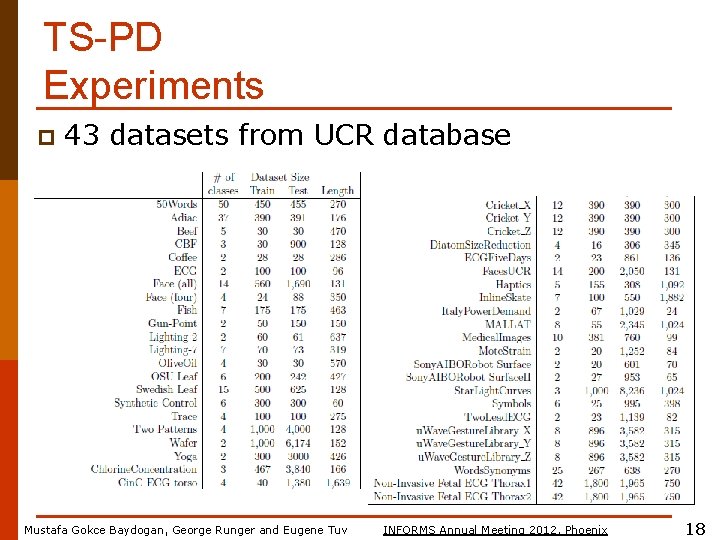
TS-PD Experiments p 43 datasets from UCR database Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 18

TS-PD Experiments p Parameters n Interval length and sliding window p Set small enough that probability of missing a pattern is decreased. 6 and 3 time units 10 n Number of locally important intervals to be used as intervals reference pattern p Depends on the dataset characteristics § If features of interest is long, larger setting preferred § Interval length also affects p RF is not affected by this setting if set large enough because of the embedded feature selection § Irrelevant patterns are easily identified § Correlated patterns are handled by building tree on random feature subspaces 2000 n Number of trees for both RF, RFint and RFts trees p p This can be easily set based on the OOB error rates If there is no concern about the computation time, larger setting is preferred Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 19

TS-PD Experiments p Two types of NN classifiers with DTW n n NNDTWNo. Win NNBest. DTW p searches for the best warping window, based on the training data Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 20

TS-PD Example p Extending TS-PD to MTS classification p Gesture recognition task [12] n n Acceleration of hand on x, y and z axis Classify gestures (8 different types of gestures) Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 21

TS-PD Example Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 22

TS-PD Conclusion p TS-PD identifies regions of interests n Provides a visualization tool for understanding underlying relations p Fast approach to detect the local information related to the classification p Handles the warping partially n n Handles translations Dilations? p Distance based features do not guarantee p Provides a kernel based on local distances p Interpretable and provides fast classification results For reproducibility of the results, the code of TS-PD is available on http: //www. mustafabaydogan. com/supervised-time-series-pattern-discovery-throughlocal-importance-tspd. html Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 23

Thanks! Questions and Comments? Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 24

References Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 25

References (continued) Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 26

References (continued) Mustafa Gokce Baydogan, George Runger and Eugene Tuv INFORMS Annual Meeting 2012, Phoenix 27