Supervised Learning Linear Perceptron NN Distinction Between Approximation

Supervised Learning: Linear Perceptron NN

Distinction Between Approximation. Based vs. Decision-Based NNs • Teacher in Approximation-Based NN are quantitative in real or complex values • Teacher in Decision-Based NNs are symbols, instead of numeric complex values.

Decision-Based NN (DBNN) • Linear Perceptron • Discriminant function (Score function) • Reinforced and Anti-reinforced Learning Rules • Hierarchical and Modular Structures

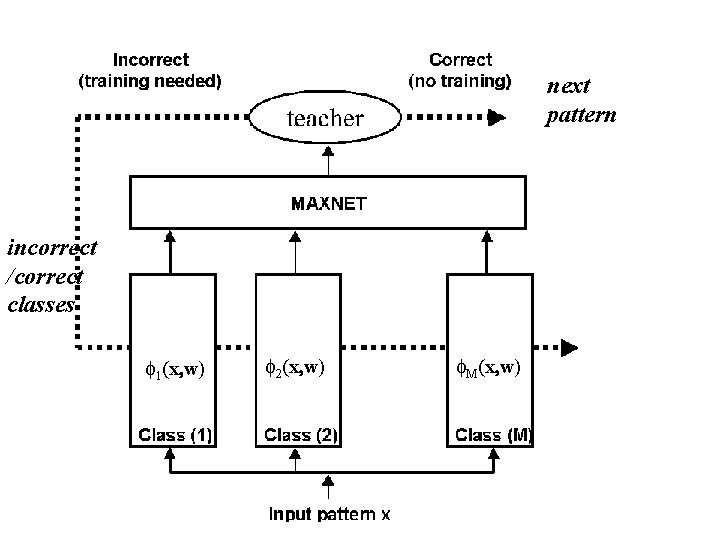
next pattern incorrect /correct classes f 1(x, w) f 2(x, w) f. M(x, w)

Supervised Learning: Linear Perceptron NN

Two-Classes: Linear Perceptron Learning Rule fj(x, wj ) = ▽fj T (x wj+w 0) = z. Tŵj (= z. Tw) ( z, wj ) = z Upon the presentation of the m-th training pattern z(m) , the weight vector w(m) is updated as w(m+1) = w(m) + h (t (m) - d (m) ) z(m) where h is a positive learning rate.

Linear Perceptron: Convergence Theorem (Two Classes) If a set of training patterns is linearly separable, then the linear perceptron learning algorithm converges to a correct solution in a finite number of iterations.

w(m+1) = w(m) + h (t (m) - d (m) ) z(m) It converges when learning rate h is small enough.

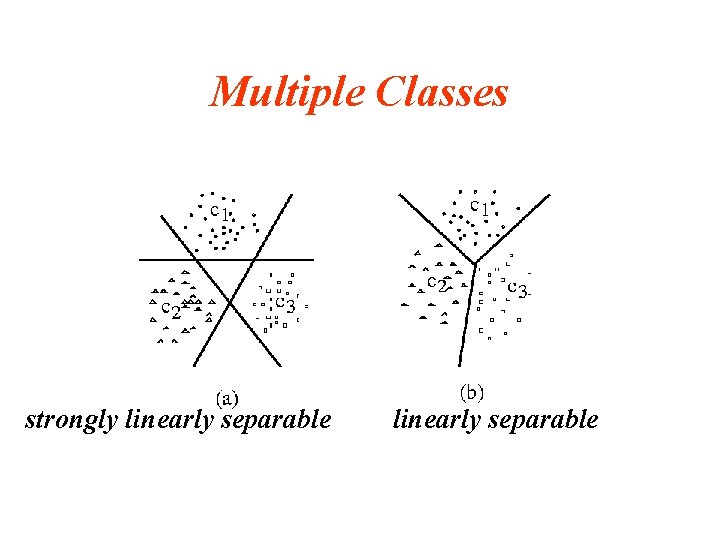
Multiple Classes strongly linearly separable

Linear Perceptron Convergence Theorem (Multiple Classes) If the given multiple-class training set is linearly separable, then the linear perceptron learning algorithm converges to a correct solution after a finite number of iterations.

Multiple Classes: Linear Perceptron Learning Rule (linearly separability)

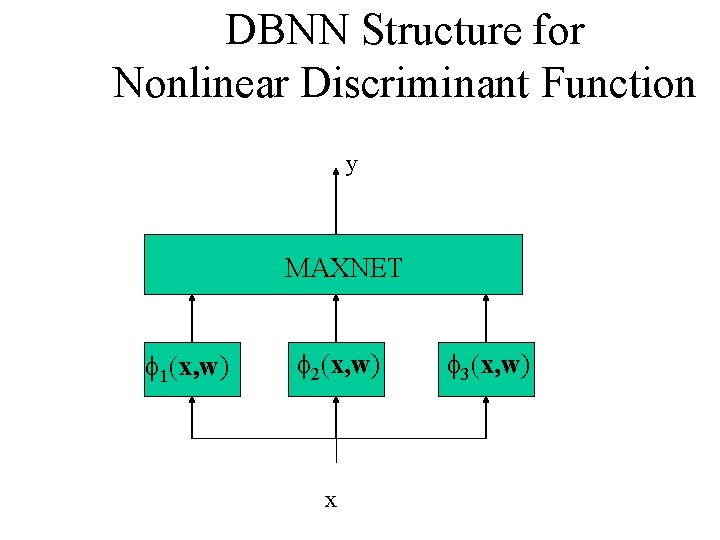
DBNN Structure for Nonlinear Discriminant Function y MAXNET f 1(x, w) f 2(x, w) x f 3(x, w)

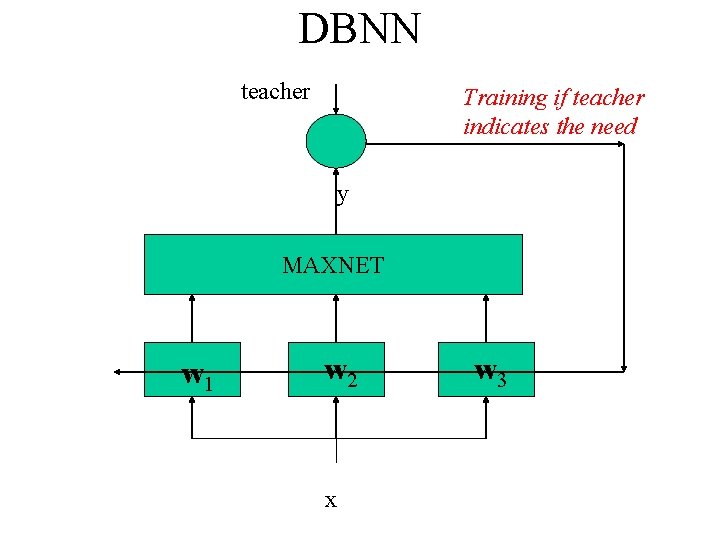
DBNN teacher Training if teacher indicates the need y MAXNET w 1 w 2 x w 3

Decision-based learning rule is based on a minimal updating principle. The rule tends to avoid or minimize unnecessary sideeffects due to overtraining. • One scenario is that the pattern is already correctly classified by the current network, then there will be no updating attributed to that pattern, and the learning process will proceed with the next training pattern. • The second scenario is that the pattern is incorrectly classified to another winning class. In this case, parameters of two classes must be updated. The score of the winning class should be reduced, by the anti-reinforced learning rule, while the score of the correct (but not winning) class should be enhanced by the reinforced learning rule.

Reinforced and Anti-reinforced Learning Suppose that the m -th training patternn x(m) , x(m) is known to belong to the i-th class. The leading challenger is denoted by j = arg maxi≠j φ( x(m), Θj ) Reinforced Learning D wi = + h wi fi ( x, w) Anti-Reinforced Learning D wj = - h wj fj ( x, w)

For Simple RBF Discriminant Function fj(x, wj ) =. 5(x - wj)2 ▽fj(x, wj ) = (x - wj) Upon the presentation of the m-th training pattern z(m) , the weight vector w(m) is updated as Reinforced Learning Anti-Reinforced Learning D wi = + h( x - wi) D wj = - h( x - wj)

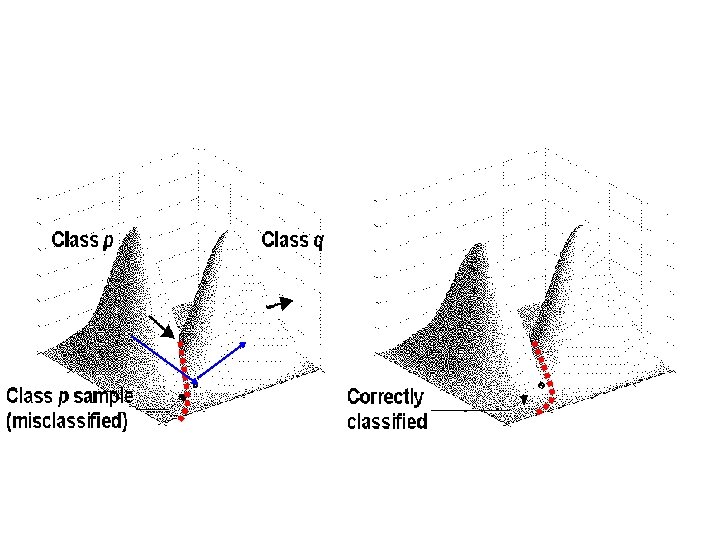
Decision-Based Learning Rule The learning scheme of the DBNN consis of two phases: • locally unsupervised learning. • globally supervised learning.

Locally Unsupervised Learning Via VQ or EM Clustering Method Several approaches can be used to estimate the number of hidden nodes or the initial clustering can be determined based on VQ or EM clustering methods. • EM allows the final decision to incorporate prior information. This could be instrumental to multipleexpert or multiple-channel information fusion.

Globally Supervised Learning Rules • The objective of learning is minimum classification error (not maximum likelihood estimation). • Inter-class mutual information is used to fine tune the decision boundaries (i. e. , the globally supervised learning). • In this phase, DBNN applies reinforced-antireinforced learning rule [Kung 95] , or discriminative learning rule [Juang 92] , to adjust network parameters. Only misclassified patterns need to be involved in this training phase.

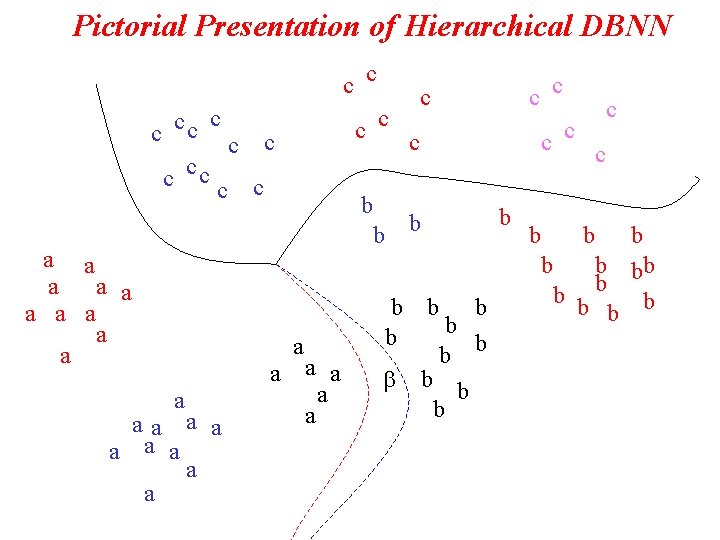
Pictorial Presentation of Hierarchical DBNN c cc c c b a a a aa a a a b b a a b c c c b b b c b b bb b b

Discriminant function (Score function) • LBF Function (or Mixture of) • RBF Function (or Mixture of) • Prediction Error Function • Likelihood Function : HMM

Hierarchical and Modular DBNN • Subcluster DBNN • Probabilistic DBNN • Local Experts via K-mean or EM • Reinforced and Anti-reinforced Learning

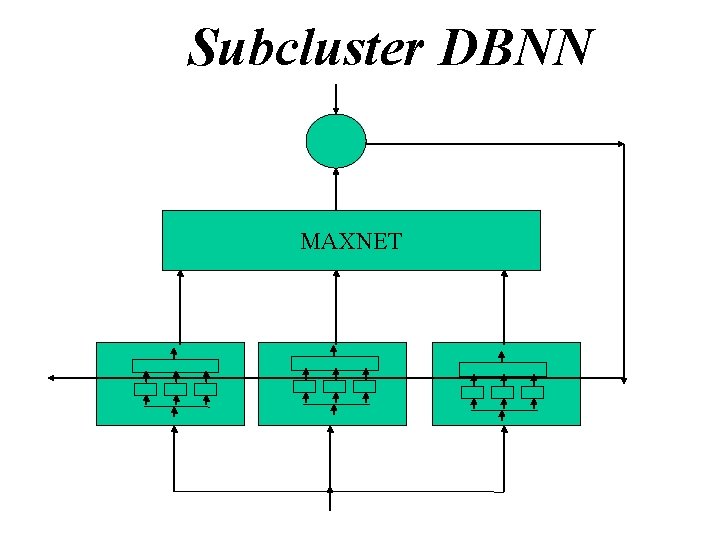
Subcluster DBNN MAXNET

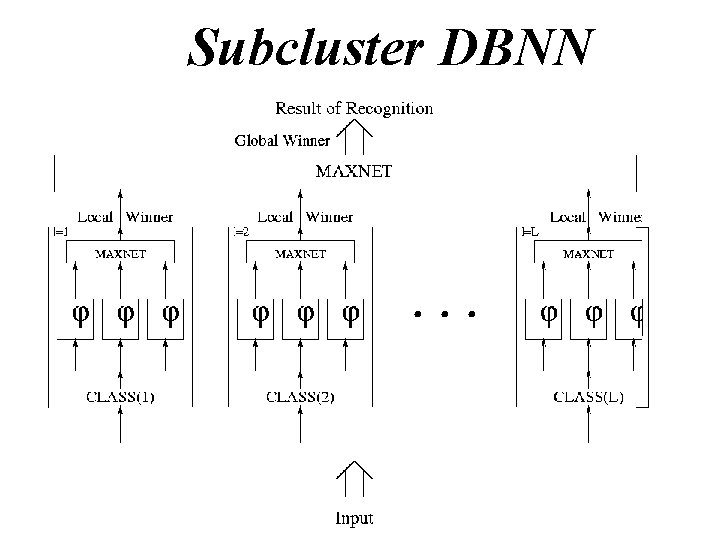
Subcluster DBNN

Subcluster Decision-Based Learning Rule

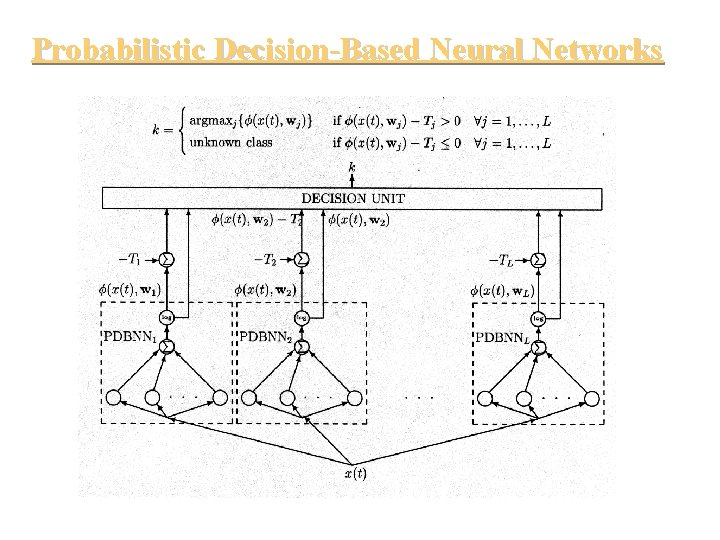
Probabilistic DBNN

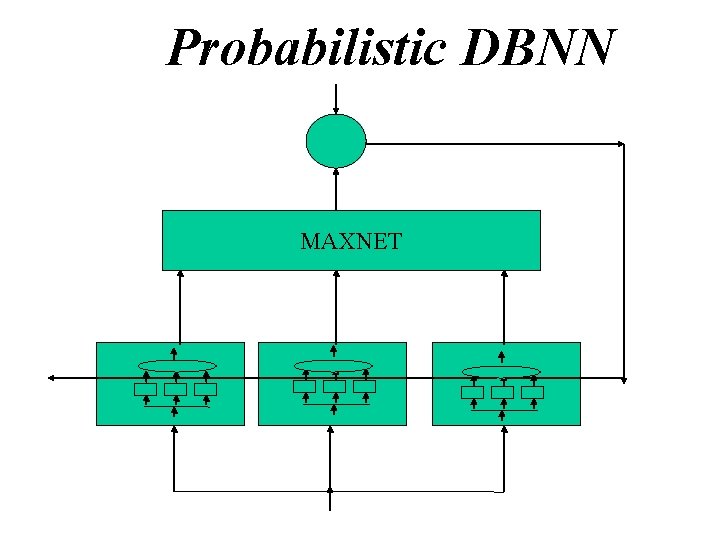
Probabilistic DBNN MAXNET

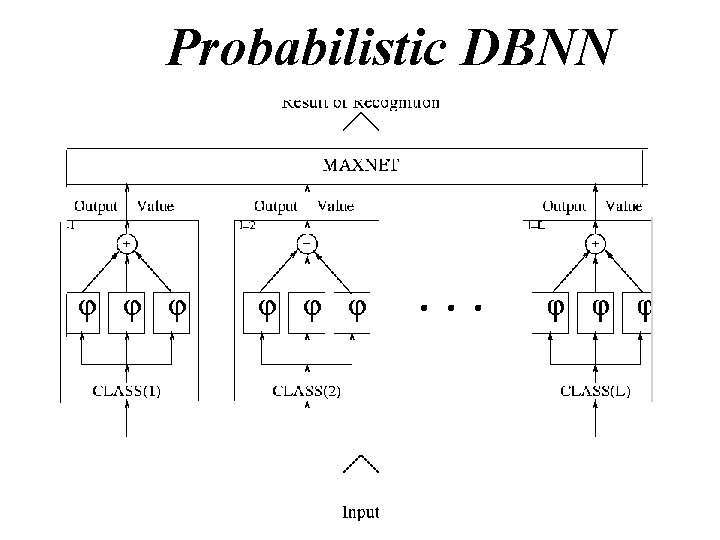
Probabilistic DBNN

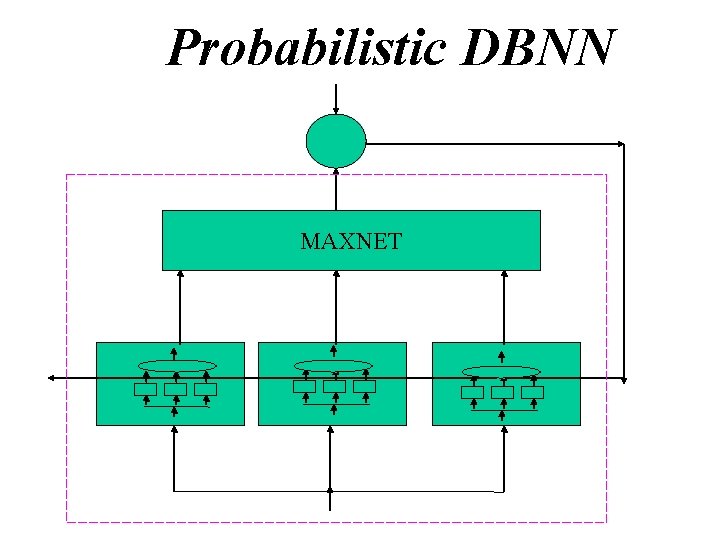
Probabilistic DBNN MAXNET

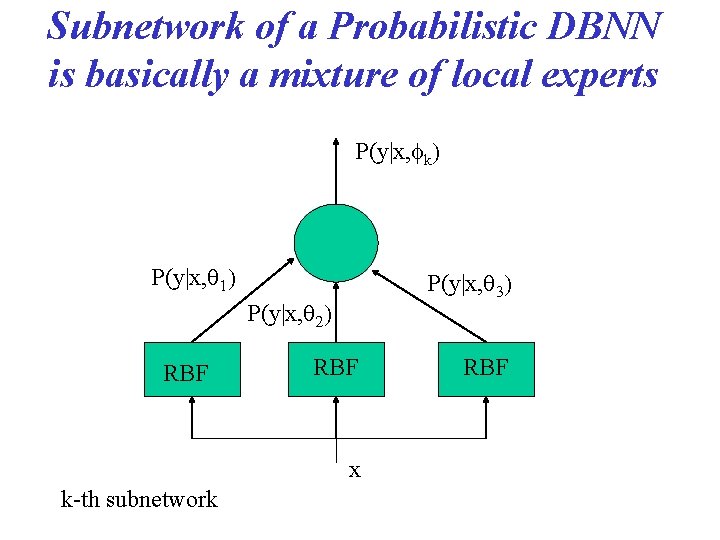
Subnetwork of a Probabilistic DBNN is basically a mixture of local experts P(y|x, fk) P(y|x, q 1) P(y|x, q 3) P(y|x, q 2) RBF x k-th subnetwork RBF

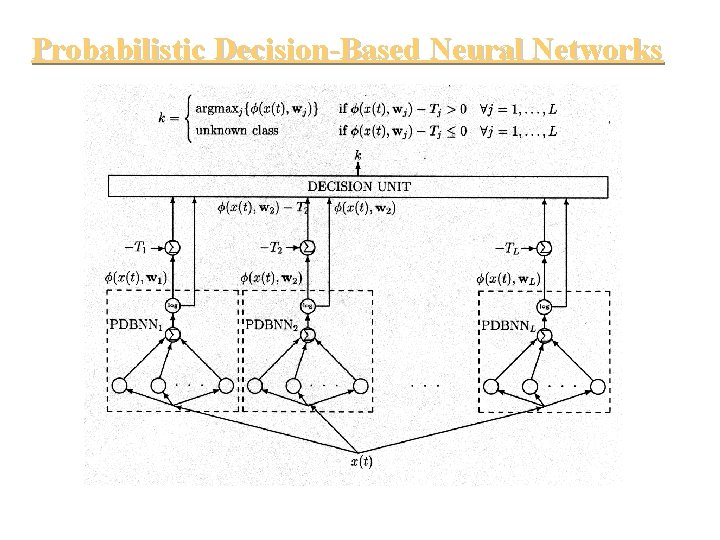
Probabilistic Decision-Based Neural Networks

Training of Probabilistic DBNN • Selection of initial local experts: Intra-class training Unsupervised training EM (Probabilistic) Training • Training of the experts: Inter-class training Supervised training Reinforced and Anti-reinforced Learning

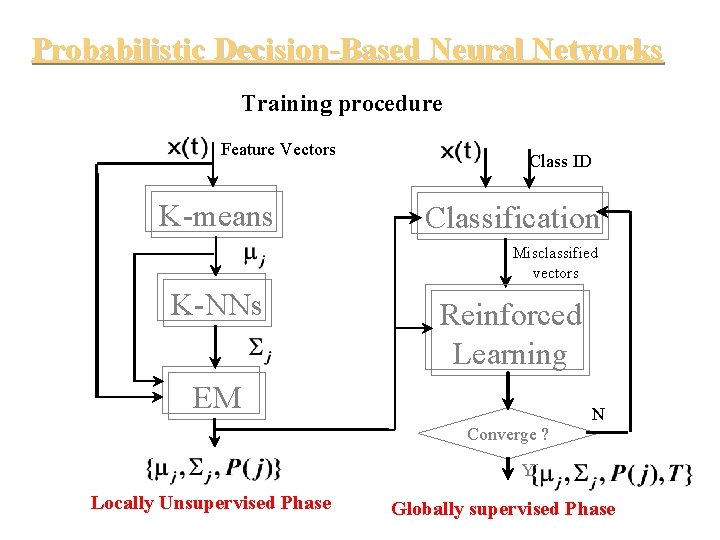
Probabilistic Decision-Based Neural Networks Training procedure Feature Vectors K-means Class ID Classification Misclassified vectors K-NNs Reinforced Learning EM N Converge ? Y Locally Unsupervised Phase Globally supervised Phase

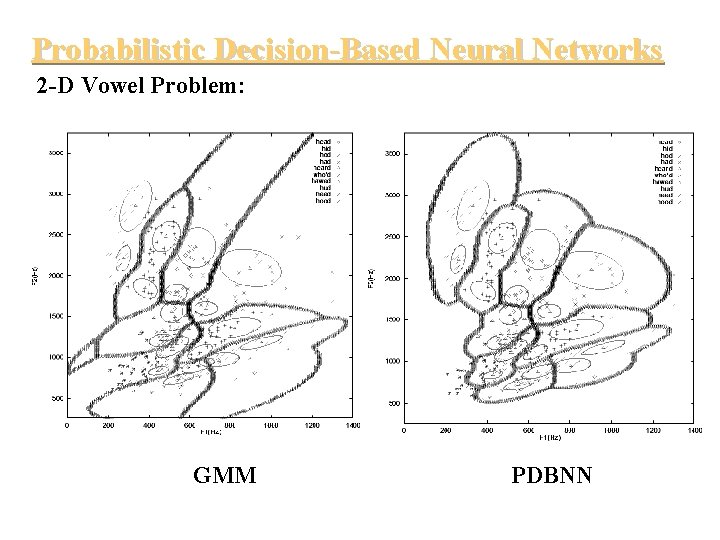
Probabilistic Decision-Based Neural Networks 2 -D Vowel Problem: GMM PDBNN

Difference of MOE and DBNN For MOE, the influence from the training patterns on each expert is regulated by the gating network (which itself is under training) so that as the training goes, the training patterns will have higher influence on the closer-by experts, and lower influence on the far-away ones. (The MOE updates all the classes. ) Unlike the MOE, the DBNN makes use of both unsupervised (EM-type) and supervised (decision-based) learning rules. The DBNN uses only mis-classified training patterns for its globally supervised learning. The DBNN updates only the ``winner" class and the class which the mis-classified pattern actually belongs to. Its training strategy is to abide by a ``minimal updating principle“.

DBNN/PDBNN Applications • • OCR (DBNN) Texture Segmentation(DBNN) Mammogram Diagnosis (PDBNN) Face Detection(PDBNN) Face Recognition (PDBNN) Money Recognition(PDBNN) Multimedia Library(DBNN)

OCR Classification (DBNN)

Image Texture Classification (DBNN)

Face Detection (PDBNN)

Face Recognition (PDBNN)

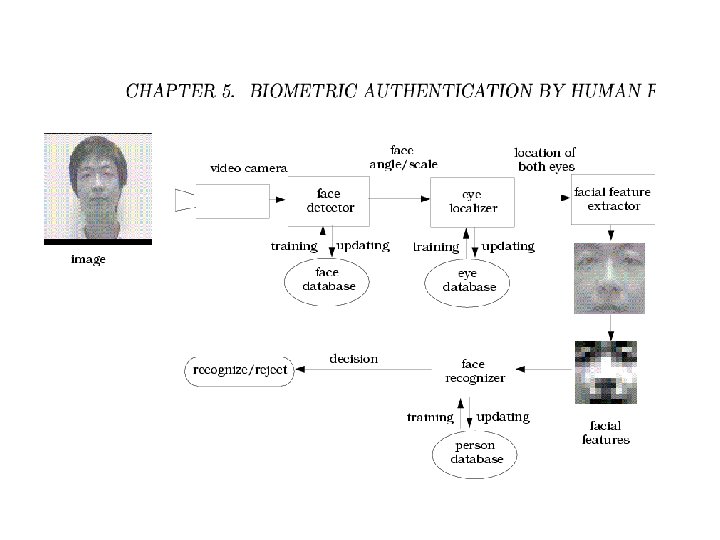
show movies

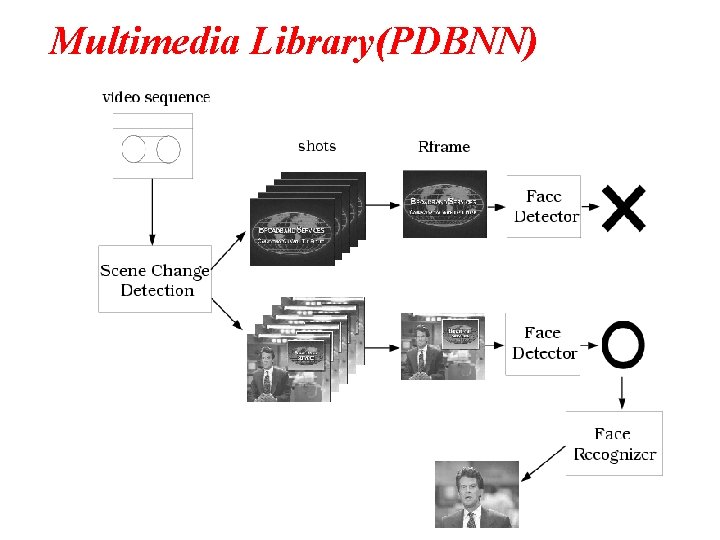
Multimedia Library(PDBNN)

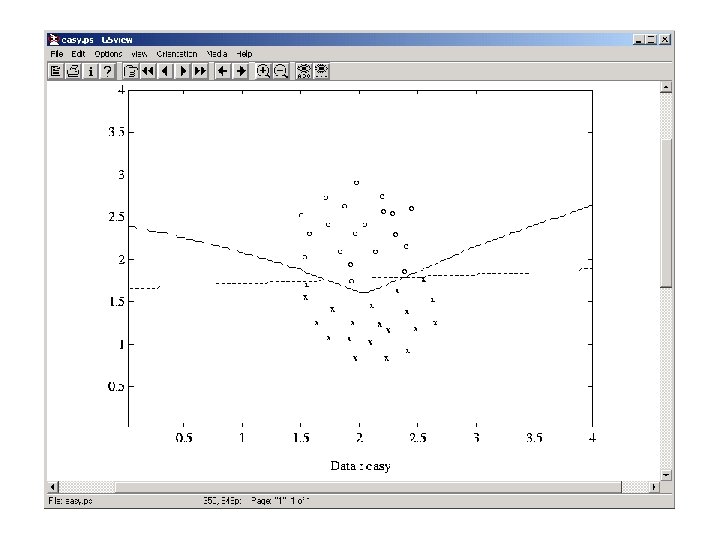
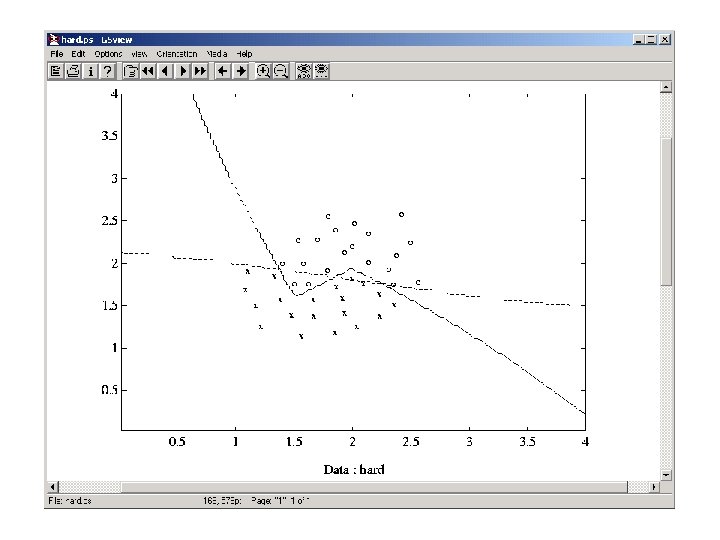
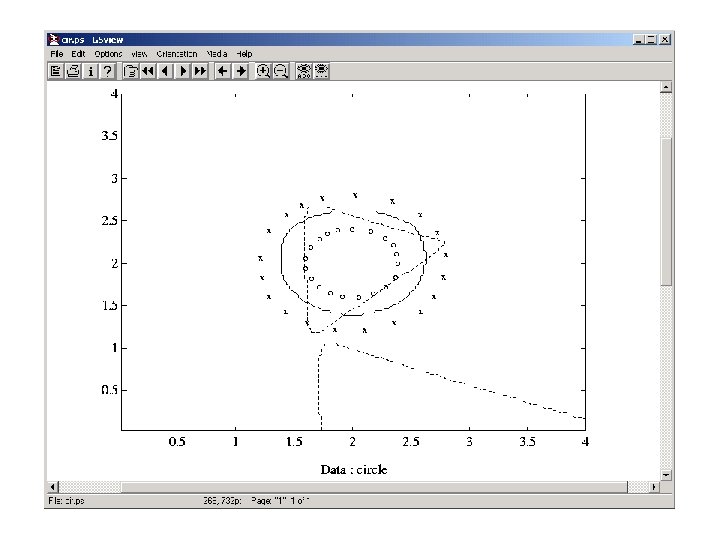
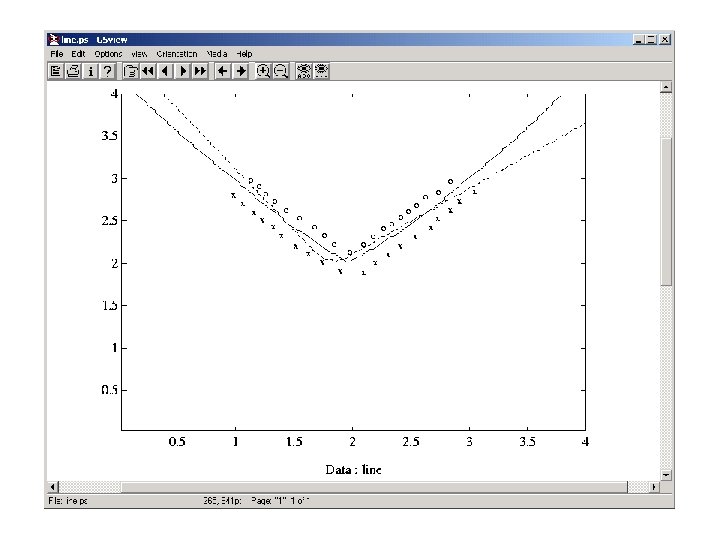
Mat. Lab Assignment #4: DBNN to separate 2 classes ratio=2: 1 • RBF DBNN with 4 centroids per class • RBF DBNN with 4 centroids and 6 centroids for green and blue classes respectively.

RBF-BP NN for Dynamic Resource Allocation • use content to determine renegotiation time • use content/ST-traffic to estimate how much resource to request Neural network traffic predictor yields smaller prediction MSE and higher link utilization.

Intelligent Media Agent Modern information technology in the internet era should support interactive and intelligent processing that transforms and transfers information. Integration of signal processing and neural net techniques could be a versatile tool to a broad spectrum of multimedia applications.

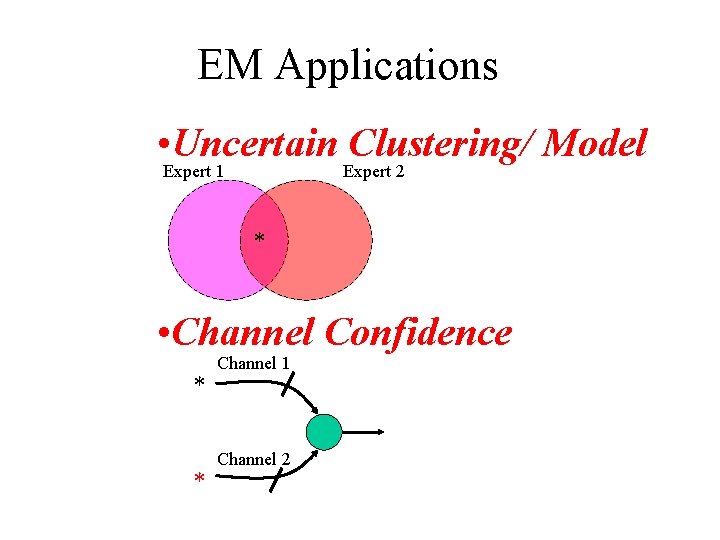
EM Applications • Uncertain Clustering/ Model Expert 1 Expert 2 * • Channel Confidence * * Channel 1 Channel 2

Channel Fusion

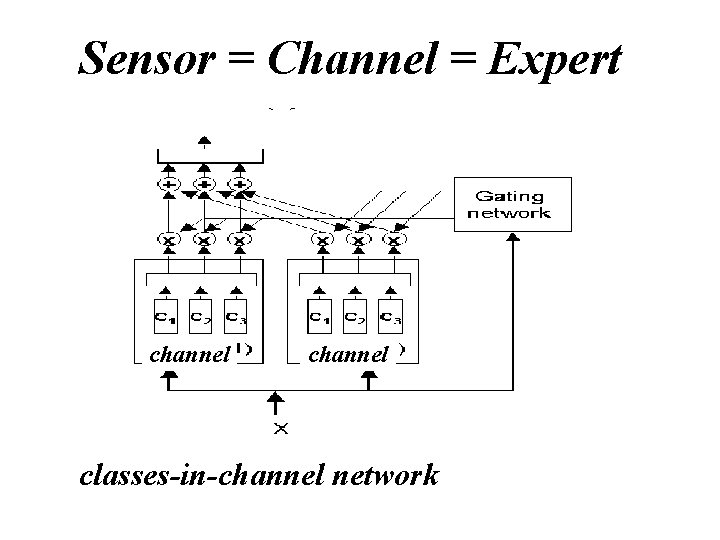
Sensor = Channel = Expert channel classes-in-channel network

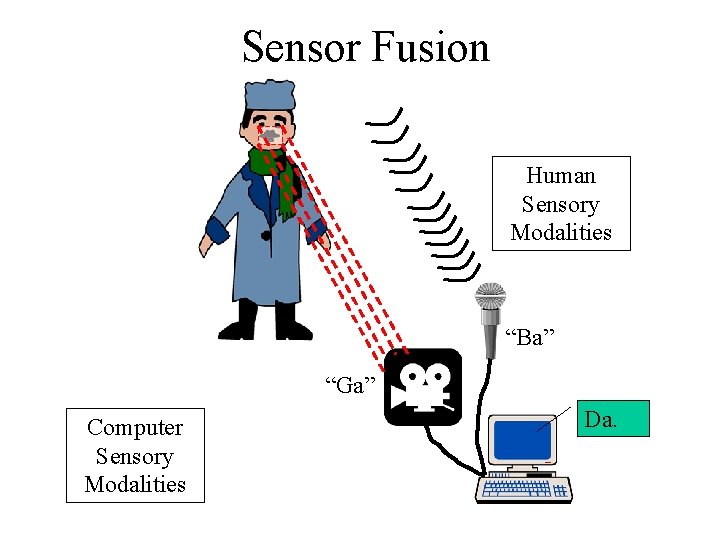
Sensor Fusion Human Sensory Modalities “Ba” “Ga” Computer Sensory Modalities Da.

Fusion Example Toy Car Recognition

Probabilistic Decision-Based Neural Networks

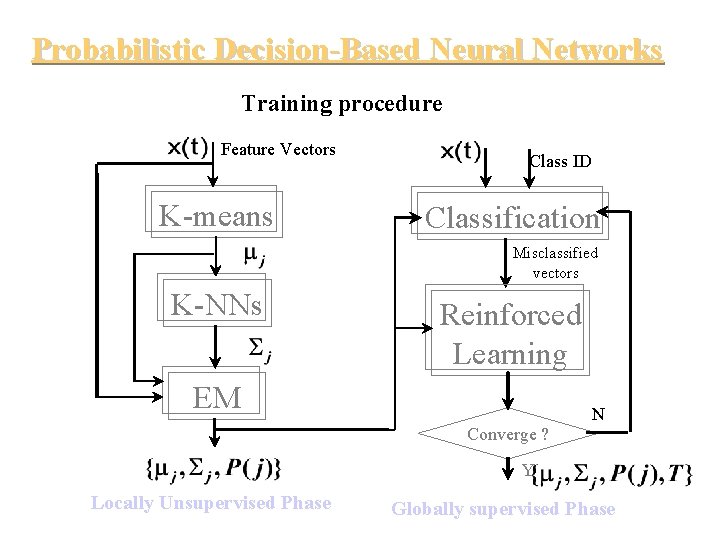
Probabilistic Decision-Based Neural Networks Training procedure Feature Vectors K-means Class ID Classification Misclassified vectors K-NNs Reinforced Learning EM N Converge ? Y Locally Unsupervised Phase Globally supervised Phase

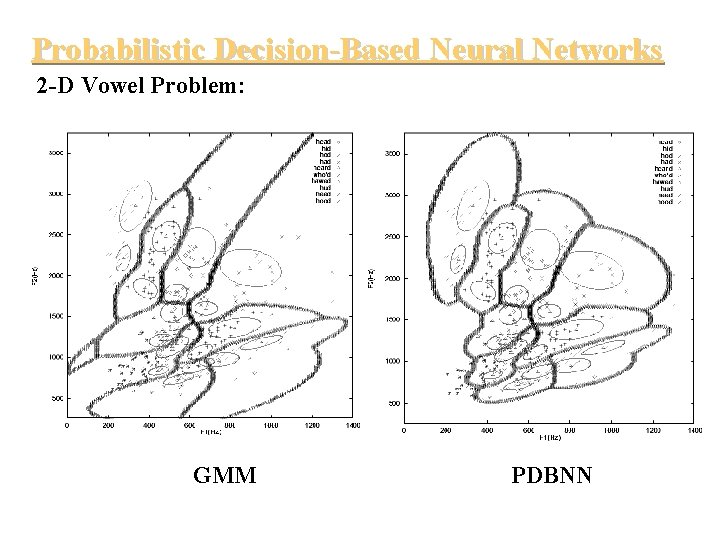
Probabilistic Decision-Based Neural Networks 2 -D Vowel Problem: GMM PDBNN

References: [1] Lin, S. H. , Kung, S. Y. and Lin, L. J. (1997). “Face recognition/detection by probabilistic decision-based neural network, IEEE Trans. on Neural Networks, 8 (1), pp. 114 -132. [2] Mak, M. W. et al. (1994), “Speaker Identification using Multi Layer Perceptrons and Radial Basis Functions Networks, ” Neurocomputing, 6 (1), 99 -118.