Superconductivity Introduction Thermal properties specific heat entropy free

Superconductivity • Introduction • Thermal properties • specific heat, entropy, free energy • Magnetic properties • critical field, critical current, Meissner effect, type II SC • London theory of the Meissner effect • penetration length, coherence length, surface energy • Microscopic (BCS) theory • Cooper pair, BCS ground state • Flux quantization Dept of Phys • Quantum tunneling • single particle tunneling, DC/AC Josephson effect • SQUID M. C. Chang

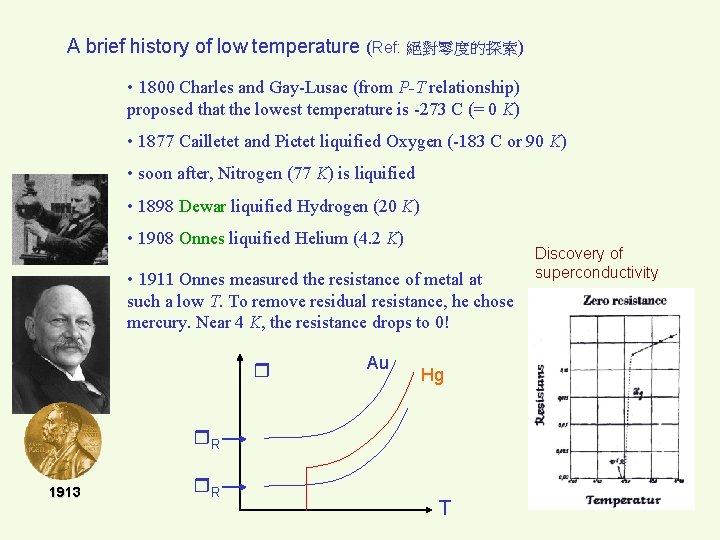
A brief history of low temperature (Ref: 絕對零度的探索) • 1800 Charles and Gay-Lusac (from P-T relationship) proposed that the lowest temperature is -273 C (= 0 K) • 1877 Cailletet and Pictet liquified Oxygen (-183 C or 90 K) • soon after, Nitrogen (77 K) is liquified • 1898 Dewar liquified Hydrogen (20 K) • 1908 Onnes liquified Helium (4. 2 K) • 1911 Onnes measured the resistance of metal at such a low T. To remove residual resistance, he chose mercury. Near 4 K, the resistance drops to 0! Au Hg R 1913 R T Discovery of superconductivity

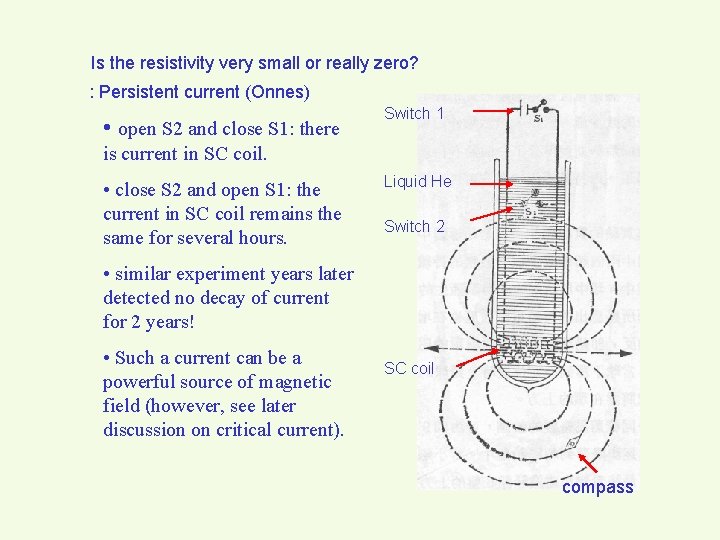
Is the resistivity very small or really zero? : Persistent current (Onnes) • open S 2 and close S 1: there Switch 1 is current in SC coil. • close S 2 and open S 1: the current in SC coil remains the same for several hours. Liquid He Switch 2 • similar experiment years later detected no decay of current for 2 years! • Such a current can be a powerful source of magnetic field (however, see later discussion on critical current). SC coil compass

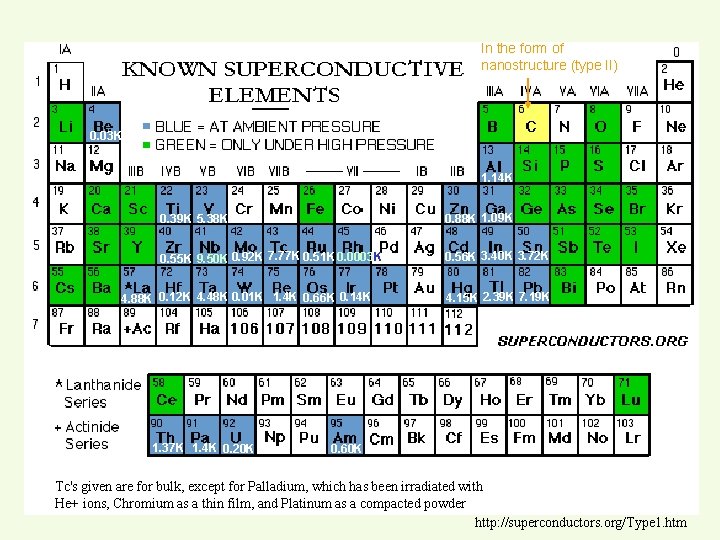
In the form of nanostructure (type II) 0. 03 K 1. 14 K 0. 39 K 5. 38 K 0. 88 K 1. 09 K 0. 55 K 9. 50 K 0. 92 K 7. 77 K 0. 51 K 0. 0003 K 0. 56 K 3. 40 K 3. 72 K 4. 88 K 0. 12 K 4. 48 K 0. 01 K 1. 4 K 0. 66 K 0. 14 K 1. 37 K 1. 4 K 0. 20 K 4. 15 K 2. 39 K 7. 19 K 0. 60 K Tc's given are for bulk, except for Palladium, which has been irradiated with He+ ions, Chromium as a thin film, and Platinum as a compacted powder http: //superconductors. org/Type 1. htm

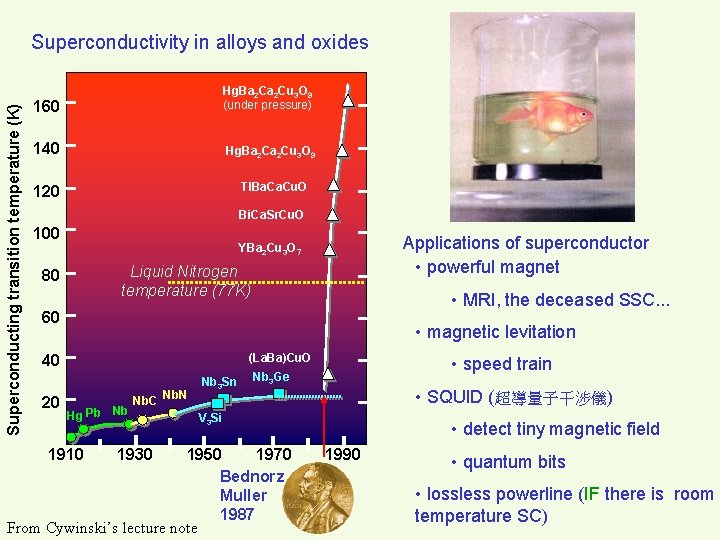
Superconducting transition temperature (K) Superconductivity in alloys and oxides 160 Hg. Ba 2 Cu 3 O 9 (under pressure) 140 Hg. Ba 2 Cu 3 O 9 Tl. Ba. Cu. O 120 Bi. Ca. Sr. Cu. O 100 Applications of superconductor • powerful magnet YBa 2 Cu 3 O 7 Liquid Nitrogen temperature (77 K) 80 • MRI, the deceased SSC. . . 60 • magnetic levitation 40 20 (La. Ba)Cu. O Hg Pb Nb 1910 Nb. C Nb. N 1930 Nb 3 Sn • speed train Nb 3 Ge • SQUID (超導量子干涉儀) V 3 Si 1950 1970 Bednorz Muller 1987 From Cywinski’s lecture note • detect tiny magnetic field 1990 • quantum bits • lossless powerline (IF there is room temperature SC)

• Introduction • Thermal properties • specific heat, entropy, free energy • Magnetic properties • critical field, critical current, Meissner effect, type II SC • London theory of the Meissner effect • penetration length, coherence length, surface energy • Microscopic (BCS) theory • Cooper pair, BCS ground state • Flux quantization • Quantum tunneling • single particle tunneling, DC/AC Josephson effect • SQUID

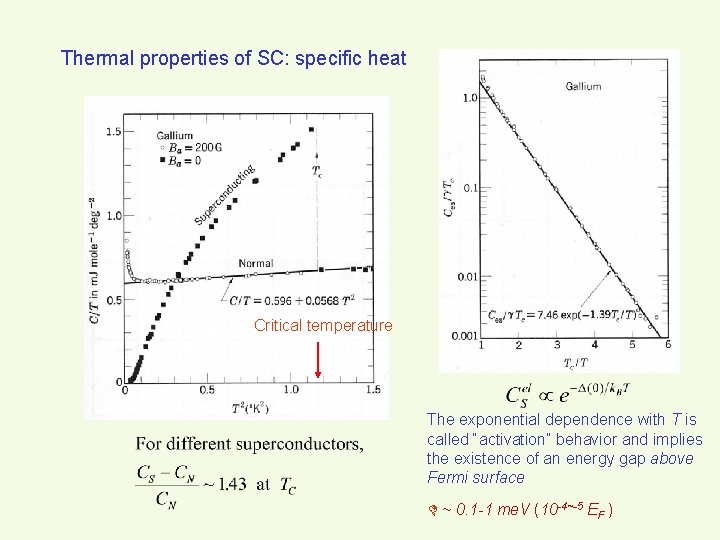
Thermal properties of SC: specific heat Critical temperature The exponential dependence with T is called “activation” behavior and implies the existence of an energy gap above Fermi surface ~ 0. 1 -1 me. V (10 -4~-5 EF )

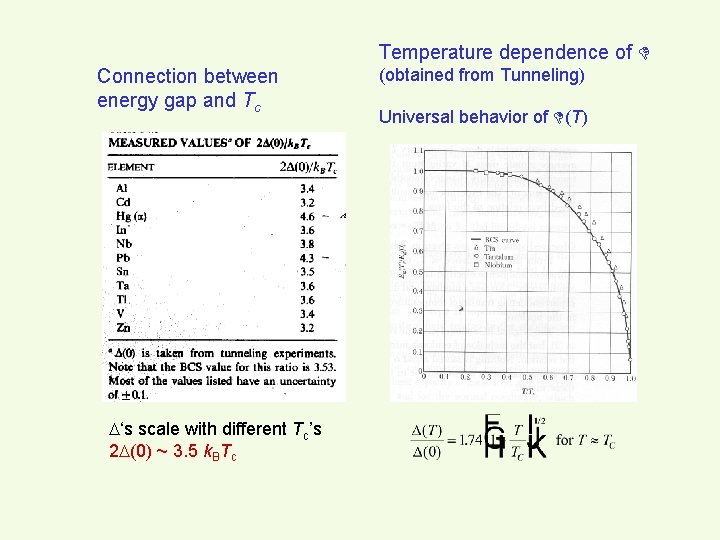
Temperature dependence of Connection between energy gap and Tc ‘s scale with different Tc’s 2 (0) ~ 3. 5 k. BTc (obtained from Tunneling) Universal behavior of (T)

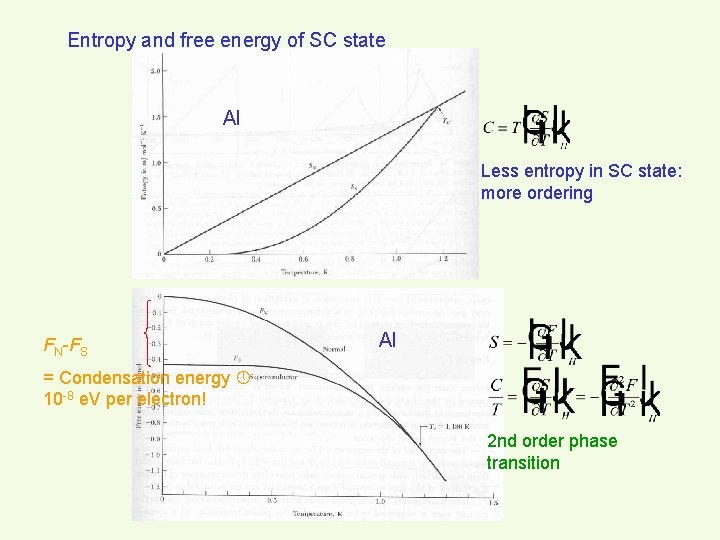
Entropy and free energy of SC state Al Less entropy in SC state: more ordering FN-FS Al = Condensation energy 10 -8 e. V per electron! 2 nd order phase transition

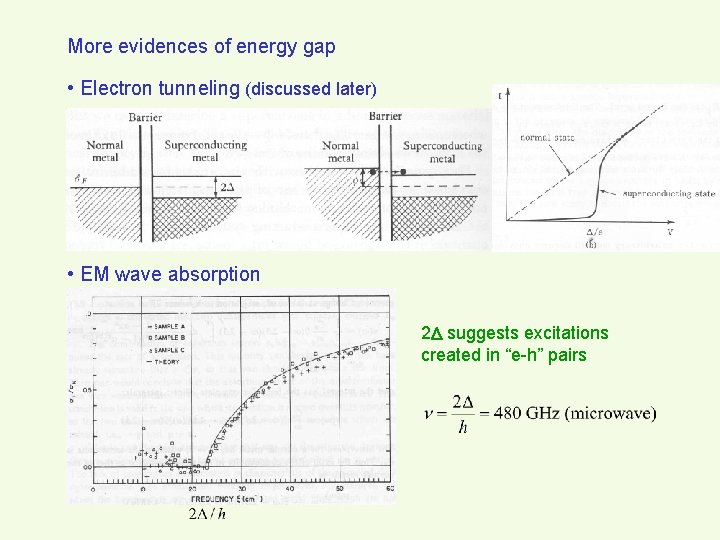
More evidences of energy gap • Electron tunneling (discussed later) • EM wave absorption 2 suggests excitations created in “e-h” pairs

• Introduction • Thermal properties • specific heat, entropy, free energy • Magnetic properties • critical field, critical current, Meissner effect, type II SC • London theory of the Meissner effect • penetration length, coherence length, surface energy • Microscopic (BCS) theory • Cooper pair, BCS ground state • Flux quantization • Quantum tunneling • single particle tunneling, DC/AC Josephson effect • SQUID

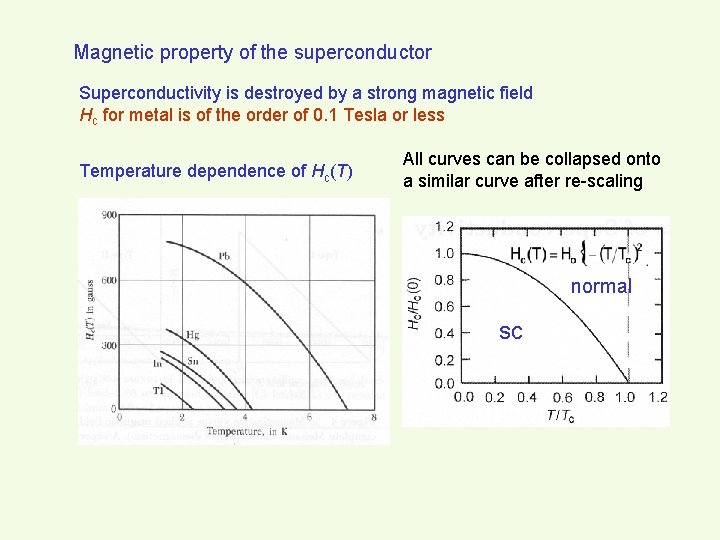
Magnetic property of the superconductor Superconductivity is destroyed by a strong magnetic field Hc for metal is of the order of 0. 1 Tesla or less Temperature dependence of Hc(T) All curves can be collapsed onto a similar curve after re-scaling normal sc

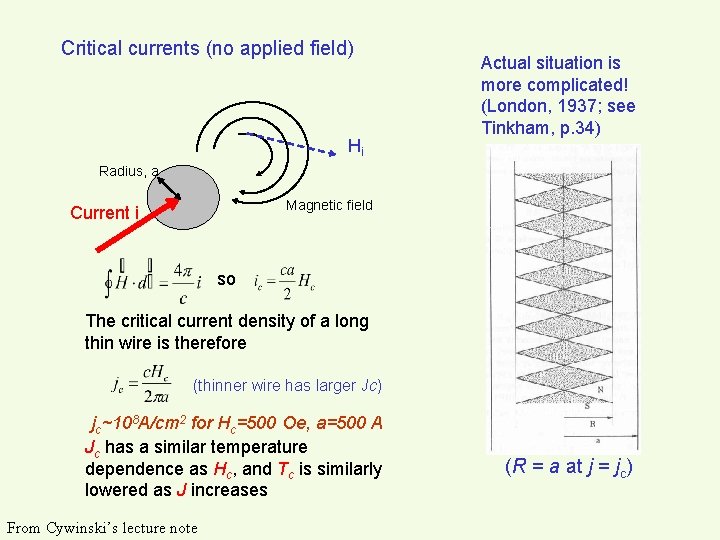
Critical currents (no applied field) Hi Actual situation is more complicated! (London, 1937; see Tinkham, p. 34) Radius, a Magnetic field Current i so The critical current density of a long thin wire is therefore (thinner wire has larger Jc) jc~108 A/cm 2 for Hc=500 Oe, a=500 A Jc has a similar temperature dependence as Hc, and Tc is similarly lowered as J increases From Cywinski’s lecture note (R = a at j = jc)

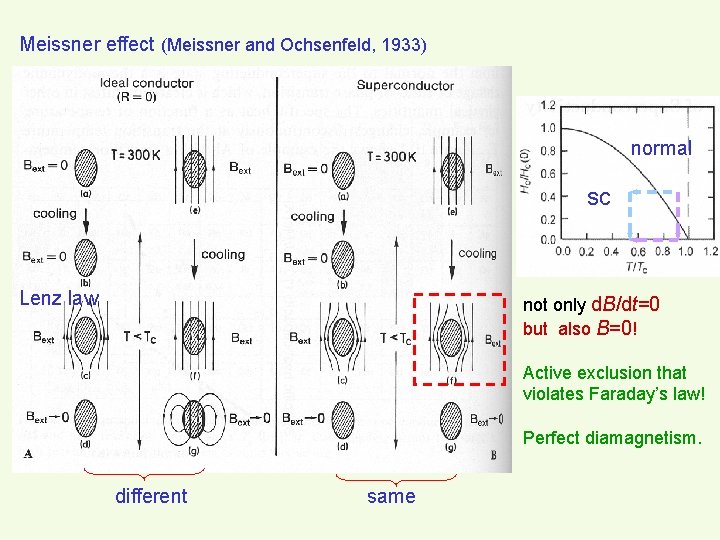
Meissner effect (Meissner and Ochsenfeld, 1933) normal sc Lenz law not only d. B/dt=0 but also B=0! Active exclusion that violates Faraday’s law! Perfect diamagnetism. different same

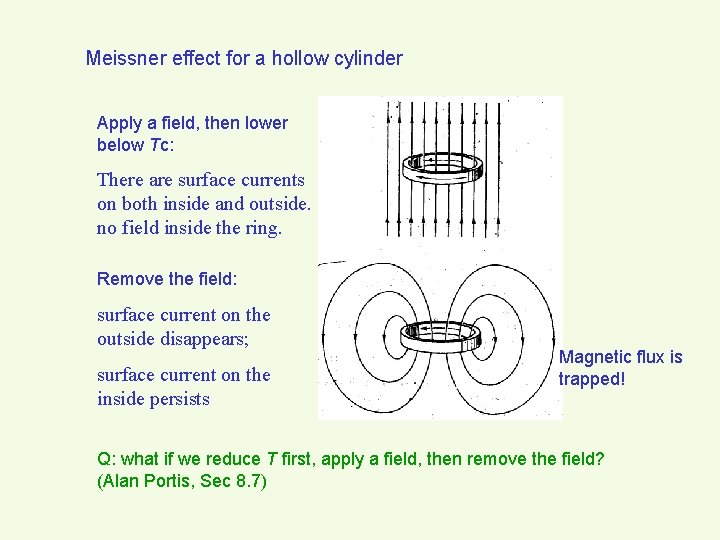
Meissner effect for a hollow cylinder Apply a field, then lower below Tc: There are surface currents on both inside and outside. no field inside the ring. Remove the field: surface current on the outside disappears; surface current on the inside persists Magnetic flux is trapped! Q: what if we reduce T first, apply a field, then remove the field? (Alan Portis, Sec 8. 7)

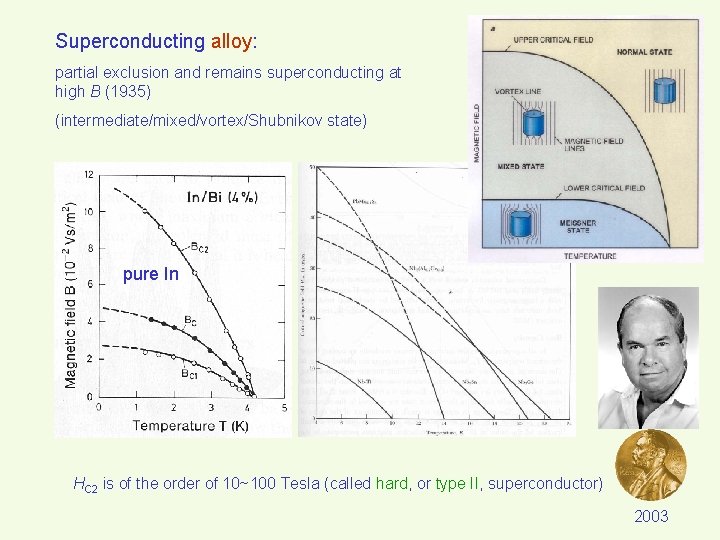
Superconducting alloy: partial exclusion and remains superconducting at high B (1935) (intermediate/mixed/vortex/Shubnikov state) pure In HC 2 is of the order of 10~100 Tesla (called hard, or type II, superconductor) 2003

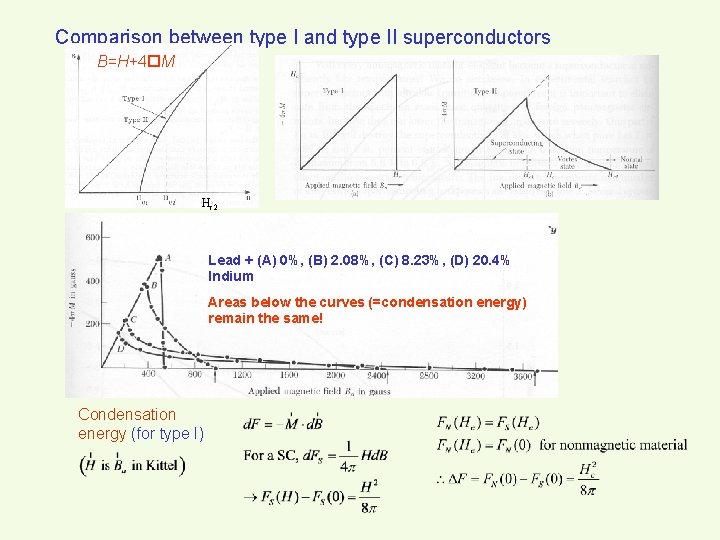
Comparison between type I and type II superconductors B=H+4 M Hc 2 Lead + (A) 0%, (B) 2. 08%, (C) 8. 23%, (D) 20. 4% Indium Areas below the curves (=condensation energy) remain the same! Condensation energy (for type I)

• Introduction • Thermal properties • specific heat, entropy, free energy • Magnetic properties • critical field, critical current, Meissner effect, type II SC • London theory of the Meissner effect • penetration length, coherence length, surface energy • Microscopic (BCS) theory • Cooper pair, BCS ground state • Flux quantization • Quantum tunneling • single particle tunneling, DC/AC Josephson effect • SQUID

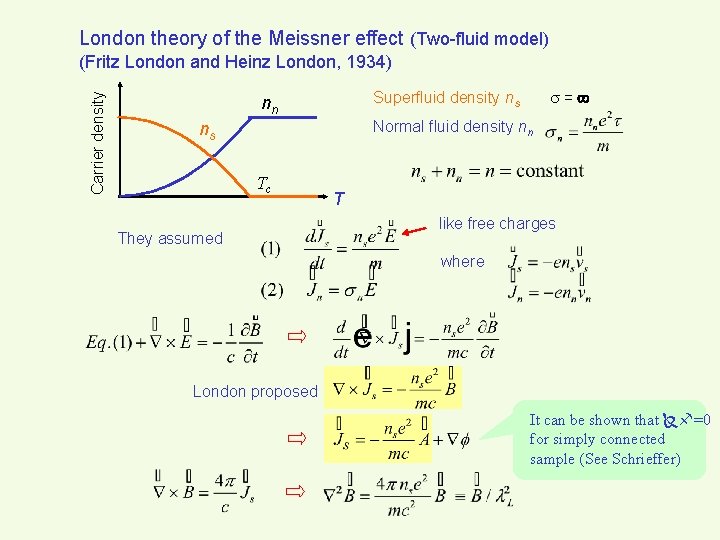
London theory of the Meissner effect (Two-fluid model) Carrier density (Fritz London and Heinz London, 1934) = Superfluid density ns nn Normal fluid density nn ns Tc They assumed T like free charges where London proposed It can be shown that =0 for simply connected sample (See Schrieffer)

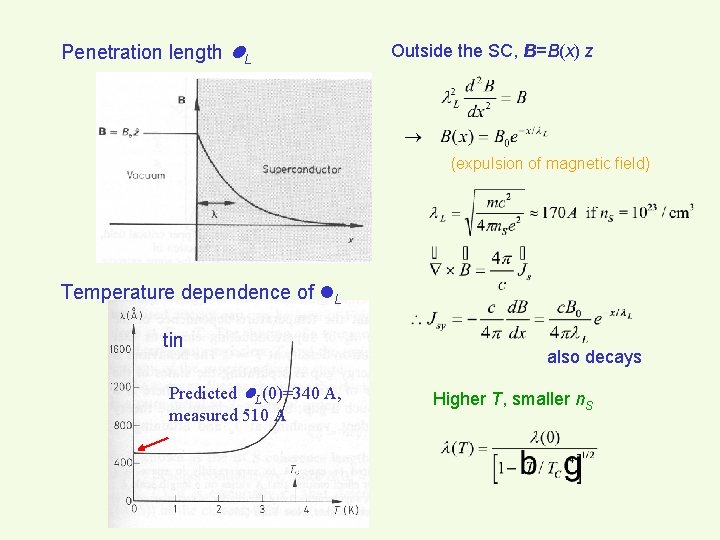
Penetration length L Outside the SC, B=B(x) z (expulsion of magnetic field) Temperature dependence of L tin Predicted L(0)=340 A, measured 510 A also decays Higher T, smaller n. S

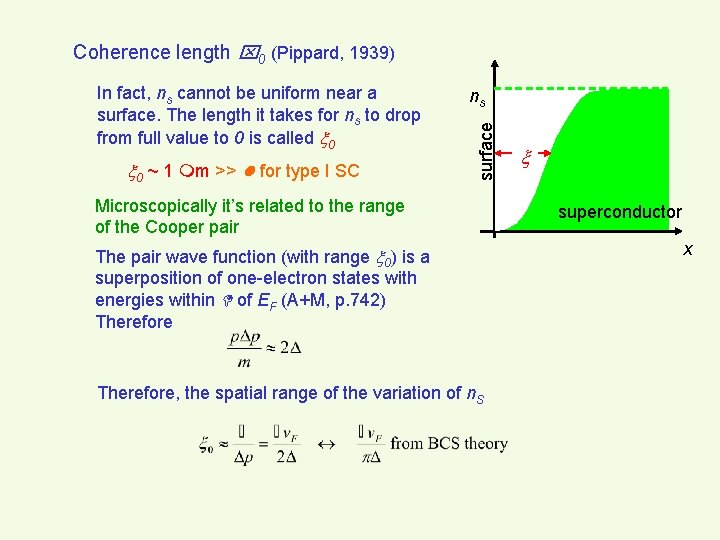
Coherence length 0 (Pippard, 1939) 0 ~ 1 m >> for type I SC ns surface In fact, ns cannot be uniform near a surface. The length it takes for ns to drop from full value to 0 is called 0 Microscopically it’s related to the range of the Cooper pair The pair wave function (with range 0) is a superposition of one-electron states with energies within of EF (A+M, p. 742) Therefore, the spatial range of the variation of n. S superconductor x

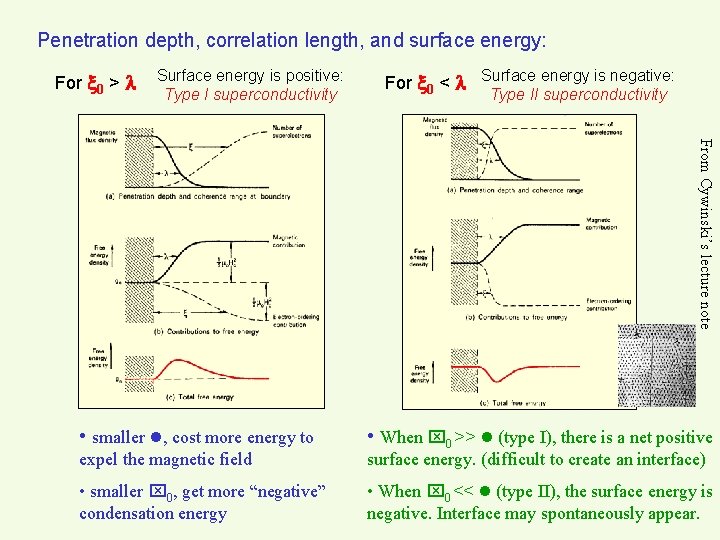
Penetration depth, correlation length, and surface energy: For 0 > Surface energy is positive: Type I superconductivity For 0 < Surface energy is negative: Type II superconductivity From Cywinski’s lecture note • smaller , cost more energy to expel the magnetic field • smaller 0, get more “negative” condensation energy • When 0 >> (type I), there is a net positive surface energy. (difficult to create an interface) • When 0 << (type II), the surface energy is negative. Interface may spontaneously appear.

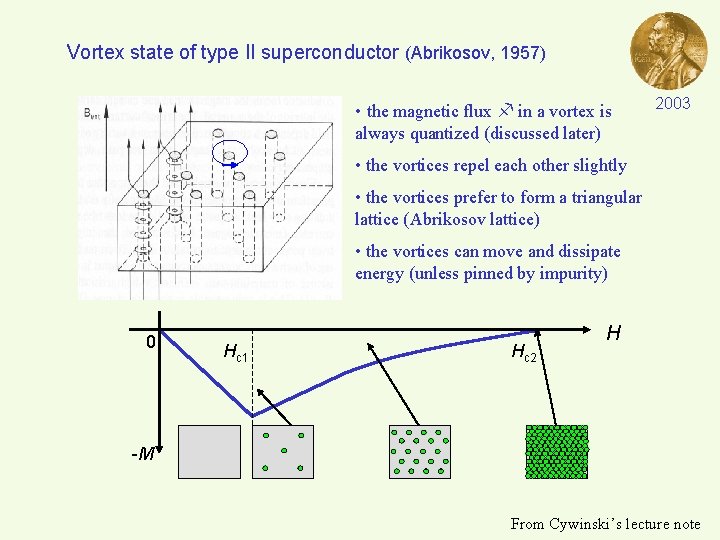
Vortex state of type II superconductor (Abrikosov, 1957) • the magnetic flux in a vortex is always quantized (discussed later) 2003 • the vortices repel each other slightly • the vortices prefer to form a triangular lattice (Abrikosov lattice) • the vortices can move and dissipate energy (unless pinned by impurity) 0 Hc 1 Hc 2 H -M From Cywinski’s lecture note

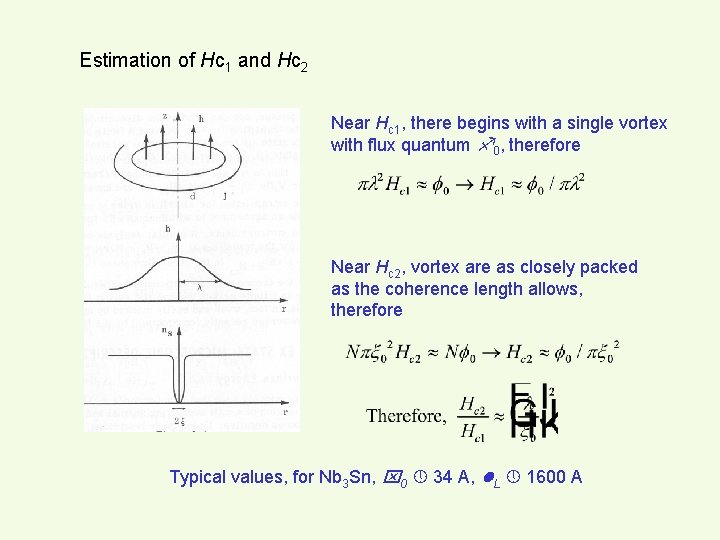
Estimation of Hc 1 and Hc 2 Near Hc 1, there begins with a single vortex with flux quantum 0, therefore Near Hc 2, vortex are as closely packed as the coherence length allows, therefore Typical values, for Nb 3 Sn, 0 34 A, L 1600 A

• Introduction • Thermal properties • specific heat, entropy, free energy • Magnetic properties • critical field, critical current, Meissner effect, type II SC • London theory of the Meissner effect • penetration length, coherence length, surface energy • Microscopic (BCS) theory • Cooper pair, BCS ground state • Flux quantization • Quantum tunneling • single particle tunneling, DC/AC Josephson effect • SQUID

Microscopic picture of the SC state? • Metal X can (cannot) superconduct because its atoms can (cannot) superconduct? Neither Au nor Bi is superconductor, but alloy Au 2 Bi is! White tin can, grey tin cannot! (the only difference is lattice structure) • good normal conductors (Cu, Ag, Au) are bad superconductor, bad normal conductors are good superconductors, why? • Why is the superconducting gap so small? • Failed attempts: polaron, CDW. . . • Isotope effect (1950): It is found that Tc =const M 1/2 for different materials mercury

Brief history of theories of superconductors • 1935 London: superconductivity is a quantum phenomenon on a macroscopic scale. There is a “rigid” (due to the energy gap) superconducting wave function • 1950 • Frohlich: electron-phonon interaction maybe crucial • Reynolds et al, Maxwell: isotope effect • Ginzburg-Landau theory: S can be varied in space. Suggested the connection and wrote down the eq. for (r) (App. I) Difficulty: the condensation energy is 10 8 e. V per electron! 2003 • 1956 Cooper: attractive interaction between electrons (with the help of crystal vibrations) near the FS forms a bound state • 1957 Bardeen, Cooper, Schrieffer: BCS theory • Microscopic wave function for the condensation of Cooper pairs Ref: 1972 Nobel lectures by Bardeen, Cooper, and Schrieffer 1972

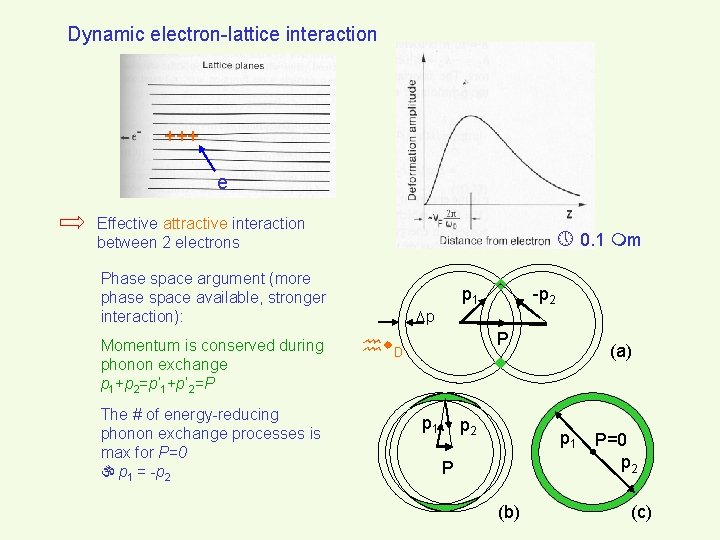
Dynamic electron-lattice interaction +++ e Effective attractive interaction between 2 electrons 0. 1 m Phase space argument (more phase space available, stronger interaction): Momentum is conserved during phonon exchange p 1+p 2=p’ 1+p’ 2=P The # of energy-reducing phonon exchange processes is max for P=0 p 1 = -p 2 p 1 p -p 2 P D p 1 p 2 (a) p 1 P (b) P=0 p 2 (c)

Cooper pair (Cooper, 1956) 2 electrons with opposite momenta (p , -p ) can form a bound state with binding energy (the spin is opposite by Pauli principle) • Fraction of electrons involved k. Tc/EF 10 -4 • Average spacing between condensate electrons 10 nm 2 (0) ~ 3. 5 k. BTc • Therefore, within the volume occupied by the Cooper pair, there approximately (0. 1 m/10 nm)3 103 other pairs. • These pairs (similar to bosons) are highly correlated and form a macroscopic condensate state BCS with (non-perturbative result!) Schafroth (1951): Meisner effect cannot be obtained in any finite order of perturbation. Migdal (1958): no energy gap from the perturbation theory. • Electrons within k. TC of the FS have their energy lowered by the order of k. TC in the condensation (therefore 10 -8 e. V per electron).

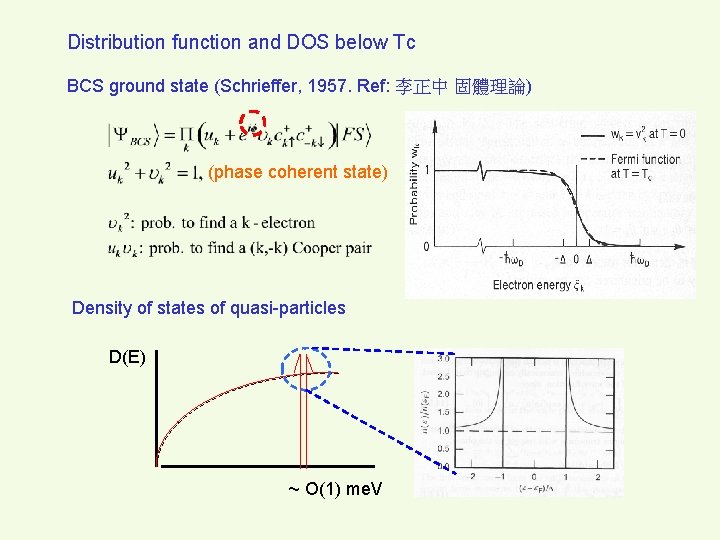
Distribution function and DOS below Tc BCS ground state (Schrieffer, 1957. Ref: 李正中 固體理論) (phase coherent state) Density of states of quasi-particles D(E) ~ O(1) me. V

• Introduction • Thermal properties • specific heat, entropy, free energy • Magnetic properties • critical field, critical current, Meissner effect, type II SC • London theory of the Meissner effect • penetration length, coherence length, surface energy • Microscopic (BCS) theory • Cooper pair, BCS ground state • Flux quantization • Quantum tunneling • single particle tunneling, DC/AC Josephson effect • SQUID

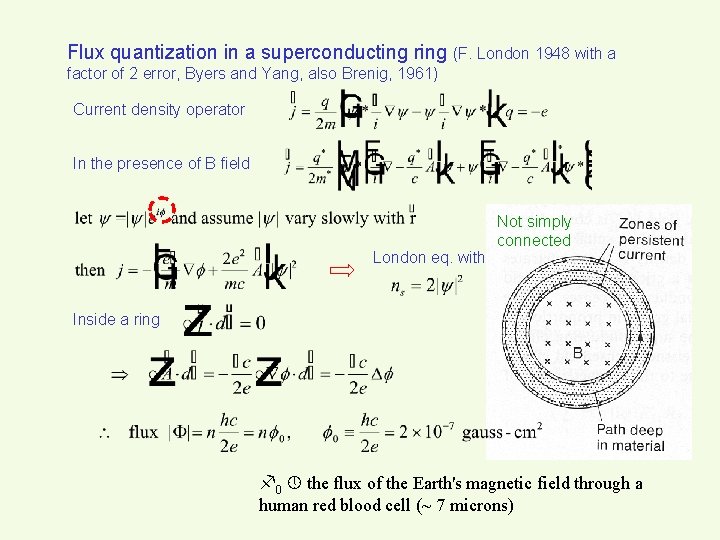
Flux quantization in a superconducting ring (F. London 1948 with a factor of 2 error, Byers and Yang, also Brenig, 1961) Current density operator In the presence of B field London eq. with Not simply connected Inside a ring 0 the flux of the Earth's magnetic field through a human red blood cell (~ 7 microns)

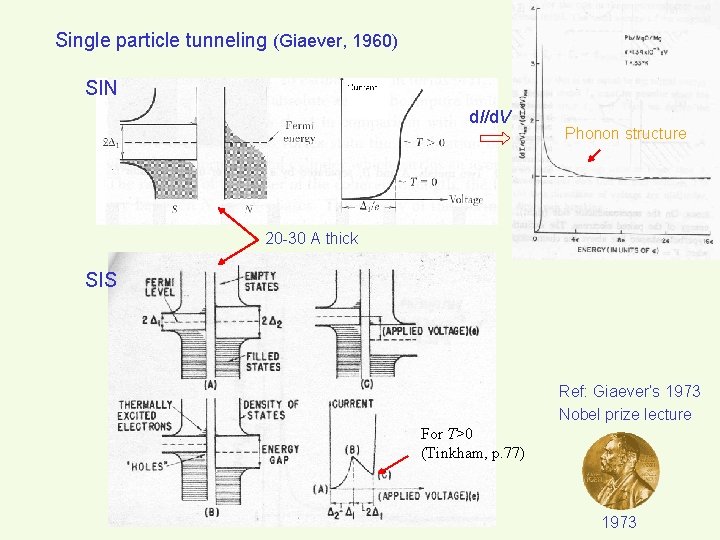
Single particle tunneling (Giaever, 1960) SIN d. I/d. V Phonon structure 20 -30 A thick SIS Ref: Giaever’s 1973 Nobel prize lecture For T>0 (Tinkham, p. 77) 1973

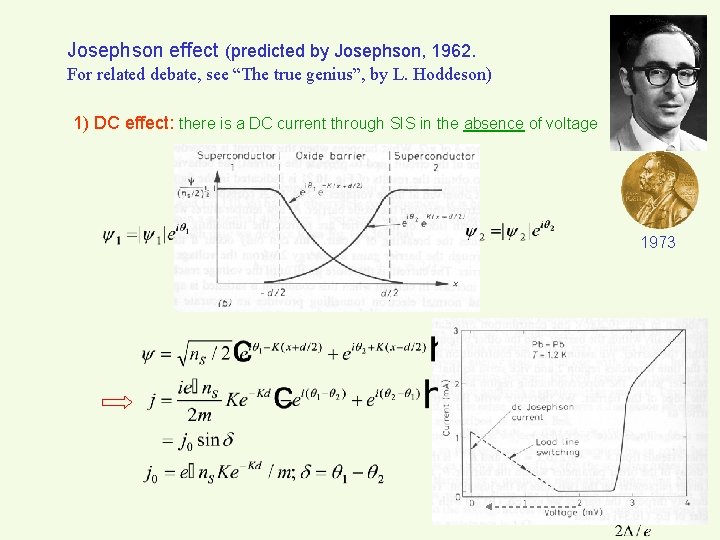
Josephson effect (predicted by Josephson, 1962. For related debate, see “The true genius”, by L. Hoddeson) 1) DC effect: there is a DC current through SIS in the absence of voltage 1973

2) AC Josephson effect apply a DC voltage, then there is a rf current oscillation • An AC supercurrent of Cooper pairs with freq. =2 e. V/h, a weak microwave is generated. • can be measured very accurately, so tiny V as small as 10 -15 V can be detected. • Also, since V can be measured with accuracy about 1 part in 1010, so 2 e/h can be measured accurately. • JJ-based voltage standard (1990): 1 V the voltage that produces a frequency of 483, 597. 9 GHz (exact). • advantage: independent of material, lab, time (similar to the quantum Hall standard)

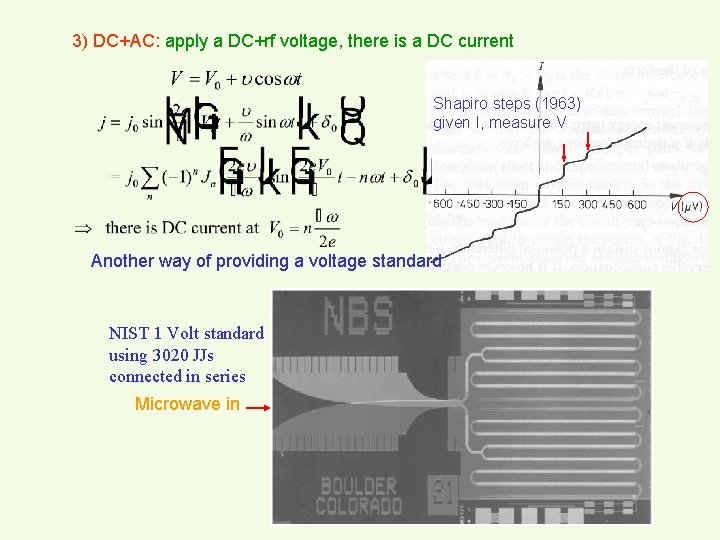
3) DC+AC: apply a DC+rf voltage, there is a DC current Shapiro steps (1963) given I, measure V Another way of providing a voltage standard NIST 1 Volt standard using 3020 JJs connected in series Microwave in

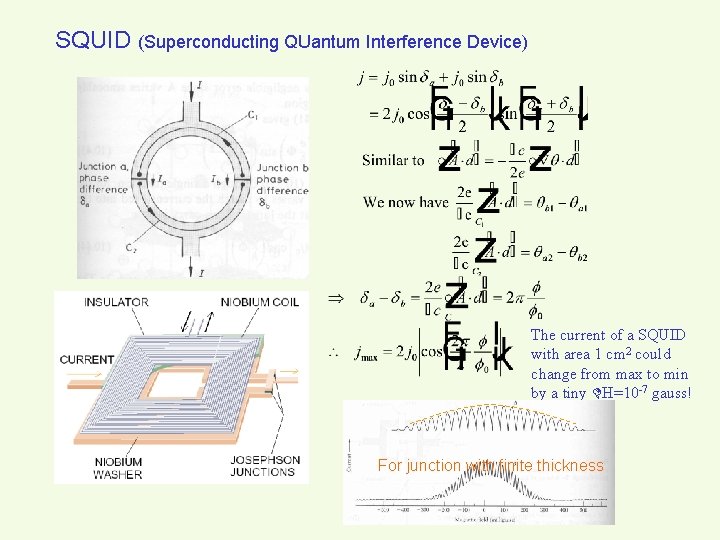
SQUID (Superconducting QUantum Interference Device) The current of a SQUID with area 1 cm 2 could change from max to min by a tiny H=10 -7 gauss! For junction with finite thickness

Super. Conducting Magnet Non-destructive testing MCG, magnetocardiography MEG, magnetoencephlography

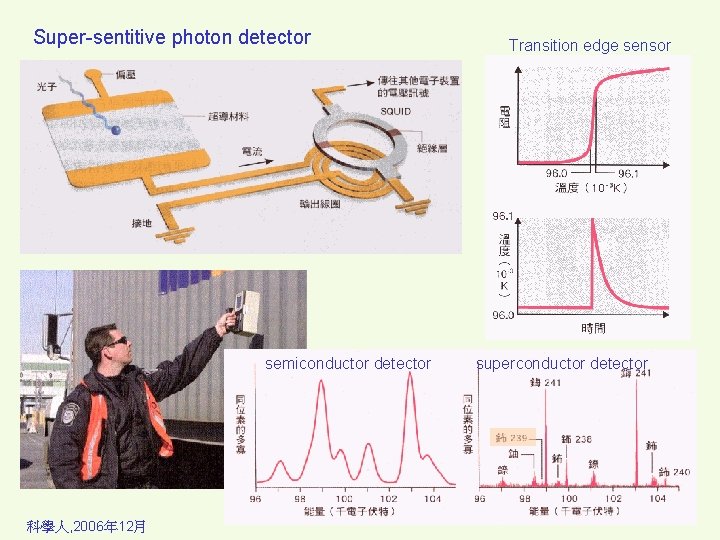
Super-sentitive photon detector semiconductor detector 科學人, 2006年 12月 Transition edge sensor superconductor detector