Summing the Instantons in the Heterotic String Jock

Summing the Instantons in the Heterotic String Jock Mc. Orist University of Chicago 0712. 3272, 0810. 0012 with Ilarion Melnikov October 28 th, Rutgers University Rutgers, October 28 th, 2008 Jock Mc. Orist

Motivation: What and Why? What do we want to study? …. Phenomenology … Why? Gratuitous LHC Pic Rutgers, October 28 th, 2008 Jock Mc. Orist 2

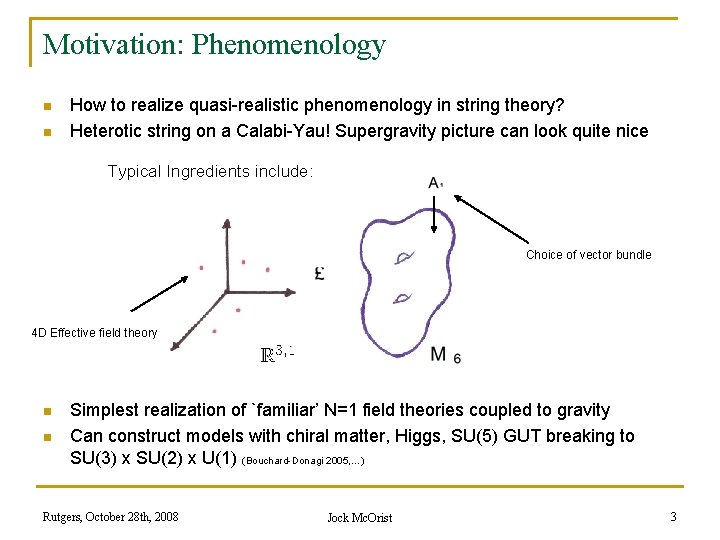
Motivation: Phenomenology n n How to realize quasi-realistic phenomenology in string theory? Heterotic string on a Calabi-Yau! Supergravity picture can look quite nice Typical Ingredients include: Choice of vector bundle 4 D Effective field theory n n Simplest realization of `familiar’ N=1 field theories coupled to gravity Can construct models with chiral matter, Higgs, SU(5) GUT breaking to SU(3) x SU(2) x U(1) (Bouchard-Donagi 2005, …) Rutgers, October 28 th, 2008 Jock Mc. Orist 3

Motivation: Quantum corrections? n Approaches limited to supergravity…. String scale cycle size: lots of string corrections SUGRA valid if ls << R What if a cycle approaches string scale? Need a string description! n n How does one compute in a string description? Restrict to Heterotic on a Calabi-Yau. Low energy physics then depends on the topology and choice of vector bundle Rutgers, October 28 th, 2008 Jock Mc. Orist 4

Motivation: Easy Example n For the standard embedding n Spacetime low energy effective field theory: q n Unbroken answer is well-known gauge group, and matter multiplets, moduli Worldsheet theory is a (2, 2) SCFT q Can compute and Yukawa couplings, mirror symmetry, special geometry Y = Yukawa couplings n (2, 2) SCFTs are highly non-generic. What can we say about general choices of bundle? (i. e. phenomenologically realistic theories) Rutgers, October 28 th, 2008 Jock Mc. Orist 5

Motivation: Generic Compactifications n Worldsheet theory is a (0, 2) SCFT n Not known how to compute quantum corrections in many (0, 2) theories. Lots of open questions: q q n What is the moduli space of (0, 2) SCFTs? Where are the SCFTs singular? What are the Yukawa couplings? Is there a notion of heterotic mirror symmetry? Is there special geometry? We answer some of these questions for (0, 2) models where deformation from TV Rutgers, October 28 th, 2008 Jock Mc. Orist small 6

Motivation: What do we really know? n We really only understand a small slice of the Heterotic moduli space! Bundle Rank Gauge Group (2, 2) locus ? Rank 3 ? Rank 4 Today, we’ll explore here ? Future Work Rank 5 ? Theme of our results: What works for (2, 2) works for (0, 2) Rutgers, October 28 th, 2008 Jock Mc. Orist 7

Outline 1. Motivation: How much do we know about the Heterotic String? 2. (0, 2) GLSMs 3. A/2 -Twist V-Model (toric varieties – a good warm-up) 4. A/2 -Twist M-Model (Calabi-Yau’s – Yukawa couplings) 5. B/2 -Twist M-Model (LG theories) 6. Summary & Conclusion Rutgers, October 28 th, 2008 Jock Mc. Orist 8

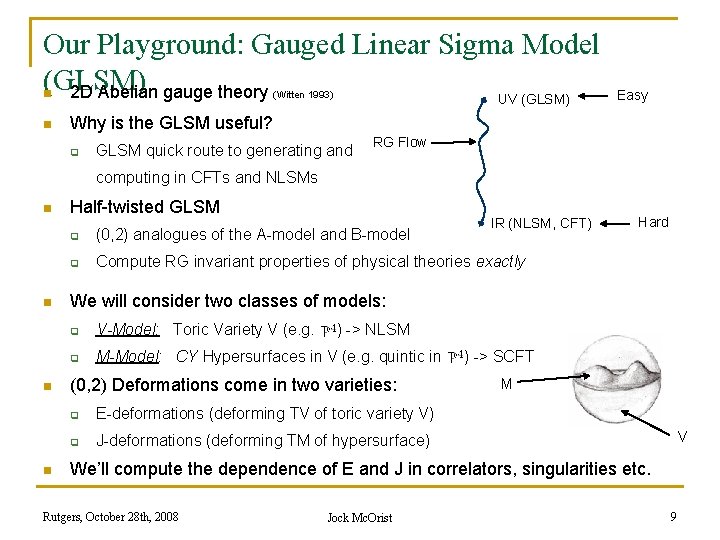
Our Playground: Gauged Linear Sigma Model (GLSM) n 2 D Abelian gauge theory UV (GLSM) (Witten 1993) n Easy Why is the GLSM useful? q GLSM quick route to generating and RG Flow computing in CFTs and NLSMs n n Half-twisted GLSM IR (NLSM, CFT) q (0, 2) analogues of the A-model and B-model q Compute RG invariant properties of physical theories exactly Hard We will consider two classes of models: q V-Model: Toric Variety V (e. g. ) -> NLSM q M-Model: CY Hypersurfaces in V (e. g. quintic in (0, 2) Deformations come in two varieties: q E-deformations (deforming TV of toric variety V) q J-deformations (deforming TM of hypersurface) ) -> SCFT M V We’ll compute the dependence of E and J in correlators, singularities etc. Rutgers, October 28 th, 2008 Jock Mc. Orist 9

Review of (2, 2)-GLSM n The (2, 2) GLSM has an action q q q U(1)r Abelian gauge theory (a = 1, …, r) parameterize target space with i=1, …, n FI parameters Kähler moduli (size or volume of space) W = 0: target space is toric variety (V-model) W 0: superpotential induces a hypersurface (M-model) M V Rutgers, October 28 th, 2008 Jock Mc. Orist 10

Review of (0, 2) GLSM n n Consider (0, 2) theories with a (2, 2) locus Field content easily understood by decomposing (2, 2) fields: Bosons (2, 2) Field Fermions Matter fields Vector multiplet left- or right-moving Field Strength toric variety V & n q q n bundle Bundle fermions obey a constraint: E determines the behavior of the bundle Holomorphic function Gives rise to (0, 2) deformations. For example (2, 2) n Left-moving heterotic fermions (0, 2) Matrix of complex parameters specifying bundle These are the E-deformations. Now let’s compute correlators… Rutgers, October 28 th, 2008 Jock Mc. Orist 11

Outline 1. Motivation: How much do we know about the Heterotic String? 2. (0, 2) GLSMs 3. A/2 -Twist V-Model (toric varieties – a good warm-up) 4. A/2 -Twist M-Model (Calabi-Yau’s – Yukawa couplings) 5. B/2 -Twist M-Model (LG theories) 6. Summary & Conclusion Rutgers, October 28 th, 2008 Jock Mc. Orist 12

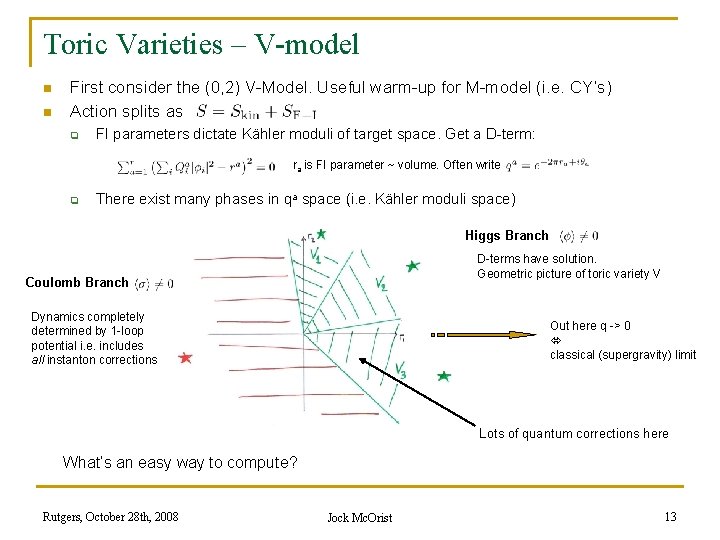
Toric Varieties – V-model n n First consider the (0, 2) V-Model. Useful warm-up for M-model (i. e. CY’s) Action splits as q FI parameters dictate Kähler moduli of target space. Get a D-term: ra is FI parameter ~ volume. Often write q There exist many phases in qa space (i. e. Kähler moduli space) Higgs Branch D-terms have solution. Geometric picture of toric variety V Coulomb Branch Dynamics completely determined by 1 -loop potential i. e. includes all instanton corrections Out here q -> 0 classical (supergravity) limit Lots of quantum corrections here What’s an easy way to compute? Rutgers, October 28 th, 2008 Jock Mc. Orist 13

A/2 -Twisted V-Model: An Easy Route to Correlators n For (2, 2)-theories, can do an A-twist q q q n q q For (0, 2) theories, can do A/2 -twist q q BRST operator Cohomology elements are still σ (Adams, Distler et al, …) q Theory not topological. But is conformal => observables RG invariant n Localization still applies (Melnikov-Sethi 2007) n Do the two methods still apply? Perturbative corrections cancel Semi-classical analysis arbitrarily good Two methods: q n BRST operator Cohomology elements correspond to (1, 1)-classes on V. Label them σ fields. Stress Energy tensor is BRST exact => observables are RG invariant Correlators may be computed by localization q n n * Higgs Branch: Summing gauge instantons Coulomb branch: 1 -loop potential How does this change for (0, 2)? q q n If so, some more questions: q q Rutgers, October 28 th, 2008 Jock Mc. Orist Higgs Branch Coulomb Branch Where are correlators singular? What is their moduli dependence? 14

Review: Summing Gauge Instantons on (2, 2) n n First technique: Higgs phase (Morrison-Plesser 1995) General considerations imply correlator given by sum over gauge instantons Kähler parameters n Compute term-by-term in the instanton expansion. Use localization: q Correlators reduce to integration over zero modes Straightforward to compute using toric geometry n map to (1, 1)-classes on , the space of zero modes Matter fields are holomorphic maps of degree Moduli space of maps is a toric variety: n Euler class for obstruction bundle n n Rutgers, October 28 th, 2008 Jock Mc. Orist 15

A/2 V-Model: Summing Gauge Instantons on (0, 2) n n For (0, 2) theories story is much the same Answer looks like: Now “sheafy” type objects. Hard? Guffin-Katz 2007… n n n GLSM naturally generates toric like structures => should be an analogue of toric-like methods to compute this integral Inspired by the (0, 2) GLSM, we conjecture precisely these “toric” methods for (0, 2) theories. For example, (0, 2) (2, 2) Bundle parameters q q Works in number of examples Avoids complications of sheaves and computations are combinatoric Rutgers, October 28 th, 2008 Jock Mc. Orist 16

A/2 V-Model: Coulomb Branch n n Second technique: Coulomb Branch (Mc. Orist-Melnikov 2007) Simple algebraic technique. Instantons are summed automatically fields get massive and can be integrated out Dynamics completely determined by 1 -loop superpotential ‘t Hooft anomaly matching and holomorphy implies 1 -loop result is exact n Correlators may be evaluated by localization sum over Coulomb vacua n (0, 2) parameters Reproduces answer computed on Higgs branch Rutgers, October 28 th, 2008 Jock Mc. Orist 17

Example: Resolved n n Compute by Coulomb branch technique and gauge instanton sum For example: Get instanton expansion by expanding in powers of qa are E-deformation parameters n Interesting singularity structure: q D Kähler singularity. Familiar from (2, 2) q Bundle singularity. Visible even when q -> 0 (large radius limit) n n n Correspond to fields becoming light In (0, 2) parameter space -> find a new branch (mixed Coulomb-Higgs) Example of new structures present in the Heterotic bundle moduli space Rutgers, October 28 th, 2008 Jock Mc. Orist 18

Outline 1. Motivation: How much do we know about the Heterotic String? 2. (0, 2) GLSMs 3. A/2 -Twist V-Model 4. A/2 -Twist M-Model (Calabi-Yau’s – Yukawa couplings) 5. B/2 -Twist M-Model (LG theories) 6. Summary & Conclusion Rutgers, October 28 th, 2008 Jock Mc. Orist 19

M-Model: Hypersurfaces & Calabi-Yau’s n To construct a Calabi-Yau, we add two additional multiplets on a superpotential term: . Then turn J M for (2, 2) n Vacua: q q n D-terms => matter fields parameterize V F-terms => Imply constraints (e. g. P = 0). Defines a hypersurface J functions give second type of (0, 2)-deformations: (2, 2) q n E V (0, 2) J-deformations (quintic) J-deformations correspond geometrically to wiggling the hypersurface bundle To summarize (0, 2)-deformations in M-model: q q E-deformations from V J-deformations from hypersurface Rutgers, October 28 th, 2008 Jock Mc. Orist 20

A-Twist of M-Model (CY Hypersurface) n n With (2, 2)-supersymmetry the M-model admits an A-twist Similar to V-Model (toric variety): q q n Some important twists: q q n n n cohomology given by pullbacks of Localization still works: correlators reduce to an integration over moduli space Selection rule implies compute 3 -point functions => Yukawa’s Vacuum equations are those of the V-model with additional constraints e. g. P=0 Defines a locus. Tricky to compute gauge instantons on (as opposed to which is toric) Looks hard to compute correlators in conformal models… All is not lost! Superpotential is exact. Correlators independent of details of the hypersurface (i. e. complex structure moduli) Implies M-model correlators (hard) may be related to V-model correlators (easy). Made precise by the Quantum Restriction Formula: (Morrison-Plesser 1995) Computations now simple! Does this work for (0, 2) theories? Rutgers, October 28 th, 2008 Jock Mc. Orist 21

M-Model: Quantum Restriction Formula for (0, 2) n n We show the same works for (0, 2) Some a priori considerations: n (0, 2) Supersymmetry => only BRST exact. Are correlators independent of all J-parameters? (e. g. may be holomorphic J dependence? ) n Does the Quantum Restriction Formula still apply? (M-model correlators reduce to V-model correlators? ) n However, by carefully integrating out n n fields, we show is BRST exact => does not formally affect correlators. Can take the limit which implies As the moduli space & worldsheet are compact, this will not affect large field asymptotics n Summing over instantons, we get Quantum Restriction Formula for (0, 2) theories n Important feature: J dropped out => A/2 -twisted theory is independent of complex structure and J-deformations! Rutgers, October 28 th, 2008 Jock Mc. Orist 22

M-Model: Quantum Restriction Formula n Additional comments: q q n Related a M-model correlator (hard) to a V-model correlator (easy) This gives rise to unnormalized Yukawa couplings in the SCFT Can be easily extended to Complete Intersection Calabi-Yau’s in toric varieties Independence of J-deformations is important for any mirror symmetry considerations Let’s compute an example…. Rutgers, October 28 th, 2008 Jock Mc. Orist 23

M-Model Example: CY Hypersurface in resolved n Same example consider previously. Hypersurface defined using a superpotential W. On the (2, 2) locus W is: n Applying our V-model techniques and Quantum Restriction we get n Interesting features: q q q Yukawas: Kähler and bundle moduli mixing -> treated on the same footing Large volume limit q -> 0 -- still can get bundle moduli singularities Easy to parameterize locus of points where SCFT is singular: (0, 2) (2, 2) Rutgers, October 28 th, 2008 Jock Mc. Orist 24

Outline 1. Motivation: How much do we know about the Heterotic String? 2. (0, 2) GLSMs 3. A/2 -Twist V-Model (toric varieties – a good warm-up) 4. A/2 -Twist M-Model (Calabi-Yau’s – Yukawa couplings) 5. B/2 -Twist M-Model (LG theories) 6. Summary & Conclusion Rutgers, October 28 th, 2008 Jock Mc. Orist 25

B/2 -Twisted M-Model (CY Hypersurface) n n M-Model admits a B/2 -twist On (2, 2)-locus the B-Model has the following features: (Witten 1993) q q n BRST invariance => independent of Kähler parameters & no quantum corrections Correlators depend holomorphically on complex structure moduli Observables correspond to monomials in the superpotential e. g. Correlators compute Yukawa couplings We show these features persist for a large class of (0, 2)-models: q q q Fermion zero mode analysis => most models have no quantum corrections In addition, if there is a Landau-Ginzburg phase (eg. quintic and ): n Correlators do not depend E-deformations n Reduce to a Landau-Ginzberg computation, exactly as on the (2, 2)-locus Some models can not be ruled out from having instanton corrections Rutgers, October 28 th, 2008 Jock Mc. Orist 26

B/2 -Twisted Model: Quantum Corrections? n An example of a smooth M-model that is not ruled out by the zero-mode analysis. Charge matrix with polynomial n Further work is needed. Related work is suggestive Rutgers, October 28 th, 2008 Jock Mc. Orist (Sharpe 2006) 27

B/2 -Twisted M-Model: Hypersurface in Resolved n Do an example. This will be illustrative of how things work in general M-model for Resolved. Is independent of quantum corrections. Landau-Ginzburg phase: n Consider n Take n Performing some field redefinitions, we show n In particular, the E-parameters drop out of the correlator! Thus, the B/2 - theory depends only on complex structure and J-deformations n n Rutgers, October 28 th, 2008 where , e. g. Expanding Jock Mc. Orist Yukawa couplings deep in the LG phase 28

Outline 1. Motivation: How much do we know about the Heterotic String? 2. (0, 2) GLSMs 3. A/2 -Twist V-Model (toric varieties – a good warm-up) 4. A/2 -Twist M-Model (Calabi-Yau’s – Yukawa couplings) 5. B/2 -Twist M-Model (LG theories) 6. Summary & Conclusion Rutgers, October 28 th, 2008 Jock Mc. Orist 29

A/2 -Twisted and B/2 -Twisted Models: Mirrors? n On the (2, 2)-locus there is a well-developed notion of mirror symmetry. In the language of the GLSM it is quite pretty: A-twisted M-model q B-twisted W-model M and W are mirror Calabi-Yaus. Can be easily constructed via toric geometry (Batyrev, 1993, Borisov 1994) Kähler moduli of M q n n complex structure moduli of W In the GLSM this is the ‘monomial-divisor mirror-map’ (Morrison-Plesser 1995, …) The results we’ve obtained here are suggestive of a natural generalization to (0, 2) theories: A/2 -twisted M-model B/2 -twisted W-model Kähler + E-deformations Complex structure + J-deformations Is there a mirror map? Rutgers, October 28 th, 2008 Jock Mc. Orist 30

Summary and Future Work n n n We’ve explored some aspects of (0, 2)-theories using half-twists (0, 2)-theories are eminently computable It is easy to compute Yukawa couplings in a range of models via: q q n We find the moduli space splits in a nice way: q q n Quantum Restriction Formula via A/2 -twist Classical Intersection Theory via B/2 -twist Important for Phenomenology of the Heterotic string (Kähler + E-deformations) (Complex Structure + J-deformations) Interesting bundle singularities Many future directions q q q Count (0, 2)-deformations of known (2, 2)-mirror pairs. Do they match in any sensible way? Is there a generalization of the GLSM mirror map? Compute Kähler potential for the matter and moduli fields (normalize couplings). Is there a generalization of special geometry? The most phenomenologically interesting vacua are rank 4 and rank 5 bundles. Does our analysis extend to these theories? Rutgers, October 28 th, 2008 Jock Mc. Orist 31

Outline 1. Motivation: How much do we know about the Heterotic String? 2. (0, 2) GLSMs 3. A/2 -Twist V-Model (toric varieties – a good warm-up) 4. A/2 -Twist M-Model (Calabi-Yau’s – Yukawa couplings) 5. B/2 -Twist M-Model (LG theories) 6. Summary & Conclusion Rutgers, October 28 th, 2008 Jock Mc. Orist 32