Summary w Prediction n n regression analysis comparing

Summary w Prediction n n regression analysis comparing means w Statistical inference n significance

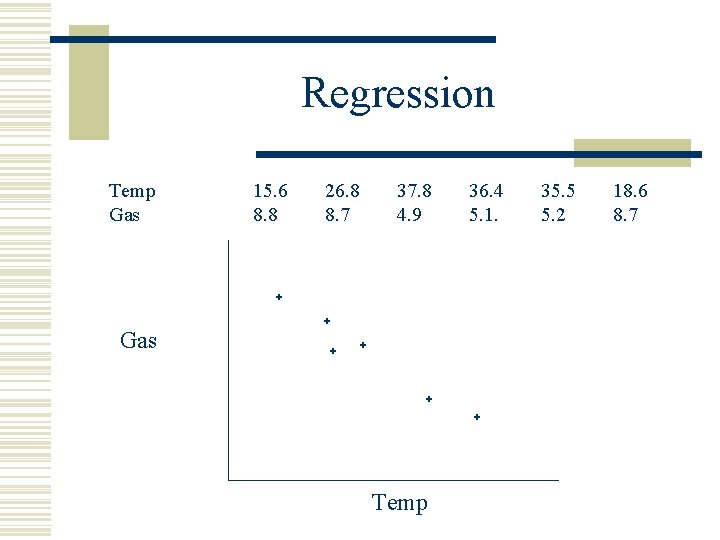
Regression Temp Gas 15. 6 8. 8 26. 8 8. 7 37. 8 4. 9 Gas Temp 36. 4 5. 1. 35. 5 5. 2 18. 6 8. 7

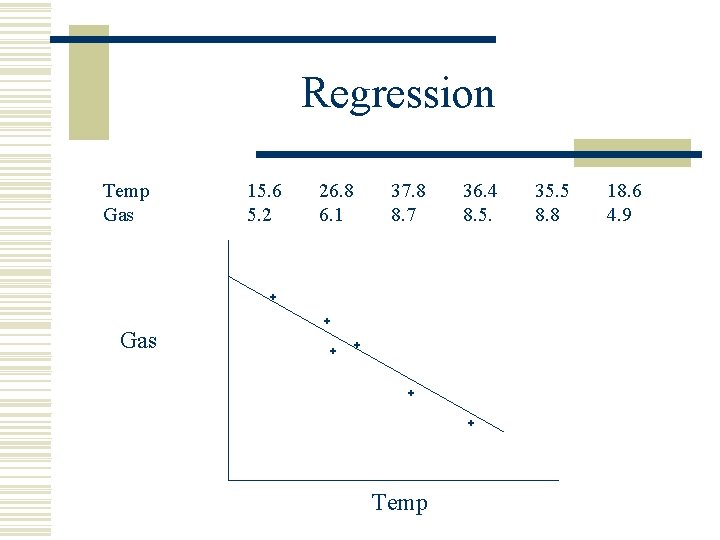
Regression Temp Gas 15. 6 5. 2 26. 8 6. 1 37. 8 8. 7 Gas Temp 36. 4 8. 5. 35. 5 8. 8 18. 6 4. 9

Regression equation Dependent variable Slope Independent variable Y intercept Substitute x value into the equation and calculate the value of y.

Regression w Prediction using regression is most secure when the independent variable x takes a value within the range of the x values in your data n not about cause and effect w extrapolation n n Using the regression equation for prediction outside the range of the original data less secure

R 2: the Coefficient of Determination w Link between correlation and regression w tells us the proportion of the variance of one variable that can be explained by straight line dependence on the other variable w How much can we rely on the regression estimates

R 2: the Coefficient of Determination n . 892 =. 79 l l n 79% of the variance in first year uni marks can be accounted for by the variance in the sample’s SAT scores 21% of the variance in first year marks is accounted for by other unknown variables Eg 2. the correlation between length of car and mpg/l is -. 7 l l Interpret in terms of r 2 percent of variance in the Y scores variable which is associated with the variance in the X scores.

Regression w Use when. . . n n n 1. both the variables are interval 2. for prediction about the scores of individual cases or groups 3. to measure the amount of impact or change that one variable produces in another

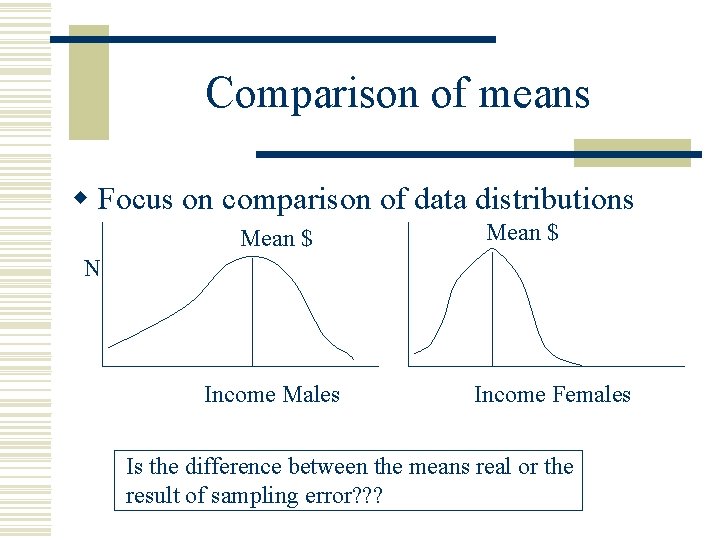
Comparison of means w Focus on comparison of data distributions Mean $ N Income Males Income Females Is the difference between the means real or the result of sampling error? ? ?

Comparison of means w Appropriate when. . n n n Dependent variable is interval independent variable has few categories (2 or 3) initial analysis l look for patterns then use tables

Statistical significance w “Real” or “Chance”? w Significance n n judgements that are made according to agreed on mathematical rules of probability used to infer observed differences or relationships in the sample to the population studied

Statistical significance w If we drew 100 samples, how likely is it that we would get a faulty one w Probability theory n provides us an estimate of how likely it is that sampling error is the real explanation for the association that we are observing w Tests of significance n a figure from 0. 000 to 1. 000 l the probability of error

P - value w P = 0. 04 n in only 4 out of every 100 samples would we expect to see the association we have noted purely by chance. l The much stronger likelihood is that the association is real

Statistical significance w Every finding derived from a sample is associated with some probability of error w How much probability of error should be tolerated? n n n Researcher decides sometimes referred to as tolerance limits 0. 05 common

Presenting data Correlation between wealth (acres and cows owned) and reproductive success (number of wives and surviving offspring Reproductive success Wealth **p < 0. 01; *** p < 0. 001

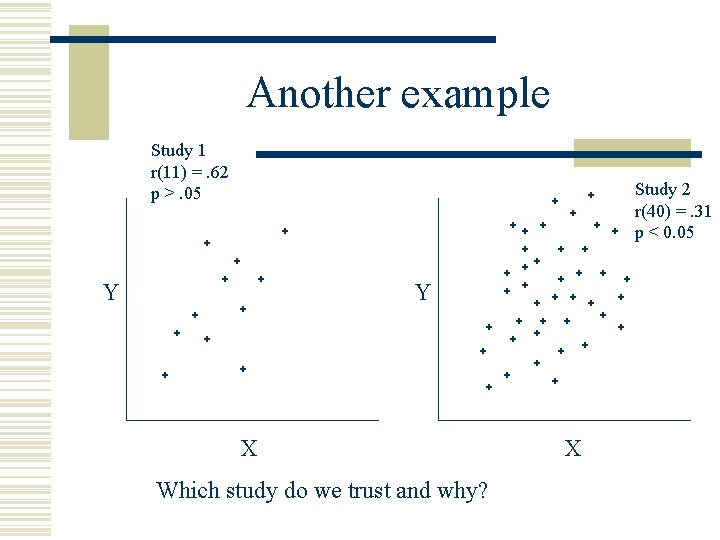
Another example Study 1 r(11) =. 62 p >. 05 Study 2 r(40) =. 31 p < 0. 05 Y Y X Which study do we trust and why? X

Means and proportions w Two means n T-test w Several means n Analysis of variance (ANOVA) w Proportions n Chi-square

Conclusion n Univariate analysis l Describing frequency distributions w shape; central tendency; dispersion l Inferential statistic w Interval estimates n Bivariate analysis w cross tabulation; correlation (strength, direction, nature) w scattergram; regression (prediction) w statistical significance w comparison of means (T; ANOVA) and proportions Chi-square