Summary Three Coordinates Tool Velocity Reference Frame Acceleration

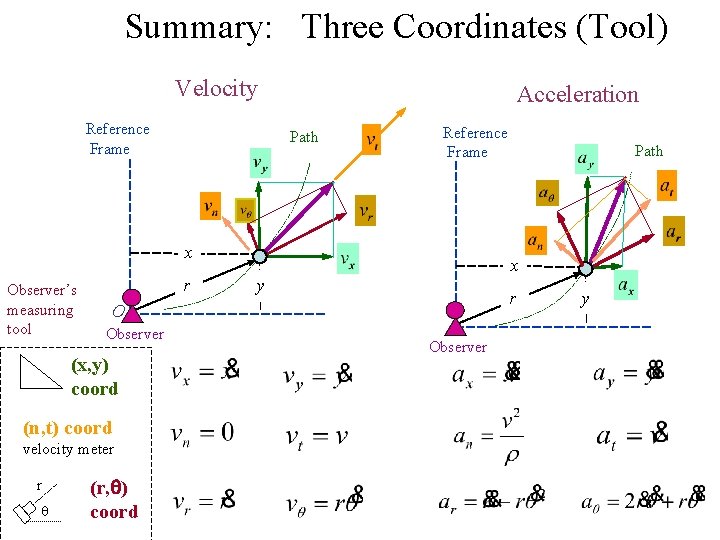
Summary: Three Coordinates (Tool) Velocity Reference Frame Acceleration Path Reference Frame x Observer’s measuring tool r x y r O Observer (x, y) coord Path y Observer (n, t) coord velocity meter r (r, q) coord 1

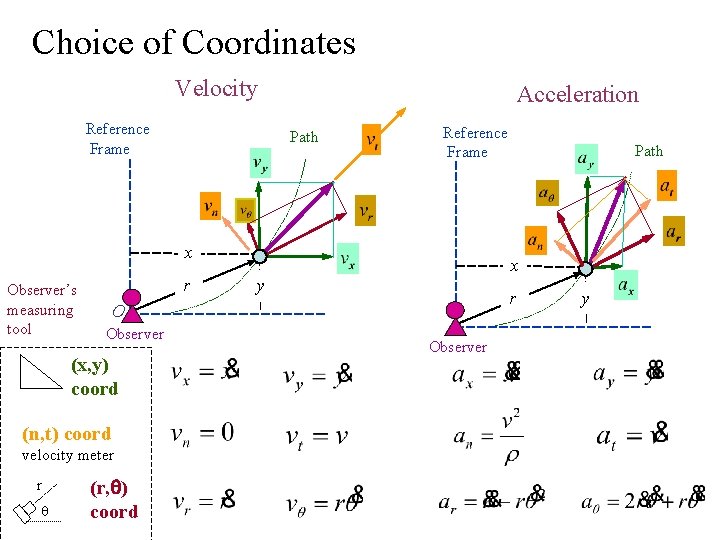
Choice of Coordinates Velocity Reference Frame Acceleration Path Reference Frame x Observer’s measuring tool r x y r O Observer (x, y) coord Path y Observer (n, t) coord velocity meter r (r, q) coord 2

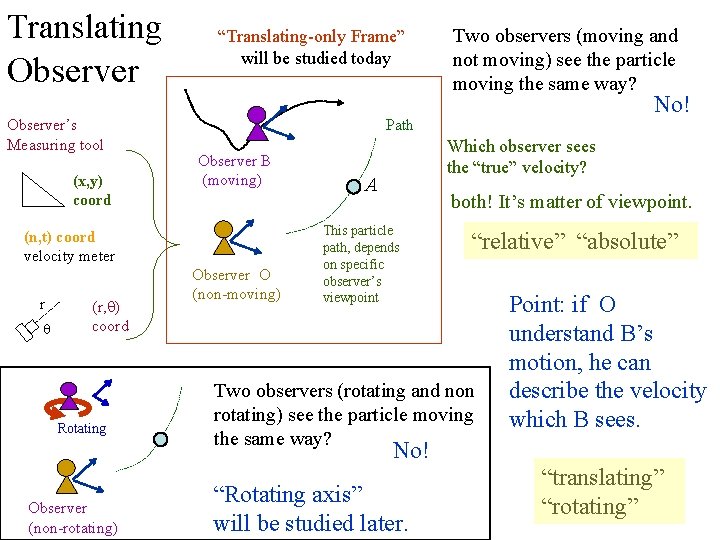
Translating Observer’s Measuring tool (x, y) coord “Translating-only Frame” will be studied today (r, ) coord Rotating No! Path Observer B (moving) (n, t) coord velocity meter r Two observers (moving and not moving) see the particle moving the same way? Observer O (non-moving) Which observer sees the “true” velocity? A both! It’s matter of viewpoint. This particle path, depends on specific observer’s viewpoint “relative” “absolute” Two observers (rotating and non rotating) see the particle moving the same way? Point: if O understand B’s motion, he can describe the velocity which B sees. No! Observer (non-rotating) “Rotating axis” will be studied later. “translating” “rotating” 4

2/8 Relative Motion (Translating axises) q Sometimes it is convenient to describe motions of a particle “relative” to a moving “reference frame” (reference observer B) q If motions of the reference axis is known, then “absolute motion” of the particle can also be found. Ø A = a particle to be studied Reference frame O Reference frame B A B O frame work O is considered as fixed (non-moving) Ø B = a “(moving) observer” § Motions of A measured by the observer at B is called the “relative motions of A with respect to B” § Motions of A measured using framework O is called the “absolute motions” § For most engineering problems, O attached to the earth surface may be assumed “fixed”; 5 i. e. non-moving.

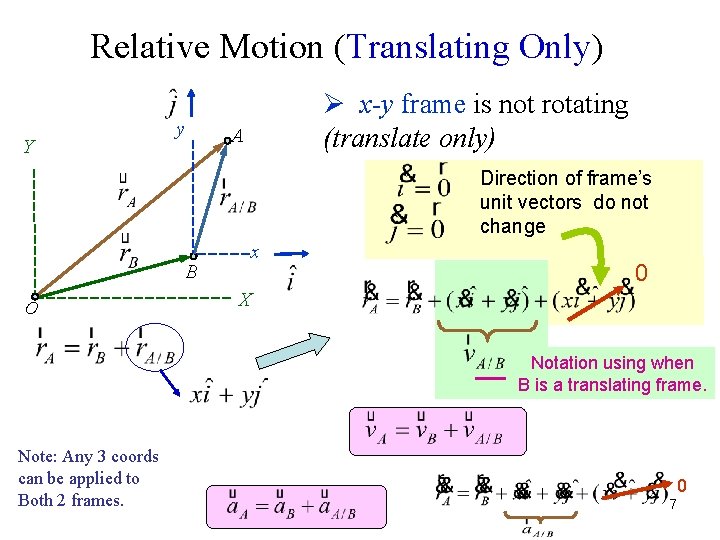
Relative position Y ØIf the observer at B use the x-y ** coordinate system to describe the position vector of A we have y A B O x ØHere we will consider only the case where the x-y axis is not rotating (translate only) X where = position vector of A relative to B (or with respect to B), and are the unit vectors along x and y axes (x, y) is the coordinate of A measured in x-y frame ** other coordinates systems can be used; e. g. n-t. 6

Relative Motion (Translating Only) Y y Ø x-y frame is not rotating (translate only) A Direction of frame’s unit vectors do not change B O x 0 X Notation using when B is a translating frame. Note: Any 3 coords can be applied to Both 2 frames. 0 7

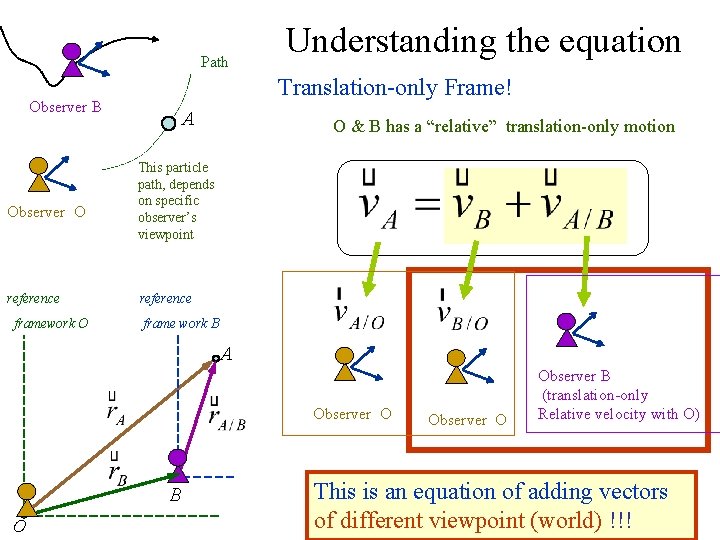
Path Translation-only Frame! Observer B Observer O reference framework O Understanding the equation A O & B has a “relative” translation-only motion This particle path, depends on specific observer’s viewpoint reference frame work B A Observer O B O Observer B (translation-only Relative velocity with O) This is an equation of adding vectors 8 of different viewpoint (world) !!!

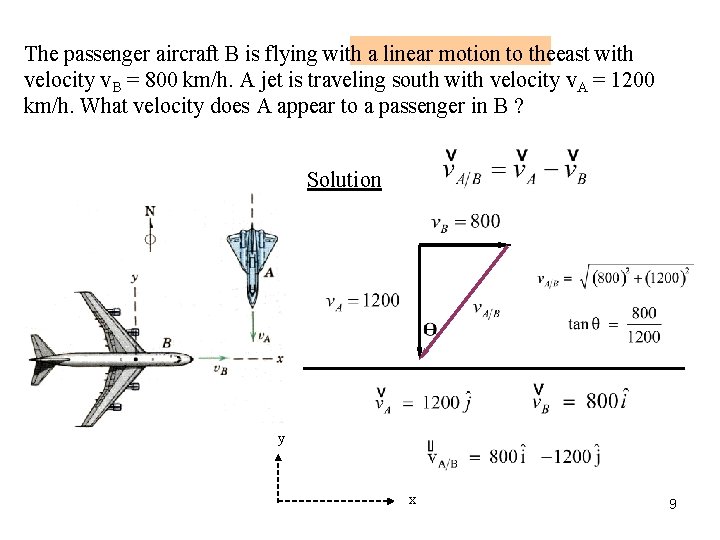
The passenger aircraft B is flying with a linear motion to theeast with velocity v. B = 800 km/h. A jet is traveling south with velocity v. A = 1200 km/h. What velocity does A appear to a passenger in B ? Solution y x 9

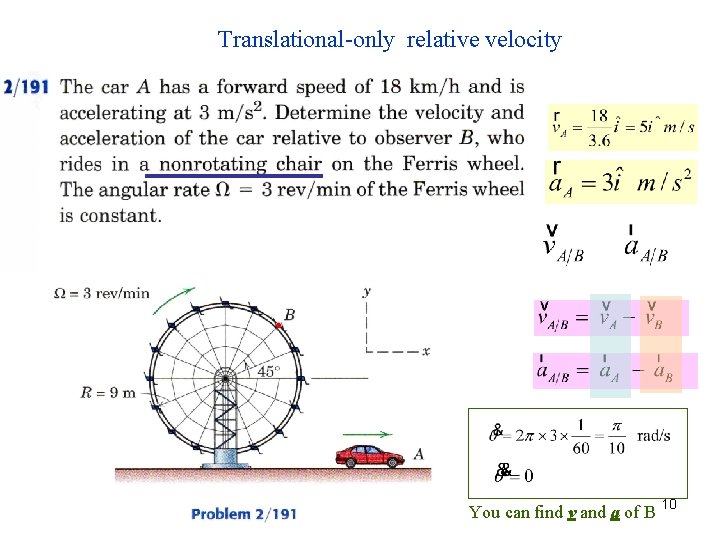
Translational-only relative velocity You can find v and a of B 10

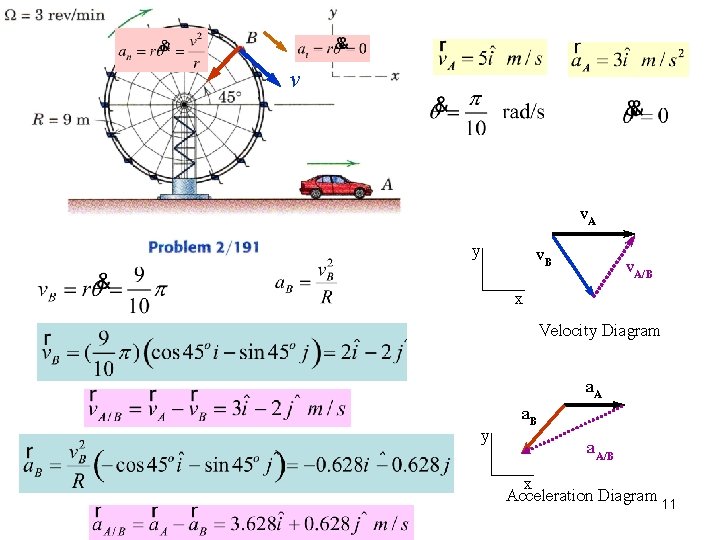
v v. A y v. B x y a. B v. A/B Velocity Diagram a. A/B x Acceleration Diagram 11

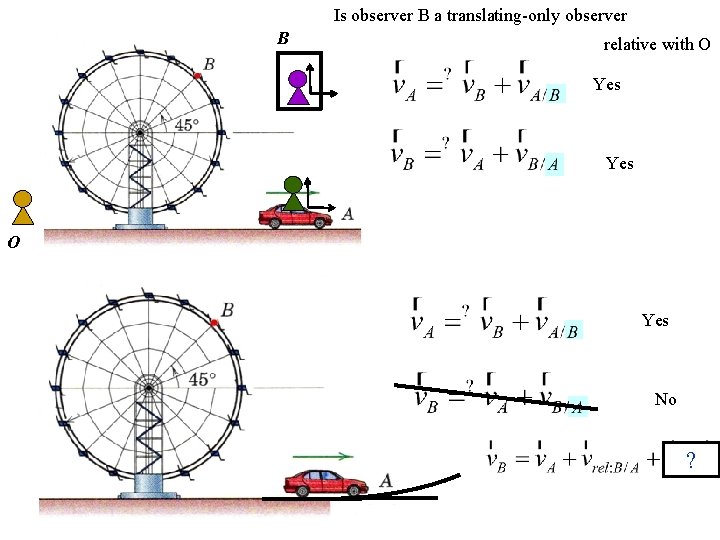
Is observer B a translating-only observer B relative with O Yes No ?

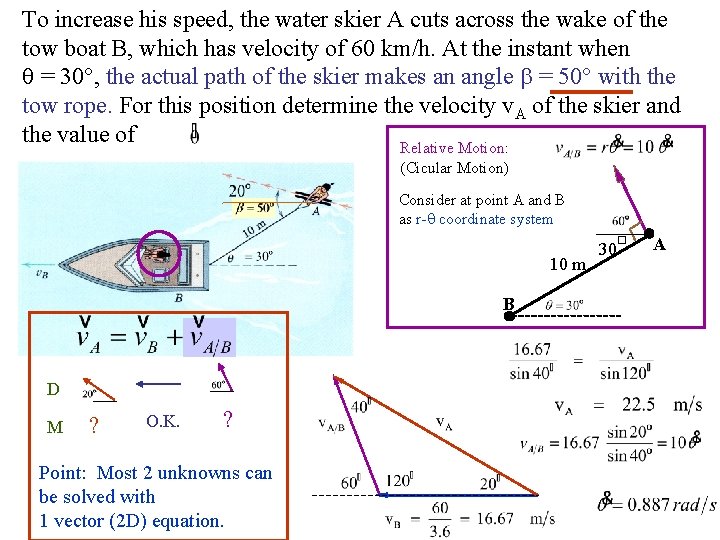
To increase his speed, the water skier A cuts across the wake of the tow boat B, which has velocity of 60 km/h. At the instant when = 30°, the actual path of the skier makes an angle = 50° with the tow rope. For this position determine the velocity v. A of the skier and the value of Relative Motion: (Cicular Motion) Consider at point A and B as r- coordinate system 10 m 30 o A B D M ? O. K. ? Point: Most 2 unknowns can be solved with 1 vector (2 D) equation. 13

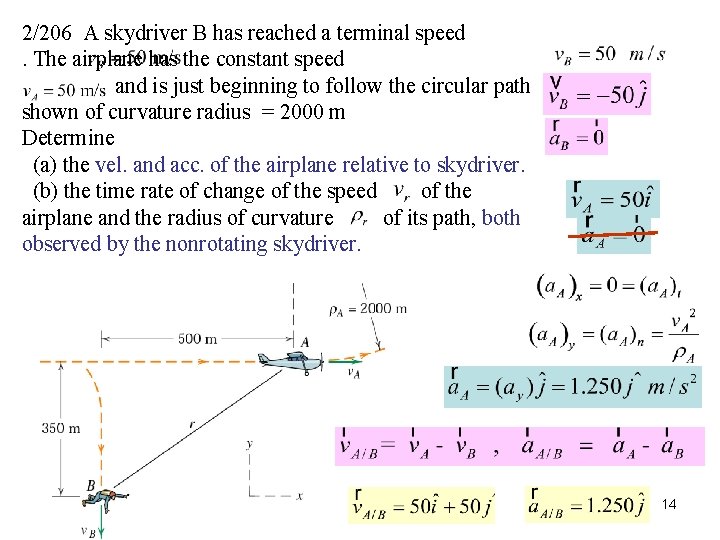
2/206 A skydriver B has reached a terminal speed. The airplane has the constant speed and is just beginning to follow the circular path shown of curvature radius = 2000 m Determine (a) the vel. and acc. of the airplane relative to skydriver. (b) the time rate of change of the speed of the airplane and the radius of curvature of its path, both observed by the nonrotating skydriver. 14

(b) the time rate of change of the speed of the airplane and the radius of curvature of its path, both observed by the nonrotating skydriver. t n 15

16

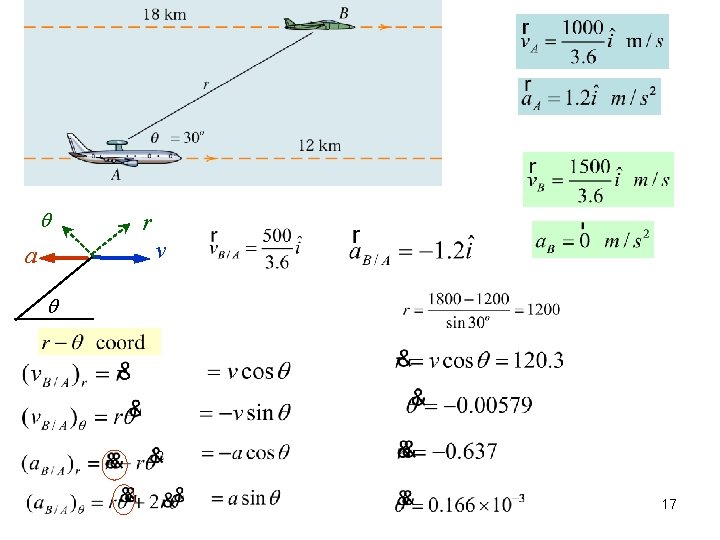
r v a 17