Summary Statistics Mean Median Standard Deviation and More

Summary Statistics: Mean, Median, Standard Deviation, and More “Seek simplicity and then distrust it. ” (Dr. Monticino)

Assignment Sheet n n Read Chapter 4 Homework #3: Due Wednesday Feb. 9 th Ù Chapter 4 · · n n n exercise set A: exercise set C: exercise set D: exercise set E: 1 -6, 8, 9 1, 2, 3 1 - 4, 8, 4, 5, 7, 8, 11, 12 Quiz #2 will be over Chapter 2 Quiz #3 on basic summary statistic calculations – mean, median, standard deviation, IQR, SD units If you’d like a copy of notes - email me

Overview n Measures of central tendency Mean (average) Ù Median Ù Outliers Ù n Measures of dispersion Ù Standard deviation · Standard deviation units Range Ù IQR Ù n Review and applications

Central Tendency n Measures of central tendency - mean and median - are useful in obtaining a single number summary of a data set Mean is the arithmetic average Ù Median is a value such that at least 50% of the data is less and at least 50% is greater Ù

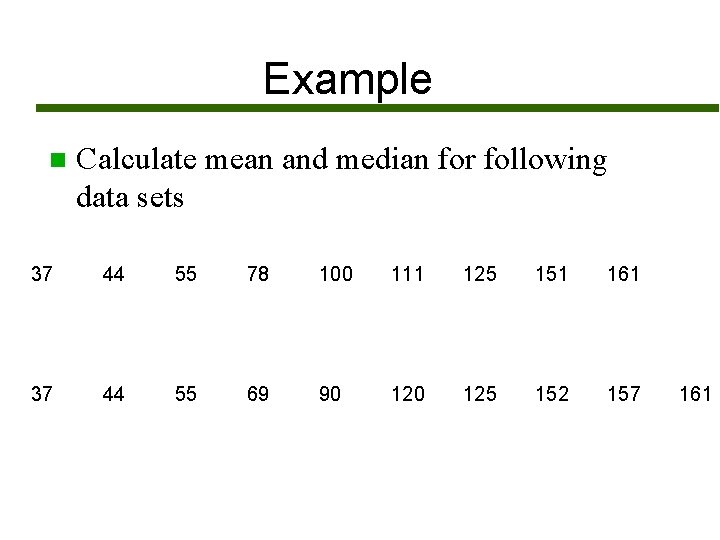
Example n Calculate mean and median for following data sets 37 44 55 78 100 111 125 151 161 37 44 55 69 90 125 152 157 161

Outliers and Robustness n Mean can be sensitive to outliers in data set Ù Not robust to data collection errors or a single unusual measurement Ù Blind calculation can give misleading results mean = 170. 35 median = 151

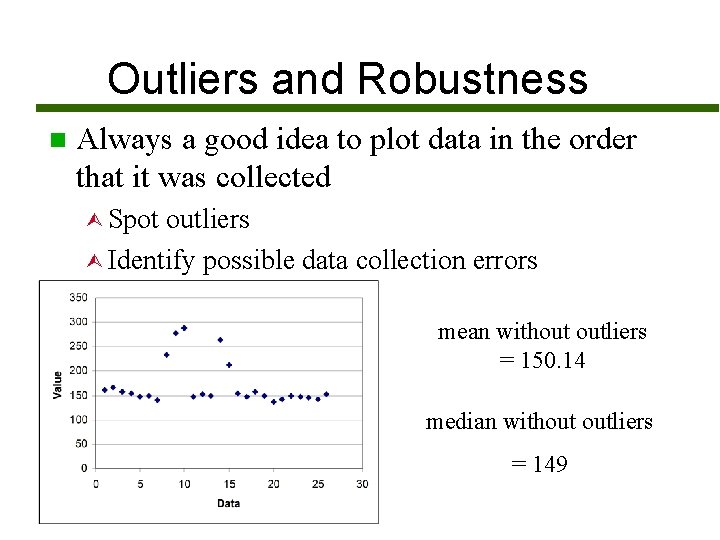
Outliers and Robustness n Always a good idea to plot data in the order that it was collected Ù Spot outliers Ù Identify possible data collection errors mean without outliers = 150. 14 median without outliers = 149

Outliers and Robustness n Median can be a more robust measure of central tendency than mean Ù Life expectancy · U. S. males: mean = 80. 1, median = 83 · U. S. females: mean = 84. 3, median = 87 Ù Household income · Mean = $51, 855, median = $38, 885 ·. 3% account for 12% of income Ù Net worth · Mean = $282, 500, median = $71, 600

Which Central Tendency Measure? n n n Calculate mean, median and mode Plot data Create histogram to inspect mode(s) Do not delete data points Ù If analyze data without outliers, report and explain outliers Many statistical studies involve studying the difference between population means Ù Reporting the mean may be dictated by objective of study

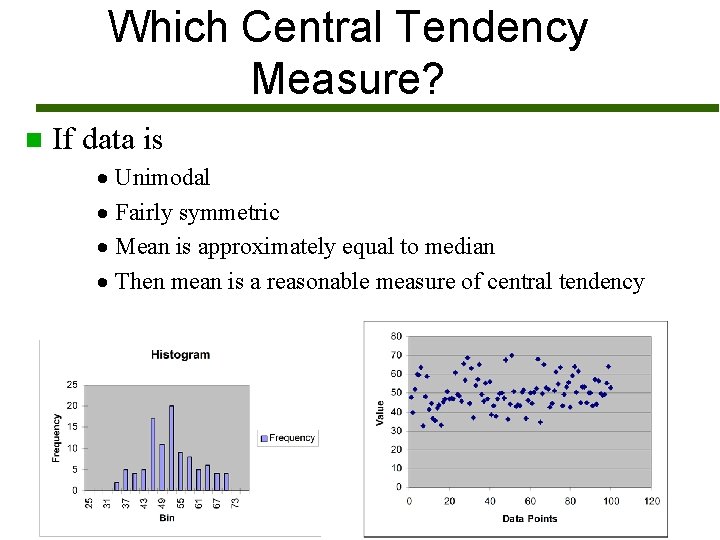
Which Central Tendency Measure? n If data is · Unimodal · Fairly symmetric · Mean is approximately equal to median · Then mean is a reasonable measure of central tendency

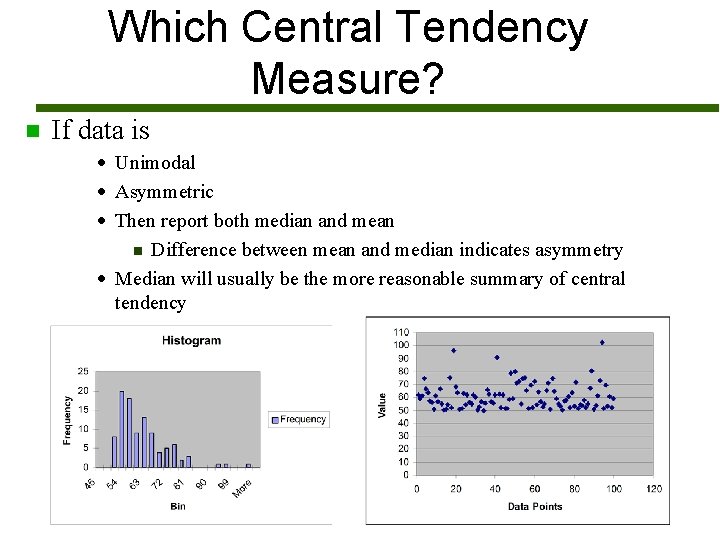
Which Central Tendency Measure? n If data is · Unimodal · Asymmetric · Then report both median and mean n Difference between mean and median indicates asymmetry · Median will usually be the more reasonable summary of central tendency

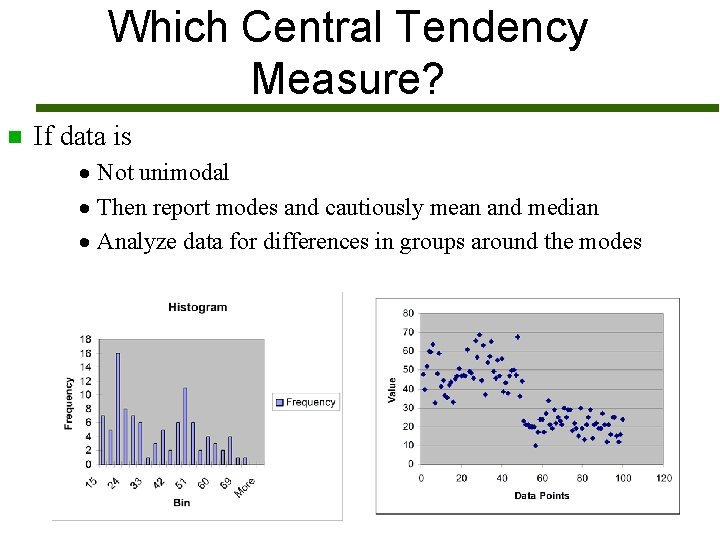
Which Central Tendency Measure? n If data is · Not unimodal · Then report modes and cautiously mean and median · Analyze data for differences in groups around the modes

Limitations of Central Tendency n Any single number summary may not adequately represent data and may hide differences between data sets Ù Example

Measures of Dispersion n Including an additional statistic - a measure of dispersion - can help distinguish between data sets which have similar central tendencies Range: max - min Ù Standard deviation: root mean square difference from the mean Ù

Measures of Dispersion n Examples Ù Range

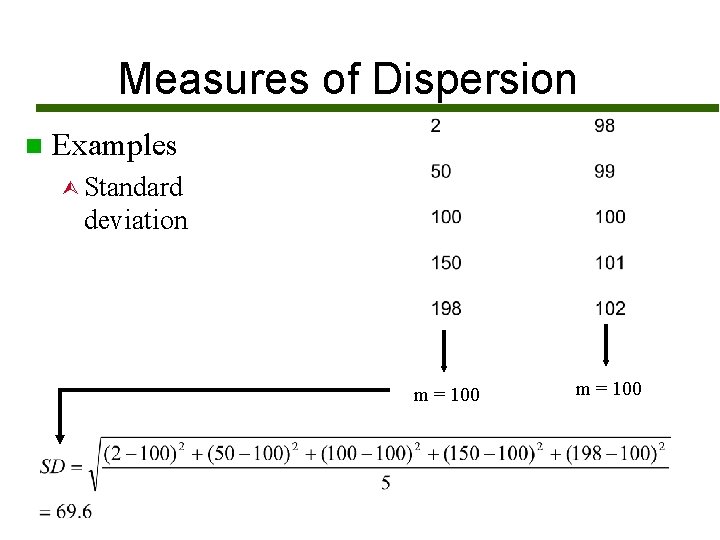
Measures of Dispersion n Examples Ù Standard deviation m = 100

Measures of Dispersion n Both range and standard deviation can be sensitive to outliers However, many data sets can be characterized by mean and SD Ù If the values of the data set are distributed in an approximately bell shape, the Ù · ~68% of the data will be within 1 SD unit of mean, ~95% will be within 2 SD units and nearly all will be within 3 SD units

Measures of Dispersion n Example Suppose data set has mean = 35 and SD = 7 Ù How many SD units away from the mean is 42? Ù How many SD units away from the mean is 38? Ù How many SD units away from the mean is 30? Ù Ù Assuming bell shape distribution, ~95% are between what two values?

Measures of Dispersion n A robust measure of dispersion is the interquartile range Q 1: value such that 25% of data less than, and 75% greater than Ù Q 3: value such that 75% less than, and 25% greater than Ù IQR = Q 3 - Q 1 Ù

Example n Calculate range, standard deviation and interquartile range for the following data sets 1 98 99 100 100 102 104 107 95 98 99 100 100 102 104 107

Assignment, Discussion, Evaluation n n Read Chapter 4 Discussion problems Ù Chapter 4 · · n exercise set A: exercise set C: exercise set D: exercise set E: 1 -6, 8, 9 1, 2, 3 1 - 4, 8, 4, 5, 7, 8, 11, 12 Quiz #3 on basic summary statistic calculations – mean, median, standard deviation, IQR, SD units

Review of Definitions n Measures of central tendency Ù Mean (average): Ù Median · If odd number of data points, “middle” value · If even number of data points, average of two “middle” values

Question and Examples n Can mean be larger than median? Can median be larger than mean? Ù n n Give examples Can mean be a negative number? Can the median? The average height of three men is 69 inches. Two other men enter the room of heights 73 and 70 inches. What is the average height of all five men?

Questions and Examples n The average of a data set is 30. A value of 8 is added to each element in the data set. What is the new average? Ù Each element of the data set is increased by 5%. What is the new average? Ù n Suppose that data consists of only 1’s and 0’s Ù What does the average represent? · Application: an experiment is performed and only two outcomes can occur · Label one type of outcome 1 and the other 0 n For the data set 31, 45, 72, 86, 62, 78, 50, find the median, Q 1 (25 th percentile) and Q 3 (75 th percentile)

Review of Definitions n Measures of dispersion Ù Standard Ù Range deviation = = max - min Ù IQR = Q 3 - Q 1

Questions and Examples n n Can the SD be negative? Can the range? Can the IQR? Can the SD equal 0? For the data set 3, 1, 5, 2, 1, 6 find the SD, range and IQR The average weight for U. S. men is 175 lbs and the standard deviation is 20 lbs If a man weighs 190 lbs. , how many standard deviation units away from the mean weight is he? Ù Assuming a normal (bell-shaped) distribution for weight, ninety-five percent of U. S. men weigh between what two values? Ù

Questions and Examples n The average of a data set is 23 and the standard deviation is 5 ÙA value of 8 is added to each element in the data set. What is the new standard deviation? Ù Each element of the data set is increased by 5%. What is the new standard deviation? (Dr. Monticino)