Summary Simple runtime problems Counting instructions Detailed Terminology

Summary • Simple runtime problems • ‘Counting’ instructions – Detailed • Terminology and notation: – log 2 N = lg N 1

Estimate runtime • Problem: The total number of instructions in a program (or a piece of code) is 1012 and it runs on a computer that executes 109 instructions per second. How long will it take to run this program? Give the answer in seconds. If it is very large, transform it in larger units (hours, days, years). • Summary: – Total instructions: 1012 – Speed: 109 instructions/second • Answer: – Time = (total instructions)/speed = (1012 instructions) / (109 instr/sec) = 103 seconds ~ 15 minutes • Note that this computation is similar to computing the time it takes to travel a certain distance ( e. g. 120 miles) given the speed (e. g. 60 miles/hour). 2

Estimate runtime • A slightly different way to formulate the same problem: – total number of instructions in a program (or a piece of code) is 1012 and – it runs on a computer that executes one instruction in one nanosecond (10 -9 seconds) – How long will it take to run this program? Give the answer in seconds. If it is very large, transform it in larger units (hours, days, years) • Summary: – 1012 total instructions – 10 -9 seconds per instruction • Answer: – Time = (total instructions) * (seconds per instruction) = (1012 instructions)* (10 -9 sec/instr) = 103 seconds ~ 15 minutes 3

C conventions • Body of loops : – Several instructions with curly braces – One instruction indented (with or without curly braces) – No instruction • With semicolon, or without 4

Counting instructions: detailed Worksheet Count in detail the total number of instructions executed by each of the following pieces of code: // Example A. Notice the ; at the end of the for loop. temp = 5; x = temp * 2; for (i = 0; i<n; i++) ; -----------------------------------------------// Example B (source: Dr. Bob Weems) for (i=0; i<n; i++) for (t=0; t<p; t++) { c[i][t]=0; for (k=0; k<r; k++) c[i][t]+=a[i][k]*b[k][t]; } ----------------------------------------------- 5

Counting instructions: detailed Answers 1 + n* (1 + body_instr_count) false true for (init; cond; update) // assume the condition is TRUE n times body // Example A. Notice the ; at the end of the for loop. temp = 5; x = temp * 2; for (i = 0; i<n; i++) ; 2 + 1 + n* (1 + 0) = 4 + 2 n -----------------------------------------------// Example B (source: Dr. Bob Weems) for (i=0; i<n; i++) 1 + n * (1 + ___ ) = 2 + n * (2 + 5*p + 3*p*r) = 2 + 4*n + 5*n*p + 3*n*p*r for (t=0; t<p; t++) 1 + p* (1 + 1 + ____) = 2 + p * (3 + 2 + 3*r) = 2 + 5*p + 3*p*r { c[i][t]=0; 1 + r* (1 + 1) = 2 + 3 * r for (k=0; k<r; k++) c[i][t]+=a[i][k]*b[k][t]; 6 }

Counting instructions: sequential vs nested loops Worksheet // Example sequential vs nested for (t=0; t<n; t++) printf("A"); for (i=0; i<p; i++) { for (k=0; k<r; k++) printf("B"); } 7

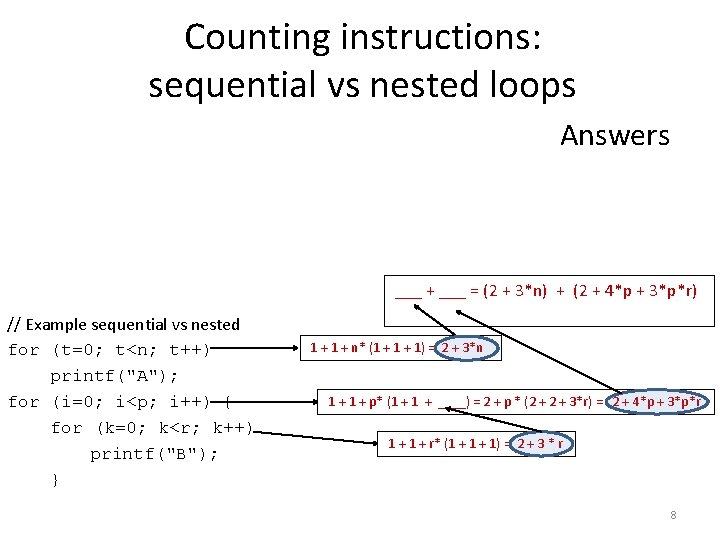
Counting instructions: sequential vs nested loops Answers ___ + ___ = (2 + 3*n) + (2 + 4*p + 3*p*r) // Example sequential vs nested for (t=0; t<n; t++) printf("A"); for (i=0; i<p; i++) { for (k=0; k<r; k++) printf("B"); } 1 + n* (1 + 1) = 2 + 3*n 1 + p* (1 + ____) = 2 + p * (2 + 3*r) = 2 + 4*p + 3*p*r 1 + r* (1 + 1) = 2 + 3 * r 8

CLRS • The textbook, CLRS, provides a more detailed analysis that uses different costs (time) for instructions (based on their type). – Easy to adapt the above method to do that: just reapply the method, but count only specific instructions (assignments, additions, comparisons, …) – More details that we will want to skip over in the end (=> use Big-Oh). 9

Detailed instruction count Worksheet • What does this code do? • Give a detailed count of instructions for the case when the while loop stops because the condition (left <= right) is false. /* code adapted from Sedgewick Assume A is sorted in increasing order and that left and right are in range indexes for A. */ 1. int mistery(int A[], int v, int left, int right){ 3. while (left <= right) { 4. int m = (left+right)/2; 5. if (v == A[m]) return m; 6. if (v < A[m]) 7. right = m-1; 8. else 9. left = m+1; 10. } 11. return -1; 12. } 10