Summary Lecture 12 Rotational Motion 10 8 Torque

Summary Lecture 12 Rotational Motion 10. 8 Torque 10. 9 Newton 2 for rotation 10. 10 Work and Power 11. 2 Rolling motion Today 20 -minute test on material in lectures 1 -7 at end of lecture Problems: Chap. 10: 21, 28 , 33, 39, 49, 54, 67

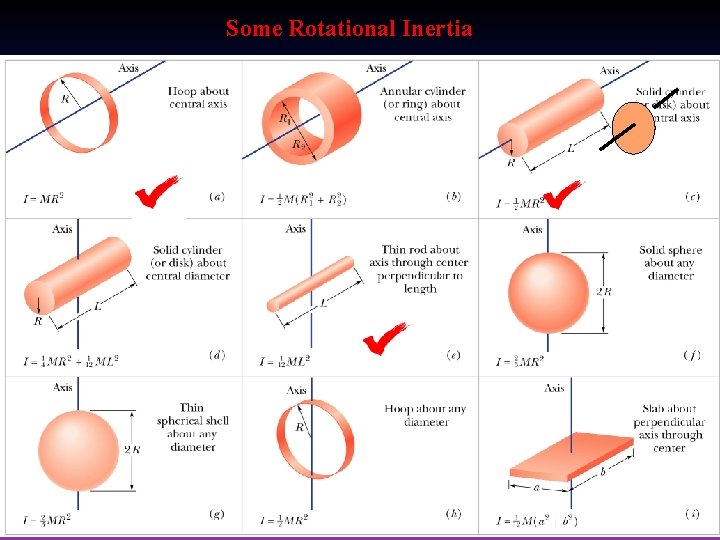
Some Rotational Inertia

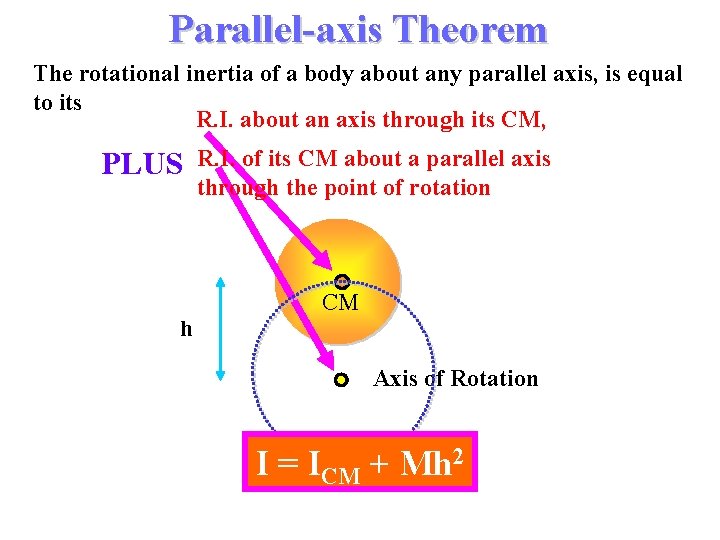
Parallel-axis Theorem The rotational inertia of a body about any parallel axis, is equal to its R. I. about an axis through its CM, PLUS R. I. of its CM about a parallel axis through the point of rotation CM h Axis of Rotation I = ICM + Mh 2

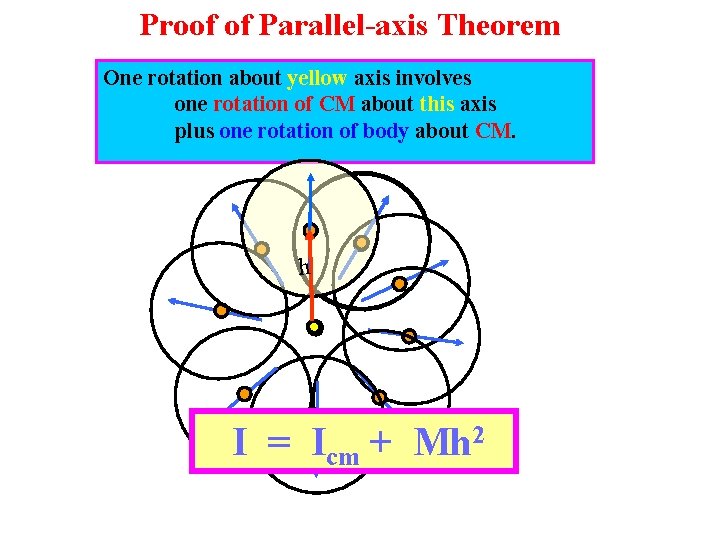
Proof of Parallel-axis Theorem One rotation about yellow axis involves one rotation of CM about this axis plus one rotation of body about CM. h I = Icm + Mh 2

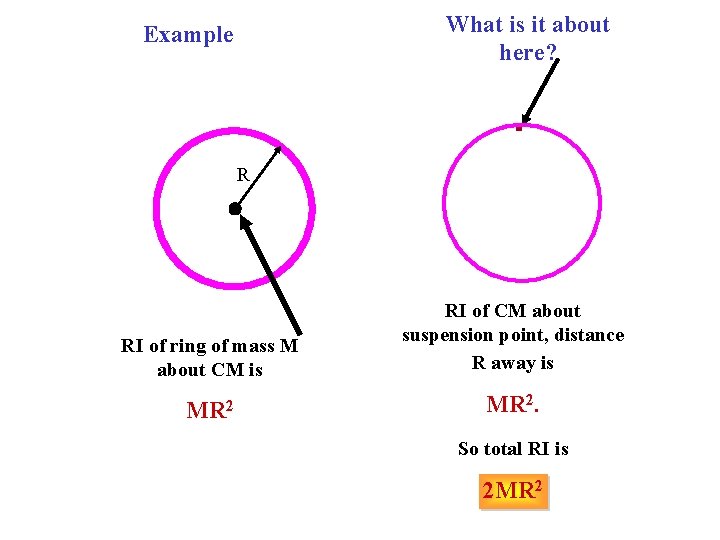
What is it about here? Example R RI of ring of mass M about CM is RI of CM about suspension point, distance R away is MR 2. So total RI is 2 MR 2

The Story so far. . . Rotational Variables , , relation to linear variables vector nature Rotational kinematics with const. Analogue equations to linear motion Rotation and Kinetic Energy Rotational Inertia

Torque …is the “turning ability” of a force Where would you put the door knob? here? r The magnitude of the torque is Fr, and this is greater here! or here? r F F

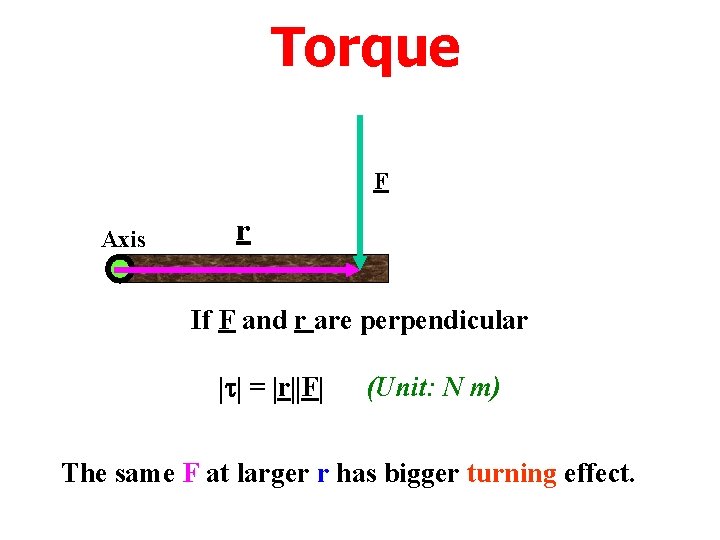
Torque F Axis r If F and r are perpendicular = r F (Unit: N m) The same F at larger r has bigger turning effect.

In General Torque is a vector F Axis r Fsin =rx. F = r F sin = r x perp component of F Direction of : Perpendicular to r and F Sense: Right-hand screw rule (out of screen) (Hint: Which way would it accelerate the body? Sense is same as change in ang vel. . )

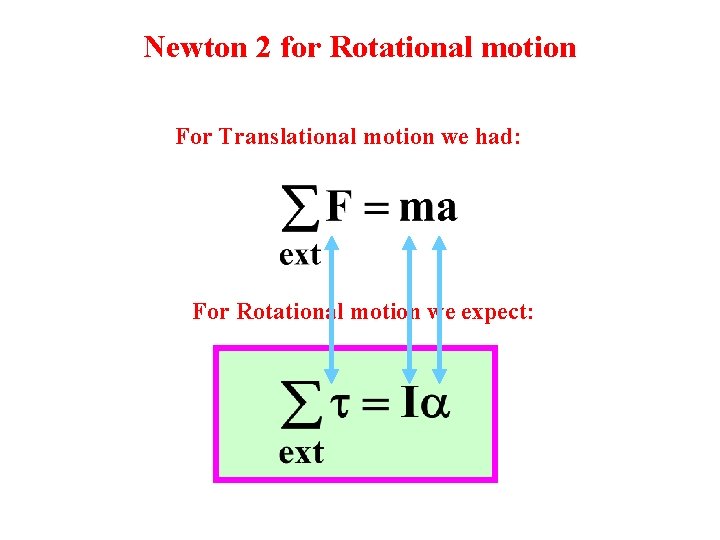
Newton 2 for Rotational motion For Translational motion we had: For Rotational motion we expect:

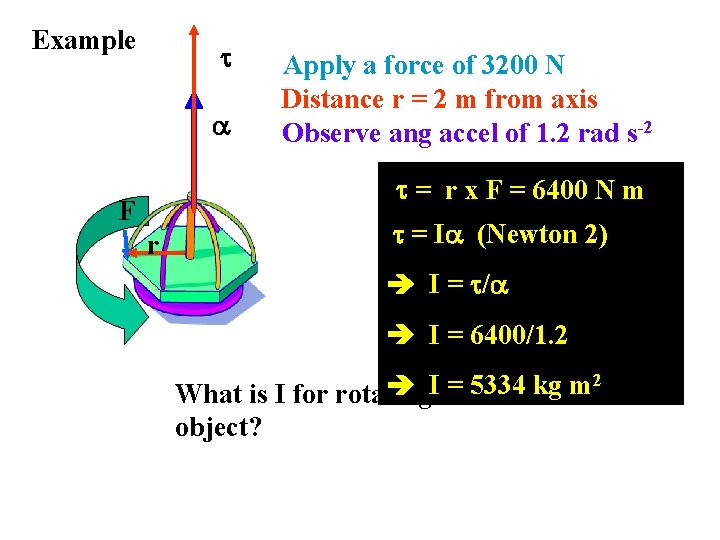
Example Apply a force of 3200 N Distance r = 2 m from axis Observe ang accel of 1. 2 rad s-2 = r x F = 6400 N m F r = I (Newton 2) I = / I = 6400/1. 2 2 I = 5334 kg m What is I for rotating object?

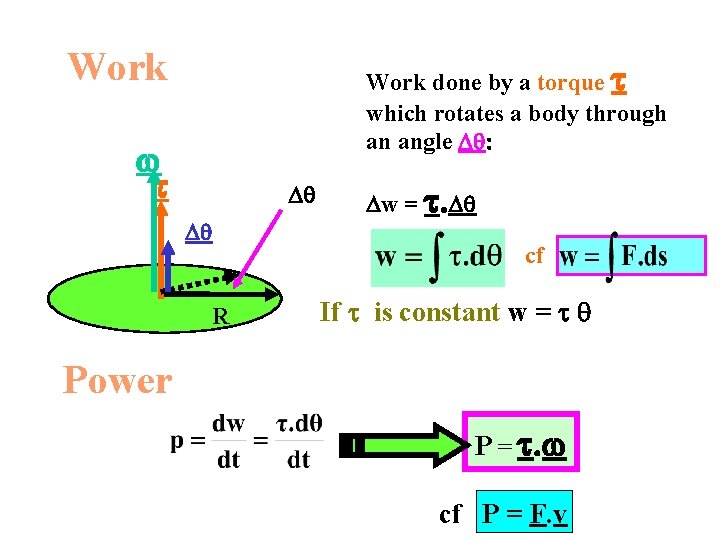
Work done by a torque which rotates a body through an angle D : D D R Dw = . D cf If is constant w = Power P = . cf P = F. v

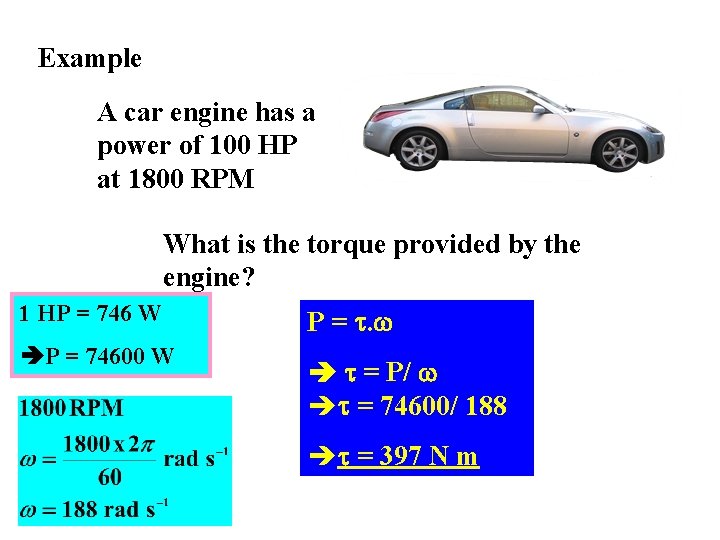
Example A car engine has a power of 100 HP at 1800 RPM What is the torque provided by the engine? 1 HP = 746 W P = 74600 W = P/ è = 74600/ 188 è = 397 N m

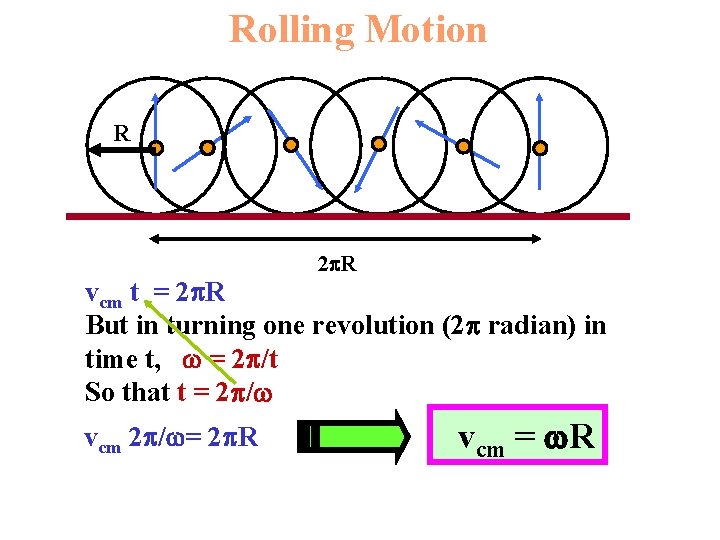
Rolling Motion R 2 R vcm t = 2 R But in turning one revolution (2 radian) in time t, = 2 /t So that t = 2 / vcm 2 / = 2 R vcm = R

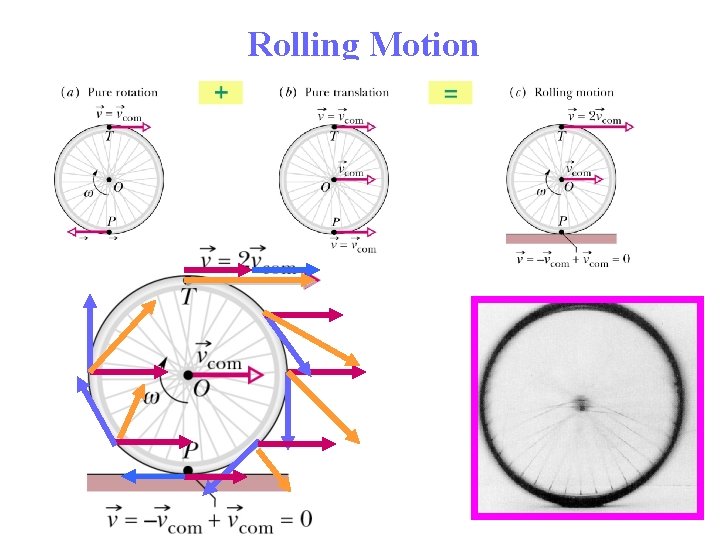
Rolling Motion

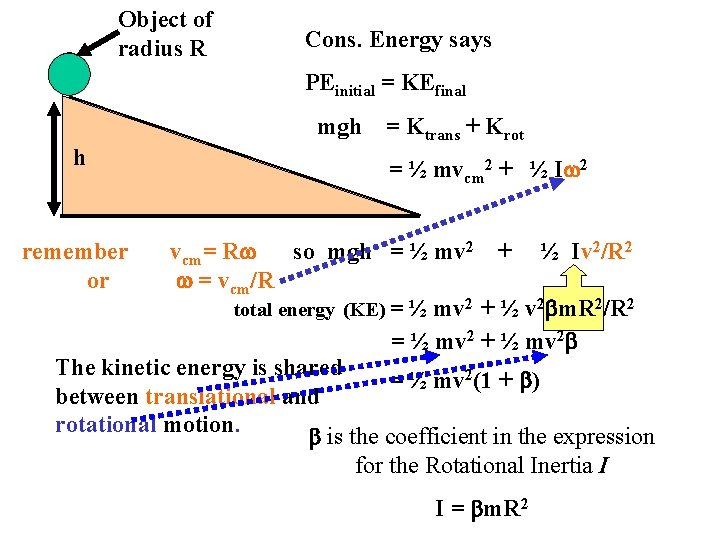
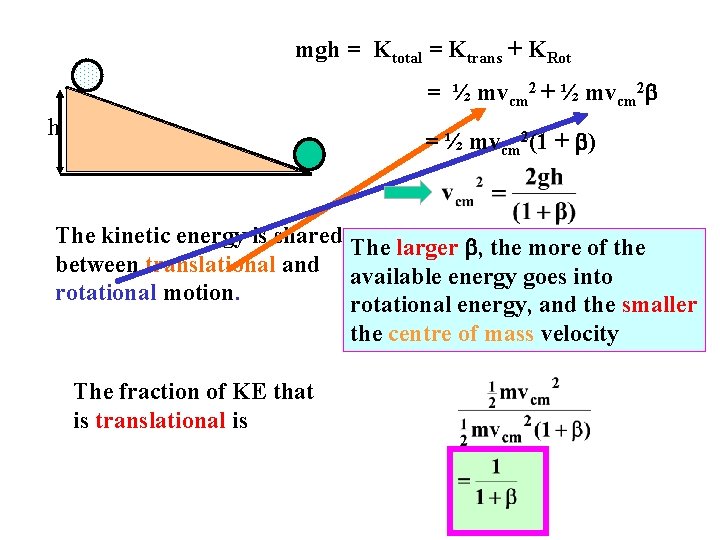
Object of radius R Cons. Energy says PEinitial = KEfinal mgh h = Ktrans + Krot = ½ mvcm 2 + ½ I 2 remember or vcm= R so mgh = ½ mv 2 + ½ Iv 2/R 2 = vcm/R total energy (KE) = ½ mv 2 + ½ v 2 bm. R 2/R 2 = ½ mv 2 + ½ mv 2 b The kinetic energy is shared = ½ mv 2(1 + b) between translational and rotational motion. b is the coefficient in the expression for the Rotational Inertia I I = bm. R 2

mgh = Ktotal = Ktrans + KRot = ½ mvcm 2 + ½ mvcm 2 b h h = ½ mvcm 2(1 + b) The kinetic energy is shared The larger b, the more of the between translational and available energy goes into rotational motion. rotational energy, and the smaller the centre of mass velocity The fraction of KE that is translational is