Summary for Lecture 3 4 5 Projectile motion

Summary for Lecture 3 4. 5 Projectile motion 4. 6 Range of projectile Dynamics 4. 8 Relative motion in 1 D 4. 9 Relative motion in 3 -D 4. 7 Circular motion (study at home) 5. 2 Newton 1 5. 3 -5. 5 Force, mass, and Newton 2 Problems Chap. 4 24, 45, 53,

First-year Learning Centre Tutors are available to help you from 12. 30 pm to 2. 30 pm on Tuesday – Friday In the First-year Learning Centre

Notices Representative for SSLC (Staff-Student Liaison Cttee) Physics Phrequent Phlyers Clarify the physics Extend your knowledge Ask the lecturer Room pp 211 Physics Podium Thursdays 12 – 2 pm

Parabola Running out of “impetus” 2 angles for any range Max range 45 o Gallileo

What do we know from experience? The trajectory depends on: Initial velocity Projection angle Anything else? Ignore for now Air resistance

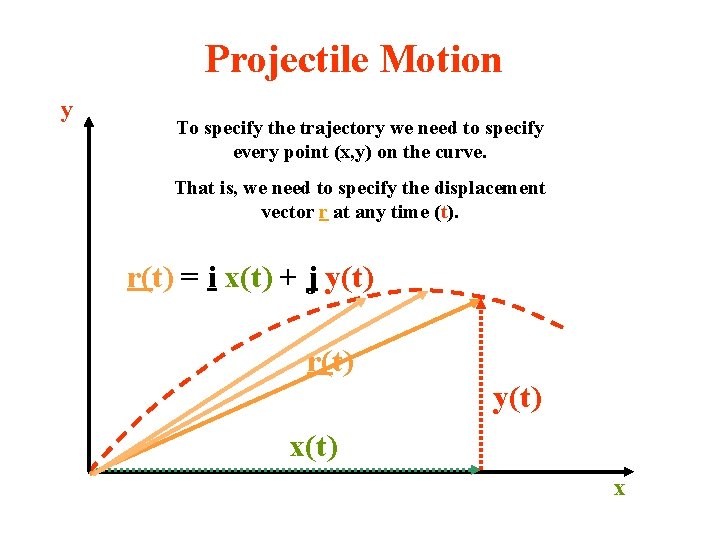
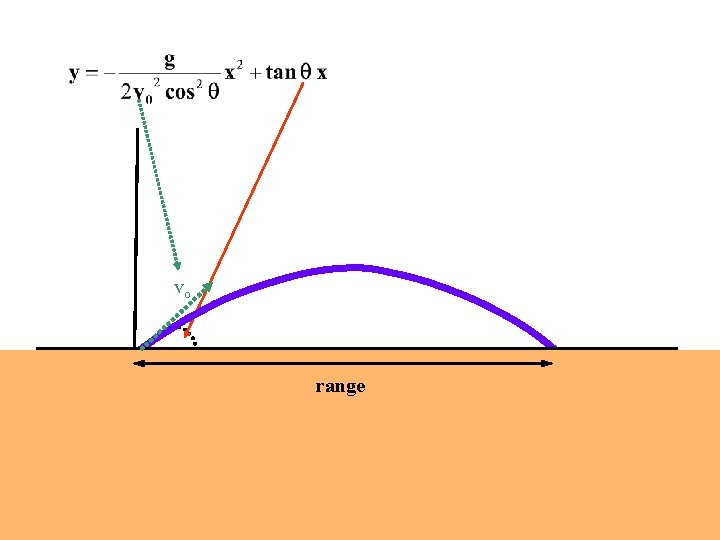
Projectile Motion y To specify the trajectory we need to specify every point (x, y) on the curve. That is, we need to specify the displacement vector r at any time (t). r(t) = i x(t) + j y(t) r(t) y(t) x

What do we know? -g y Usually we know the initial vector velocity vo. v 0 = ivox + j voy = vo v 0 cos v 0 sin i v 0 cos + jv 0 sin We know acceleration is constant = -g. accel is a vector a = iax + jay =i 0 -jg x

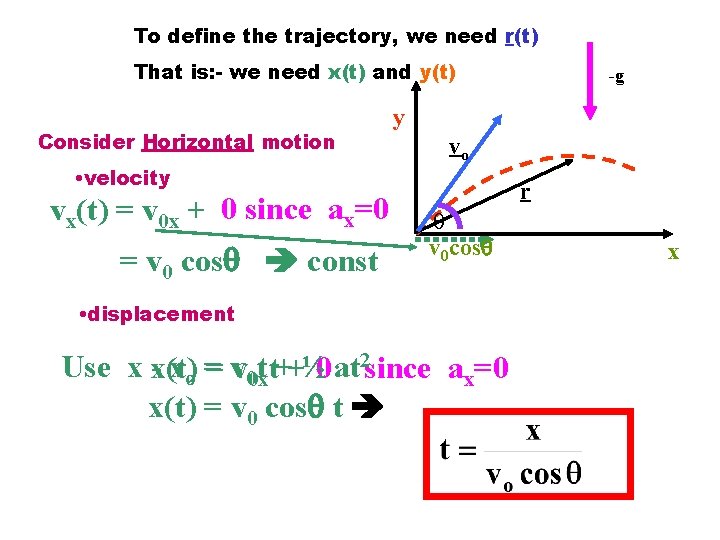
Finding an expression for Projectile motion The vertical component of the projectile motion is the same as for a falling object The horizontal component is motion at constant velocity

To define the trajectory, we need r(t) That is: - we need x(t) and y(t) Consider Horizontal motion • velocity vx(t) = v 0 x + a 0 xtsince ax=0 = v 0 cos const -g y vo r v 0 cos • displacement Use x x(t) - xo = v 00 xt t++½½a t 2 0 atx 2 since ax=0 x(t) = v 0 cos t x

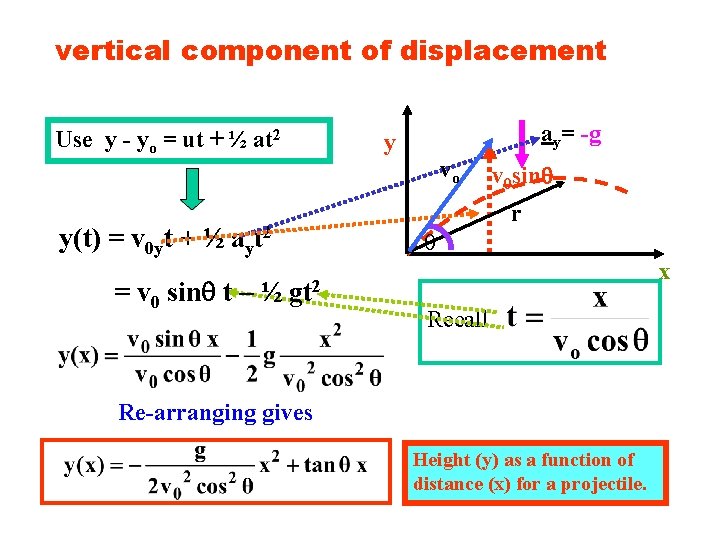
vertical component of displacement Use y - yo = ut + ½ at 2 y(t) = v 0 yt + ½ ayt 2 = v 0 sin t – ½ gt 2 ay= -g y vo v 0 sin r x Recall Re-arranging gives Height (y) as a function of distance (x) for a projectile.

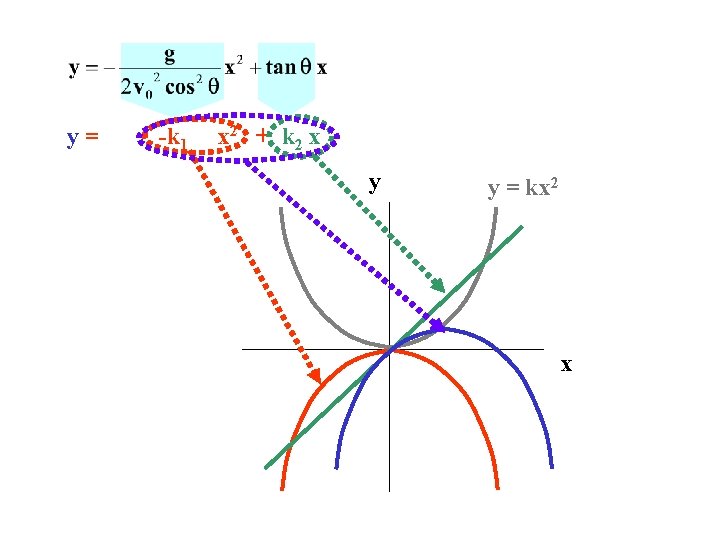
y= -k 1 x 2 + k 2 x y y = kx 2 x

y vo range x y = -k 1 x 2 + k 2 x

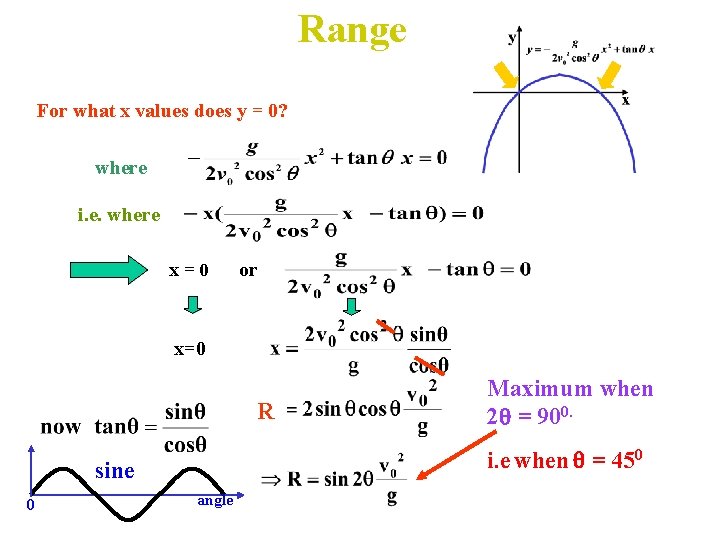
Range For what x values does y = 0? where i. e. where x=0 or x=0 R i. e when = 450 sine 0 Maximum when 2 = 900. angle

http: //www. colorado. edu/physics/phet/web-pages/simulations-base. html

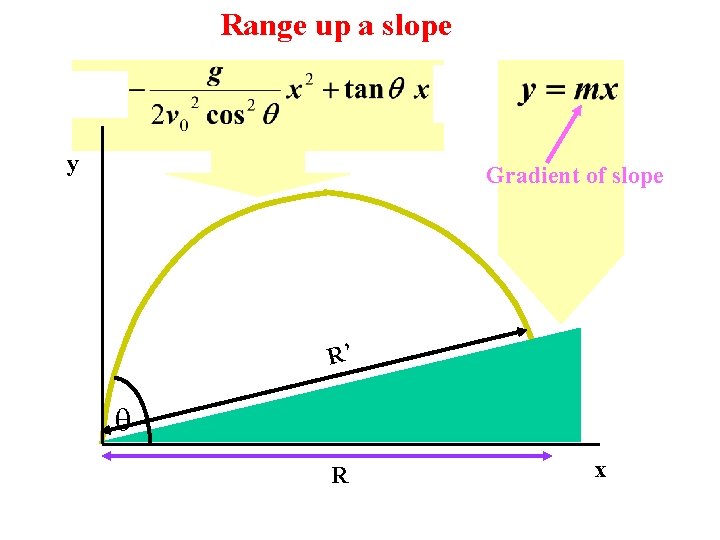
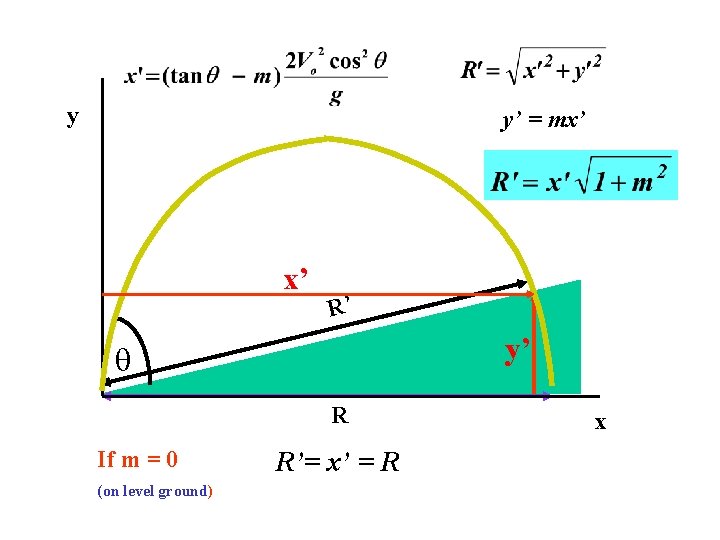
Range up a slope y Gradient of slope R’ R x

True for x = 0 or

y y’ = mx’ x’ R’ y’ R If m = 0 (on level ground) R’= x’ = R x

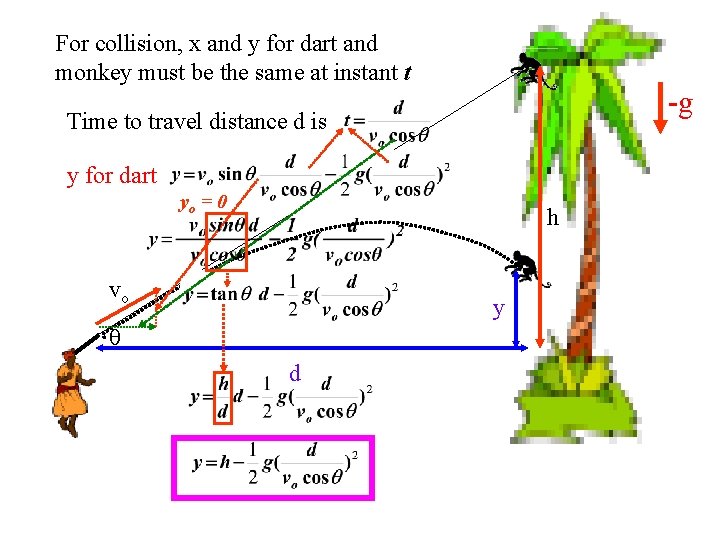
For collision, x and y for dart and monkey must be the same at instant t -g Time to travel distance d is y for dart y - y 0 = v 0 t + ½ at 2 yo = 0 h vo y d

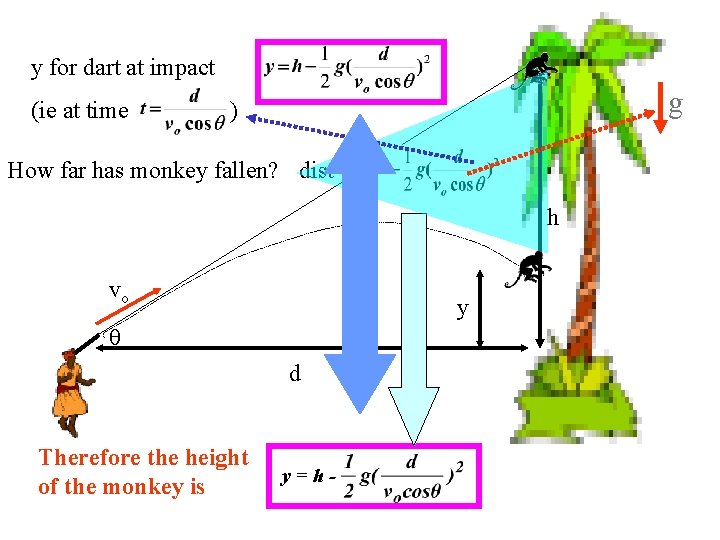
y for dart at impact (ie at time g ) How far has monkey fallen? dist = v 0 monkt + ½ at 2 h vo y d Therefore the height of the monkey is y=h-

Dynamics Kinematics HOW things move Dynamics WHY things move

P Q . 40% R

In the absence of a FORCE a body is at rest A body only moves if it is driven. 350 BC In the absence of a FORCE A body at rest REMAIN AT REST WILL If it is moving with a constant velocity, IT WILL CONTINUE TO DO SO 1660 AD

Dynamics Aristotle For an object to MOVE we need a force. Newton For an object to CHANGE its motion we need a force Newtons mechanics applies for motion in an inertial frame of reference! ? ? ? ?

Inertial Newton clarified the mechanics of e c n e r e f e r motion in the “real world”. frame He believed that there existed an absolute (not accelerating) l a i t r e n I reference frame, and an absolute time. Inertial e c n e r e f e r reference e His laws applied only when measurements were made in this frame reference frame…. . …or in any other reference frame that was at rest or moving at a constant velocity relative to this absolute frame. The laws of physics are always the same in any inertial reference frame.

Newton believed that there existed an absolute (not accelerating) reference frame, and an absolute time. Einstein recognised that all measurements of position and velocity (and time) are relative. There is no absolute reference frame. The laws of physics are always the same in any inertial reference frame.

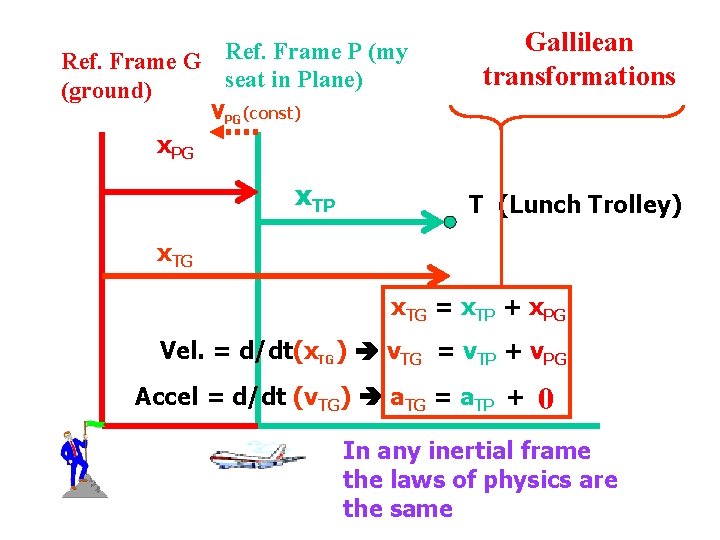
Frames of Reference In mechanics we need to specify position, velocity etc. of an object or event. y’ The reference frames may have a constant relative velocity We need to be able to relate one set of measurements to the other p z z’ This requires a frame of reference The reference frames for the same object may be different y o o x x’ The connection between inertial reference frames is the “Gallilean transformation”.

Ref. Frame G Ref. Frame P (my seat in Plane) (ground) Gallilean transformations VPG(const) x. PG x. TP T (Lunch Trolley) x. TG = x. TP + x. PG Vel. = d/dt(x. TG) v. TG = v. TP + v. PG Accel = d/dt (v. TG) a. TG = a. TP + a 0 PG In any inertial frame the laws of physics are the same

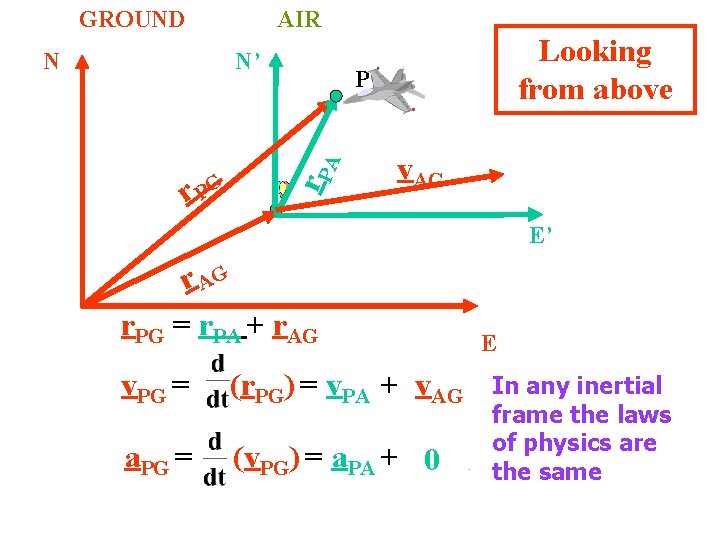
GROUND N’ r. P r PG Looking from above P A N AIR v. AG E’ r AG r. PG = r. PA + r. AG E v. PG = (r. PG) = v. PA + v. AG a. PG = (v. PG) = a. PA + In any inertial frame the laws of physics are a 0 AG the same

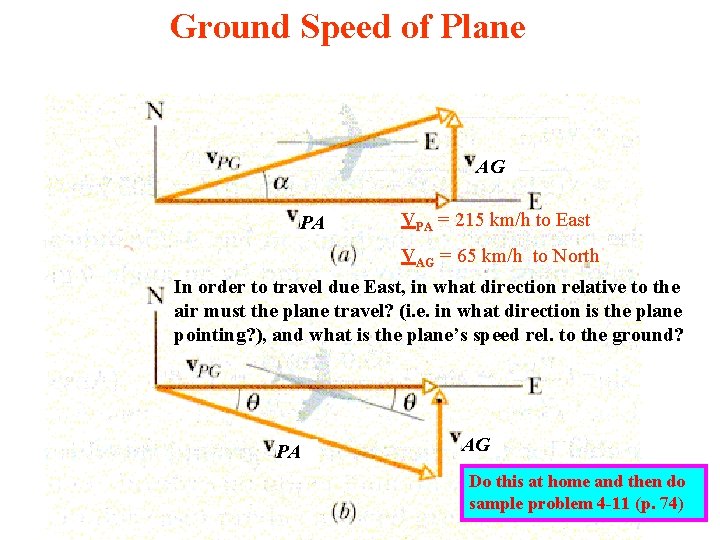
Ground Speed of Plane AG PA VPG = VPA + VAG VPA = 215 km/h to East VAG = 65 km/h to North PA Tan AG = 65/215 = 16. 8 o

Ground Speed of Plane AG PA VPA = 215 km/h to East VAG = 65 km/h to North In order to travel due East, in what direction relative to the air must the plane travel? (i. e. in what direction is the plane pointing? ), and what is the plane’s speed rel. to the ground? PA AG Do this at home and then do sample problem 4 -11 (p. 74)

A motorboat with its engine running at a constant rate travels across a river from Dock A, constantly pointing East. Flow X N A Y I will quiz you on this next lecture Z Compare the times taken to reach points X, Y, or Z when the river is flowing and when it is not. Your answer should include an explanation of what might affect the time taken to cross the river, and a convincing justification of your conclusion.

Here endeth the lesson lecture No. III

Isaac Newton 1642 -1727

Newton’s 1 st Law If a body is at rest, and no force acts on it, IT WILL REMAIN AT REST. If it is moving with a constant velocity, IT WILL CONTINUE TO DO SO If a body is moving at constant velocity, we can always find a reference frame where it is AT REST. At rest moving at constant velocity

Force The alteration of motion is ever proportional to the motive force impressed; and is made in If things dothenot needof pushing move direction the right lineto in which thatat force is impressed. what is the role of FORCE? ? ? constant velocity, An applied force changes the velocity of the body a F 1 a = m. F Inertial a mass = F/m F = ma The more massive a body is, the less it is accelerated by a given force.

Newton’s 2 nd Law a = F/m vector SUM of ALL EXTERNAL forces acting on the body a = _______ m F = ma vector SUM of ALL EXTERNAL forces acting on the body = ma

Newton’s 2 nd Law F=ma F = i. Fx + j. Fy + k. Fz a = iax + jay + kaz Fx=max Fy=may Fz=maz Applies to each component of the vectors

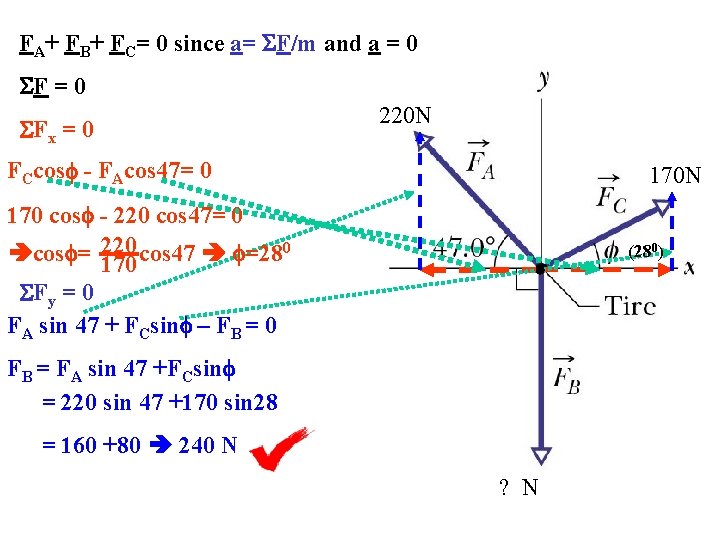
FA+ FB+ FC= 0 since a= F/m and a = 0 Fx = 0 Fy = 0 220 N FCcos - FAcos 47= 0 170 N 170 cos - 220 cos 47= 0 0 cos = 220 cos 47 =28 170 Fy = 0 FA sin 47 + FCsin – FB = 0 (280) FB = FA sin 47 +FCsin = 220 sin 47 +170 sin 28 = 160 +80 240 N ? N

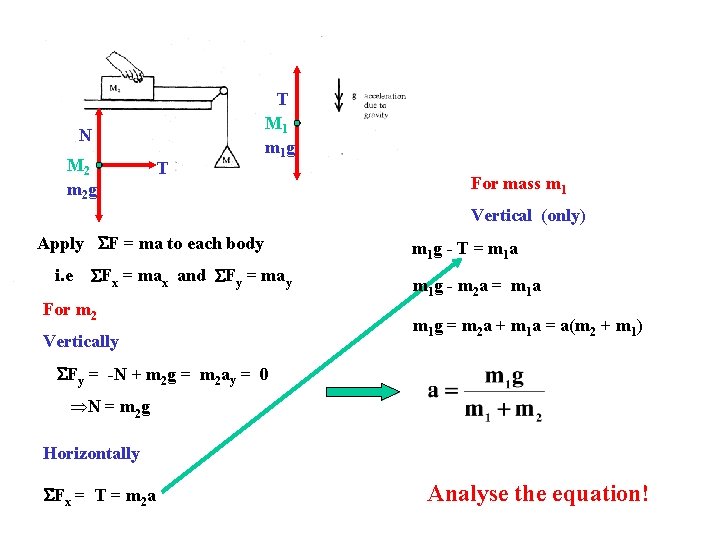
N M 2 m 2 g T T M 1 m 1 g For mass m 1 Vertical (only) Apply F = ma to each body i. e Fx = max and Fy = may For m 2 Vertically m 1 g - T = m 1 a m 1 g - m 2 a = m 1 a m 1 g = m 2 a + m 1 a = a(m 2 + m 1) Fy = -N + m 2 g = m 2 ay = 0 ÞN = m 2 g Horizontally Fx = T = m 2 a Analyse the equation!

2. 5 x 103 N 41% 26% 33% 3. 9 x 104 N

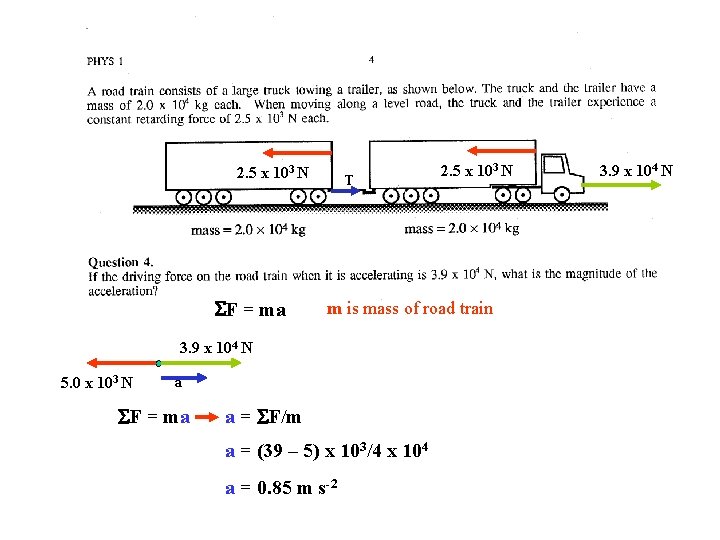
2. 5 x 103 N F = ma T m is mass of road train 3. 9 x 104 N 5. 0 x 103 N a F = ma 2. 5 x 103 N a = F/m a = (39 – 5) x 103/4 x 104 a = 0. 85 m s-2 3. 9 x 104 N

Don’t care! a=0 F = ma 2. 5 x 103 N T 2. 5 x 103 N m is mass of trailer! F is net force on TRAILER T 2. 5 x 103 N a=0 So F= 0 T - 2. 5 x 103 = 0 T = 2. 5 x 103 N

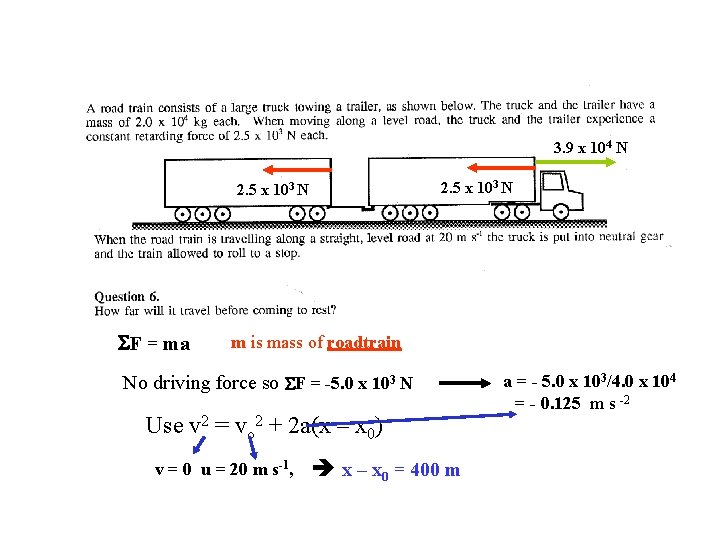
3. 9 x 104 N 2. 5 x 103 N F = ma m is mass of roadtrain No driving force so F = -5. 0 x 103 N Use v 2 = vo 2 + 2 a(x – x 0) v = 0 u = 20 m s-1, x – x 0 = 400 m a = - 5. 0 x 103/4. 0 x 104 = - 0. 125 m s -2