Summary Five numbers summary percentiles mean Box plot

Summary • Five numbers summary, percentiles, mean • Box plot, modified box plot • Robust statistic – mean, median, trimmed mean • outlier • Measures of variability • range, IQR, average absolute deviation, variation and standard deviation • Average distance between each data value and the mean is zero.

Standard deviation – empirical rule

population (census) vs. sample parameter (population) vs. statistic (sample)

Bias, sampling •

SRS • sampling with replacement • Generates independent samples. • Two sample values are independent if that we get on the first one doesn't affect what we get on the second. • sampling without replacement • Deliberately avoid choosing any member of the population more than once. • This type of sampling is not independent, however it is more common. • The error is small as long as 1. the sample is large 2. the sample size is no more than 10% of population size

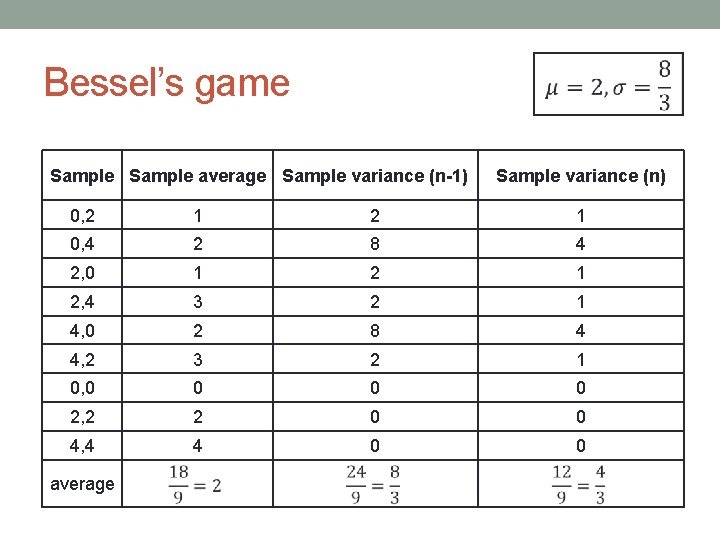
Bessel’s game Sample average Sample variance (n-1) Sample variance (n) 0, 2 1 0, 4 2 8 4 2, 0 1 2, 4 3 2 1 4, 0 2 8 4 4, 2 3 2 1 0, 0 0 2, 2 2 0 0 4, 4 4 0 0 average

Histogram revision • Distribution – the pattern of values in the data • Histogram – visualizing the distribution • We can see • whether the data tend to be close to the particular value • whether the data varies a lot or a little about the most common values • whether that variation tends to be more above or below the common values • whethere are unusually large or small values in the data

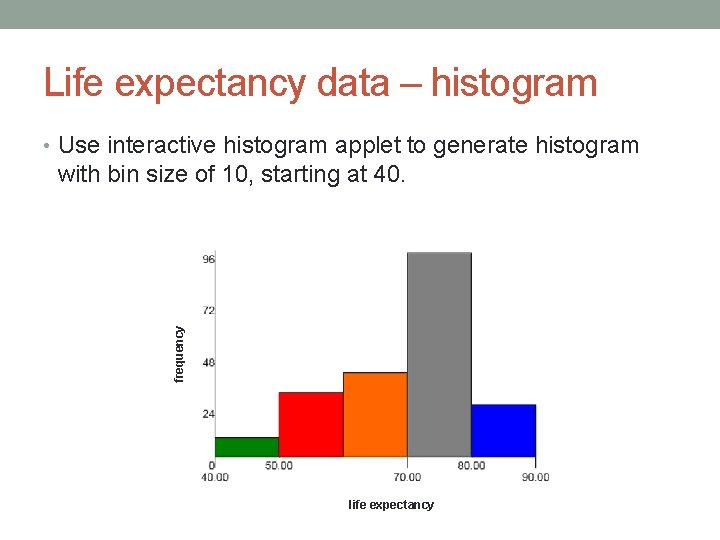
Life expectancy data – histogram • Use interactive histogram applet to generate histogram frequency with bin size of 10, starting at 40. life expectancy

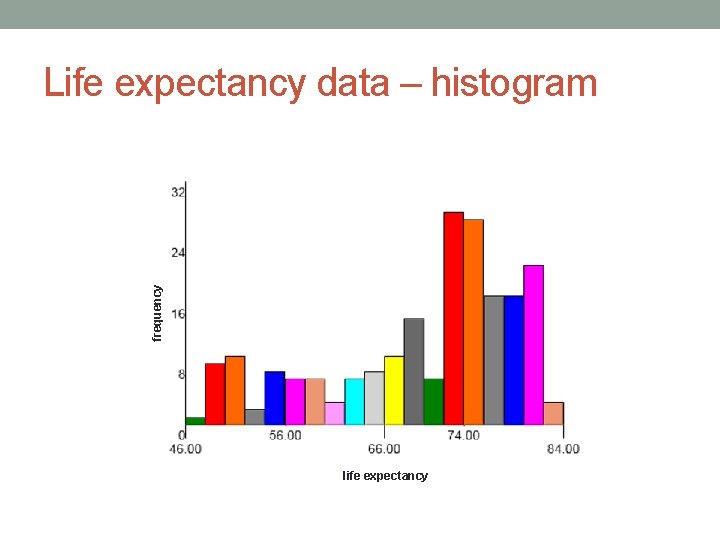
frequency Life expectancy data – histogram life expectancy

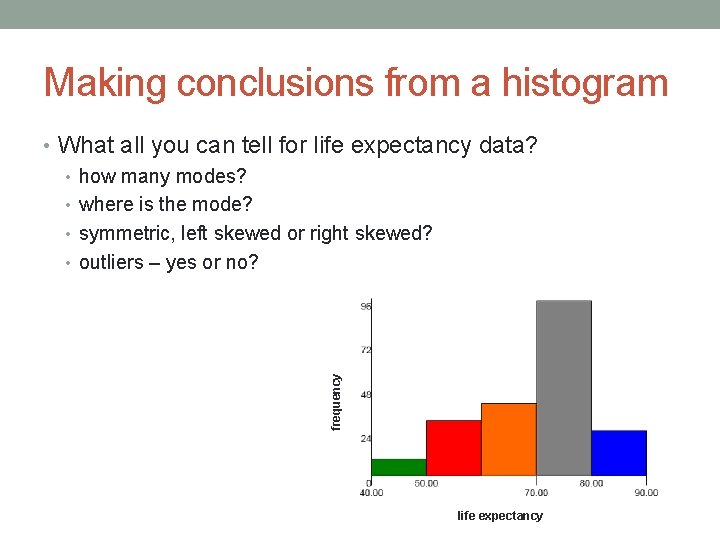
Making conclusions from a histogram frequency • What all you can tell for life expectancy data? • how many modes? • where is the mode? • symmetric, left skewed or right skewed? • outliers – yes or no? life expectancy

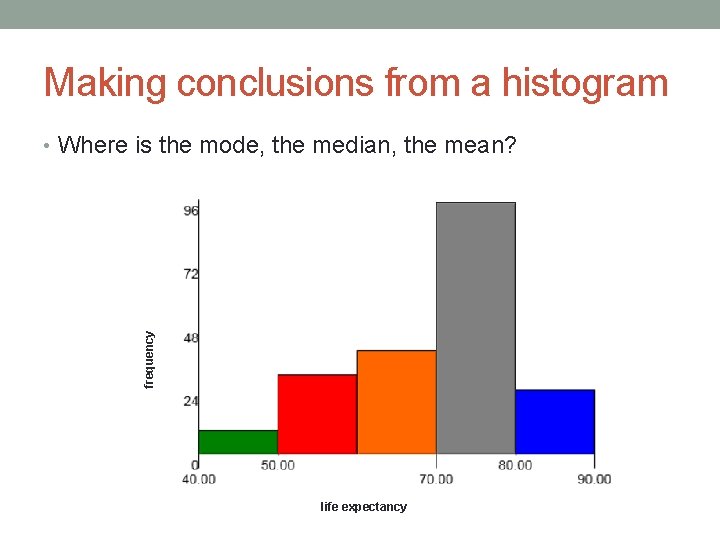
Making conclusions from a histogram frequency • Where is the mode, the median, the mean? life expectancy

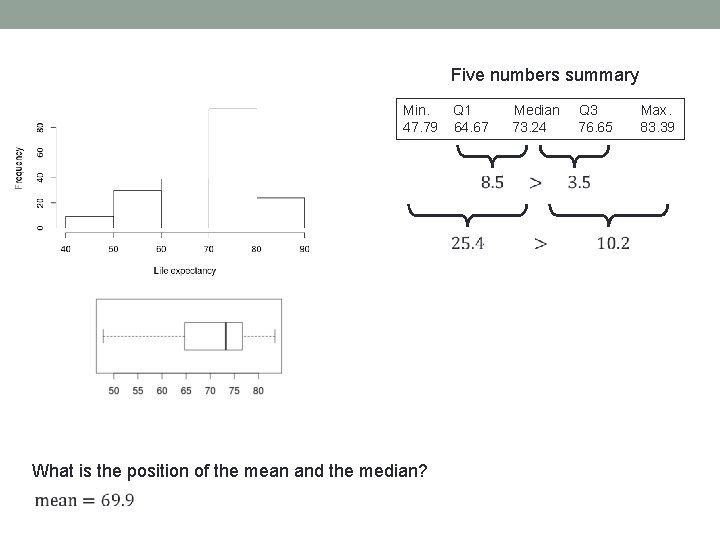
Five numbers summary Min. Q 1 Median Q 3 Max. 47. 79 64. 67 73. 24 76. 65 83. 39 What is the position of the mean and the median?

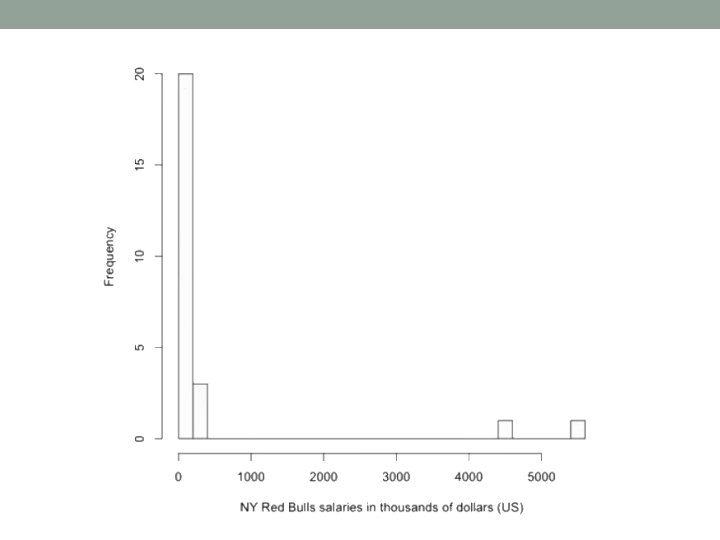
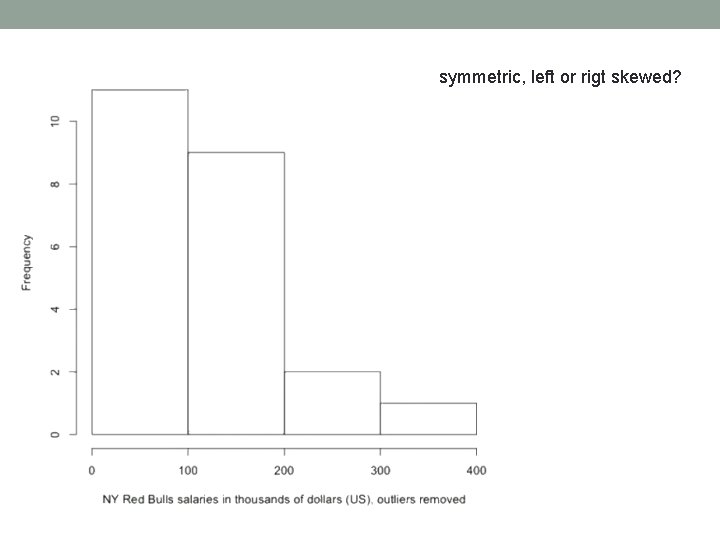
symmetric, left or rigt skewed?

STANDARDIZING normování

Playing chess • Pretend I am a chess player. • Which of the following tells you most about how good I am: 1. 2. 3. My rating is 1800. 8110 th place among world competitive chess players. Ranked higher than 88% of competitive chess players.

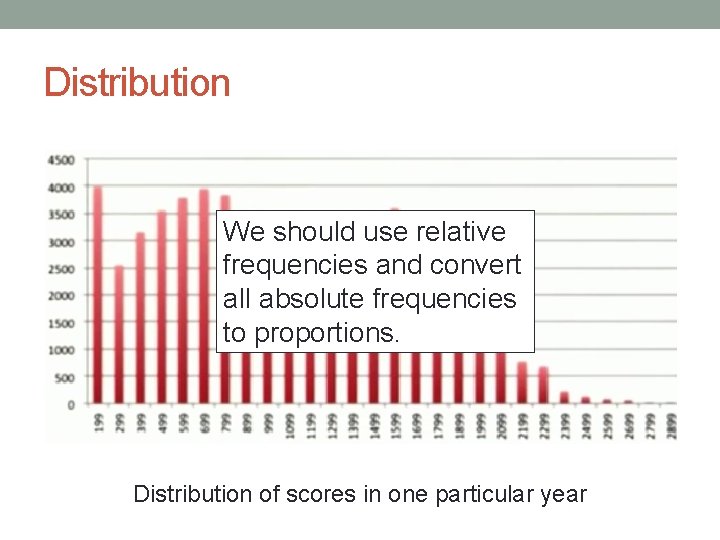
Distribution We should use relative frequencies and convert all absolute frequencies to proportions. Distribution of scores in one particular year

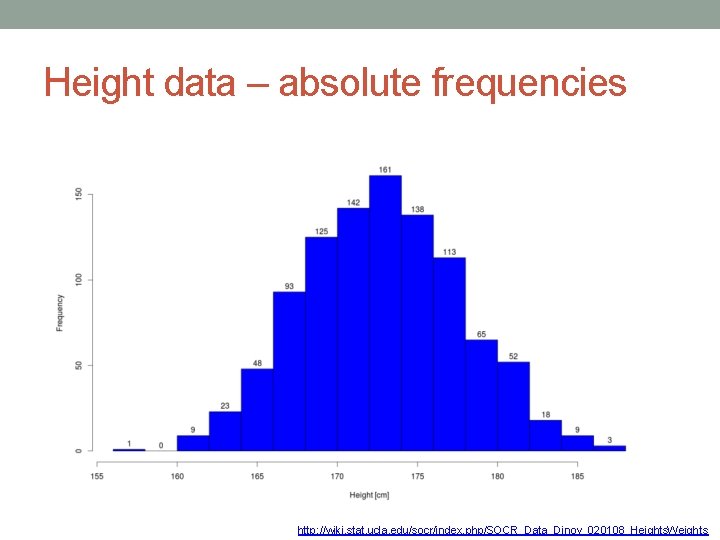
Height data – absolute frequencies http: //wiki. stat. ucla. edu/socr/index. php/SOCR_Data_Dinov_020108_Heights. Weights

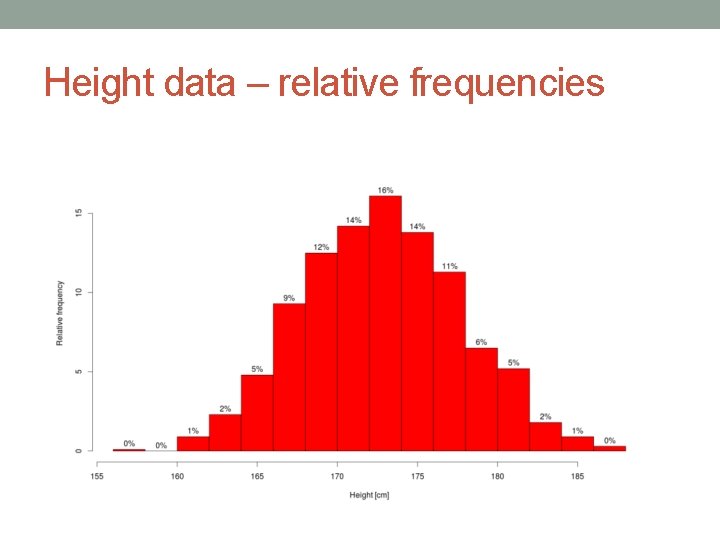
Height data – relative frequencies

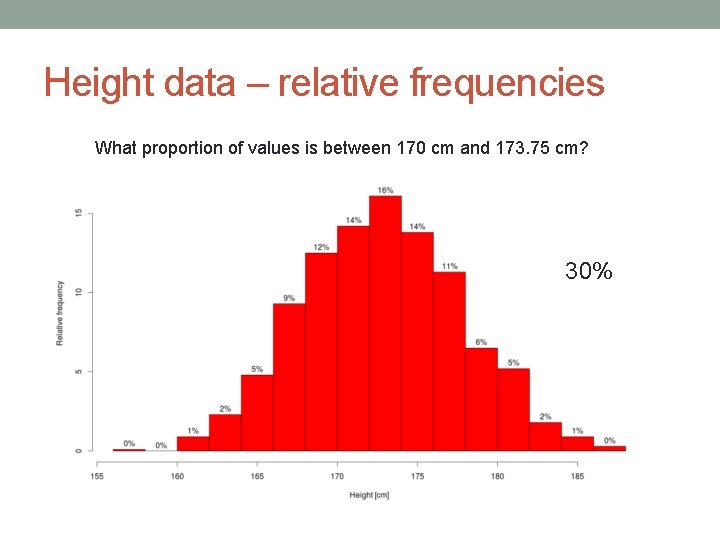
Height data – relative frequencies What proportion of values is between 170 cm and 173. 75 cm? 30%

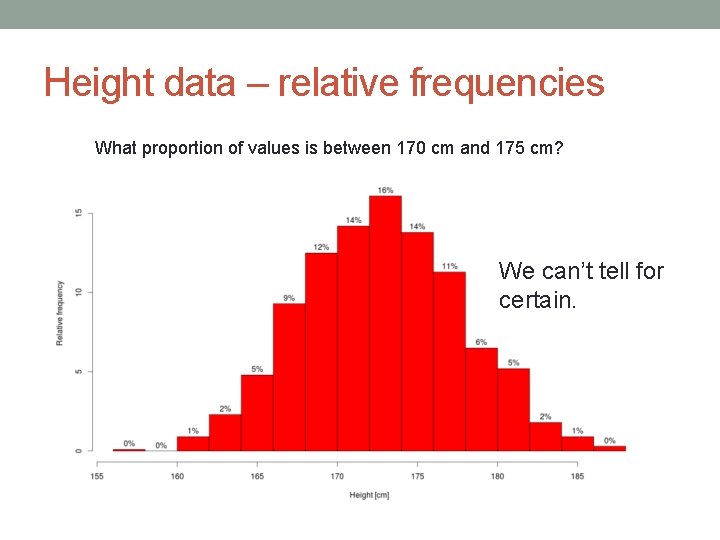
Height data – relative frequencies What proportion of values is between 170 cm and 175 cm? We can’t tell for certain.

• How should we modify data/histogram to allow us a more detail? 1. 2. 3. Adding more value to the dataset Increasing the bin size A smaller bin size

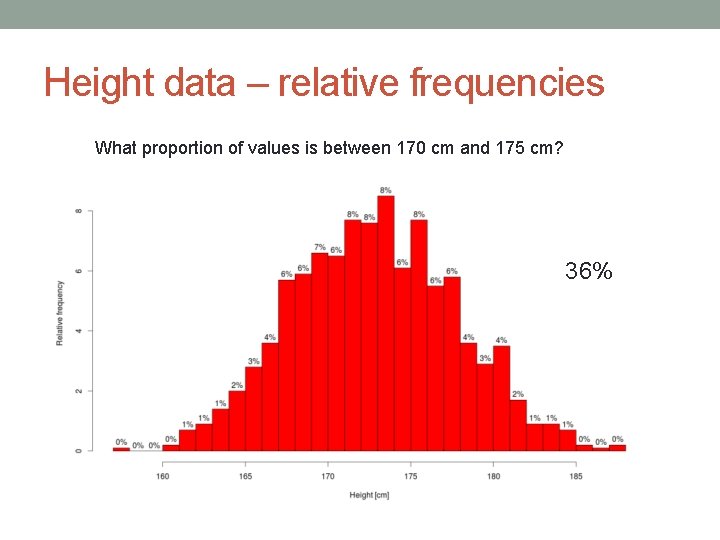
Height data – relative frequencies What proportion of values is between 170 cm and 175 cm? 36%

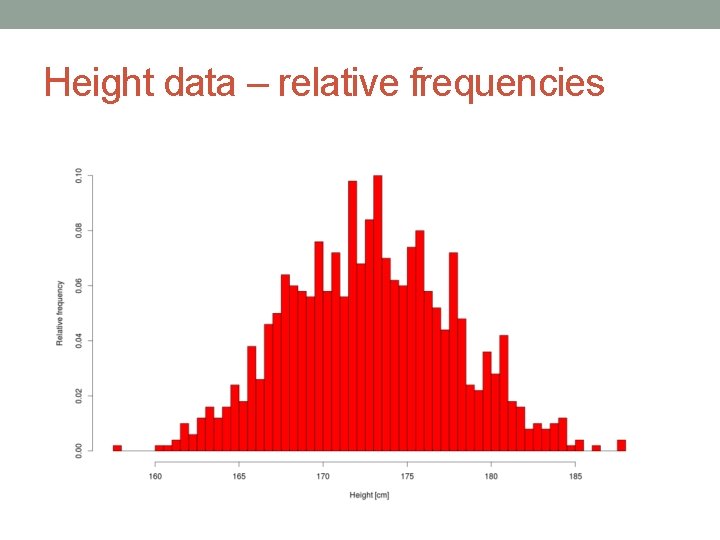
Height data – relative frequencies

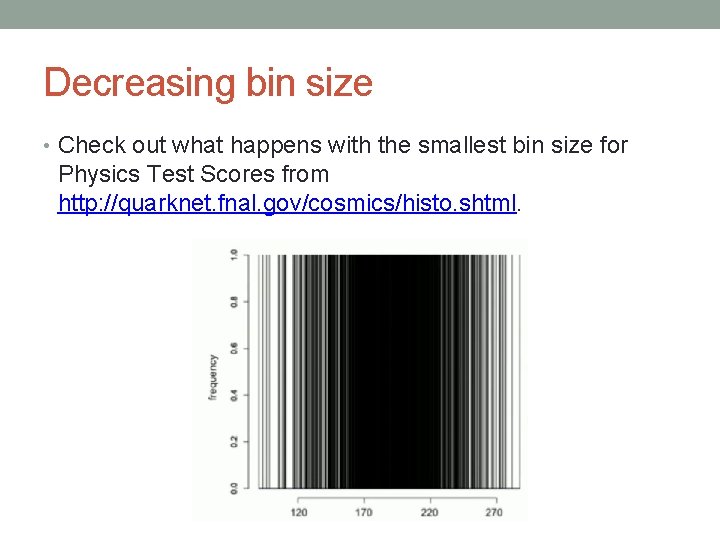
Decreasing bin size • Check out what happens with the smallest bin size for Physics Test Scores from http: //quarknet. fnal. gov/cosmics/histo. shtml.

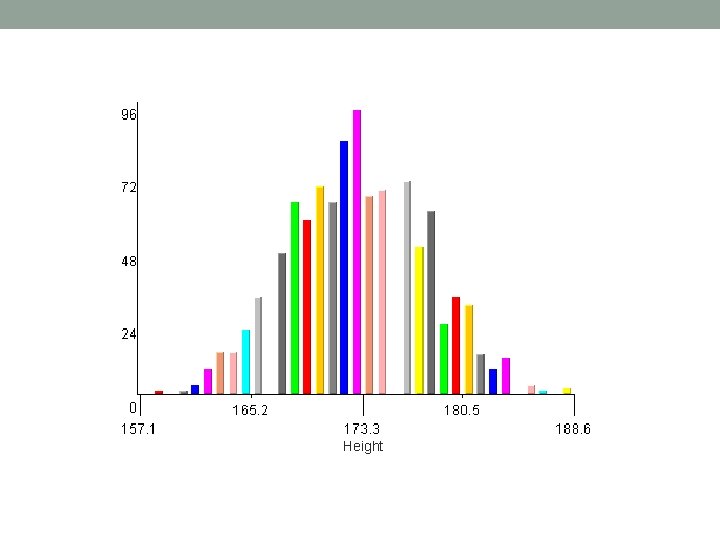
Height

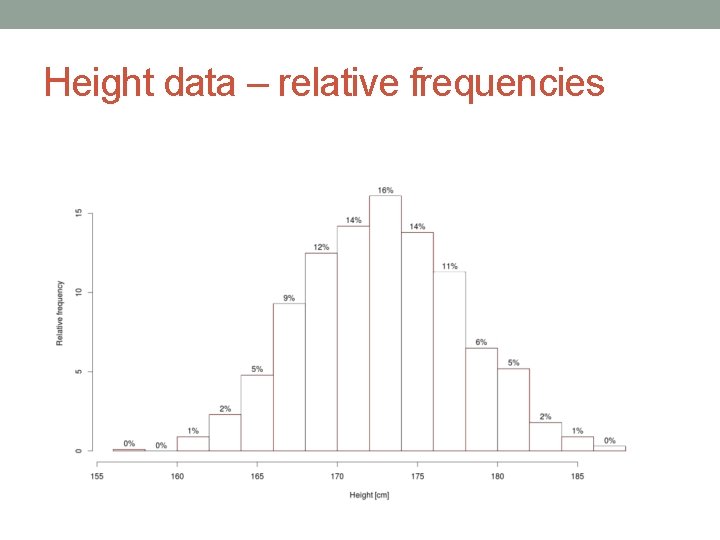
Height data – relative frequencies

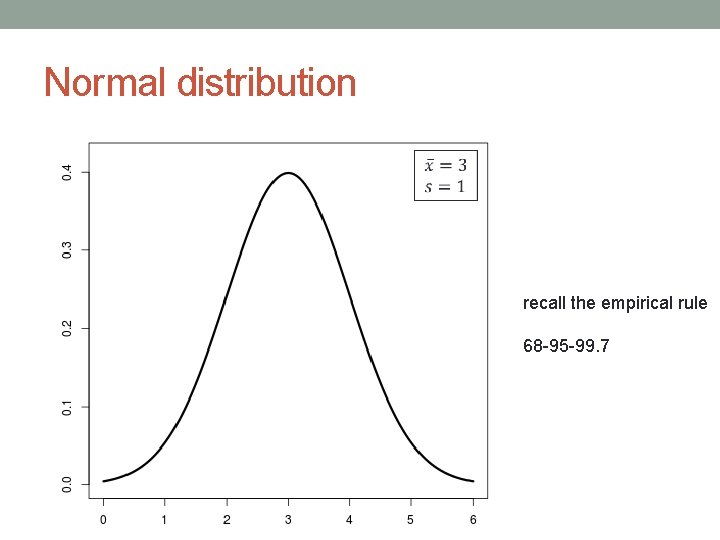
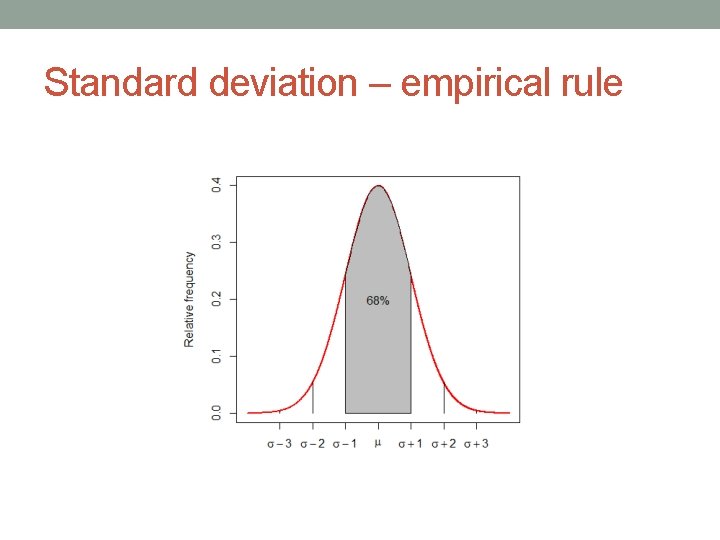
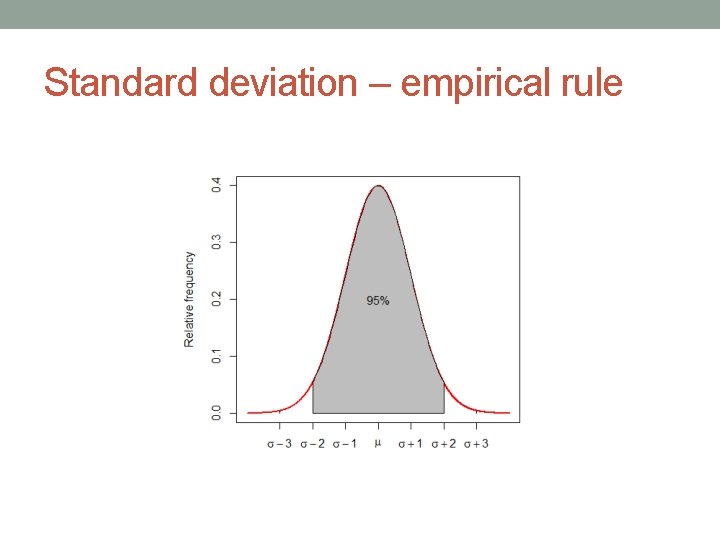
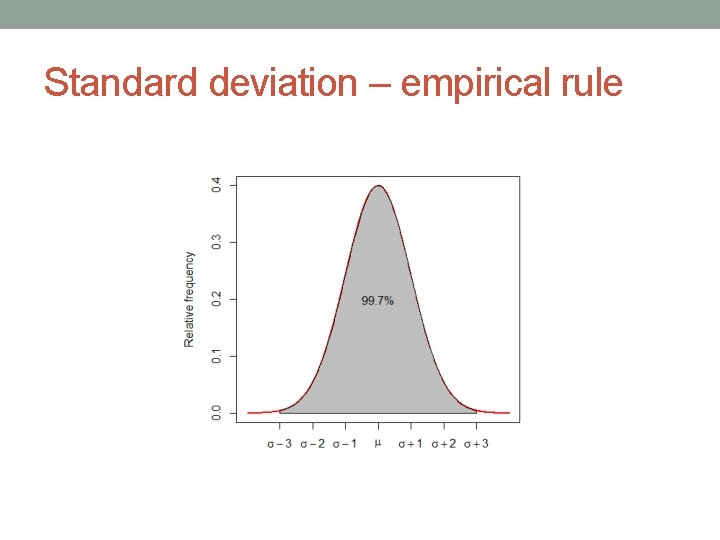
Normal distribution recall the empirical rule 68 -95 -99. 7

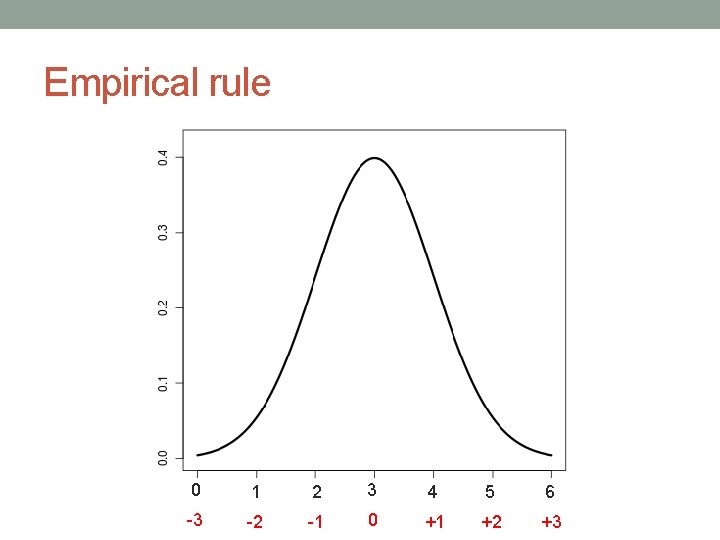
Empirical rule 0 1 2 3 4 5 6 -3 -2 -1 0 +1 +2 +3

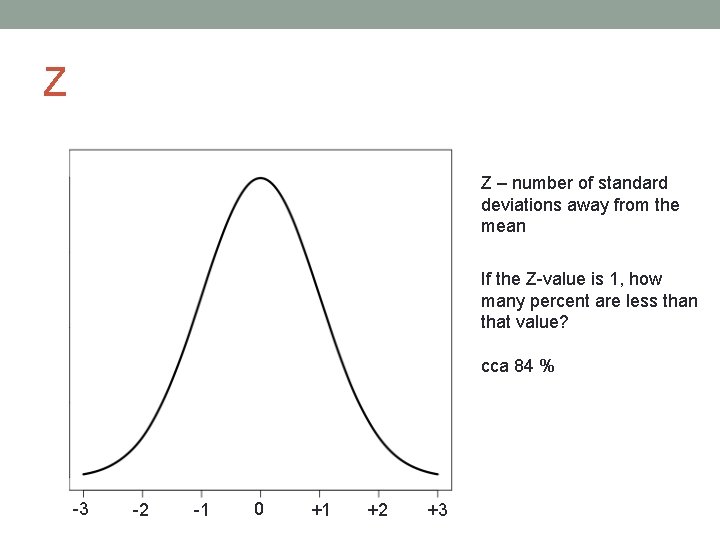
Z Z – number of standard deviations away from the mean If the Z-value is 1, how many percent are less than that value? cca 84 % -3 -2 -1 0 +1 +2 +3

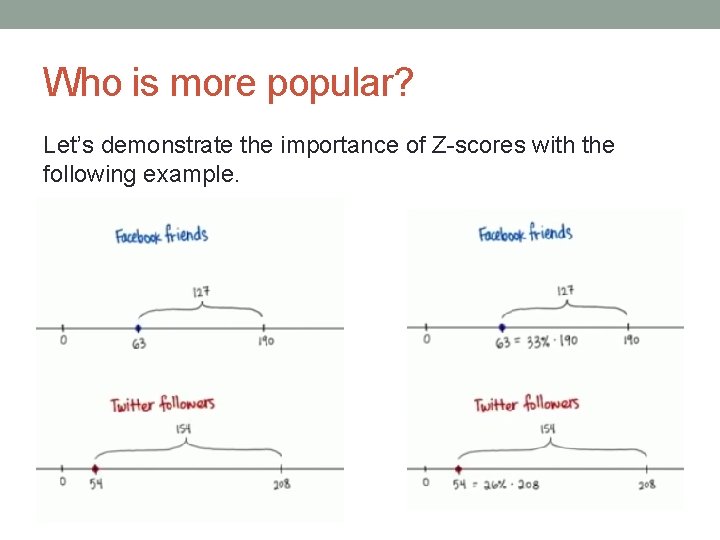
Who is more popular? Let’s demonstrate the importance of Z-scores with the following example.

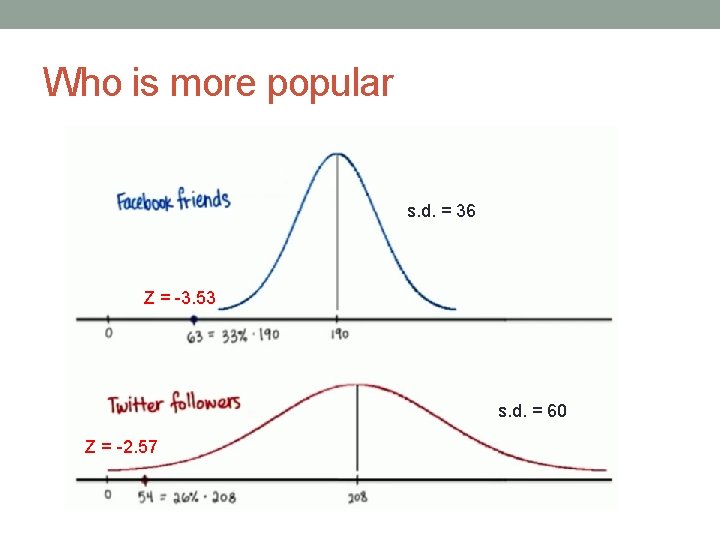
Who is more popular s. d. = 36 Z = -3. 53 s. d. = 60 Z = -2. 57

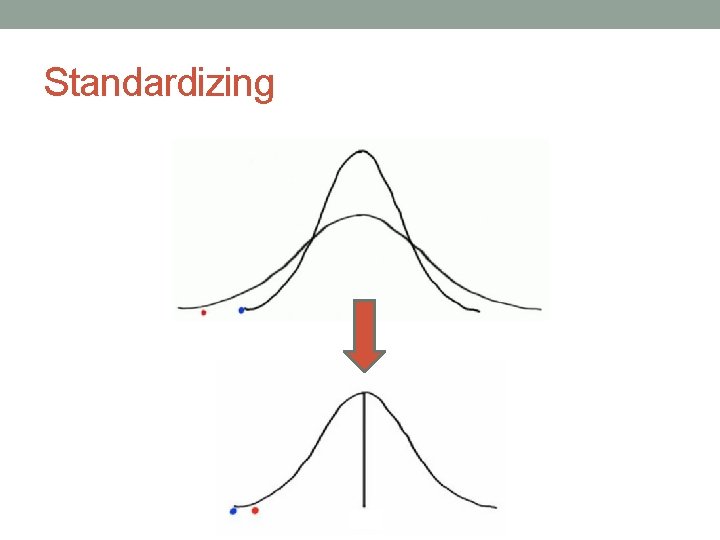
Standardizing

Formula •

Quiz • What does a negative Z-score mean? 1. The original value is negative. 2. The original value is less than mean. 3. The original value is less than 0. 4. The original value minus the mean is negative.

Quiz II • If we standardize a distribution by converting every value to a Z-score, what will be the new mean of this standardized distribution? • If we standardize a distribution by converting every value to a Z-score, what will be the new standard deviation of this standardized distribution?

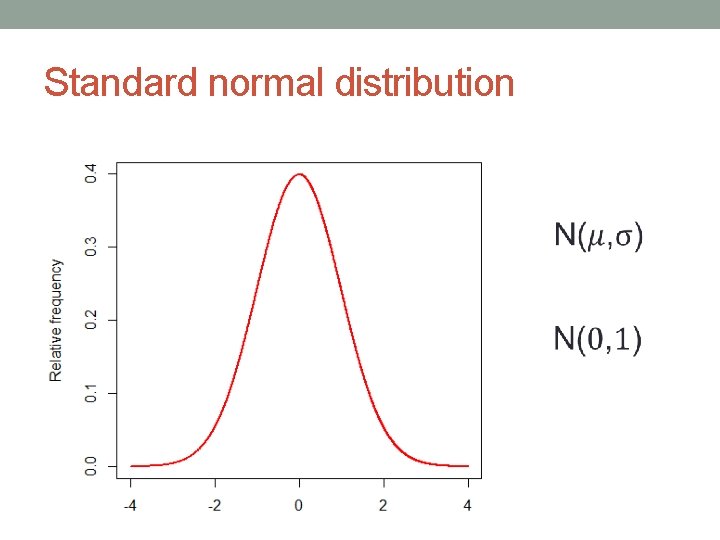
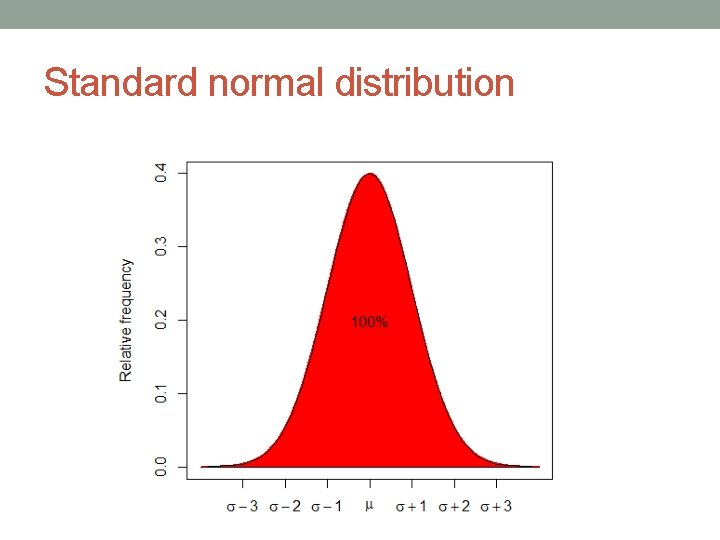
Standard normal distribution

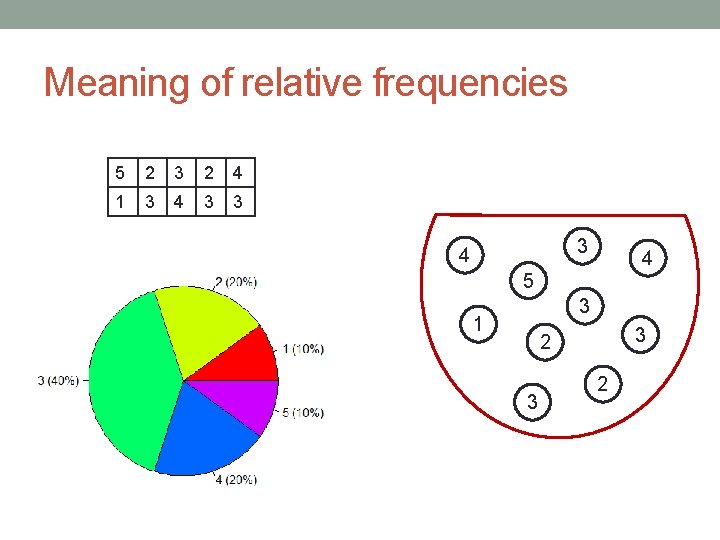
Meaning of relative frequencies 5 2 3 2 4 1 3 4 3 3 3 4 4 5 3 1 3 2

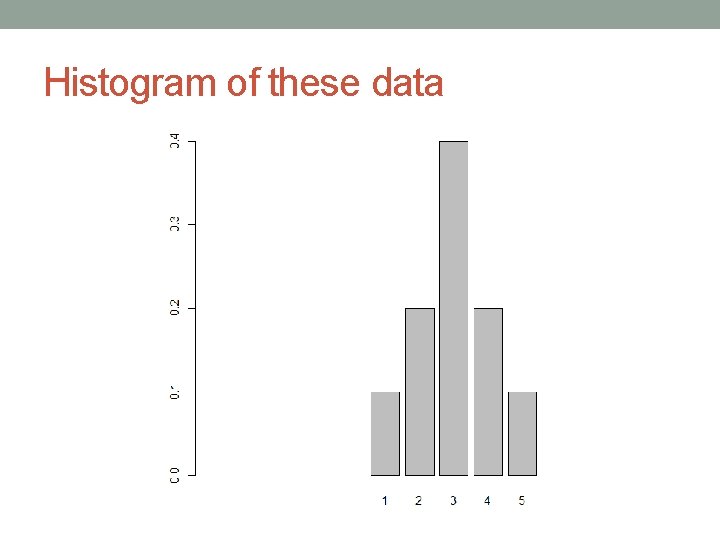
Histogram of these data

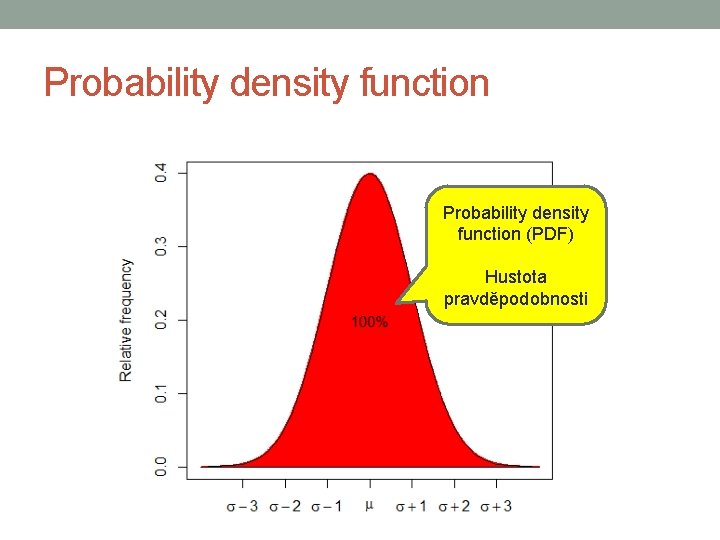
Probability density function (PDF) Hustota pravděpodobnosti

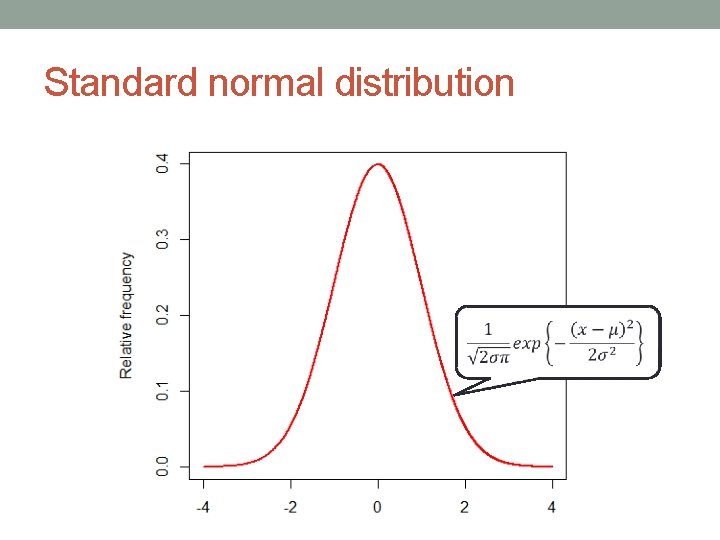
Standard normal distribution