Summary 1 Some history 2 Antiparticles 3 Standard

Summary 1. Some history 2. Antiparticles 3. Standard Model of Particles (SM) Discrete symmetries, CP violation, Connection with Cosmology Fermionic mass generation mechanism, 4. Why do we think that the SM is not the final word ? 5. How do we produce particles? 6. How do we measure particles ? 7. Conclusions A. Bay Beijng October 2005 1

e. m. charge [e] 0 The Standard Model -1 MATTER INTERACTIONS ne nm nt e- m- t- 2/3 u - 1/3 d c Quarks s t b Spin 1/2 Weak : W+ W- Z E. M. : photon Strong : gluons Spin 1 The SM incorporates: QED: photon exchange between charged particles Weak (Flavour-Dynamics): exchange of W± and Z QCD: gluon exchange between quarks do not forget antiparticles. . . ! A. Bay Beijng October 2005 2

Summary of this section Symmetries Parity (P), Charge Conjugation (C) and Time reversal (T) P and C violation Baryogenesis CP & T violation Experiments Conclusion A. Bay Beijng October 2005 3

Discrete symmetries left right Parity: Charge particle conjugation antiparticle Temporal inversion A. Bay Beijng October 2005 4

Discrete symmetries P and C P: (x, y, z) -> (-x, -y, -z). angular momentum, spin. C: charge -> -charge. e. m. interactions are P & C invariant A. Bay Beijng October 2005 5

What about T ? If x(t) is solution of F = m d 2 x/dt 2 then x(-t) is also a solution (ex. : billiard balls) Ok with electrodynamics: A. Bay Beijng October 2005 6

Parity: (x, y, z) (-x, -y, -z) 1848 L. Pasteur discovers the property of optical isomerism. Mirror symmetry The synthesis of the lactic acid in the lab gives a "racemic" mixture: Nleft molecules = Nright molecules (within statistic fluctuations) Asymmetry = This reflects the fact that e. m. interaction is M (and P) invariant A. Bay Beijng October 2005 7

Parity violation in biology Humans are mostly right handed: Asymmetry A = (NR-NL)/(NR+NL) ≈ 0. 9 “ 90% Parity violation" if n s if sn Lemmon and orange flavours are produced by the two "enantiomers" of the same molecule. A. Bay Beijng October 2005 8

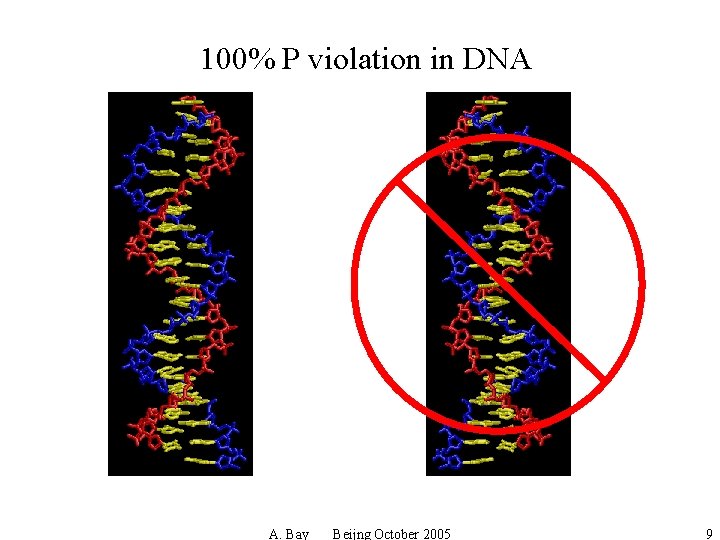
100% P violation in DNA A. Bay Beijng October 2005 9

Too much symmetry. . . LR LL RR A. Bay Beijng October 2005 10

Partial R-L symmetry in Rome ? Bacchus, Arianna ? MUSEE ROMAIN DE NYON A. Bay Beijng October 2005 11

Some asymmetry introduces more dynamics A. Bay Beijng October 2005 12

P conserved in e. m. and strong interacctions 1924 O. Laporte classified the wavefunctions of an atom as either even or odd, parity +1 or -1. In e. m. atomic transitions a photon of parity -1 is emitted. The atomic wavefunction must change to keep the overall symmetry constant (Eugene Wigner, 1927) : Parity is conserved in e. m. transitions This is also true for e. m. nuclear or sub-nuclear processes (within uncertainties). H(strong) and H(e. m. ) are considered parity conserving. A. Bay Beijng October 2005 13

Parity in weak interactions * E. Fermi, 1949 model of W interactions: P conservation assumed C. F. Powell, . . . observation of two apparently identical particles "tau" and "theta" weakly decaying tau 3 pions theta 2 pions which indicates P(tau) = -1 and P(theta) = + 1 If Parity holds "tau" and "theta" cannot be the same particle. * A. Bay Beijng October 2005 14

Parity in weak interactions. 2 Lee and Yang make a careful study of all known experiments involving weak interactions. They conclude "Past experiments on the weak interactions had actually no bearing on the question of parity conservation" Question of Parity Conservation in Weak Interactions T. D. Lee Columbia University, New York C. N. Yang Brookhaven National Laboratory, Upton, New York The question of parity conservation in beta decays and in hyperon and meson decays is examined. Possible experiments are suggested which might test parity conservation in these interactions. Phys. Rev. 104, 254– 258 (1956) A. Bay Beijng October 2005 15

Co 60 1956 C. S. Wu et al. execute one of the experiments proposed by Lee and Yang. Co 60 at 0. 01 K in a B field. In a P reversed Word: P: Jp a - Jp P symmetry implies m = 0 m was found 0 P is violated A. Bay Beijng October 2005 J p Co Observables: a "vector" : momentum p of beta particles an "axial-vector" : spin J of nucleus (from B). Compute m = <Jp> Co p 16

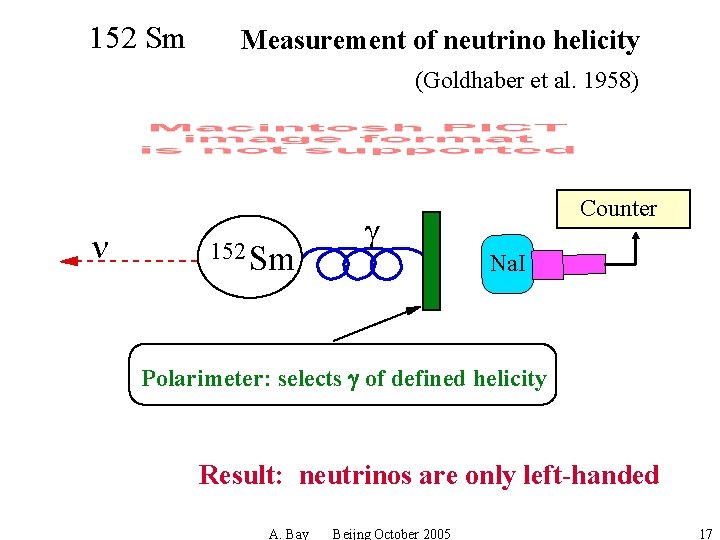
152 Sm Measurement of neutrino helicity (Goldhaber et al. 1958) n 152 Sm g Counter Na. I Polarimeter: selects g of defined helicity Result: neutrinos are only left-handed A. Bay Beijng October 2005 17

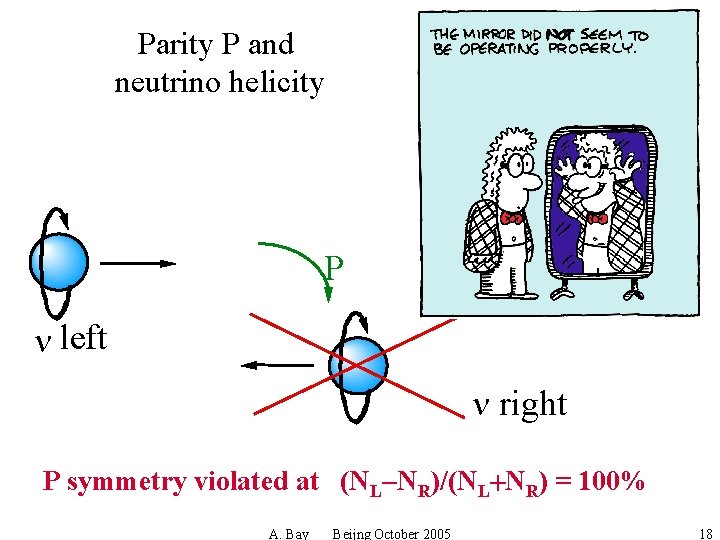
Parity P and neutrino helicity P n left n right P symmetry violated at (NL-NR)/(NL+NR) = 100% A. Bay Beijng October 2005 18

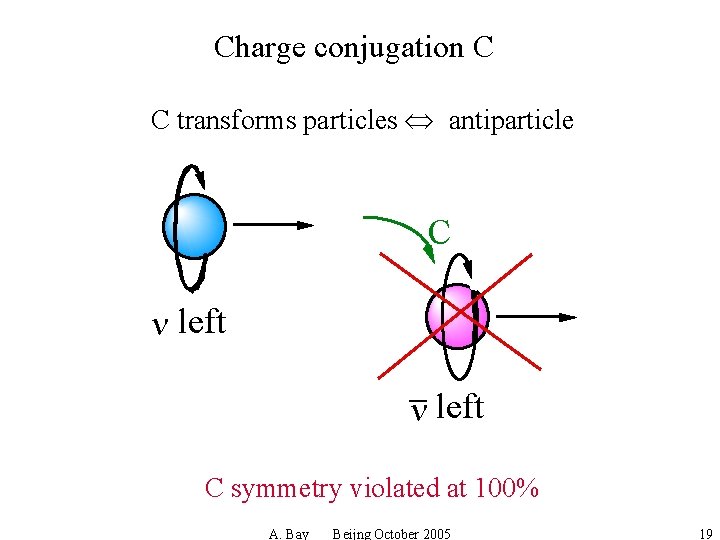
Charge conjugation C C transforms particles antiparticle C n left C symmetry violated at 100% A. Bay Beijng October 2005 19

Last chance: combine C and P ! CP left right Is our Universe CP symmetric ? A. Bay Beijng October 2005 20

(A)symmetry in the Universe matter Big Bang antimatter time Big Bang produced an equal amount of matter and antimatter A. Bay Today: we live in a matter dominated Universe Beijng October 2005 21

Big Bang models are matter/antimatter symmetric Baryo genesis Where is ANTIMATTER today? 1) Anti-Hydrogen has been produced at CERN: antimatter can exist. 2) Moon is made with matter. Idem for the Sun and all the planets. 3) In cosmics we observe e+ and antiprotons, but rate is compatible with secondary production. 4) No sign of significant of e+e- annihilation in Local Cluster. 5) Assuming Big Bang models OK, statistical fluctuations cannot be invoked to justify observations. No known mechanism to separate matter and antimatter at very large scale e+e- annihilation in the Galaxy A. Bay Beijng October 2005 22

AMS sensitivity (0. 5 - 20 Ge. V): He/He ~10 -9 C/C ~10 -8 A. Bay Beijng October 2005 23

Baryogenesis. 2 Today (age of Univers 10 -20 109 years): no significant amount of antimatter has been observed. The visible Universe is maid of protons, electrons and photons The N of photons is very large compared to p and e 2. 5 10 -10£ Nprotons Nphotons £ 5 10 -8 rmatter =0. 1 r. C =1 10 -6 Ge. V/cm 3 10 -6 p/cm 3 A. Bay Beijng October 2005 24

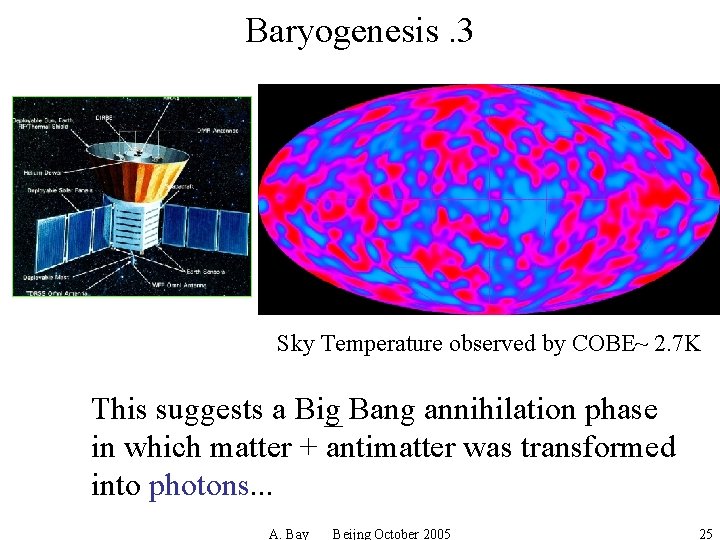
Baryogenesis. 3 Sky Temperature observed by COBE~ 2. 7 K 3 This suggests a Big 2 Bang k. T annihilation phase N 2. 7 1. 202 2 ( ) = 412 photons/cm 3 ch in which matter + pantimatter was transformed into photons. . . A. Bay Beijng October 2005 25

Baryogenesis. 4 A. Bay Beijng October 2005 26

Baryo genesis. 5 Starting from a perfectly symmetric Universe: 3 rules to induce asymmetry during evolution 1) $ processes which violate baryonic number conservation: B(t=0) = 0 B(today)>0 B violation is unavoidable in GUT. Andrej Sakarov 1967 2) Interactions must violate C and CP. C violated in Weak Interactions. . CP violation observed in K and B decays 3) System must be out of thermal equilibrium Universe expands (but was the change fast enough ? ) A. Bay Beijng October 2005 27

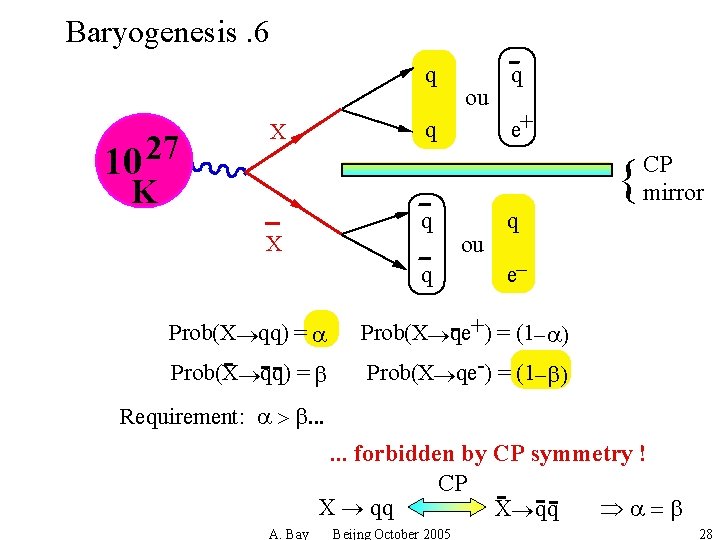
Baryogenesis. 6 q 27 10 K ou q X q e+ { q X q Prob(X qq) = a - -qq) - =b Prob(X ou CP mirror q e- - +) = (1 -a) Prob(X qe-) = (1 -b) Requirement: a > b. . . forbidden by CP symmetry ! CP - qq -- a = b X qq X A. Bay Beijng October 2005 28

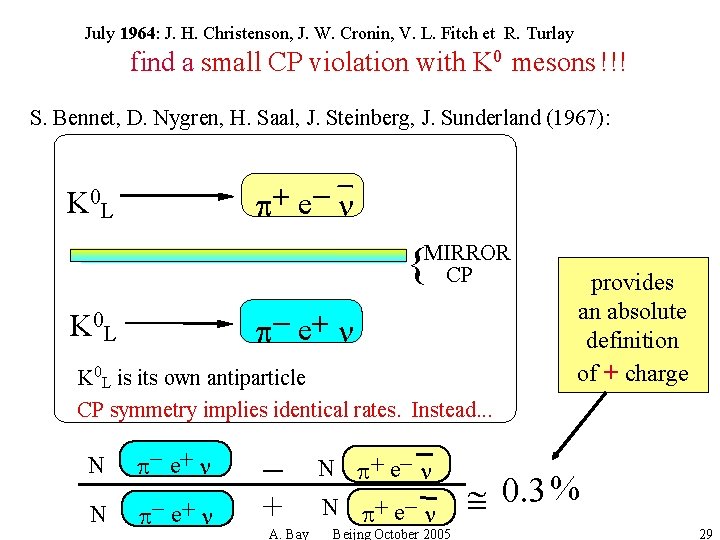
July 1964: J. H. Christenson, J. W. Cronin, V. L. Fitch et R. Turlay find a small CP violation with K 0 mesons !!! S. Bennet, D. Nygren, H. Saal, J. Steinberg, J. Sunderland (1967): p+ e- n K 0 L {MIRROR CP p- e+ n K 0 L is its own antiparticle CP symmetry implies identical rates. Instead. . . N p- e+ n + A. Bay N p+ e- n Beijng October 2005 provides an absolute definition of + charge 0. 3 % 29

CP violation experiment A. Bay Beijng October 2005 30

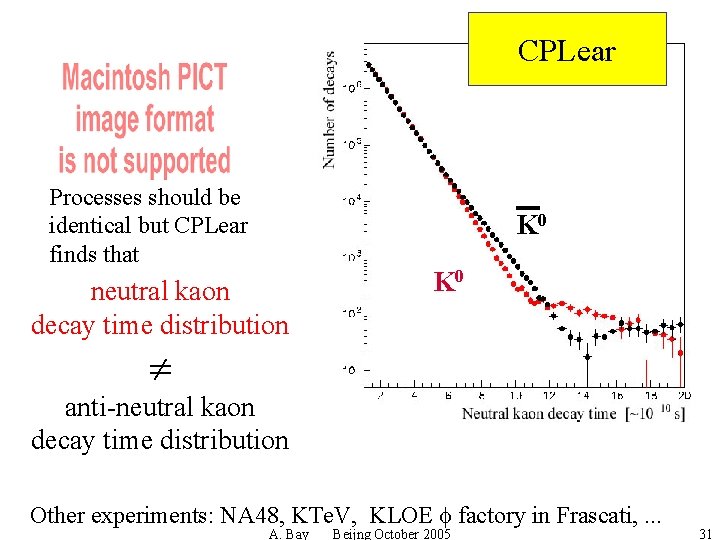
CPLear Processes should be identical but CPLear finds that K 0 neutral kaon decay time distribution K 0 anti-neutral kaon decay time distribution Other experiments: NA 48, KTe. V, KLOE f factory in Frascati, . . . A. Bay Beijng October 2005 31

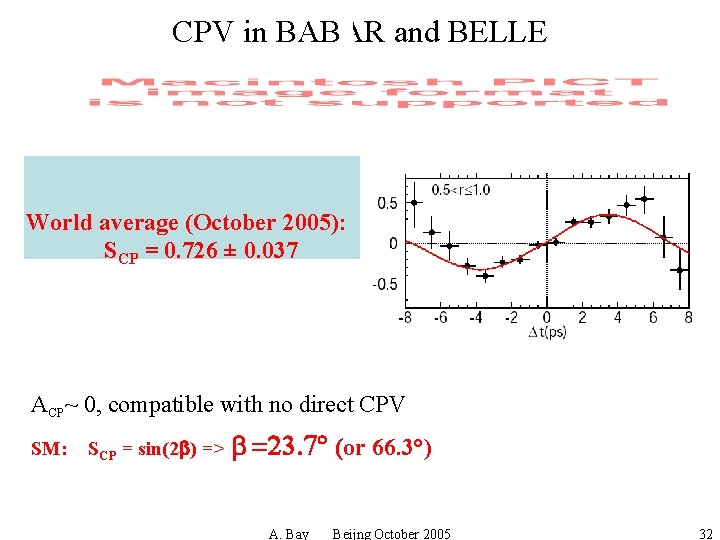
CPV in BABAR and BELLE World average (October 2005): SCP = 0. 726 ± 0. 037 ACP~ 0, compatible with no direct CPV SM: SCP = sin(2 b) => b =23. 7° (or 66. 3°) A. Bay Beijng October 2005 32

Origin of CP violation Hamiltonian H = H 0 + HCP with HCP responsible for CP violation. Let's take HCP = g. H + g*H† where g is some coupling. The second term is required by hermiticity. If under CP: H H† that is CP H CP† = H† then CP HCP CP† = CP (g. H + g*H†) CP† = g. H† + g*H CP invariance : HCP = CP HCP CP† g. H + g*H† = g. H† + g*H The conclusion is that CP is violated if g g* i. e. g non real CP violation is associated to the existence of phases in the hamiltonian. A. Bay Beijng October 2005 33

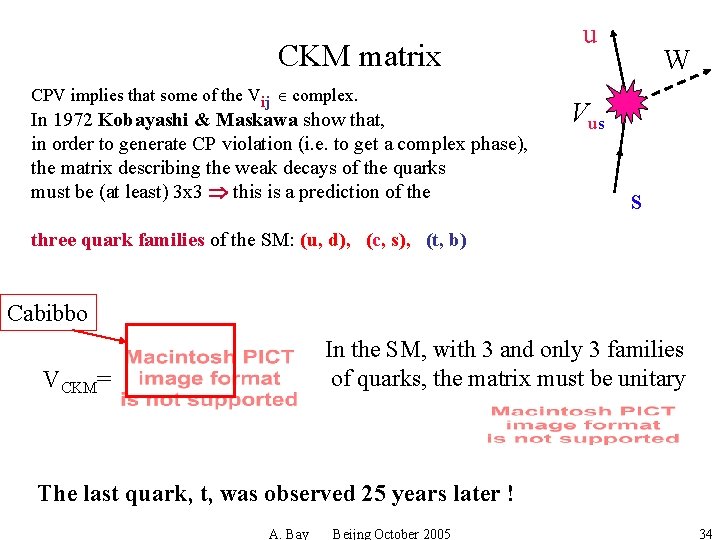
CKM matrix CPV implies that some of the Vij complex. In 1972 Kobayashi & Maskawa show that, in order to generate CP violation (i. e. to get a complex phase), the matrix describing the weak decays of the quarks must be (at least) 3 x 3 this is a prediction of the u W Vus s three quark families of the SM: (u, d), (c, s), (t, b) Cabibbo In the SM, with 3 and only 3 families of quarks, the matrix must be unitary VCKM= The last quark, t, was observed 25 years later ! A. Bay Beijng October 2005 34

CKM matrix in the SM L = L W, Z + L H + L Fermions + L interaction L Fermions contains the (Yukawa) mass terms: MU and MD complex matrices, diagonalized by a couple of non-singular matrices, to get the physical mass values: A. Bay Beijng October 2005 35

CKM matrix. 2 After the transformation (idem for D quarks) e. m. and neutral currents unaffected. The charged currents are modified: u "mixing matrix" V unitary A. Bay W Vus Beijng October 2005 s 36

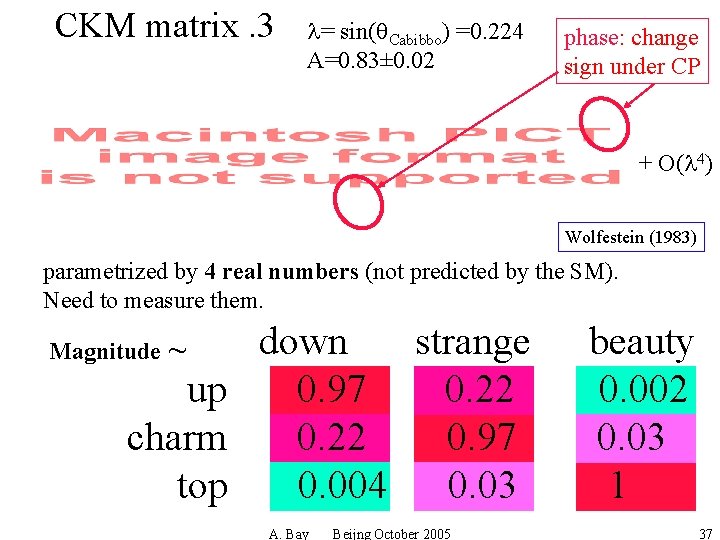
CKM matrix. 3 l= sin(q. Cabibbo) =0. 224 A=0. 83± 0. 02 phase: change sign under CP + O(l 4) Wolfestein (1983) parametrized by 4 real numbers (not predicted by the SM). Need to measure them. down strange up 0. 97 0. 22 charm 0. 22 0. 97 top 0. 004 0. 03 Magnitude ~ A. Bay Beijng October 2005 beauty 0. 002 0. 03 1 37

CKM matrix. 4 Today precision from direct measurements, no unitarity imposed: s(|Vij|)/|Vij| ~ down strange up 0. 1% 1% charm 7% 15% top 20% ? % A. Bay Beijng October 2005 beauty 17% 5% 29% 38

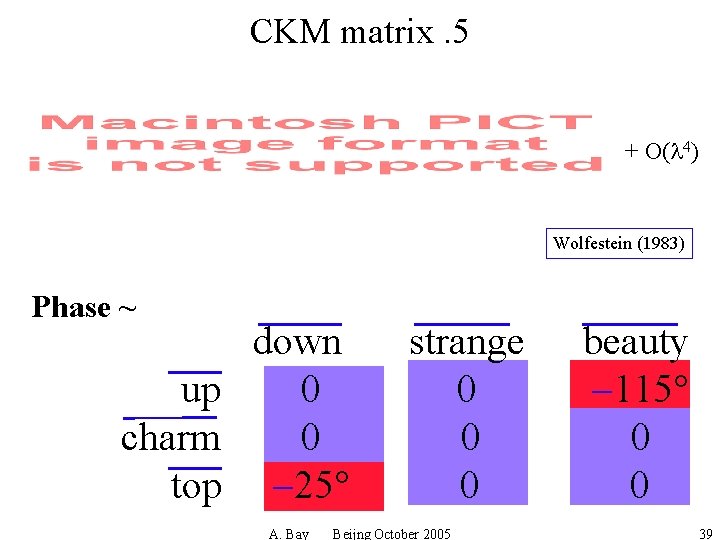
CKM matrix. 5 + O(l 4) Wolfestein (1983) Phase ~ down up 00 charm 00 top -25° A. Bay strange 0 0 0 Beijng October 2005 beauty -115° 0 0 39

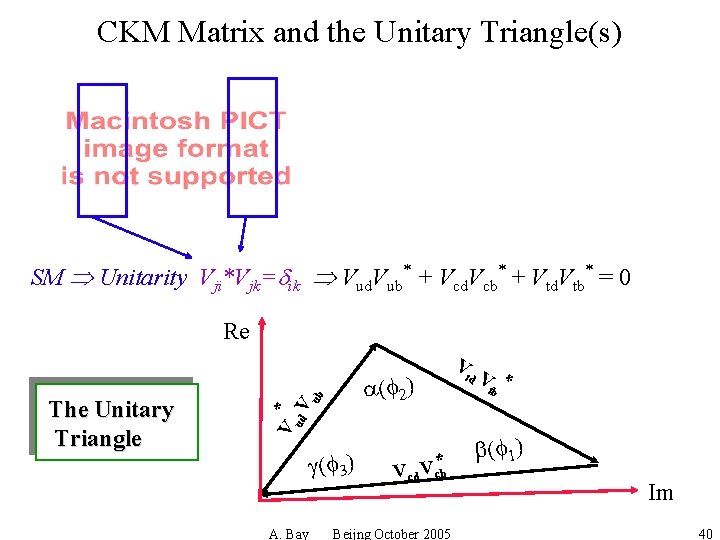
CKM Matrix and the Unitary Triangle(s) SM Unitarity Vji*Vjk=dik Vud. Vub + Vcd. Vcb + Vtd. Vtb = 0 Re ud V ub * td V tb a(f 2) V The Unitary Triangle V g(f 3) A. Bay V* Vcd cb Beijng October 2005 * b(f 1) Im 40

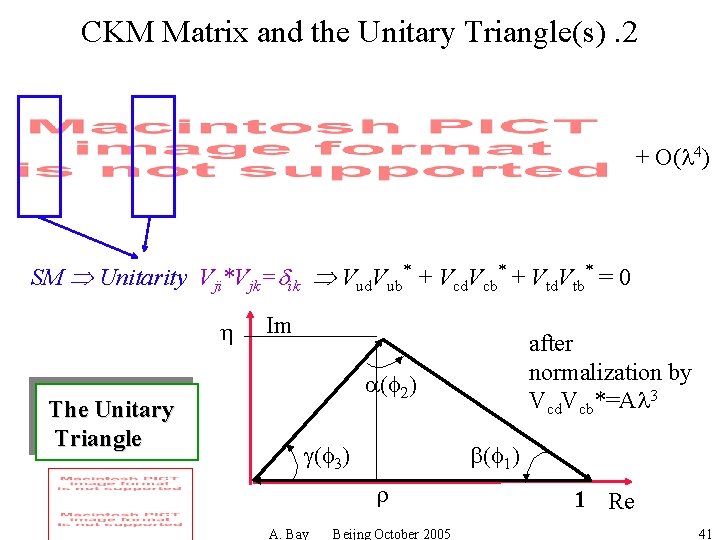
CKM Matrix and the Unitary Triangle(s). 2 + O(l 4) SM Unitarity Vji*Vjk=dik Vud. Vub + Vcd. Vcb + Vtd. Vtb = 0 h The Unitary Triangle Im after normalization by Vcd. Vcb*=Al 3 a(f 2) g(f 3) b(f 1) r A. Bay Beijng October 2005 1 Re 41

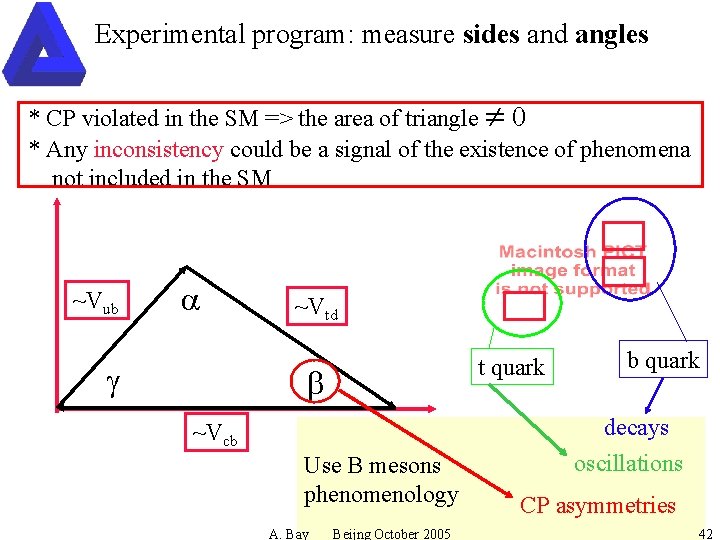
Experimental program: measure sides and angles * CP violated in the SM => the area of triangle 0 * Any inconsistency could be a signal of the existence of phenomena not included in the SM ~Vub a g ~Vtd t quark b b quark decays ~Vcb Use B mesons phenomenology A. Bay Beijng October 2005 oscillations CP asymmetries 42

Why do we expect some NEW PHYSICS ? * SM has 18 free parameters (more with massive neutrini), in particular masses and CKM parameters are free. * Some of the neutrinos have masses>0. * Why the electric charge is quantized ? * The choice of SU(2)U(1) is arbitrary. * Gravitation is absent. * Problems in Cosmology: What is the nature of dark matter and dark energy ? Baryogenesis does not work in the SM: The SM amount of CP violation is too low The requirement of non-equilibrium cannot be obtained with heavy Higgs => new light scalar must exist A. Bay Beijng October 2005 43

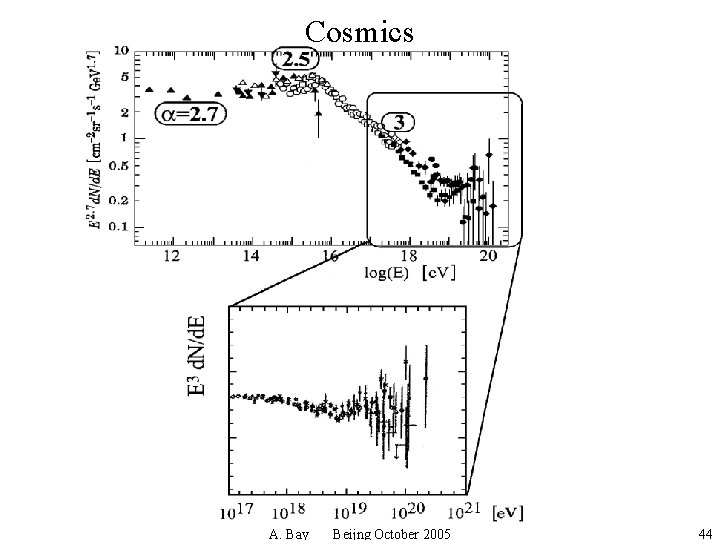
Cosmics A. Bay Beijng October 2005 44

masses & mixings In the SM, CPV is related to the mass generation mechanism for the fermions. The fermionic system is far from being understood. Is there any "periodicity" in the mass spectrum? Similar question for the mixing matrices. A. Bay Beijng October 2005 45

Lepton-quark mass relations first (? ) discussed by A. Buras, J. Ellis, M. K. Gaillard and D. V. Nanopoulos, Nucl. Phys. B 135 (1978) 66 Any horizontal symmetry ? ? H (CKM) (NMS) V CPV, n mix. , baryogenesis: hep-ph/0108216 v 2 * Neutrino mix and CPV in B: hep-ph/0205111 v 2 Bs-Bs mixing in SO(10) SUSY GUT linked to nm nt mix. hep-ph/0312145 A. Bay Beijng October 2005 46

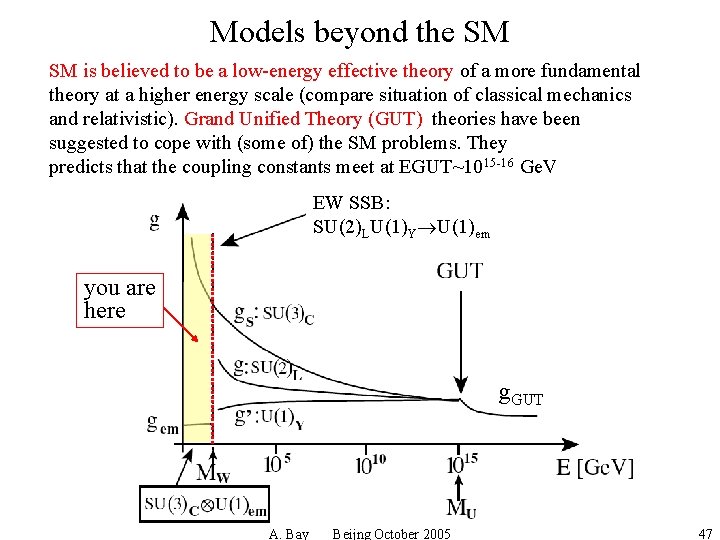
Models beyond the SM SM is believed to be a low-energy effective theory of a more fundamental theory at a higher energy scale (compare situation of classical mechanics and relativistic). Grand Unified Theory (GUT) theories have been suggested to cope with (some of) the SM problems. They predicts that the coupling constants meet at EGUT~1015 -16 Ge. V EW SSB: SU(2)LU(1)Y U(1)em you are here g. GUT A. Bay Beijng October 2005 47

SUSY The Minimal Supersymmetric extension of the SM (MSSM) with gauge coupling unification at EGUT = 1016 Ge. V predicts the EW mixing parameter: sin 2 q. W= 0. 2336 ± 0. 0017 to be compared with the experiemental value particle superparticle sin 2 q. W= 0. 23120± 0. 00015. The model predicts the existence of new particles. A. Bay Beijng October 2005 48

How to detect New Physics ? Direct searches: search for new particles, for instance the supersymmetric partners of particles. New phenomenologies, indirect effects: ex. 1: proton decay ex. 2: EDM measurement ex. 3: Hadronic flavour physics very powerful (think to KM prediction of 3 quark families). It can in principle probe very high energies (think to the Z was "seen" in low energy experiments, as an interference effect). Problem: very often complex underlying theory, with large errors. A. Bay Beijng October 2005 49

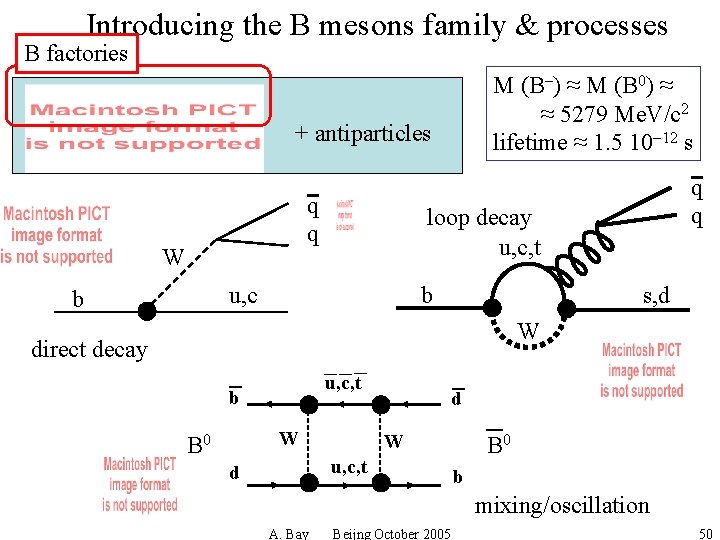
Introducing the B mesons family & processes B factories M (B-) ≈ M (B 0) ≈ ≈ 5279 Me. V/c 2 lifetime ≈ 1. 5 10 -12 s + antiparticles q q W loop decay u, c, t b u, c b q q s, d W direct decay u, c, t b W B 0 d W u, c, t d B 0 b mixing/oscillation A. Bay Beijng October 2005 50

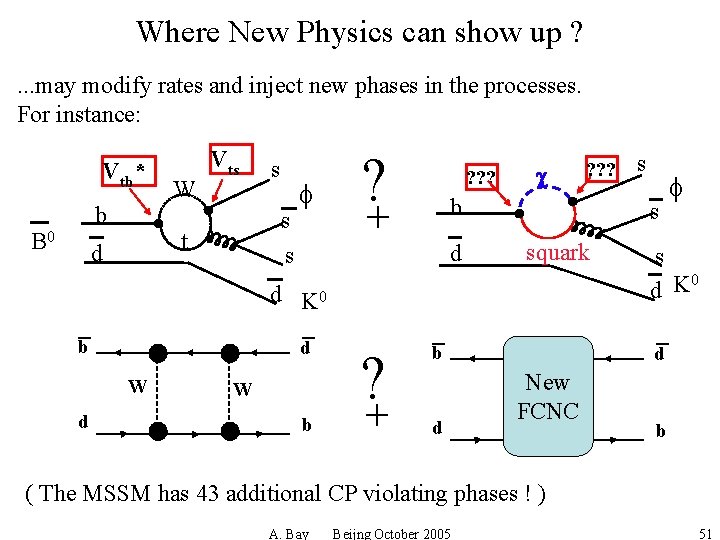
Where New Physics can show up ? . . . may modify rates and inject new phases in the processes. For instance: Vtb* b B 0 W Vts s s t d s f ? ? ? ? c b + d d W b ? + squark b d s s d K 0 b ? ? ? f s 0 d K d New FCNC b ( The MSSM has 43 additional CP violating phases ! ) A. Bay Beijng October 2005 51