Summarizing Itemset Patterns A ProfileBased Approach Xifeng Yan

Summarizing Itemset Patterns: A Profile-Based Approach Xifeng Yan, Hong Cheng, Jiawei Han, Dong Xin ACM KDD 05’ Advisor：Jia-Ling Koh Speaker：Yu-Jiun Liu 2006/01/06 1

Introduction Ⅰ o o o Closed frequent pattern no super-pattern with the same support. Maximal no frequent super-pattern. Top-K V. S. K representatives 2

Introduction Ⅱ o The format of these representatives. o How to find these representatives? o The measure of their quality. 3

Definition o Bernoulli Distribution Vector o Pattern Profile 4

Equations 1. The relative frequency of item οi in D’. 2. Estimated Support 5

Pattern Profile Example o o Both of the above datasets can be summarized by <abcd>, but the quality is better for D 1. p(a) = (50+1000)/(50+1000) = 0. 91 Mabc = <[0. 91, 0. 96, 1], abcd, 0. 87> M = <[0. 91, 0. 96, 1, 1], abcd, 1> o 6

Pattern Summarization o o o First, construct a special profile for each pattern that only contains that pattern itself. Use the Kullback-Leibler divergence to merge similar patterns. KL-divergence 7

Hierarchical Agglomerative Clustering 8

K-means Clustering 9

Optimization Heuristics o Closed Itemset vs. Frequent Itemsets • o Given patterns α and β, if supports are equal, then and their Approximate Profiles • Using the following two equations to instead of original profile updating. for Algorithm 1 for Algorithm 2 10

Quality Evaluation o Definition (Restoration Error) o T is a testing pattern set. o T’ is the collection of the itemsets generated by the master patterns in profiles and. 11

Quality Evaluation o o o J tests “frequent patterns”, some of which may be estimated as “infrequent”. Jc tests “estimated frequent patterns”, some of which are actually “infrequent”. Therefore J and Jc are complementary to each other. 12

Quality Evaluation o Lemma • For any frequent itemset π, there must exist a profile Mk such that , where ψk is the master itemset of Mk. 13

Optimal Number of Profiles o o How to determine K? M = (p, ψ , ρ) • o o Ex: require for any i such that p~q α~β Dα~Dβ~Dα∪Dβ Checking the derivative of the quality over K • , If J increase suddenly from K* to K* - 1, K* is likely to be a good choice. 14

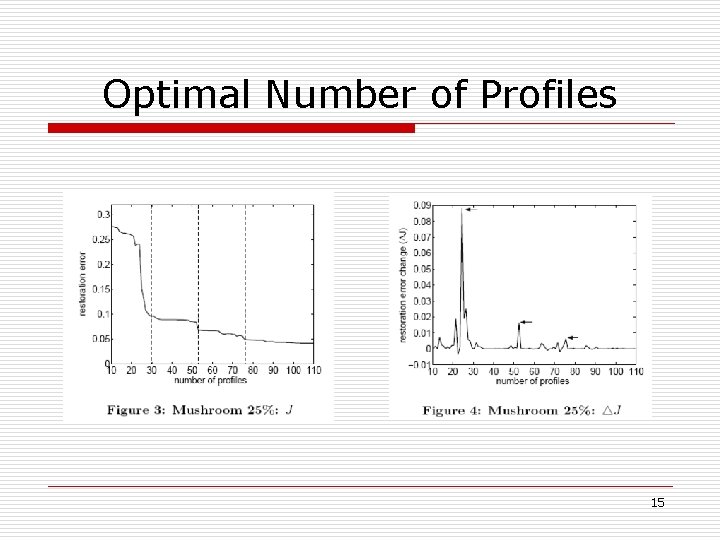
Optimal Number of Profiles 15

Experiment o o o Three real datasets and a series of synthetic datasets. Language: Visual C++ CPU: Intel 3. 2 GHz Memory: 1 GB OS: Windows XP 16

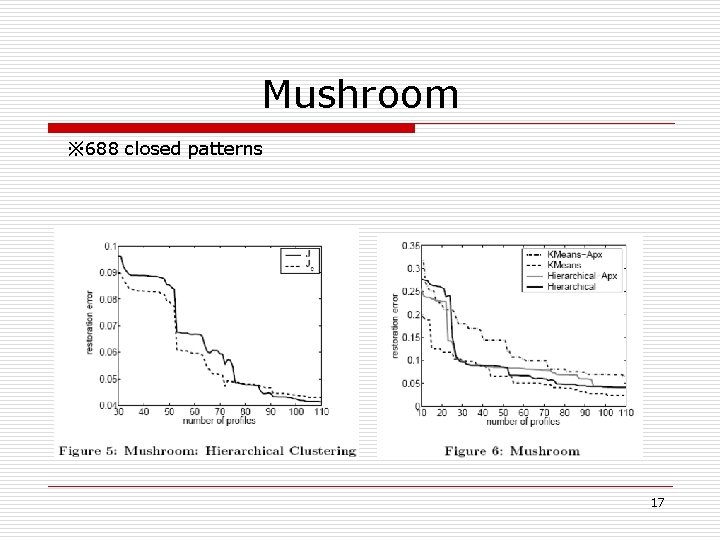
Mushroom ※ 688 closed patterns 17

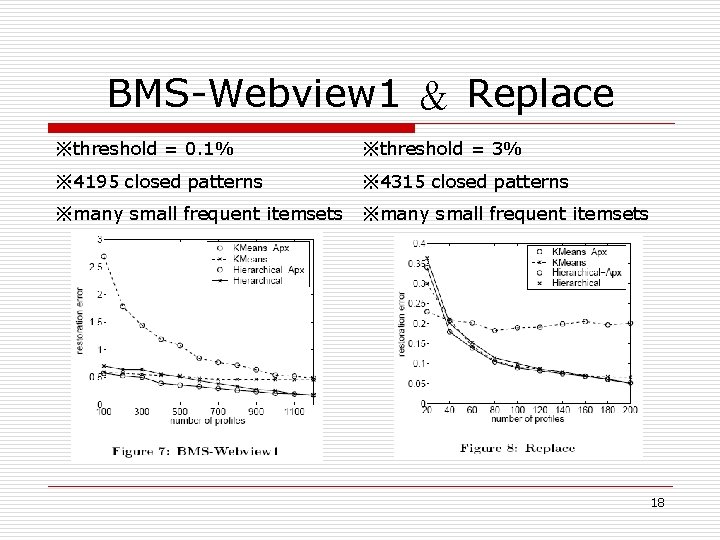
BMS-Webview 1 ＆ Replace ※threshold = 0. 1% ※threshold = 3% ※ 4195 closed patterns ※ 4315 closed patterns ※many small frequent itemsets 18

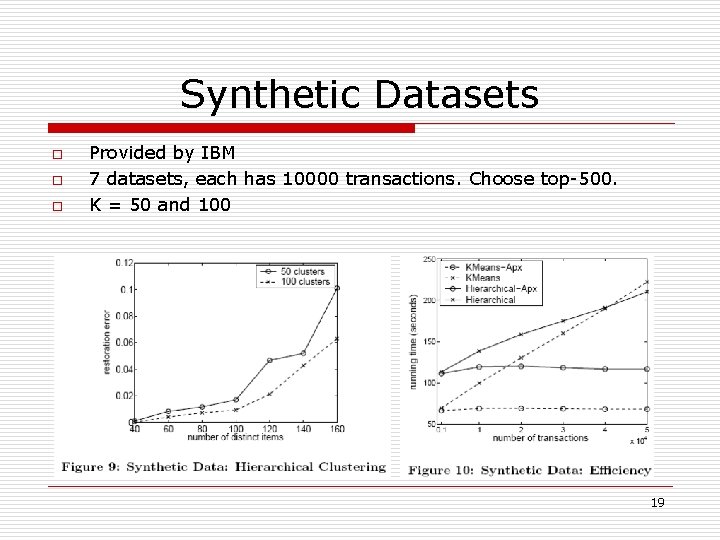
Synthetic Datasets o o o Provided by IBM 7 datasets, each has 10000 transactions. Choose top-500. K = 50 and 100 19