Sum Difference Product and Quotient of Functions Given

Example 1 Adding, Subtracting, Multiplying, and Dividing Functions

Composition of Functions The composition of f and g, denoted f ∘ g, is

Example 3 Combining Functions Given the functions defined by f(x) = x – 7

Example 4 Finding Function Values from a Graph For the functions f and g

• Previously, we defined a function as a set of ordered pairs (x,

• Now suppose we create a new function in which the values of

• A necessary condition for a function f to have an inverse function

Using the Horizontal Line Test Consider a function defined by a set of points

1 Identifying a One-to-One Function For each function, determine if the function is one-to

Definition of an Inverse Function If f is a one-to-one function represented by ordered

Inverse Function Property If f is a one-to-one function, then g is the inverse

2 Composing a Function with Its Inverse Show that the functions are inverses.

Finding an Equation of an Inverse of a Function For a one-to-one function defined

3 Finding an Equation of the Inverse of a Function Find the inverse.

3 Finding an Equation of the Inverse of a Function

4 Finding an Equation of the Inverse of a Function Find the inverse of

4 Finding an Equation of the Inverse of a Function

5 Finding the Equation of an Inverse of a Function with a Restricted Domain

Slides: 34

Download presentation

Sum, Difference, Product, and Quotient of Functions Given two functions f and g, the functions are defined as

Example 1 Adding, Subtracting, Multiplying, and Dividing Functions

Composition of Functions The composition of f and g, denoted f ∘ g, is defined by the rule provided that g(x) is in the domain of f. Note: f ∘ g is also read as “f compose g. ”

Example 2 Composing Functions

Example 3 Combining Functions Given the functions defined by f(x) = x – 7 and h(x) = 2 x 3, find the function values, if possible.

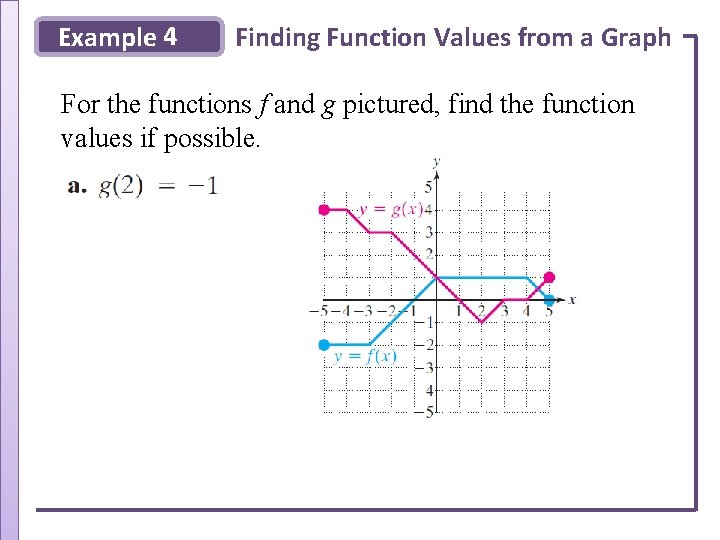
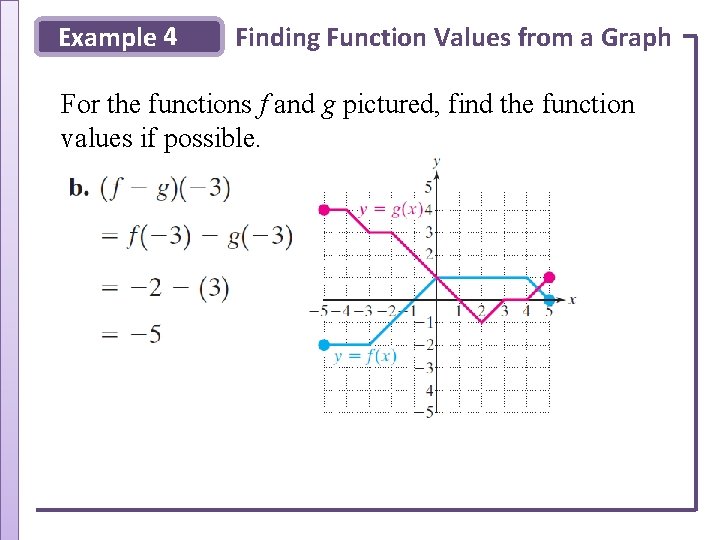
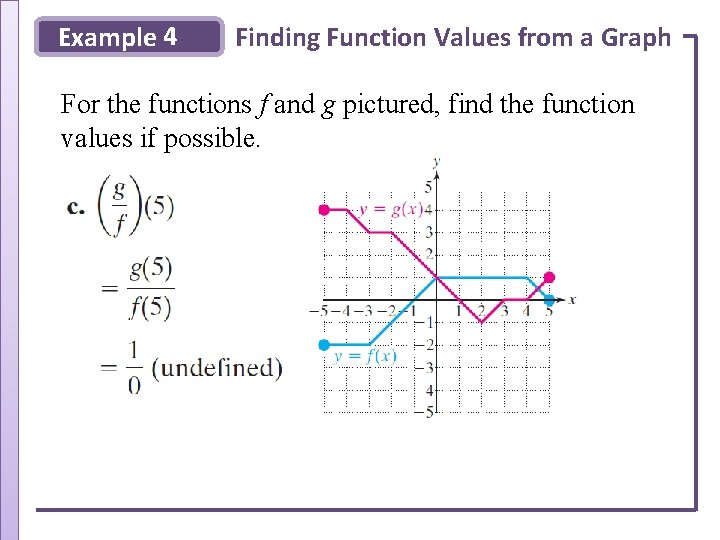
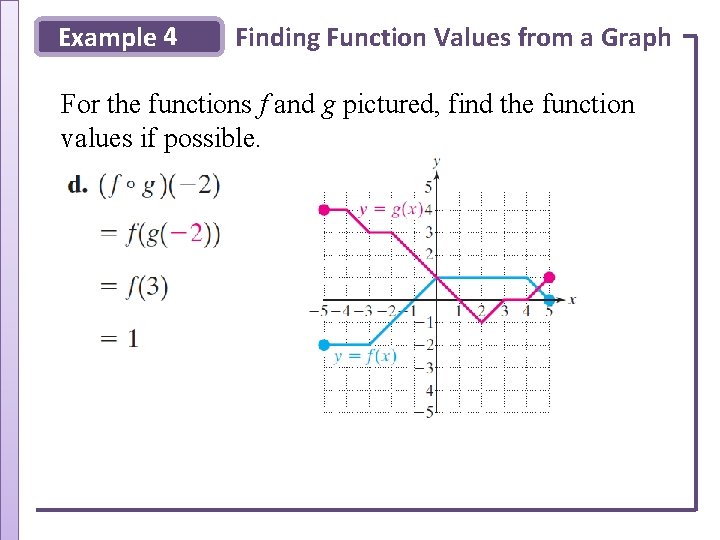
Example 4 Finding Function Values from a Graph For the functions f and g pictured, find the function values if possible.

• Previously, we defined a function as a set of ordered pairs (x, y) such that for every element x in the domain, there corresponds exactly one element y in the range. • For example, the function f relates the weight of a package of deli meat, x, to its cost, y. • That is, 1 lb of meat sells for $4, 2. 5 lb sells for $10, and 4 lb sells for $16.

• Now suppose we create a new function in which the values of x and y are interchanged. • The new function, called the inverse of f, denoted f − 1, relates the price of meat, x, to its weight, y. • Notice that interchanging the x- and y-values has the following outcome. • The domain of f is the same as the range of f − 1, and the range of f is the domain of f − 1.

• A necessary condition for a function f to have an inverse function is that no two ordered pairs in f have different x-coordinates and the same y-coordinate. • A function that satisfies this condition is called a one-to-one function.

Using the Horizontal Line Test Consider a function defined by a set of points (x, y) in a rectangular coordinate system. Then y is a one-to -one function of x if no horizontal line intersects the graph in more than one point.

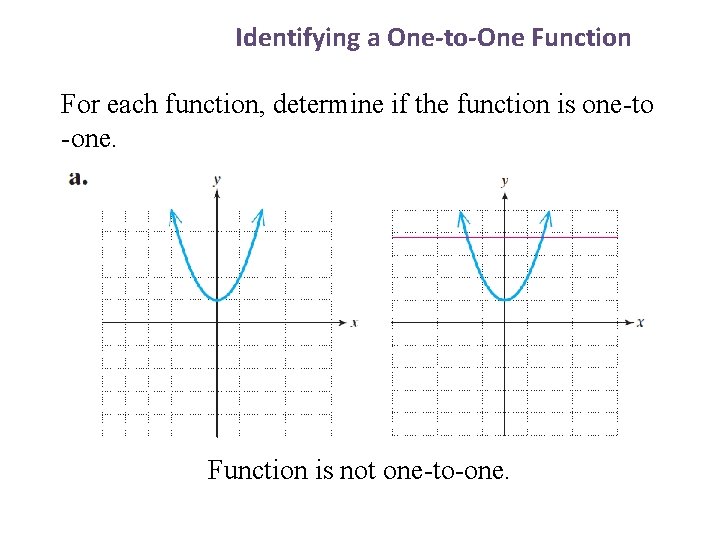
1 Identifying a One-to-One Function For each function, determine if the function is one-to -one. Function is not one-to-one.

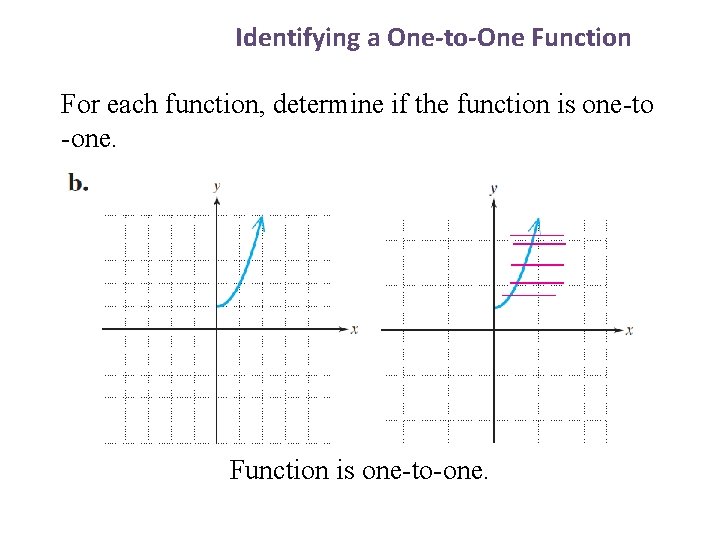
1 Identifying a One-to-One Function For each function, determine if the function is one-to -one. Function is one-to-one.

Definition of an Inverse Function If f is a one-to-one function represented by ordered pairs of the form (x, y), then the inverse function, denoted by f− 1, is the set of ordered pairs given by (y, x).

Inverse Function Property If f is a one-to-one function, then g is the inverse of f if and only if and

2 Composing a Function with Its Inverse Show that the functions are inverses.

Finding an Equation of an Inverse of a Function For a one-to-one function defined by y = f ( x ), the equation of the inverse can be found as follows: Step 1 Replace f ( x ) by y. Step 2 Interchange x and y. Step 3 Solve for y. Step 4 Replace y by f − 1 ( x ).

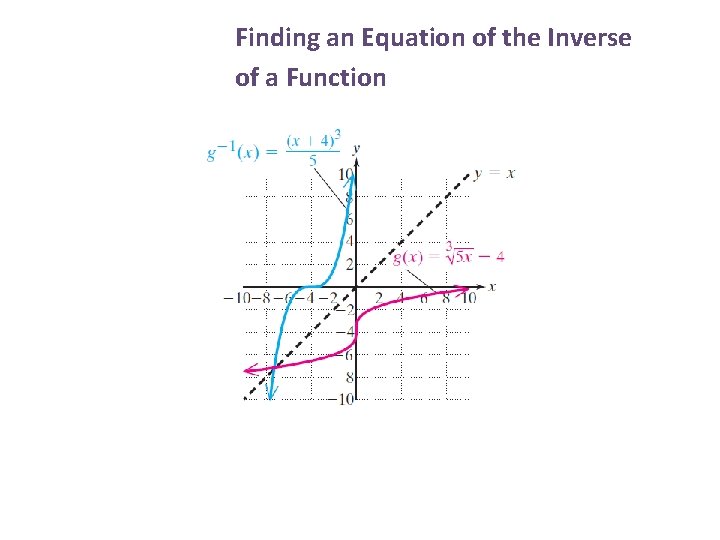
3 Finding an Equation of the Inverse of a Function Find the inverse.

3 Finding an Equation of the Inverse of a Function

4 Finding an Equation of the Inverse of a Function Find the inverse of the one-to-one function.

4 Finding an Equation of the Inverse of a Function

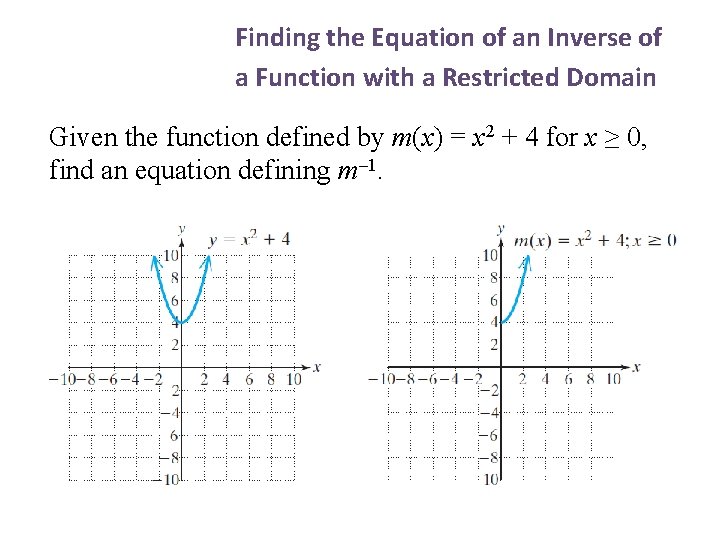
5 Finding the Equation of an Inverse of a Function with a Restricted Domain Given the function defined by m(x) = x 2 + 4 for x ≥ 0, find an equation defining m– 1.