SUKU BANYAK Oleh Hayani Hamudi S Pd Standar

SUKU BANYAK Oleh : Hayani Hamudi, S. Pd

Standar Kompetensi 4. Menggunakan aturan Suku banyak dalam Penyelesaian Masalah Kompetensi Dasar 4. 1 Menggunakan algoritma pembagian suku banyak untuk menentukan hasil bagi dan sisa pembagian 4. 2 Menggunakan Teorema sisa dan teorema faktor dalam memecahkan masalah

Tujuan Pembelajaran ♥ Siswa dapat menggunakan algoritma Pembagian Suku banyak untuk menentukan hasil bagi dan sisa pembagian ♥ Siswa dapat menggunakan Teorema sisa dan teorema faktor dalam Pemecahan masalah

Aspek Penyajian q Peng. Suku banyak, nilai suku banyak, dan operasi antarsukubanya q Pembagian suku banyak q Teorema sisa q Teorema Faktor

Pengertian Suku Banyak Nilai Suku Banyak Operasi Antar Suku Banyak

Pengertian Suku Banyak Suku banyak adalah suatu bentuk aljabar yang memiliki Bentuk umum anxn + an-1 x n-1 + an-2 x n-2 + … + a 2 x 2 + a 1 x 1 + a 0 ao, a 1, an-2, an bil. real an ≠ 0 ao, a 1, an-2, an koefisien dan ao suku tetap Suku banyak terdiri dari 2 yaitu yang mempunyai satu variabel ( univariabel) dan suku banyak yang lebih dari satu variabel ( multivariabel) Contoh: 3 x 5 + 6 x 4 - 2 x 2 - 4 x + 7 Suku banyak diatas merupakan suku banyak berderajat 5 dimana, Koef dari X 5 adalah 3 Koef dari x 4 adalah 6 Koef dari x 3 adalah 0 koef dari x 2 adalah -2 Koef dari x adalah -4 Suku tetapnya adalah 7

Nilai Suku Banyak Suku banyak dapat dinyatakan dalam fungsi berikut f(x) = anxn + an-1 x n-1 + an-2 x n-2 + … + a 2 x 2 + a 1 x 1 + a 0 Kadang dinyatakan dengan P(x) atau S(x) Nilai suku banyak dapat dicari dengan 2 metode, yaitu ♥ Metode Substitusi/ Langsung ♥ Metode bagan / Skema

Metode Substitusi Jika diketahui polinom f(x) = anxn + an-1 x n-1 + … + a 2 x 2 + a 1 x 1 + a 0 Untuk x = P, maka f(x) = anpn + an-1 pn-1 + … + a 2 p 2 + a 1 p 1 + a 0 Disebut nilai suku banyak Contoh Tent. Nilai suku banyak Jika diketahui polinom f(x) = x 3 + 3 x 2 - x + 5 untuk nilai x = 2 Penye; Untuk x = 2, diperoleh f(2) = (2)3 + 3(2)2 - 2 + 5 f(2) = 8 + 3. 4 - 2 + 5 = 8 + 12 - 5 = 13 Jadi, nilai f(x) untuk x = 2 adalah f(2) = 13

Contoh Dik. Suku banyak dengan 2 variabel yaitu x dan y. Hitung nilai suku banyak f(x, y) = x 3 y+ 3 x 2 y 2 - 2 x + 4 y + 2 untuk f(2, 1) Penye; Untuk x = 2 dan y = 1 diperoleh f(x, y) = x 3 y+ 3 x 2 y 2 - 2 x + 4 y + 2 f(2, 1) = (2)3. 1+ 3(2)2(1)2 – 2. (2) + 4. (1) + 2 f(2, 1) = 8. 1 + 3. 4. 2 - 5 + 4 + 2 f(2, 1) = 8 + 24 - 5 + 4 + 2 = 33 Jadi, nilai f(x) untuk x = 2 dan y = 1 adalah f(2, 1) = 33

Metode Bagan / Skema Misal f(x) = ax 3 + bx 2 + cx+ d, untuk x = p berlaku f(p) = ap 3 + bp 2 + cp + d Bentuk ini dapat diubah menjadi f(p) = (ap 2 + bp + c)p + d f(p) = ((ap + b)p + c)p + d Jadi, f(p) = ap 3 + bp 2 + cp + d dapat diperoleh dengan cara: ♥ Kalikan a dengan p lalu tambah b, hasilnya (ap+b) ♥ Kalikan (ap+b) dengan p lalu tambah c, hasilnya (ap+b)p + c atau ap 2 + bp + c ♥ Kalikan ap 2 + bp + c dengan p lalu tambah d hasilnya (ap 2 +bp +c)p +d = ap 3 +bp 2 +cp + d

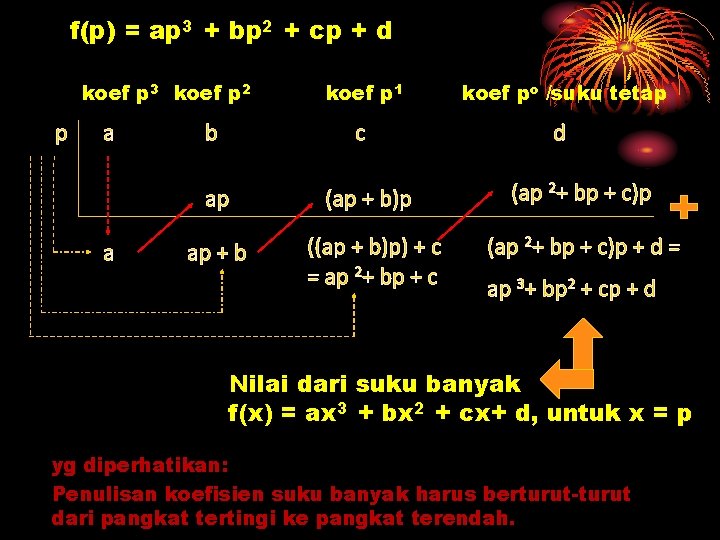
f(p) = ap 3 + bp 2 + cp + d koef p 3 koef p 2 p a a b koef p 1 koef po /suku tetap c d ap (ap + b)p (ap 2+ bp + c)p ap + b ((ap + b)p) + c = ap 2+ bp + c (ap 2+ bp + c)p + d = ap 3+ bp 2 + cp + d Nilai dari suku banyak f(x) = ax 3 + bx 2 + cx+ d, untuk x = p yg diperhatikan: Penulisan koefisien suku banyak harus berturut-turut dari pangkat tertingi ke pangkat terendah.

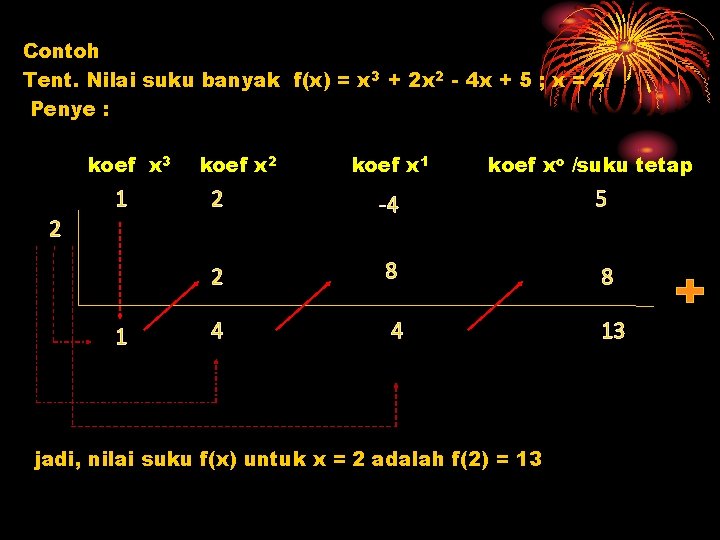
Contoh Tent. Nilai suku banyak f(x) = x 3 + 2 x 2 - 4 x + 5 ; x = 2 Penye : koef x 3 1 koef x 2 koef xo /suku tetap 2 -4 5 2 8 8 4 4 13 2 1 koef x 1 jadi, nilai suku f(x) untuk x = 2 adalah f(2) = 13

Contoh Tent. Nilai suku banyak f(x) = 2 x 4 + x 2 + 3 x + 2 ; x = 3 substitusi dan metode bagan !!! Penye : Metode substitusi Untuk x = 3, diperoleh f(3) = 2(3)4 + (3)2 + 3(3) + 2 f(2) = 2. (81) + 9 +9 + 2 = 162 + 9 + 2 = 182 Jadi, nilai f(x) untuk x = 3 adalah f(3) = 182 Metode Bagan/ Skema 3 koef x 4 2 2 koef x 3 0 koef x 2 1 dengan metode koef x 1 koef po /suku tetap 3 2 6 18 57 180 6 19 60 182 Jadi, nilai f(x) untuk x = 3 adalah f(3) = 182

Operasi Antarsukubanyak A. Penjumlahan dan Pengurangan Penjumlahan atau pengurangan suku banyak f(x) dengan suku banyak g(x) menjumlahkan atau mengurangkan suku – suku yang sejenis Misal ☻ 2 x 2 sejenis dengan 3 x 2 sehingga 2 x 2 + 3 x 2 = (2+3)x 2 = 5 x 2 ☻ 3 y 4 sejenis dengan y 4 sehingga 3 y 4 – y 4 = (3 -1)y 4 = 2 y 4 ☻ 2 y 3 tidak sejenis dengan 2 x 3 sehingga 2 y 3+ 2 x 3 = 2 y 3+ 2 x 3 ☻ 5 x 3 tidak sejenis dengan 2 x 2 sehingga 5 x 3 - 2 x 2 = 5 x 3 - 2 x 2 Misal f(x) dan g(x) masing merupakan suku banyak berderajat m dan n maka f(x) ± g(x) adalah suku banyak berderajat m atau n

Contoh : Dik. f(x) = 3 x 2 + 4 x + 1 dan g(x) = 2 x 4 + 3 x 2 – 6 x + 4 Tent. f(x) + g(x) dan f(x) – g(x) serta derajatnya f(x) + g(x) = (3 x 2 + 4 x + 1) + (2 x 4 + 3 x 2 – 6 x + 4) f(x) + g(x) = (0 + 2 x 4)+ (3 x 2 + 3 x 2) +(4 x – 6 x) + (1+4) f(x) + g(x) = 2 x 4 + 6 x 2 + (– 2 x) + 5 f(x) + g(x) = 2 x 4 + 6 x 2 – 2 x + 5 Jadi, f(x) + g(x) = 2 x 4 + 6 x 2 – 2 x + 5 dan f(x) + g(x) berderajat 4 f(x) - g(x) = (3 x 2 + 4 x + 1) - (2 x 4 + 3 x 2 – 5 x + 4) f(x) - g(x) = (0 -2 x 4)+ (3 x 2 - 3 x 2) +(4 x – (-6 x) + (1 -4) f(x) - g(x) = (-2 x 4)+ 0 + 10 x + (-3) f(x) - g(x) = -2 x 4 + 10 x - 3 Jadi, f(x) - g(x) = -2 x 4 + 10 x - 3 dan f(x) - g(x) berderajat 4

Perkalian Antar. Suku Banyak Perkalian suku banyak f(x) dengan g(x) ü Mengalikan suku-suku dari kedua suku banyak. ü Dalam mengalikan suku-suku dari kedua suku digunakan sifat distribusi perkalian ( distribusi perkalian terhadap penjumlahan maupun distribusi perkalian terhadap pengurangan , kemudian baru dihitung jumlahnya. Misalkan f(x) dan g(x) masing-masing merupakan suku banyak berderajat m atau n maka: f(x). g(x) adalah suku banyak berderajat m+n Misalkan f(x) = 3 x 2 + 4 x + 1 adalah suku banyak berderajat 2 g(x) = 2 x 4 + 3 x 2 – 6 x + 4 adalah suku banyak berderajat 4 Maka hasil perkalian f(x) dengan g(x) berderajat 2+4 = 6

Contoh Tent. Hasil dan derajat perkalian dari 1. 2 x 2 - 4 x + 5 dengan x 2 + 4 2. X - 2 dengan (2 x + 1)2 Penyelesaian : (2 x 2 – 4 x + 5)(x 2 + 4) = 2 x 2(x 2 + 4) -4 x(x 2 + 4) + 5(x 2 + 4) = 2 x 4 + 8 x 2 – 4 x 3 – 16 x + 5 x 2 + 20 = 2 x 4 – 4 x 3 + 8 x 2 + 5 x 2 – 16 x + 20 = 2 x 4 – 4 x 3 + 13 x 2 – 16 x + 20 Hasilnya suku banyak berderajat 4 atau 2 + 2 = 4 Ingat!!! am x an = a m+n (x - 2)(2 x + 1)2 = (x – 2)(4 x 2 + 4 x + 1) = x (4 x 2 + 4 x + 1) – 2(4 x 2 + 4 x + 1) = 4 x 3 + 4 x 2 + x – 8 x 2 – 8 x – 2 = 4 x 3 + 4 x 2 – 8 x 2 + x – 8 x – 2 = 4 x 3 – 4 x 2 – 7 x – 2 Hasilnya suku banyak berderajat 3 atau 1 + 2 = 3

Kesamaan Suku Banyak Misalkan f(x) dan g(x) adalah dua buah suku banyak f(x) = anxn + an-1 x n-1 + … + a 2 x 2 + a 1 x 1 + a 0 g(x) = bnxn + bn-1 xn-1 + … + b 2 x 2 + b 1 x 1 + b 0 f(x) ≡ g(x) jika dan hanya jika an = bn; an-1 = bn-1; … ; a 2 = b 2; a 1 = b 1; a 0 = b 0 Contoh Tentukan nilai a, b, c, dan d, jika X 4 - 8 x 3 – 15 x – 20 = x 4 + ax 3 + (a+b)x 2 + (26 -c)x + d Penyelesaian

X 4 - 8 x 3 + 15 x – 20 = x 4 + ax 3 + (a+b)x 2 + (26 -c)x + d Misal f(x) = X 4 - 8 x 3 + 15 x – 20 Misal g(x) = x 4 + ax 3 + (a+b)x 2 + (26 -c)x + d Koefisien x 4 Koefisien x 3 Koefisien x 2 Koefisien x 0 f(x) = g(x) 1=1 -8 = a 0=a+b 15 = 2 b – c -20 = d pers 5 disubs. ke pers 3, diperoleh: 15 = 2 b - c 15 = 2(8) - c 15 = 16 - c C = 16 – 15 = 1 pers. 2 pers. 3 pers. 4 pers 1 disubs. ke pers 2, Diperoleh: 0=a+b 0 = (-8) + b 8 = b pers. 5 dari uraian diatas, diperoleh: a = -8 c=1 b= 8 d = -20

Pembagian suku Banyak Hubungan antara yang dibagi, Pembagi, Hasil Bagi, dan Sisa Pembagian Cara pembagian suku banyak * Cara Biasa/ Langsung * Cara Skema/ Horner Pembagian suku banyak dengan; * Pembagi berbentuk linear; ( x – k) dan (ax – b) * Pembagi berbentuk kuadrat ( ax 2 + bx + c)

2 2 5 4 1

Hub. Antara yang dibagi, pembagi, hasil bagi, dan sisa Pembagian. perhatikan pembagian bersusun dibawah 3 4 Dari (i) terlihat bahwa 7 dibagi 2 2 dengan 2 memberikan hasil 3 7 8 dengan sisa pembagian 1 6 8 Dari (ii) terlihat bahwa 8 dibagi 1 0 dengan 2 memberikan hasil 4 (i) ( ii ) dengan sisa pembagian 0 (i) 7=2 x 3+1 ( ii ) 8 = 4 x 4 + 0 Dengan demikian dapat dirumuskan sebagai berikut: Yang dibagi = pembagi x hasil bagi + sisa pembagian

Pembagian suku Banyak berbentuk linear; (x – k) dan (ax + b) Cara yang digunakan untuk membagi suku banyak dengan pembagi berbentuk linear dikenal dengan cara biasa dan cara horner Pembagi suku banyak dengan (x – k) Hub. Antara yang dibagi, pembagi, hasil bagi, dan sisa Hub. Antarayang dibagi, pembagi, hasilbagi, dan dansisa sis pembagian adalah Hub. Antara dibagi, f(x) = ( x – k ). H(x) + S Dimana, f(x) = fungsi yang dibagi ( x – k ) = pembagi H(x) = hasil bagi S = sisa pembagian Catatan…. Derajat hasil bagi ditambah derajat pembagi sama dengan derajat yang dibagi

Tent. Hasil bagi, sisa pembagian, dan hub. Yang dibagi, Hasil bagi, pembagi, sisa pembagian berikut: (x 3 – 11 x + 10) : (x – 5 ) Dengan pembagian bersusun/ biasa x 2 + 5 x + 14 x-5 Dari pembagian disamping X 3 – 11 x + 10 diperoleh; X 3 – 5 x 2 Hasil bagi / H(x) : x 2 + 5 x + 14 5 X 2 – 11 x + 10 5 X 2 – 25 x Sisa pembagian/ S : 80 14 x + 10 14 x - 70 80 Sehingga hub; f(x) = ( x – k ). H(x) + S (x 3 – 11 x + 10) = (x – 5 )(x 2 + 5 x + 14) + 80

Cara horner / Skema Secara umum, pembagian suku banyak f(x) oleh ( x – k ) atau ( x + k) dengan cara horner dapat dilakukan dengan kaidah : Jika pembaginya ( x – k ), faktor pengalih terhadap koefisien 2 suku banyak adalah k Jika pembaginya ( x + k ), faktor pengalih terhadap koefisien 2 suku banyak adalah -k ( x 3 – 11 x + 10 ) : ( x – 5 ) , berarti faktor pengalihnya adalah 5 koef x 3 5 1 1 Hasil bagi koef x 2 koef x 1 koef po /suku tetap 5 25 70 5 14 0 koef x 1 -11 10 80 …. . sisa koef po /suku tetap Hasil bagi H(x) = x 2 + 5 x + 14 Sehingga hubungannya: (x 3 – 11 x + 10) = (x – 5 )(x 2 + 5 x + 14) + 80

Tent. Hasil bagi dan sisa pembagian berikut: (x 3 + 6 x 2 + 3 x – 15) : (x + 3 ) Dengan pembagian bersusun/ biasa x+3 x 2 + 3 x - 6 ……. hasil bagi X 3 + 6 x 2 + 3 x - 15 X 3 + 3 x 2 3 X 2 + 3 x - 15 3 X 2 + 9 x -6 x - 15 -6 x - 18 3 … sisa Diperoleh hasil bagi / H(x) = x 2 + 3 x – 6 Sisa pembagian / S = 3

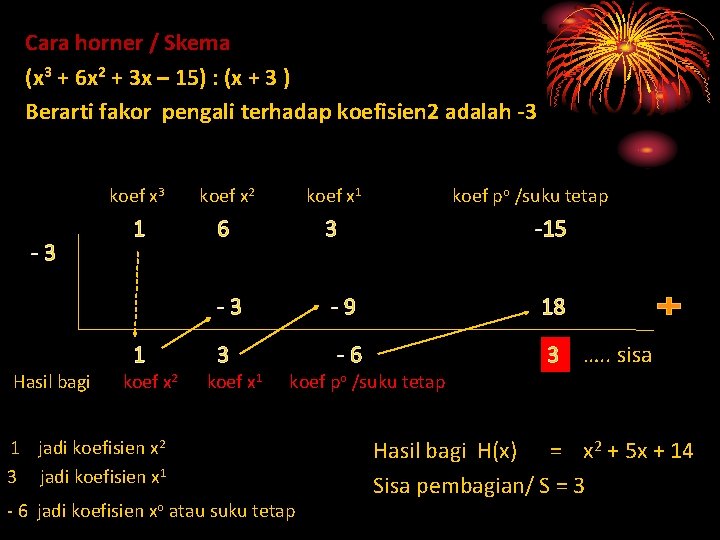
Cara horner / Skema (x 3 + 6 x 2 + 3 x – 15) : (x + 3 ) Berarti fakor pengali terhadap koefisien 2 adalah -3 -3 koef x 2 koef x 1 1 6 3 -15 -3 -9 18 3 -6 3 …. . sisa 1 Hasil bagi koef x 2 koef x 1 koef po /suku tetap 1 jadi koefisien x 2 3 jadi koefisien x 1 - 6 jadi koefisien xo atau suku tetap Hasil bagi H(x) = x 2 + 5 x + 14 Sisa pembagian/ S = 3

Pembagi suku banyak dengan (ax + b) Dengan cara horner Secara umum, pembagian suku banyak f(x) oleh ( ax + b ) atau ( ax b) dengan cara horner dapat dilakukan dengan kaidah : Jika pembaginya ( ax + b ), faktor pengalih terhadap koefisien 2 suku banyak adalah Jika pembaginya ( x + k ), faktor pengalih terhadap koefisien 2 suku banyak adalah -k

Tent. Hasil bagi, sisa pembagian, dan hub. Yang dibagi, Hasil bagi, pembagi, sisa pembagian berikut: (x 3 – 11 x + 10) : (x – 5 ) Dengan pembagian bersusun/ biasa x-5 x 2 + 5 x + 14 X 3 – 11 x + 10 X 3 – 5 x 2 5 X 2 – 11 x + 10 5 X 2 – 25 x 14 x + 10 14 x - 70 80 perhatikan pembagian bersusun dibawah XX 3 3–– 5 x 5 x 2 2 X 3 – 5 x 2

Pembagi suku banyak dengan Pembagi Berbentuk Kuadrat (ax 2 + bx + c untuk a ≠ o) jika suatu suku banyak f(x) dibagi dengan ax 2+bx+c, dengan a≠ 0 (untuk ax 2+bx+c, a≠ 0 yang dapat difaktorkan ataupun yang tidak dapat difaktorkan), hasil bagi dan sisa pembagiannya dapat ditentukan dengan cara pembagian bersusun Hubungannya… f(x) = ( ax 2 + bx + c ). H(x) + (px + g) Derajat yang dibagi > derajat Pembagi > derajat Hasil bagi ≥ derajat Sisa

Tent. Hasil bagi dansisa pembagian suku banyak f(x) = 2 x 3 + 3 x + 6 oleh x 2 + x - 1 f(x) = ( ax 2 + bx + c ). H(x) + (px + g) 2 x 3 + 3 x + 6 = ( x 2 + x - 1 ). H(x) + (px + g) Dengan pembagian bersusun/ biasa 2 x - 1 +x-1 2 X 3 + 3 x + 6 2 X 3 + 2 x 2 – 2 x -X 2 + 5 x + 6 -X 2 – x + 1 6 x + 5 Hasil / H(x) = 2 x – 1 dan Sisa / S = 6 x + 5, seingga: ( 2 x 3+3 x+6 ) = ( x 2+x-1 ). ( 2 x– 1 ) + ( 6 x+5 ) x 2

Dengan menggunakan hubungan… f(x) = ( ax 2 + bx + c ). H(x) + S ingat!! Derajat pembagi + derajat asi bagi = derajat yang dibagi Jadi, meliat derajat yang dibagi 3 dan derajat pembagi 2 maka dapat disimpulkan bawa derajat hasil adala 1, sehingga dimisalkan hasil : ax+b dan sisa : px + q f(x) = ( ax 2 + bx + c ). H(x) + S (2 x 3 + x 2 + 3 x + 6) = ( x 2 + x - 1 ). ( ax+b ) + ( px+q ) (2 x 3 + x 2 + 3 x + 6) = ( ax 3 + bx 2 + ax 2 + bx – ax – b) + ( px+q ) (2 x 3 + x 2 + 3 x + 6) = ( ax 3 + bx 2 + ax 2 + bx – ax + px – b +q ) (2 x 3 + x 2 + 3 x + 6) = ax 3 + (b+a)x 2+ (b-a+p)x + ( q-b ) (2 x 3 + x 2 + 3 x + 6) = ax 3 + (a+b)x 2+ (b-a+p)x + ( q-b ) Ingat!!! Kesamaan Suku Banyak

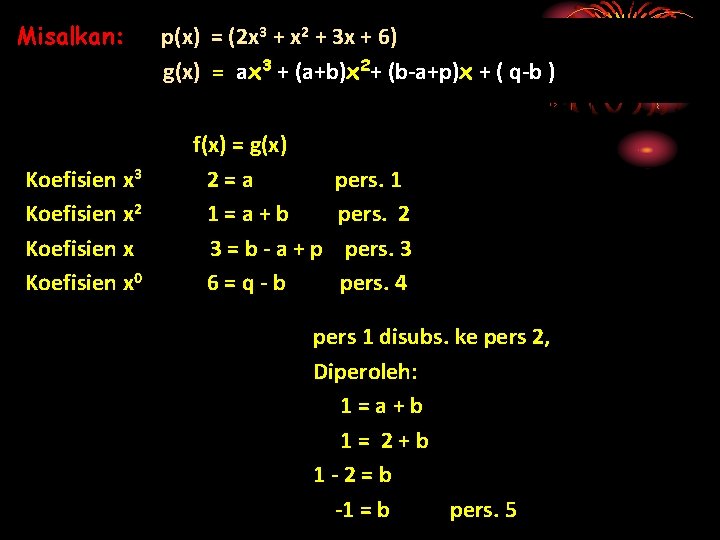
Misalkan: Koefisien x 3 Koefisien x 2 Koefisien x 0 p(x) = (2 x 3 + x 2 + 3 x + 6) g(x) = ax 3 + (a+b)x 2+ (b-a+p)x + ( q-b ) f(x) = g(x) 2=a 1=a+b 3=b-a+p 6=q-b pers. 1 pers. 2 pers. 3 pers. 4 pers 1 disubs. ke pers 2, Diperoleh: 1=a+b 1= 2+b 1 -2=b -1 = b pers. 5

pers 1 & 5 disubs. pers 3, Diperoleh: 3=b–a+p 3 = -1 – 2 + p 3=-3 +p 3+3=p 6=p pers. 6 dari uraian diatas, diperoleh: a=2 p = -6 b = -1 q = 5 pers 5 disubs. ke pers 4, Diperoleh: 6=q-b 6 = q – (-1) 6=q+1 6 -1=q 5= q pers. 7 Sehingga : Hasil / H(x) Sisa / S ax + b = 2 x – 1 px + q = 6 x + 5 (2 x 3 + x 2 + 3 x + 6) = ( x 2 + x - 1 ). ( ax+b ) + ( px+q ) ( 2 x 3+x 2+3 x+6 ) = ( x 2+x-1 ). ( 2 x– 1 ) + ( 6 x+5 )