Suffix trees Trie A tree representing a set

Suffix trees

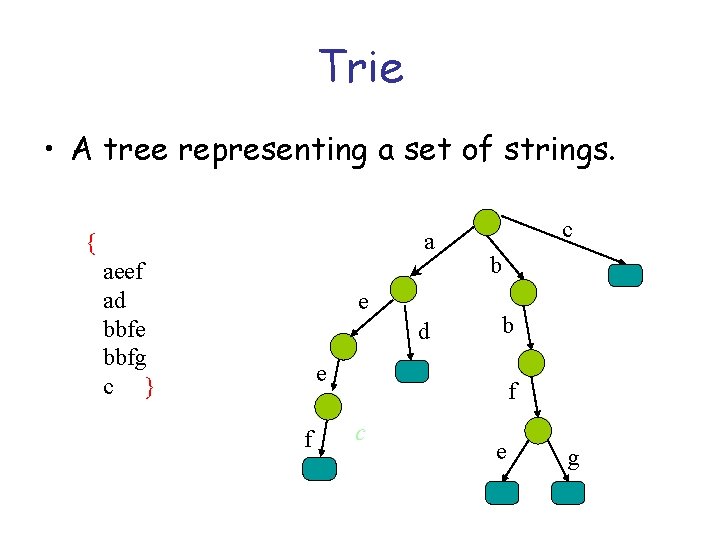
Trie • A tree representing a set of strings. a { aeef ad bbfe bbfg c } e d c b b e f f c e g

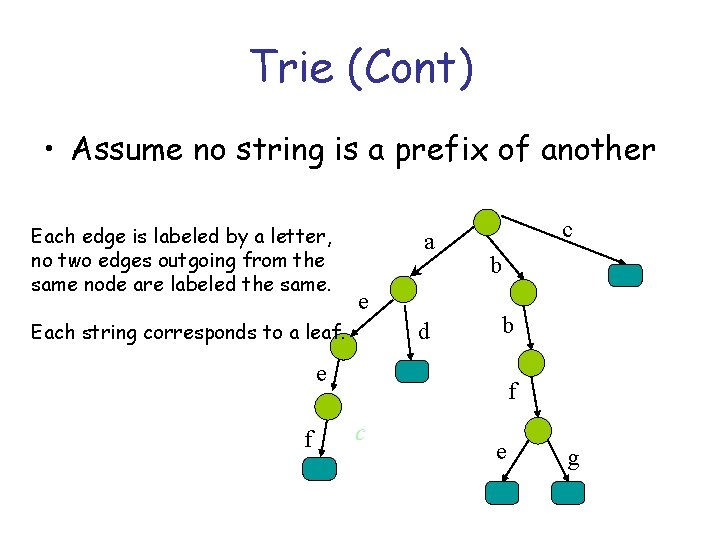
Trie (Cont) • Assume no string is a prefix of another Each edge is labeled by a letter, no two edges outgoing from the same node are labeled the same. a e Each string corresponds to a leaf. d c b b e f f c e g

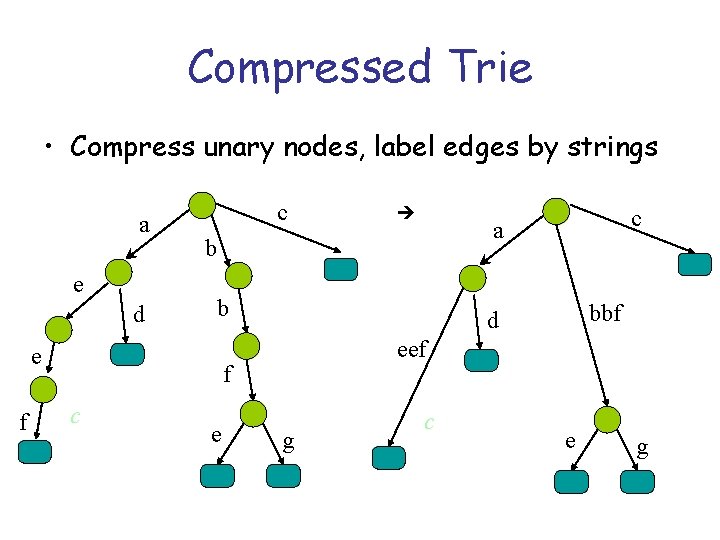
Compressed Trie • Compress unary nodes, label edges by strings a e d c b e bbf d eef f c c a b e f g c e g

Suffix tree Given a string s a suffix tree of s is a compressed trie of all suffixes of s To make these suffixes prefix-free we add a special character, say $, at the end of s

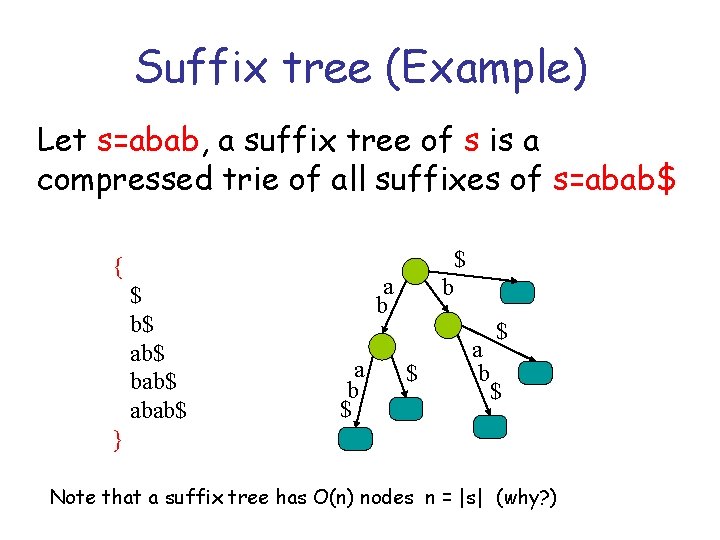
Suffix tree (Example) Let s=abab, a suffix tree of s is a compressed trie of all suffixes of s=abab$ $ { $ b$ ab$ bab$ a b a b $ $ } Note that a suffix tree has O(n) nodes n = |s| (why? )

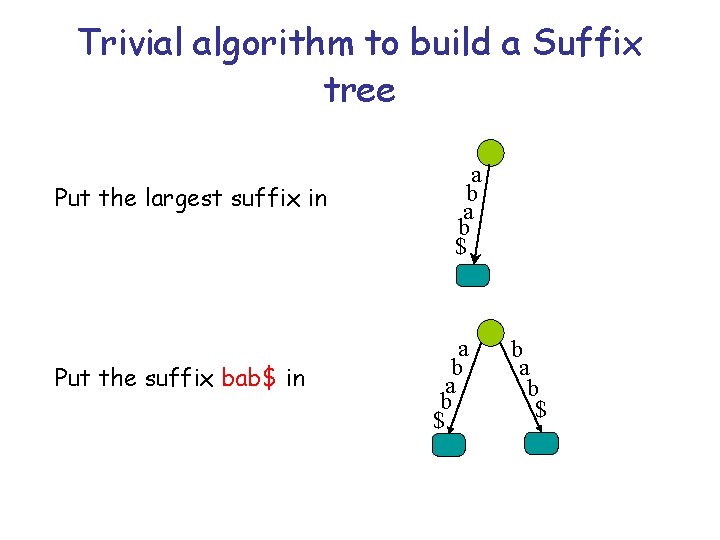
Trivial algorithm to build a Suffix tree Put the largest suffix in Put the suffix bab$ in a b a b $

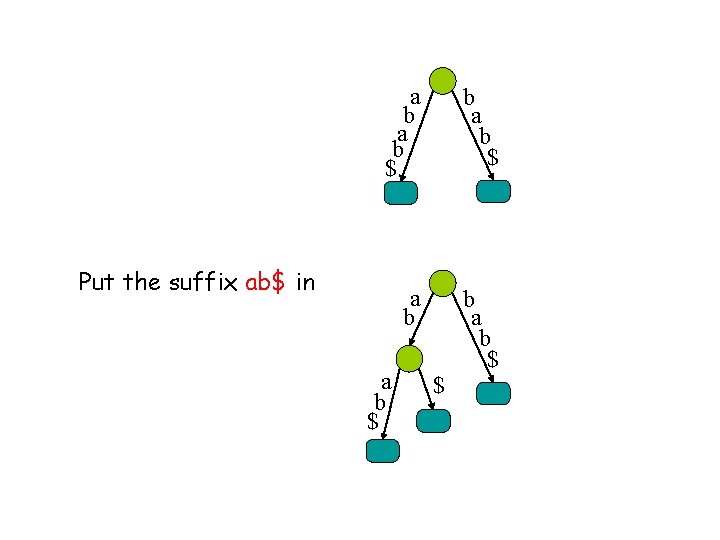
a b $ b a b $ a b b a b $ Put the suffix ab$ in a b $ $

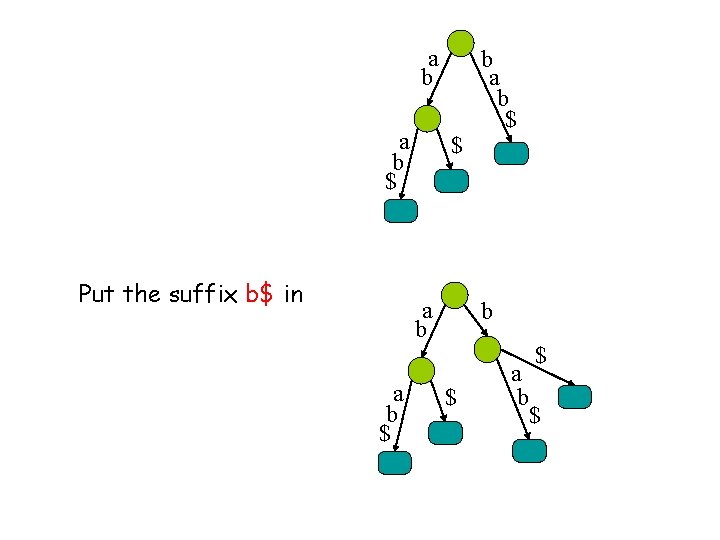
a b $ Put the suffix b$ in $ a b $ b a b $ $

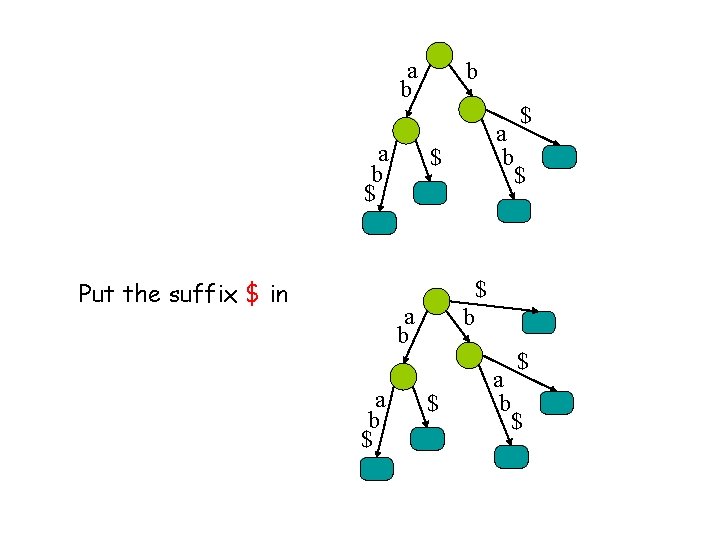
a b $ b a b $ $ Put the suffix $ in a b $ b $ a b $ $

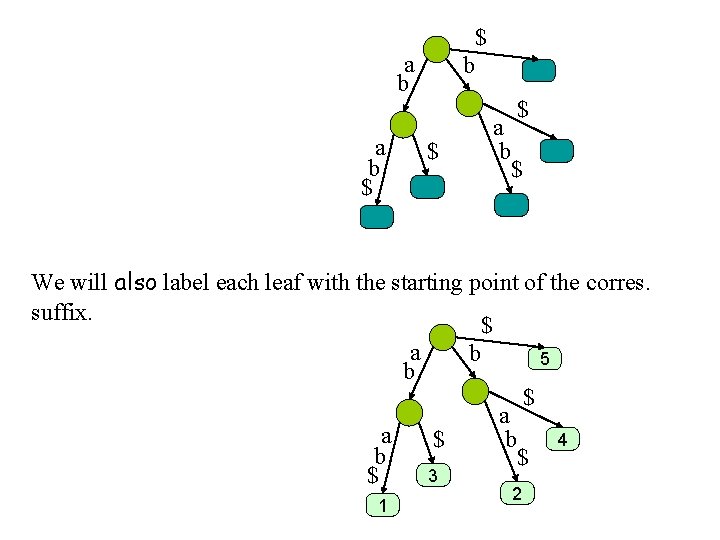
$ a b $ b $ a b $ $ We will also label each leaf with the starting point of the corres. suffix. $ a b 5 b $ a a 4 $ b b $ 3 $ 1 2

Analysis Takes O(n 2) time to build. You can do it in O(n) time But, how come? does it take O(n) space ?

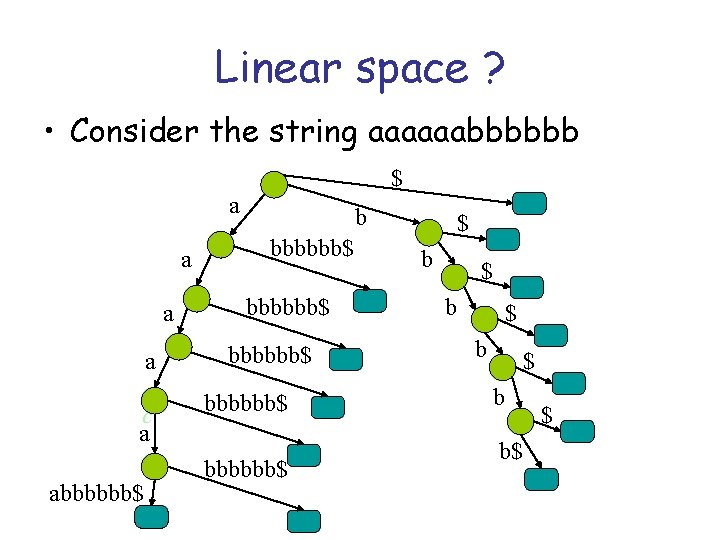
Linear space ? • Consider the string aaaaaabbbbbb $ a a c a abbbbbb$ bbbbbb$ bbbbbb$ $ b $ b b$ $

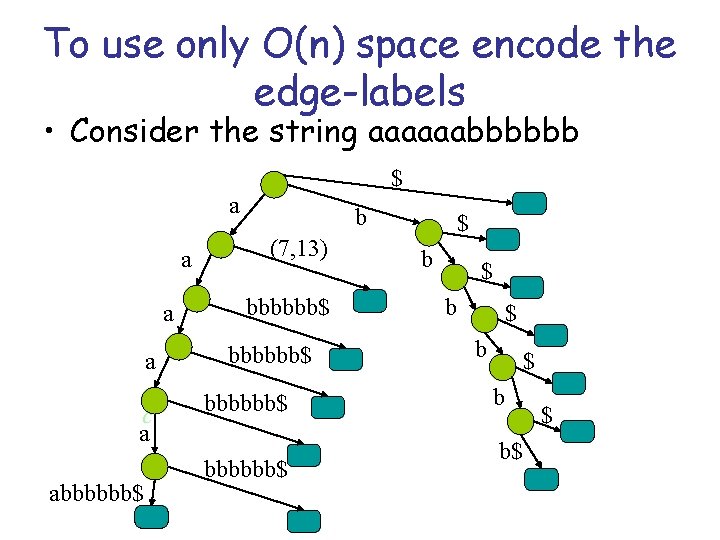
To use only O(n) space encode the edge-labels • Consider the string aaaaaabbbbbb $ a a c a abbbbbb$ b (7, 13) bbbbbb$ $ b $ b b$ $

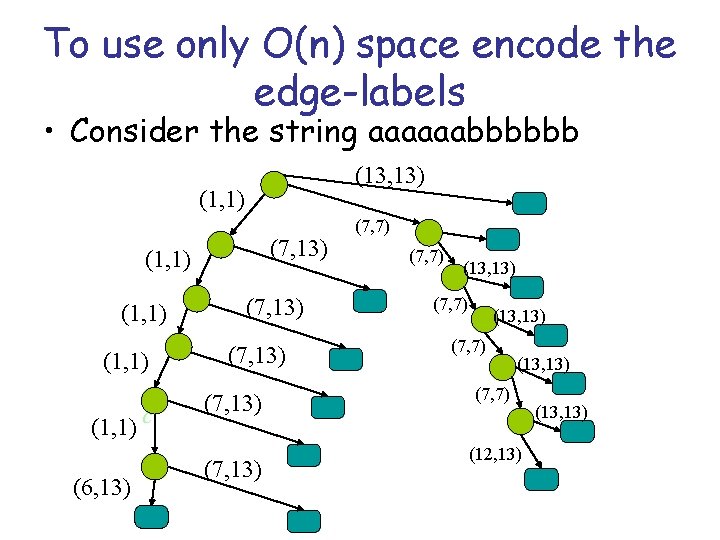
To use only O(n) space encode the edge-labels • Consider the string aaaaaabbbbbb (13, 13) (1, 1) (7, 13) (1, 1) c (6, 13) (7, 13) (7, 7) (13, 13) (7, 7) (12, 13) (13, 13)

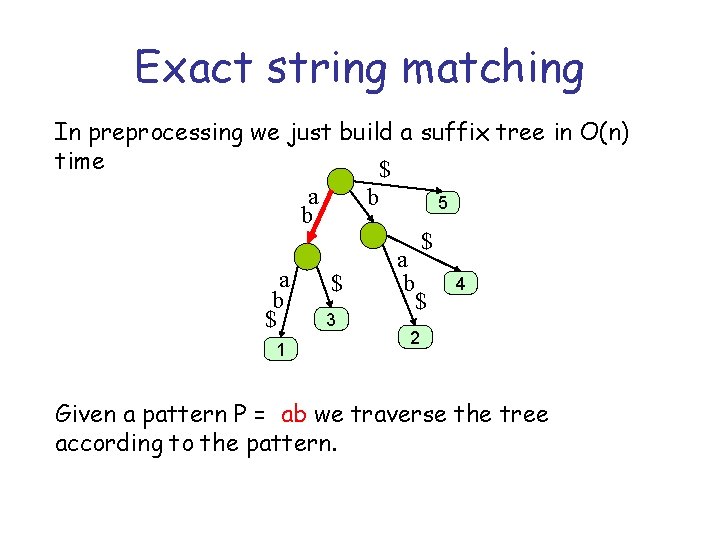
What can we do with it ? Exact string matching: Given a Text T, |T| = n, preprocess it such that when a pattern P, |P|=m, arrives you can quickly decide if it occurs in T. We may also want to find all occurrences of P in T

Exact string matching In preprocessing we just build a suffix tree in O(n) time $ a b 5 b $ a a 4 $ b b $ 3 $ 1 2 Given a pattern P = ab we traverse the tree according to the pattern.

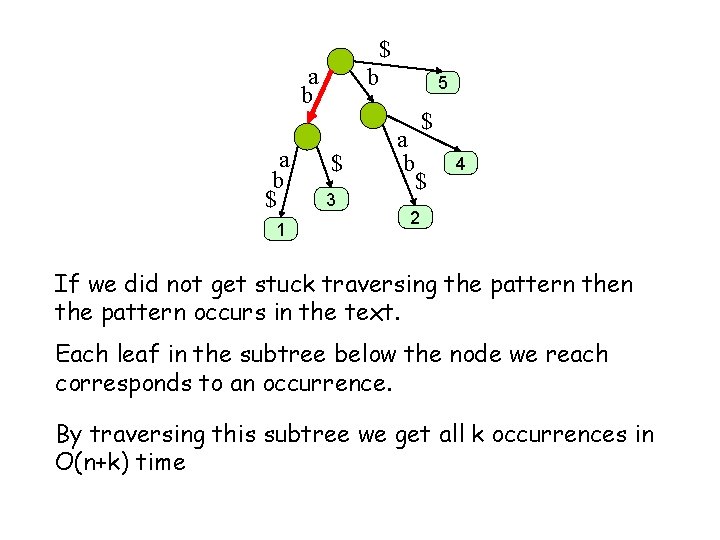
$ a b $ 1 b $ 3 5 $ a b $ 4 2 If we did not get stuck traversing the pattern occurs in the text. Each leaf in the subtree below the node we reach corresponds to an occurrence. By traversing this subtree we get all k occurrences in O(n+k) time

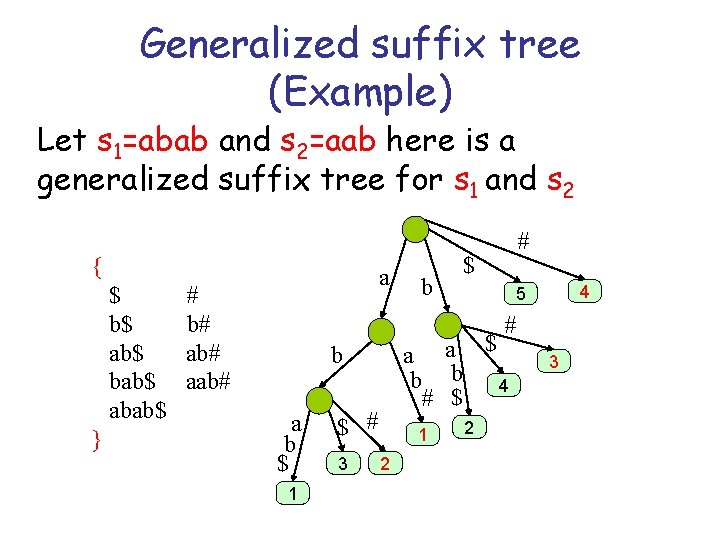
Generalized suffix tree Given a set of strings S a generalized suffix tree of S is a compressed trie of all suffixes of s S To associate each suffix with a unique string in S add a different special char to each s

Generalized suffix tree (Example) Let s 1=abab and s 2=aab here is a generalized suffix tree for s 1 and s 2 { $ b$ ab$ bab$ abab$ } a # b# aab# b # $ 4 5 # a a $ b b 4 # $ b a b $ 1 $ # 3 1 2 2 3

So what can we do with it ? Matching a pattern against a database of strings

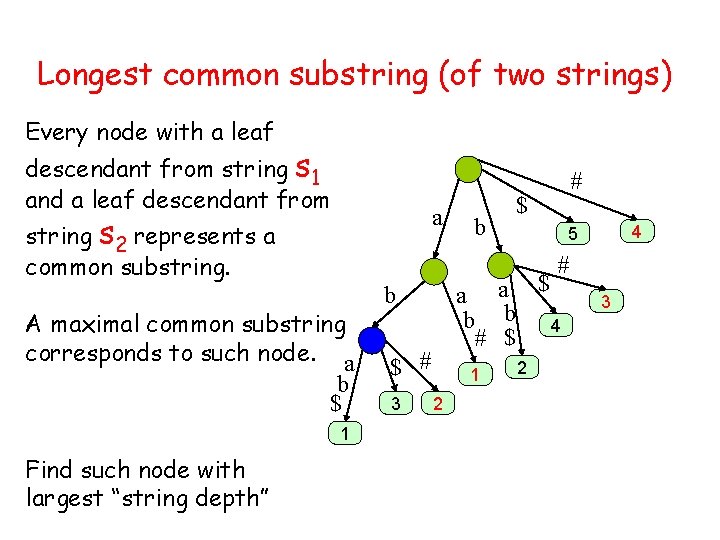
Longest common substring (of two strings) Every node with a leaf descendant from string s 1 and a leaf descendant from a string s 2 represents a common substring. $ 4 5 # A maximal common substring corresponds to such node. a b $ 1 Find such node with largest “string depth” b # a a $ b b 4 # $ b $ # 3 1 2 2 3

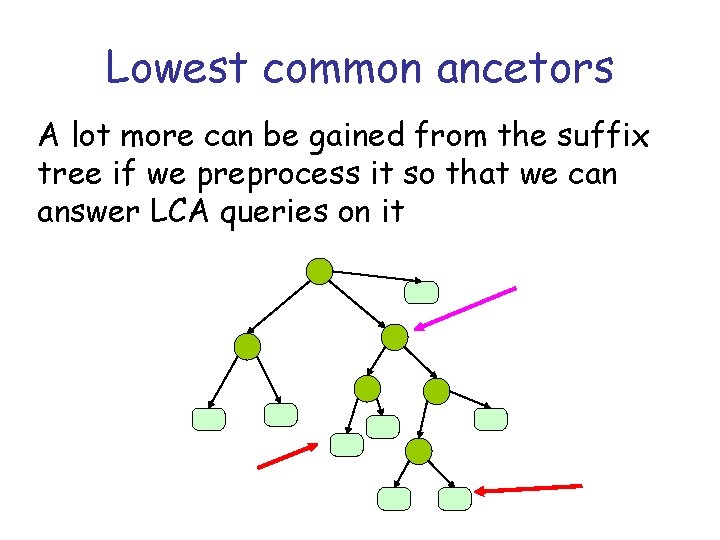
Lowest common ancetors A lot more can be gained from the suffix tree if we preprocess it so that we can answer LCA queries on it

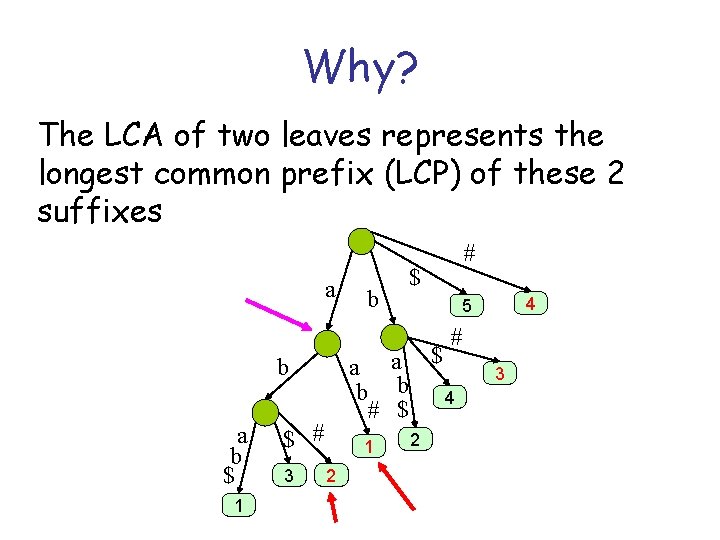
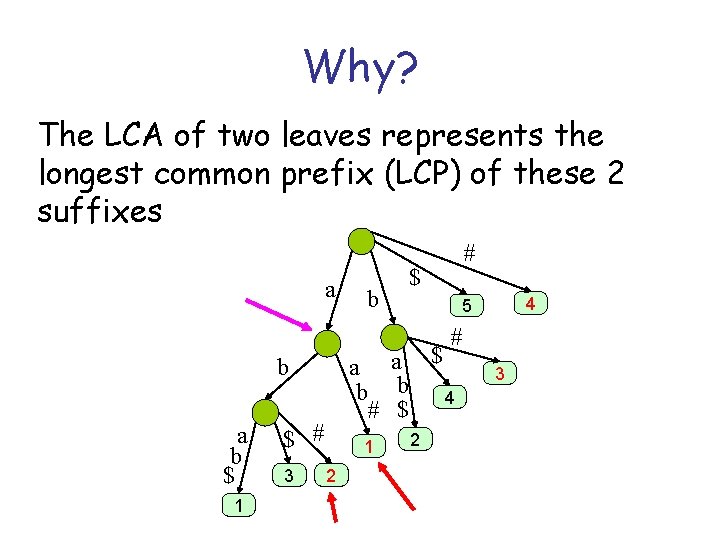
Why? The LCA of two leaves represents the longest common prefix (LCP) of these 2 suffixes a b # $ 4 5 # a a $ b b 4 # $ b a b $ 1 $ # 3 1 2 2 3

Lowest common ancestors

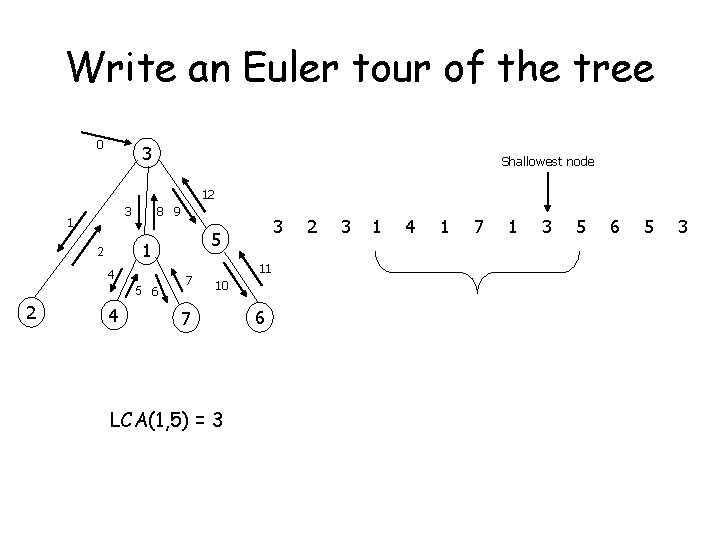
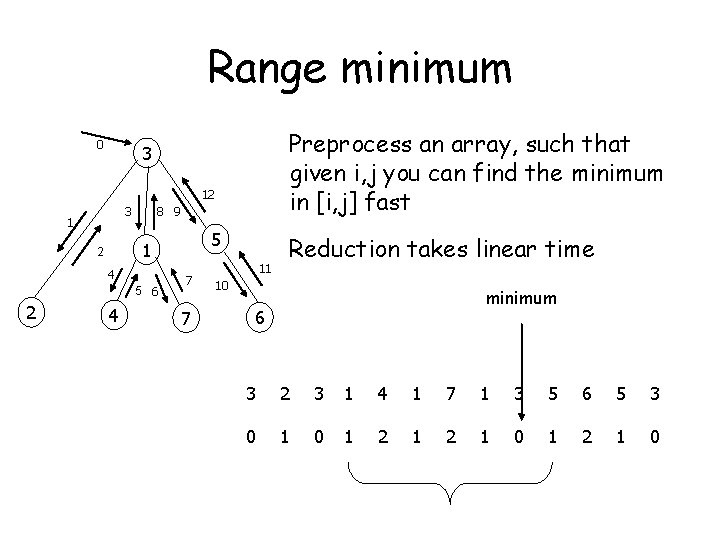
Write an Euler tour of the tree 0 3 Shallowest node 12 8 9 3 1 1 2 4 5 6 2 4 3 5 7 11 10 7 LCA(1, 5) = 3 6 2 3 1 4 1 7 1 3 5 6 5 3

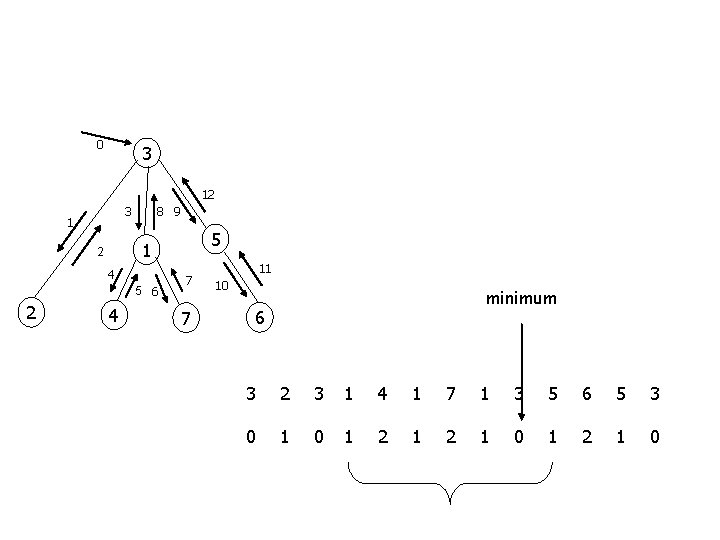
0 3 12 8 9 3 1 4 5 6 2 5 1 2 4 7 7 11 10 minimum 6 3 2 3 1 4 1 7 1 3 5 6 5 3 0 1 2 1 0

Range minimum 0 Preprocess an array, such that given i, j you can find the minimum in [i, j] fast 3 12 8 9 3 1 4 5 6 2 5 1 2 4 7 7 11 Reduction takes linear time 10 minimum 6 3 2 3 1 4 1 7 1 3 5 6 5 3 0 1 2 1 0

Trivial algorithms for RMQ • O(n) space, O(n) query time • O(n 2) space, O(1) query time

Less trivial algorithms to RMQ • Try to use O(nlog(n)) space to do a query in O(1) time. .

Lowest common ancetors A lot more can be gained from the suffix tree if we preprocess it so that we can answer LCA queries on it

Why? The LCA of two leaves represents the longest common prefix (LCP) of these 2 suffixes a b # $ 4 5 # a a $ b b 4 # $ b a b $ 1 $ # 3 1 2 2 3

Finding maximal palindromes • A palindrome: caabaac, cbaabc • Want to find all maximal palindromes in a string s Let s = cbaaba The maximal palindrome with center between i-1 and i is the LCP of the suffix at position i of s and the suffix at position n-i+1 of sr

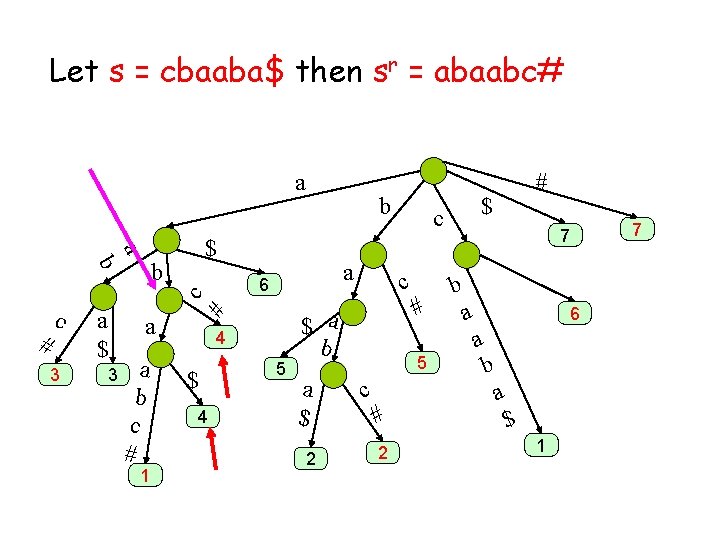
Maximal palindromes algorithm Prepare a generalized suffix tree for s = cbaaba$ and sr = abaabc# For every i, find the LCA of suffix i of s and suffix n-i+1 of sr

Let s = cbaaba$ then sr = abaabc# a a $ # 3 a $ 3 a a b c # 1 # c a 6 c b b 4 $ 4 b 5 $ a b a $ 2 $ c c # # 7 b a 6 a 5 c # 2 b a $ 1 7

Analysis O(n) time to identify all palindromes

• In fact we have seen binary tries already • In מבוא מורחב

Huffman trees/codes

Compression Represent data as a sequence of 0’s and 1’s Sequence: BACADAEAFABBAAAGAH A fixed length code: A 000 B 001 C 010 D 011 E 100 F 101 G 110 H 111 Encoding of sequence: 00100000110000010100000100100000110000111 The Encoding is 18 x 3=54 bits long. Can we make the encoding shorter?

Variable Length Code Make use of frequencies. Frequency of A=8, B=3, others 1. A 0 B 100 C 1010 D 1011 E 1100 F 1101 G 1110 H 1111 Example: BACADAEAFABBAAAGAH 10001011011000110101001000001111 42 bits (20% shorter) But how do we decode?

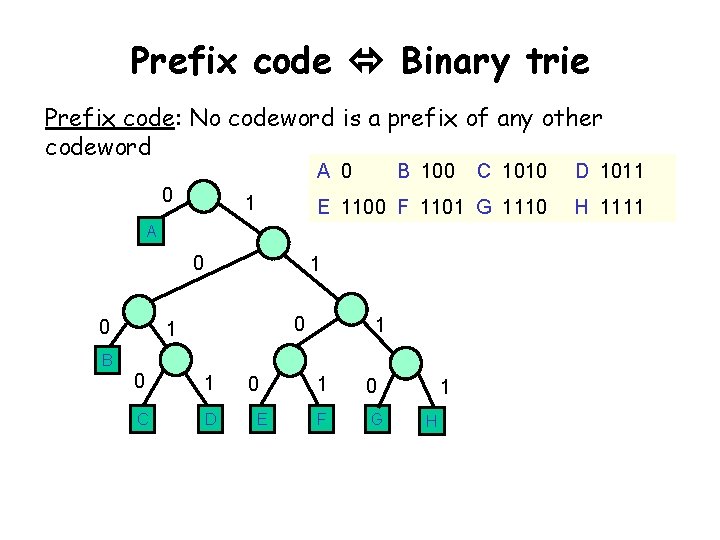
Prefix code Binary trie Prefix code: No codeword is a prefix of any other codeword A 0 0 1 B 100 C 1010 D 1011 E 1100 F 1101 G 1110 H 1111 A 0 0 1 1 B 0 1 C D 0 E 1 F 0 G 1 H

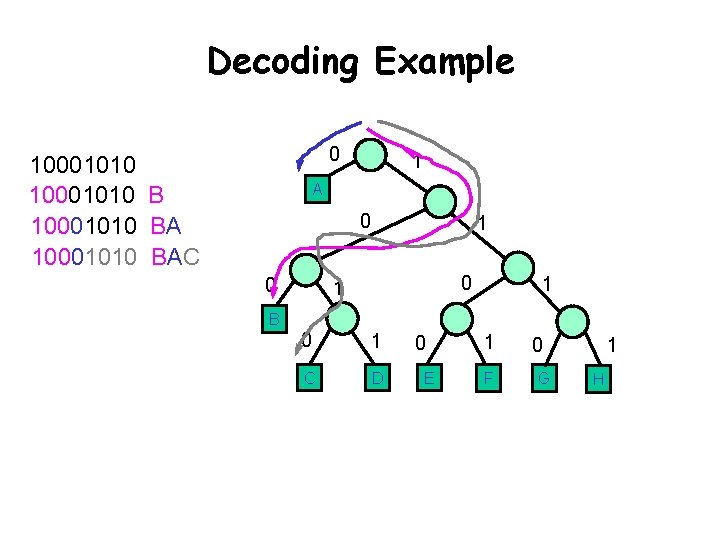
Decoding Example 0 10001010 BAC 1 A 0 0 1 1 B 0 1 C D 0 E 1 F 0 G 1 H

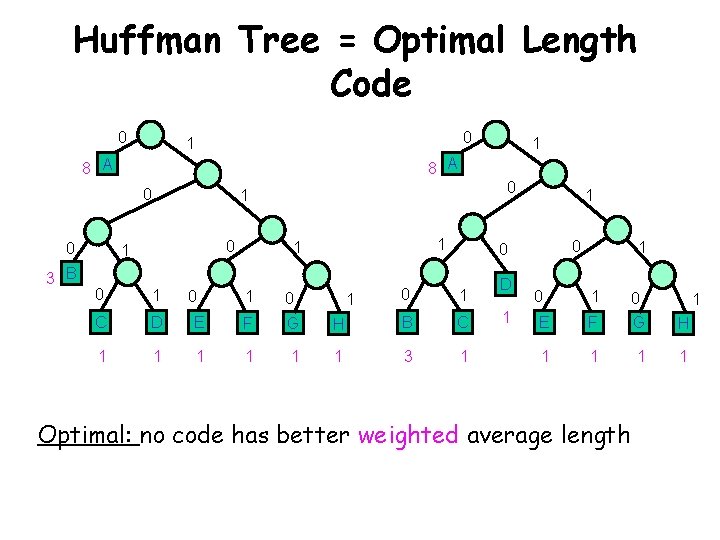
Huffman Tree = Optimal Length Code 0 0 1 8 A 0 0 3 B 1 0 1 0 1 C D 1 1 1 0 E F G 1 1 1 0 0 0 1 H B C 1 3 1 1 1 D 1 1 1 0 E F G H 1 1 0 Optimal: no code has better weighted average length 1

Huffman’s Algorithm Build tree bottom-up, so that lowest weight leaves are farthest from the root. Repeatedly: Find two trees of lowest weight. merge them to form a new tree whose weight is the sum of their weights.

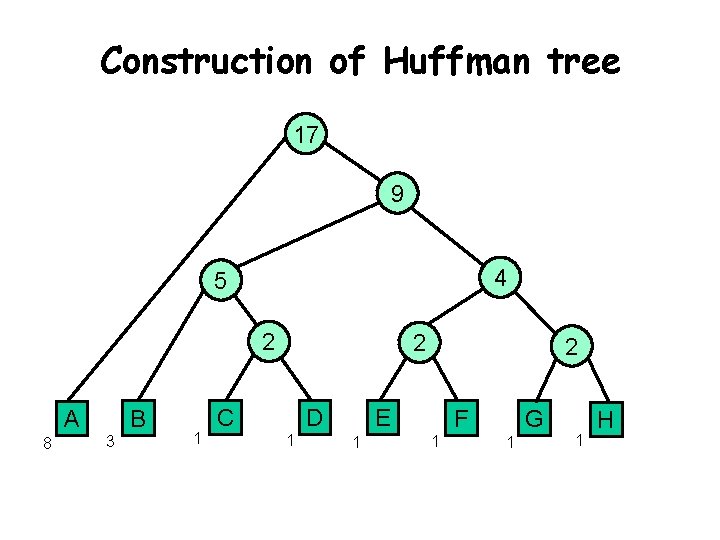
Construction of Huffman tree 17 9 4 5 2 B A 8 3 1 2 C D 1 2 E 1 F 1 G 1 1 H

Two questions • Why does the algorithm produce the best tree ? • How do you implement it efficiently ?

Implementation Huffman(C) n ← |C| Q←C for i ← 1 to n-1 do new(z) left(z) ← x ← delete-min(Q) right(z) ← y ← delete-min(Q) f(z) ← f(x) + f(y) insert(z, Q) return delete-min(Q)

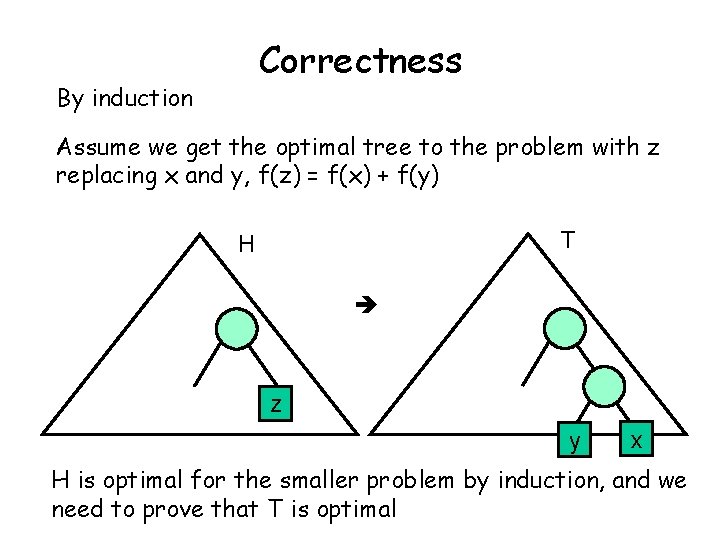
Correctness By induction Assume we get the optimal tree to the problem with z replacing x and y, f(z) = f(x) + f(y) T H z y x H is optimal for the smaller problem by induction, and we need to prove that T is optimal

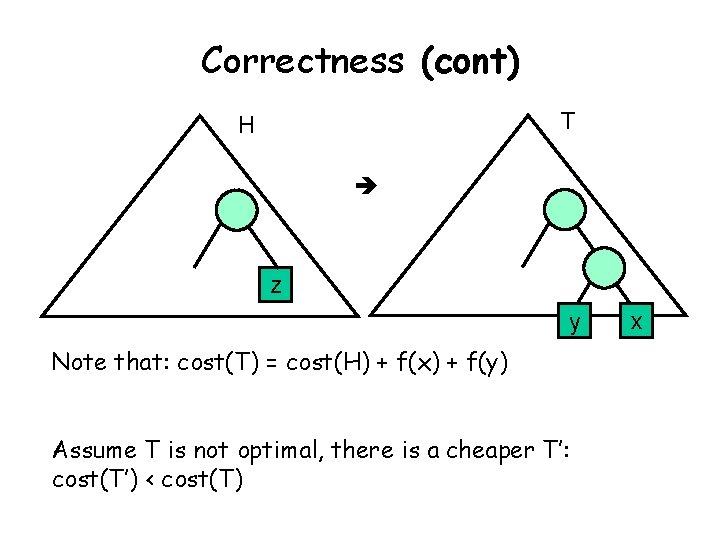
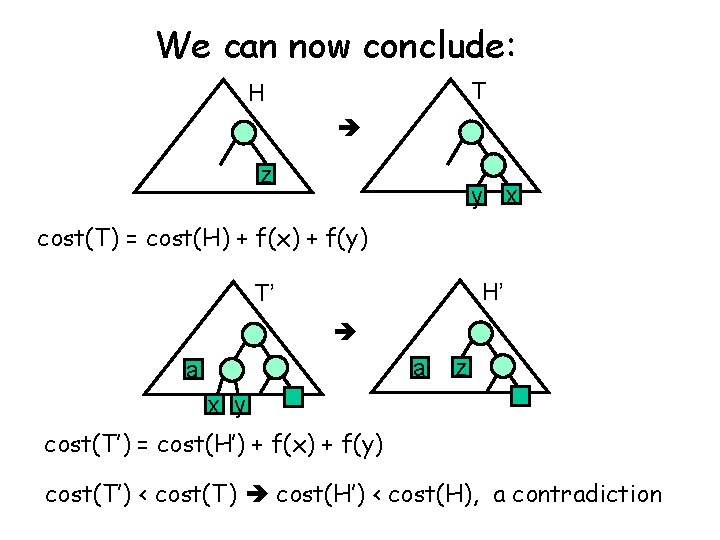
Correctness (cont) T H z y Note that: cost(T) = cost(H) + f(x) + f(y) Assume T is not optimal, there is a cheaper T’: cost(T’) < cost(T) x

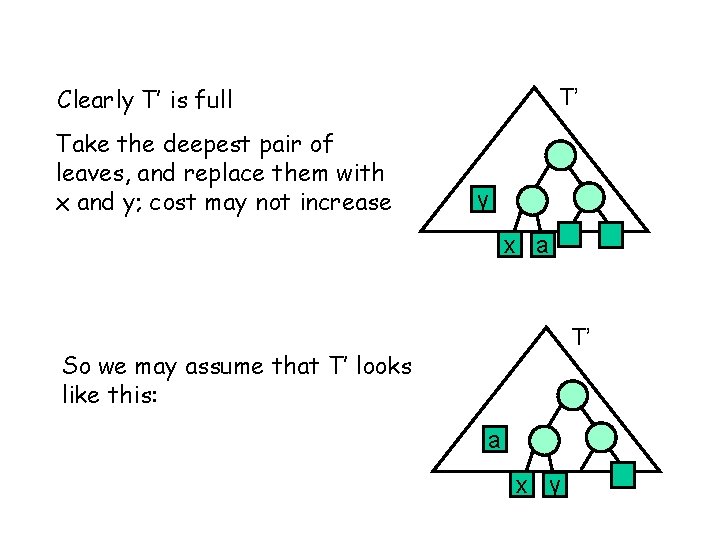
Clearly T’ is full Take the deepest pair of leaves, and replace them with x and y; cost may not increase T’ y x a T’ So we may assume that T’ looks like this: a x y

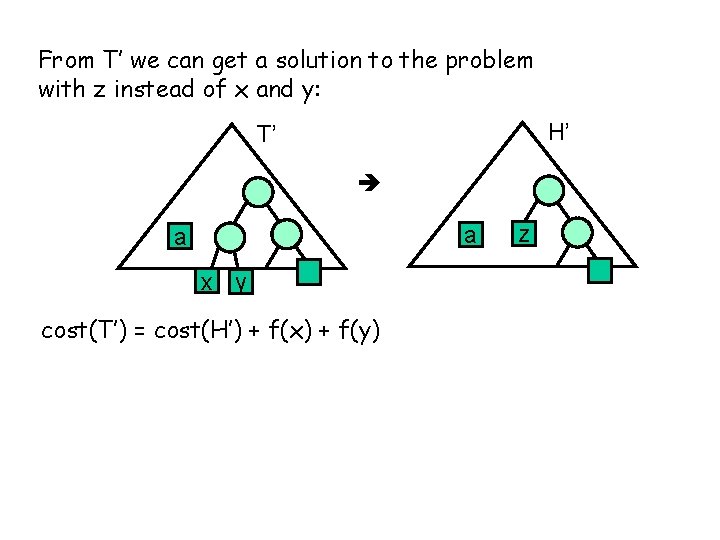
From T’ we can get a solution to the problem with z instead of x and y: H’ T’ a a x y cost(T’) = cost(H’) + f(x) + f(y) z

We can now conclude: T H z y x cost(T) = cost(H) + f(x) + f(y) H’ T’ a a z x y cost(T’) = cost(H’) + f(x) + f(y) cost(T’) < cost(T) cost(H’) < cost(H), a contradiction

Compression Huffman code just uses the frequencies, does not use context We will gain much more if we use context

Compression S[1. . n]= aabcbbabbsbabcbbbbabbabcbbabbabbsb… aabcbbabbsb (2, 5) bbabbabcbbabbabbsb…

Compression S[1. . n]= aabcbbabbsbabcbbbbabbabcbbabbabbsb… aabcbbabbsb (2, 5) bbabbabcbbabbabbsb… נגדיר Priori=S[i. . i+Li-1] הרישה הארוכה ביותר אשר מופיעה כתת מחרוזת - S[1. . i-1] ב

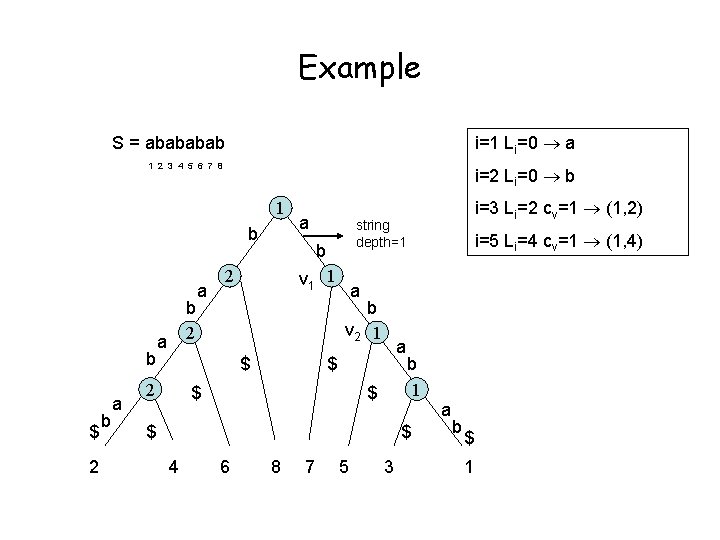
Compression S[1. . n]= aabcbbabbsbabcbbbbabbabcbbabbabbsb… aabcbbabbsb (2, 5) bbabbabcbbabbabbsb… נגדיר Priori=S[i. . i+Li-1] הרישה הארוכה ביותר Prior 12=abcbb מחרוזת כתת מופיעה אשר L 12=5 - S[1. . i-1] ב

Compression S[1. . m]= aabcbbabbsbabcbbbbabbabcbbabbabbsb… i=12 aabcbbabbsb (2, 5) bbabbabcbbabbabbsb… (s 12, L 12) נגדיר Priori=S[i. . i+Li-1] הרישה הארוכה ביותר Prior 12=abcbb מחרוזת כתת מופיעה אשר L 12=5 - S[1. . i-1] ב s 12=2

“Ziv-Lempel” compression For (i=1 ; i<=n ; ; ) {Compute (si, Li) if Li>1 {output(si, Li); i=i+Li}; else {output(S[i]); i=i+1}} aabcbbabbsbabbbbbabbabcbbabbabbsb… aabcbb bs (si, Li) איך לחשב את (2, 2) (6, 4)

Implementation using suffix tree Before compression: • Build a suffix tree T for S. • For each node v, compute cv : – the smallest leaf index in v’s subtree. – the starting position of the leftmost copy of the substring that labels the path from the root to v. • O(n) time.

root computing (si, Li): a |a| + cv ≤ i p S[ n] i. . . v cv i |a| leaf i

• To compute (si, Li), traverse the unique path in T that matches a prefix of S[i. . . n]: – Let: p - current point, v - first node at or below p. – Traverse as long as: string_length(p) + cv ≤ i. – At the last point p of traversal: Li = string_length(p), si = cv. • O(Li) time.

Example S = abab i=1 Li=0 a 1 2 3 4 5 6 7 8 i=2 Li=0 b 1 b $ 2 b a a 2 string depth=1 b 2 v 1 1 i=5 Li=4 cv=1 (1, 4) a b v 2 1 $ b b 2 a a i=3 Li=2 cv=1 (1, 2) a $ $ $ b 1 a $ $ 4 6 8 7 5 3 b $ 1

Suffix array • We loose some of the functionality but we save space. Let s = abab Sort the suffixes lexicographically: ab, abab, b, bab The suffix array gives the indices of the suffixes in sorted order 2 0 3 1

How do we build it ? • Build a suffix tree • Traverse the tree in in-order, lexicographically picking edges outgoing from each node and fill the suffix array. • O(n) time • Can also build it directly

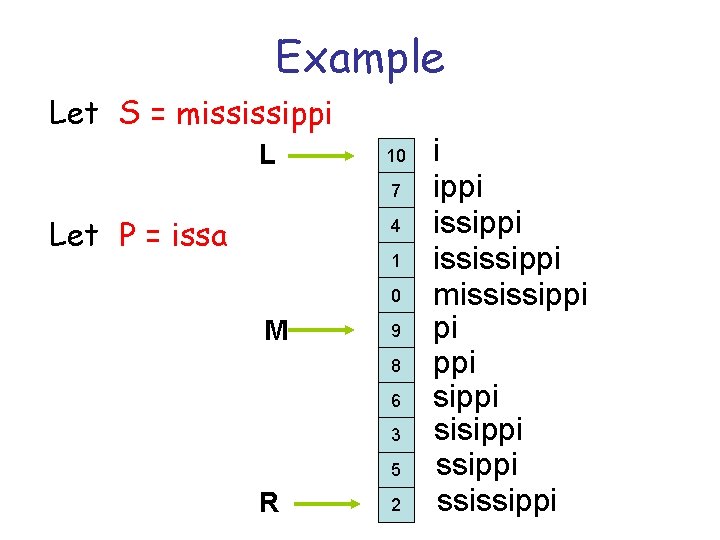
Example Let S = mississippi L 10 7 Let P = issa 4 1 0 M 9 8 6 3 5 R 2 i ippi ississippi mississippi pi ppi sisippi ssissippi

How do we search for a pattern ? • If P occurs in T then all its occurrences are consecutive in the suffix array. • Do a binary search on the suffix array • Takes O(mlogn) time • Can also do it in O(m+log(n)) with an additional array