Suffix Trees String any sequence of characters Substring

Suffix Trees • String … any sequence of characters. • Substring of string S … string composed of characters i through j, i <= j of S. § S = cater => ate is a substring. § car is not a substring. § Empty string is a substring of S.

Subsequence • Subsequence of string S … string composed of characters i 1 < i 2 < … < ik of S. § S = cater => ate is a subsequence. § car is a subsequence. § The empty string is a subsequence.

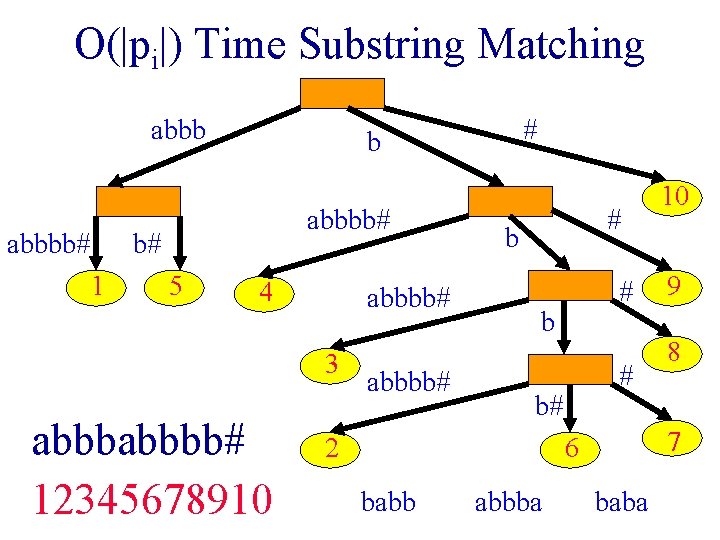
String/Pattern Matching • You are given a source string S. • Answer queries of the form: is the string pi a substring of S? • Knuth-Morris-Pratt (KMP) string matching. § O(|S| + | pi |) time per query. § O(n|S| + Si | pi |) time for n queries. • Suffix tree solution. § O(|S| + Si | pi |) time for n queries.

String/Pattern Matching • KMP preprocesses the query string pi, whereas the suffix tree method preprocesses the source string S. • An application of string matching. § § Genome project. Databank of strings (gene sequences). Character set is ATGF. Determine if a “new” sequence is a substring of a databank sequence.

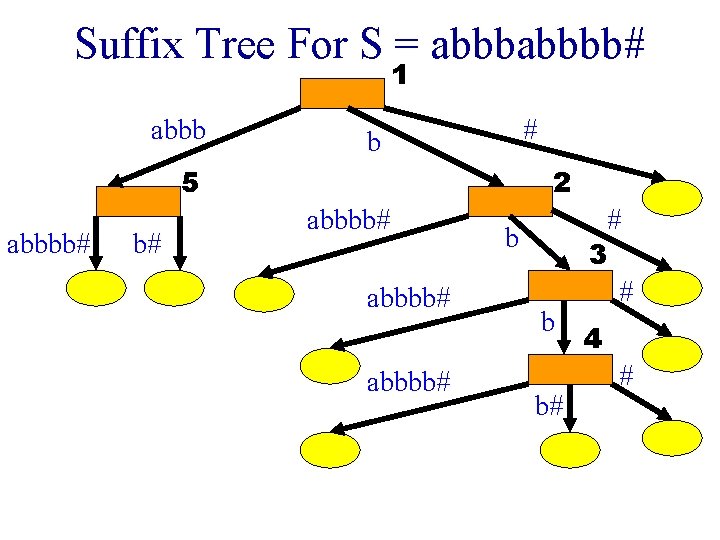
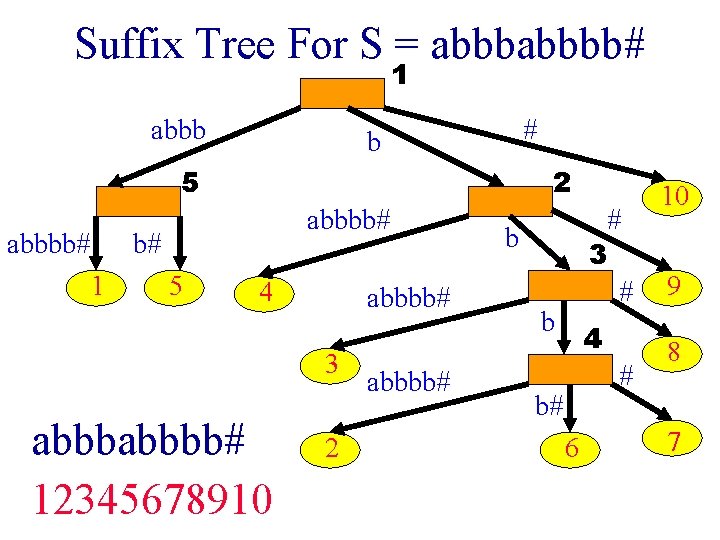
Definition Of Suffix Tree • Compressed trie with edge information. • Keys are the nonempty suffixes of a given string S. • Nonempty suffixes of S = sleeper are: § § § sleeper per, and r.

String Matching & Suffixes • pi is a substring of S iff pi is a prefix of some suffix of S. • Nonempty suffixes of S = sleeper are: § § § sleeper per, and r. • Which of these are substrings of S? § leep, eepe, leap, peel

Last Character Of S Repeats • When the last character of S appears more than once in S, S has at least one suffix that is a proper prefix of another suffix. • S = creeper § creeper, per, r • When the last character of S appears more than once in S, use an end of string character # to overcome this problem. • S = creeper# § creeper#, per#, r#, #

Suffix Tree For S = abbbb# 1 abbb # b 5 abbbb# b# 2 abbbb# b b b# # 3 # 4 #

Suffix Tree For S = abbbb# 1 abbb # b 5 abbbb# 2 abbbb# b# 1 5 4 abbbb# 3 abbbb# 12345678910 2 abbbb# # 3 # b b 4 # b# 6 10 9 8 7

Suffix Tree For S = abbbb# 1 1 abbb 5 1 abbbb# 5 2 4 b# 1 # b 4 abbbb# 3 abbbb# 12345678910 2 b 8 2 abbbb# # 3 # b 4 # b# 6 10 9 8 7

Suffix Tree Construction • See Web write up for algorithm. • Time complexity § § § |S| = n, alphabet size = r. O(nr) using array nodes. This is O(n) for r a constant (or r <= c). O(n) expected time using a hash table. O(n) time algorithm for large r in reference cited in Web write up.

O(|pi|) Time Substring Matching abbbb# b# 1 5 # b 4 abbbb# 3 abbbb# 12345678910 abbbb# # b # b# 2 abbba 9 8 7 6 babb 10 baba

Find All Occurrences Of pi • Search suffix tree for pi. • Suppose the search for pi is successful. • When search terminates at an element node, pi appears exactly once in the source string S.

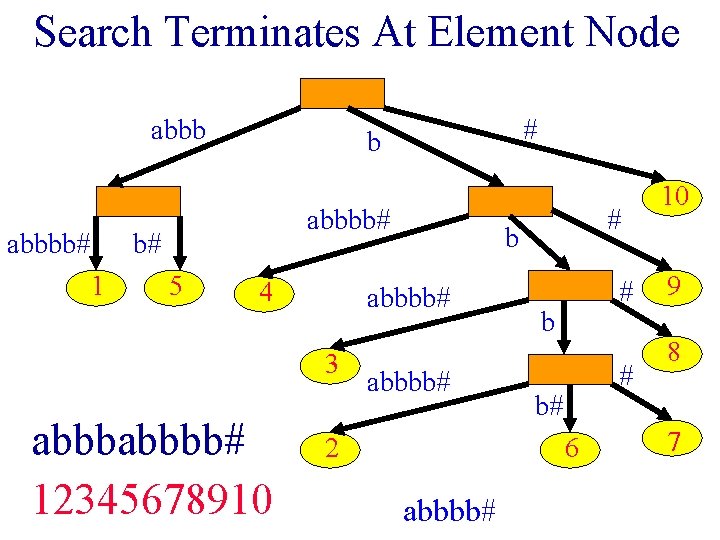
Search Terminates At Element Node abbbb# b# 1 # b 5 4 abbbb# 12345678910 b abbbb# 3 # abbbb# 2 # b# 6 abbbb# 10 9 8 7

Search Terminates At Branch Node • When the search for pi terminates at a branch node, each element node in the subtree rooted at this branch node gives a different occurrence of pi.

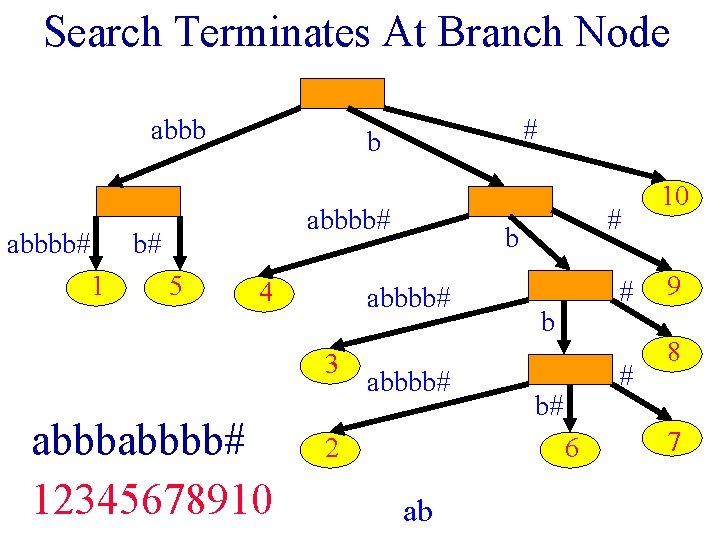
Search Terminates At Branch Node abbbb# b# 1 # b 5 4 abbbb# 12345678910 b abbbb# 3 # abbbb# 2 # b# 6 ab 10 9 8 7

Find All Occurrences Of pi • To find all occurrences of pi in time linear in the length of pi and linear in the number of occurrences of pi, augment suffix tree: § Link all element nodes into a chain in inorder. § Each branch node keeps a pointer to the left most and right most element node in its subtree.

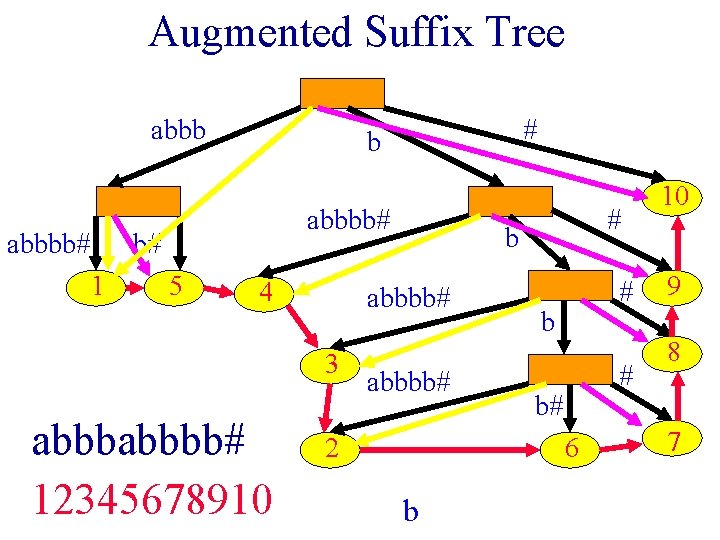
Augmented Suffix Tree abbbb# b# 1 # b 5 4 abbbb# 12345678910 b abbbb# 3 # abbbb# 2 # b# 6 b 10 9 8 7

Longest Repeating Substring • Find longest substring of S that occurs more than m > 1 times in S. • Label branch nodes with number of element nodes in subtree. • Find branch node with label >= m and max char# field.

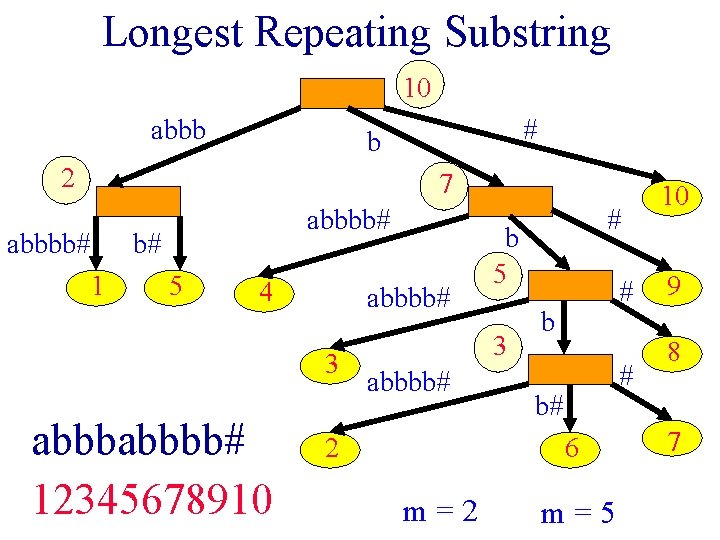
Longest Repeating Substring 10 abbb # b 2 7 abbbb# b# 1 5 4 abbbb# 3 abbbb# 12345678910 b 5 3 abbbb# 2 # # b# 6 m=2 m=5 10 9 8 7

Longest Common Substring • Given two strings S and T. • Find the longest common substring. • S = carport, T = airports § Longest common substring = rport § Longest common subsequence = arport • Longest common subsequence may be found in O(|S|*|T|) time using dynamic programming. • Longest common substring may be found in O(|S|+|T|) time using a suffix tree.

Longest Common Substring • Let $ be a new symbol. • Construct the suffix tree for the string U = S$T#. § U = carport$airports# § No repeating substring includes $. § Find longest repeating substring that is both to left and right of $. • Find branch node that has max char# and has at least one element node in its subtree that represents a suffix that begins in S as well as at least one that begins in T.