Suffix arrays Suffix array We loose some of













![Substring search using the BWT P[ j ] (Count the pattern occurrences) C P Substring search using the BWT P[ j ] (Count the pattern occurrences) C P](https://slidetodoc.com/presentation_image_h2/a9b6189774c2fbee99074d279f18a555/image-63.jpg)





- Slides: 72

Suffix arrays

Suffix array • We loose some of the functionality but we save space. Let s = abab Sort the suffixes lexicographically: ab, abab, b, bab The suffix array gives the indices of the suffixes in sorted order 2 0 3 1

How do we build it ? • Build a suffix tree • Traverse the tree in DFS, lexicographically picking edges outgoing from each node and fill the suffix array. • O(n) time

How do we search for a pattern ? • If P occurs in T then all its occurrences are consecutive in the suffix array. • Do a binary search on the suffix array • Takes O(mlogn) time

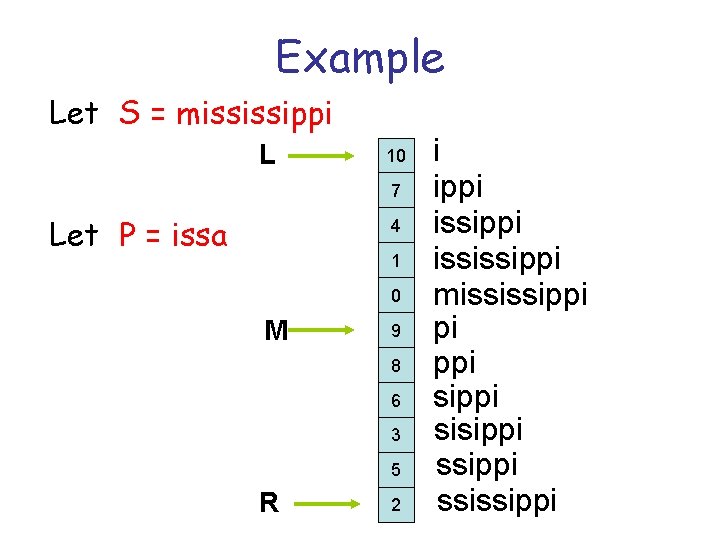
Example Let S = mississippi L 10 7 Let P = issa 4 1 0 M 9 8 6 3 5 R 2 i ippi ississippi mississippi pi ppi sisippi ssissippi

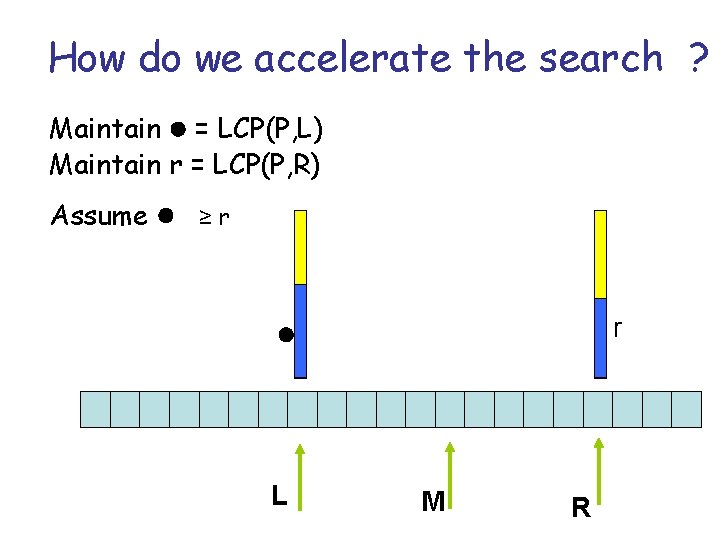
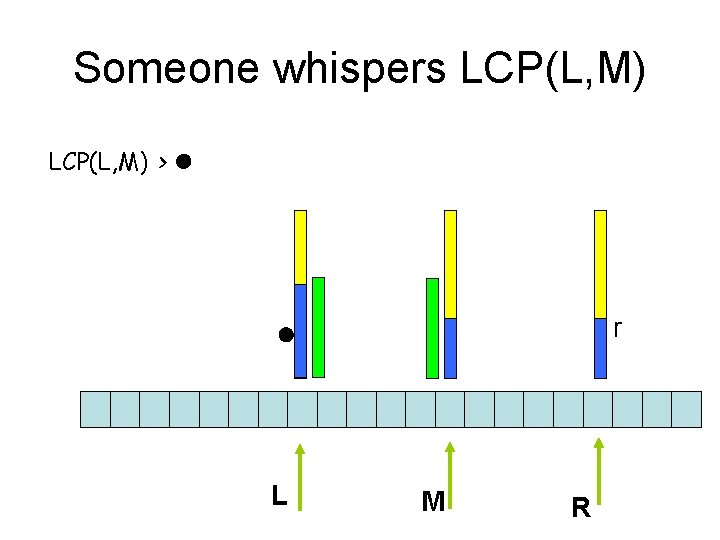
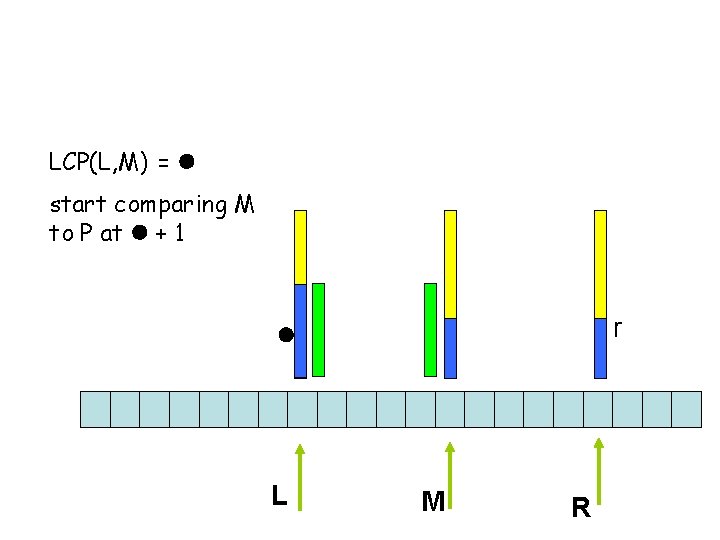
How do we accelerate the search ? Maintain l = LCP(P, L) Maintain r = LCP(P, R) Assume l ≥ r r l L M R

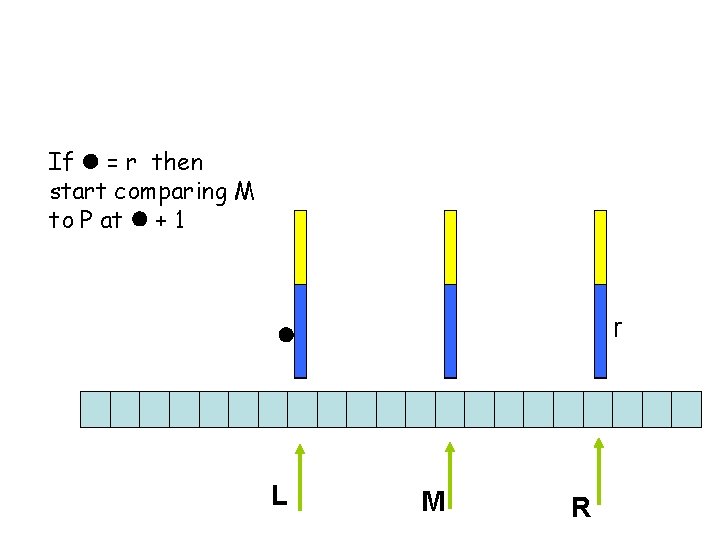
If l = r then start comparing M to P at l + 1 r l L M R

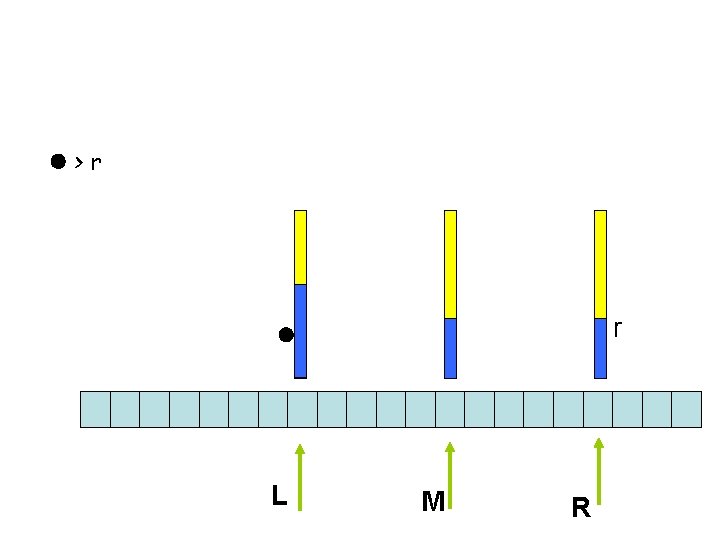
l>r r l L M R

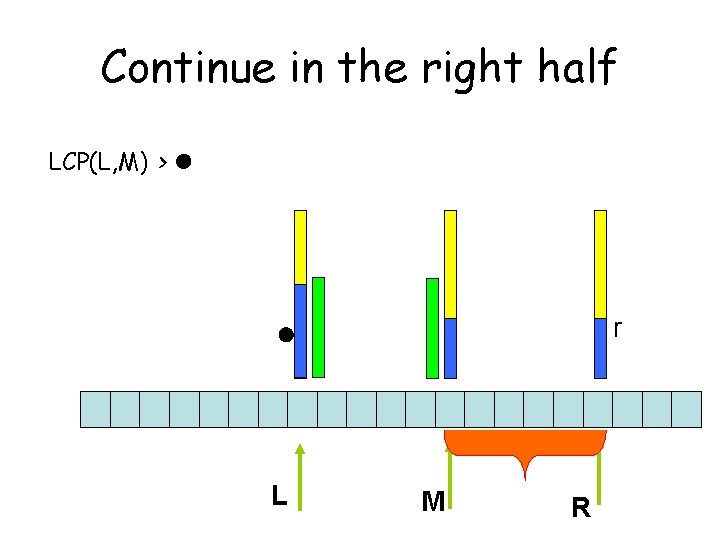
Someone whispers LCP(L, M) > l r l L M R

Continue in the right half LCP(L, M) > l r l L M R

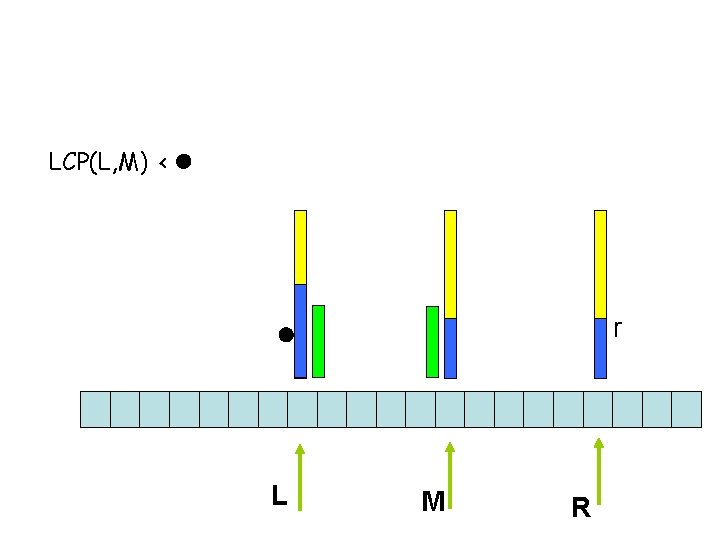
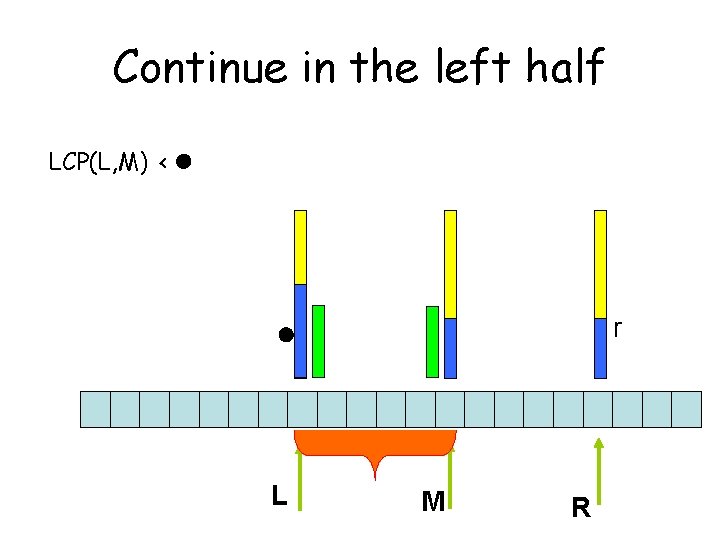
LCP(L, M) < l r l L M R

Continue in the left half LCP(L, M) < l r l L M R

LCP(L, M) = l start comparing M to P at l + 1 r l L M R

Analysis If we do more than a single comparison in an iteration then max(l, r ) grows by 1 for each comparison O(m + logn) time

Construct the suffix array without the suffix tree

Linear time construction Recursively ? Say we want to sort only suffixes that start at even positions ?

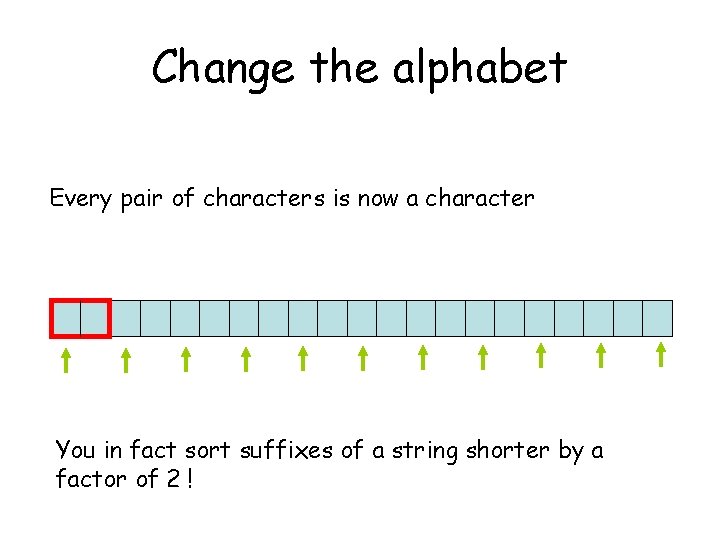
Change the alphabet Every pair of characters is now a character You in fact sort suffixes of a string shorter by a factor of 2 !

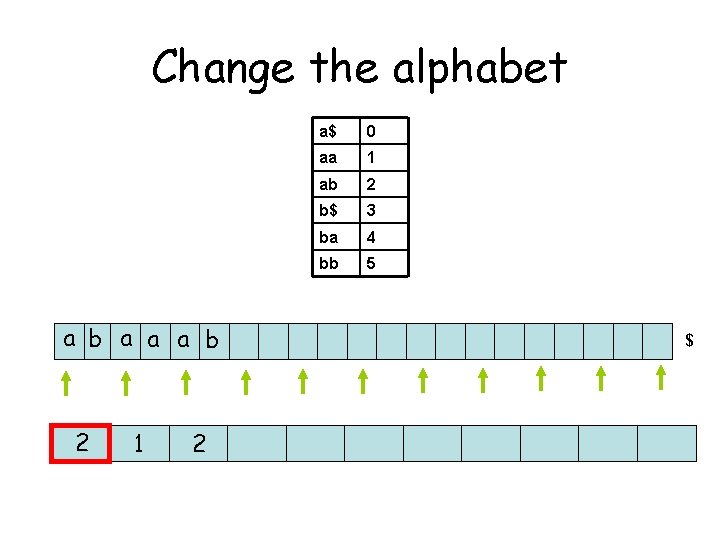
Change the alphabet a b a a a b 2 1 2 a$ 0 aa 1 ab 2 b$ 3 ba 4 bb 5 $

But we do not gain anything…

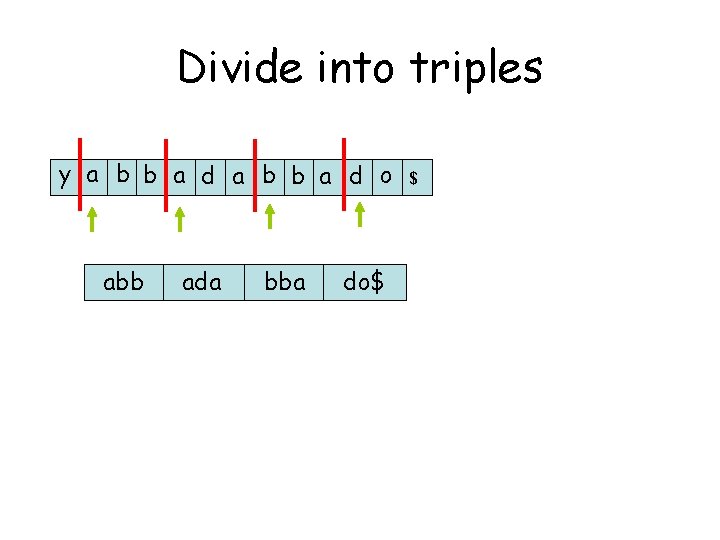
Divide into triples y a b b a d o abb ada bba do$ $

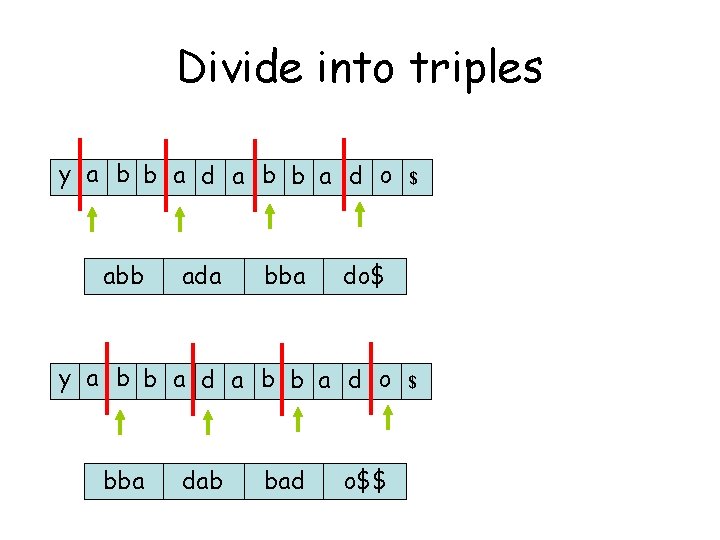
Divide into triples y a b b a d o abb ada bba do$ y a b b a d o bba dab bad $ o$$ $

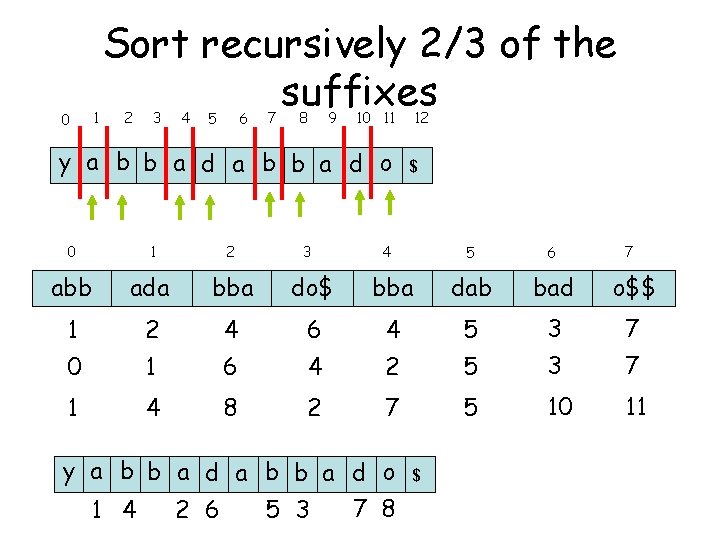
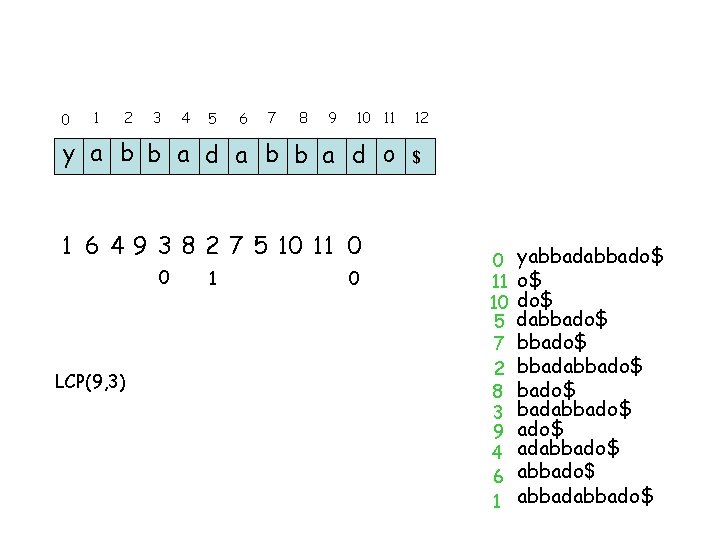
0 1 Sort recursively 2/3 of the suffixes 2 3 4 5 6 7 8 9 10 11 y a b b a d o 0 1 2 3 abb ada bba do$ 1 2 4 0 1 1 4 12 $ 4 7 5 6 bba dab bad o$$ 6 4 5 3 7 6 4 2 5 3 7 8 2 7 5 10 11 y a b b a d o 7 8 1 4 2 6 5 3 $

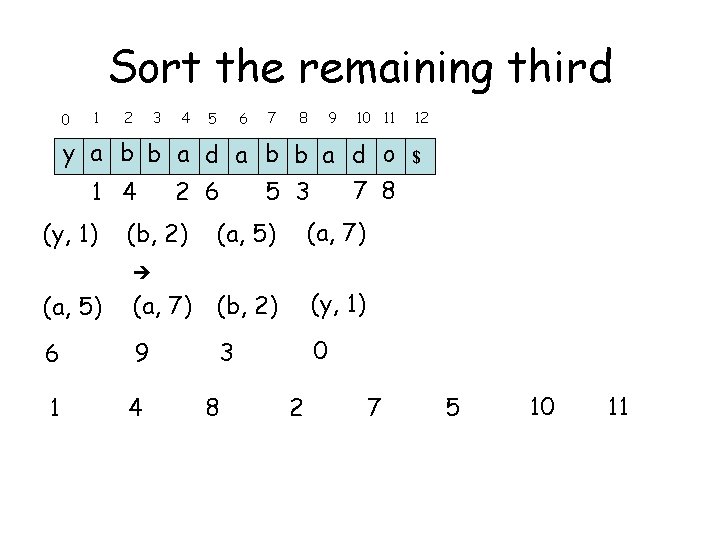
Sort the remaining third 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 (y, 1) (b, 2) (a, 5) (a, 7) 12 $ (a, 5) (a, 7) (b, 2) (y, 1) 6 9 3 0 1 4 8 2 7 5 10 11

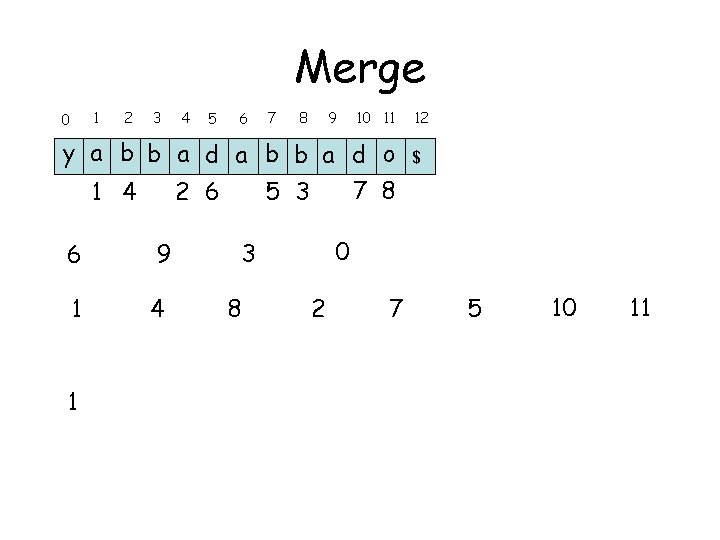
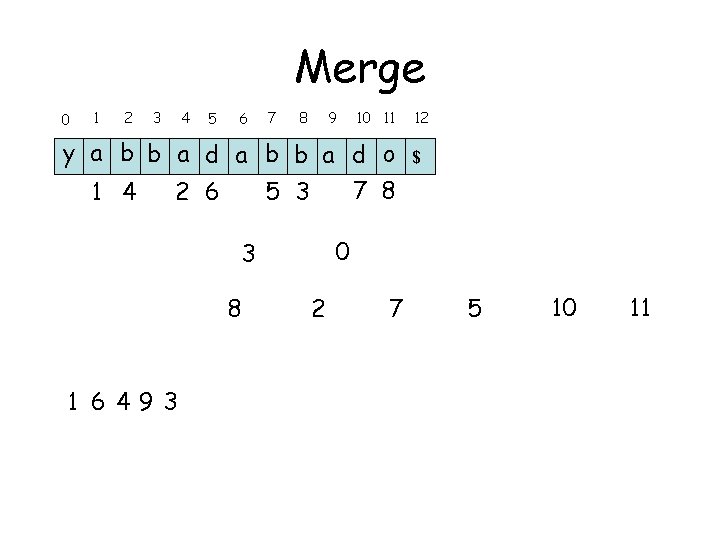
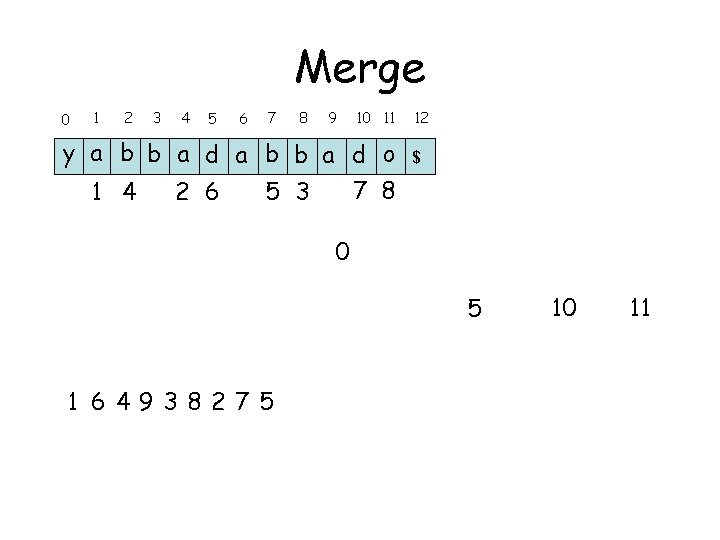
Merge 1 0 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 6 1 1 9 4 $ 0 3 8 12 2 7 5 10 11

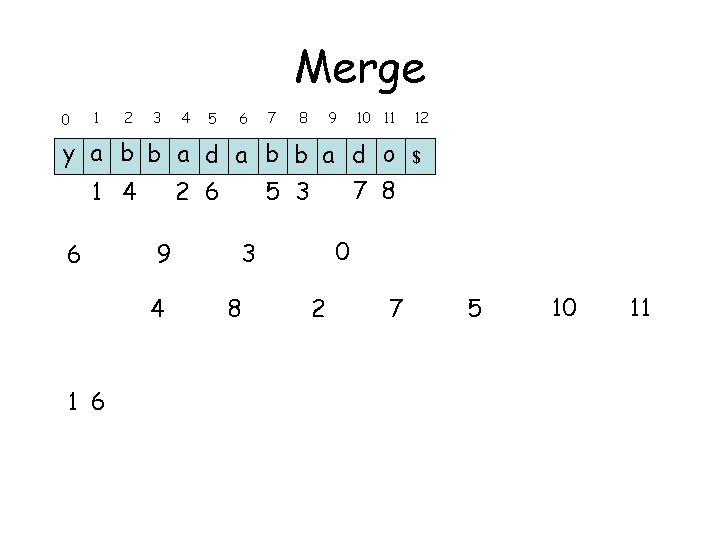
Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 6 9 4 1 6 $ 0 3 8 12 2 7 5 10 11

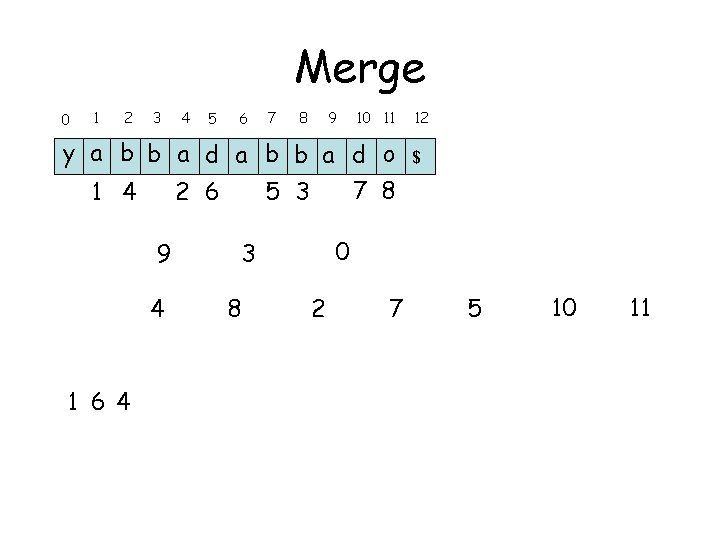
Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 9 4 1 64 $ 0 3 8 12 2 7 5 10 11

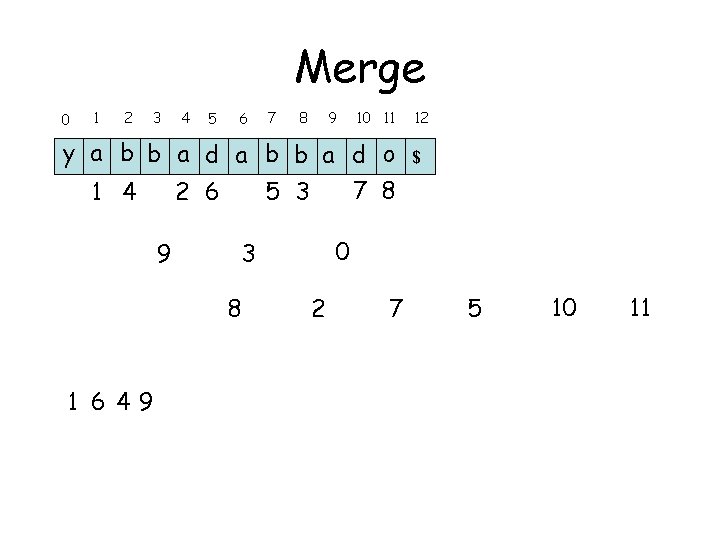
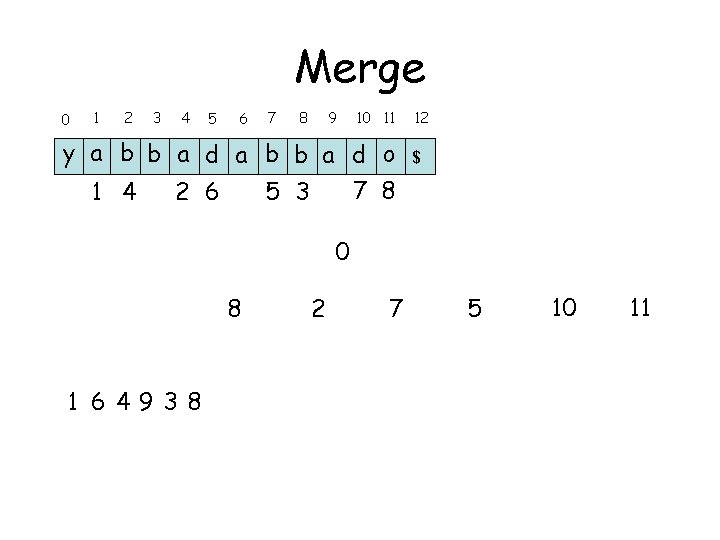
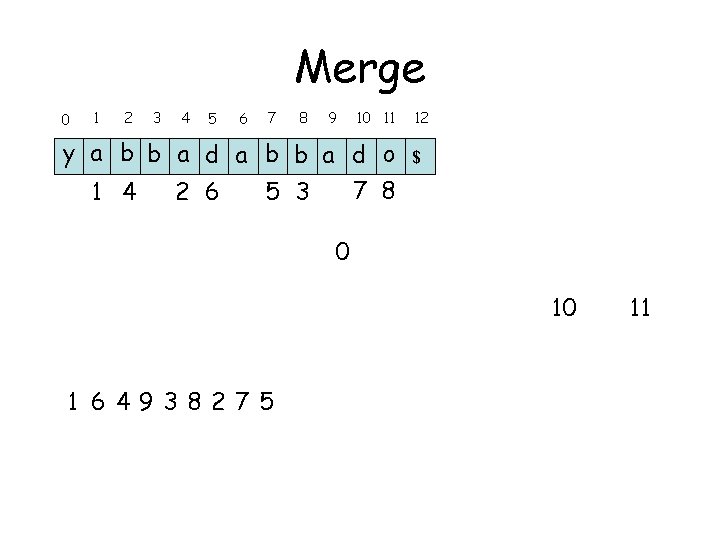
Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 9 1 649 $ 0 3 8 12 2 7 5 10 11

Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 1 6493 $ 0 3 8 12 2 7 5 10 11

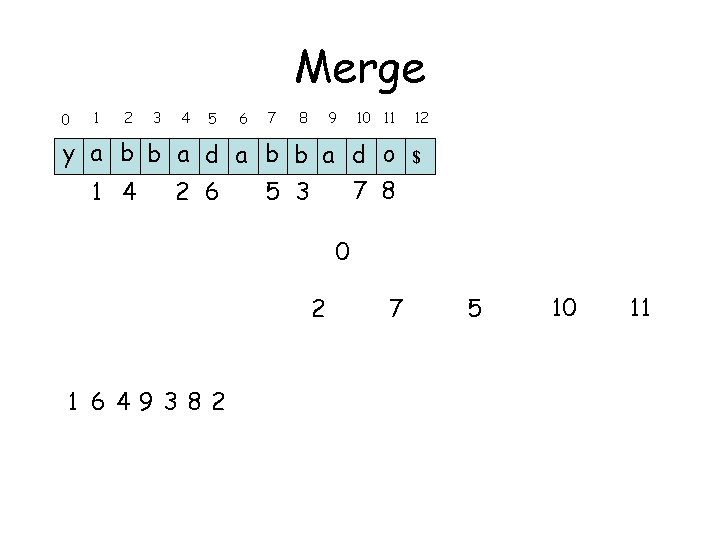
Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 12 $ 0 8 1 64938 2 7 5 10 11

Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 12 $ 0 2 1 649382 7 5 10 11

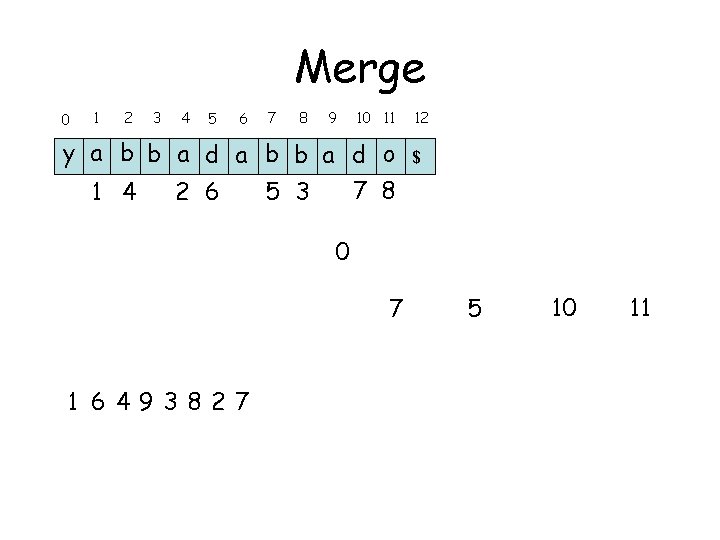
Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 12 $ 0 7 1 6493827 5 10 11

Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 12 $ 0 5 1 64938275 10 11

Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 12 $ 0 10 1 64938275 11

Merge 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 1 6 4 9 3 8 2 7 5 10 11 0 12 $

summary 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 7 8 1 4 2 6 5 3 12 $ 1 6 4 9 3 8 2 7 5 10 11 0 When comparing to a suffix with index 1 (mod 3) we compare the char and break ties by the ranks of the following suffixes When comparing to a suffix with index 2 (mod 3) we compare the char, the next char if there is a tie, and finally the ranks of the following suffixes

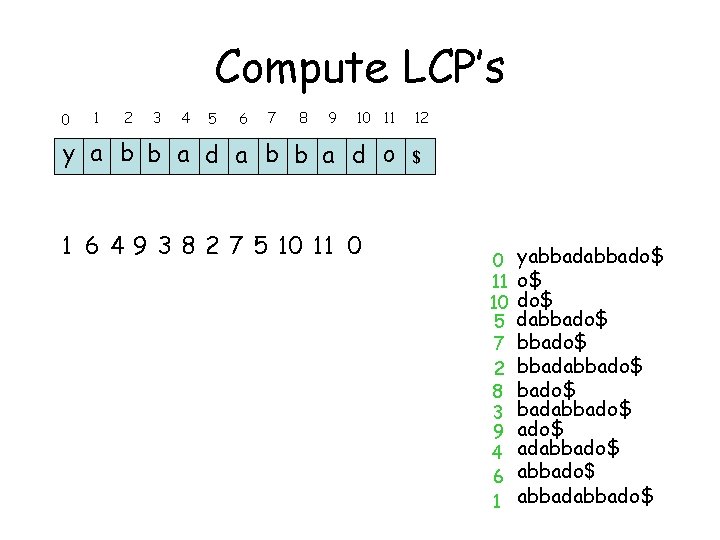
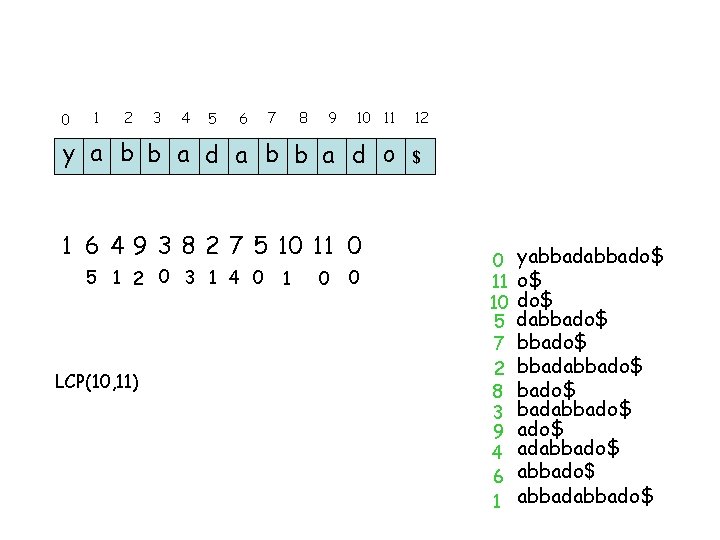
Compute LCP’s 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

Crucial observation 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 12 $ 1 6 4 9 3 8 2 7 5 10 11 0 LCP(i, j) = min {LCP(i, i+1), LCP(i+1, i+2), …. , LCP(j-1, j)} 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

Find LCP’s of consecutive suffixes 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 0 LCP(11, 0) 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

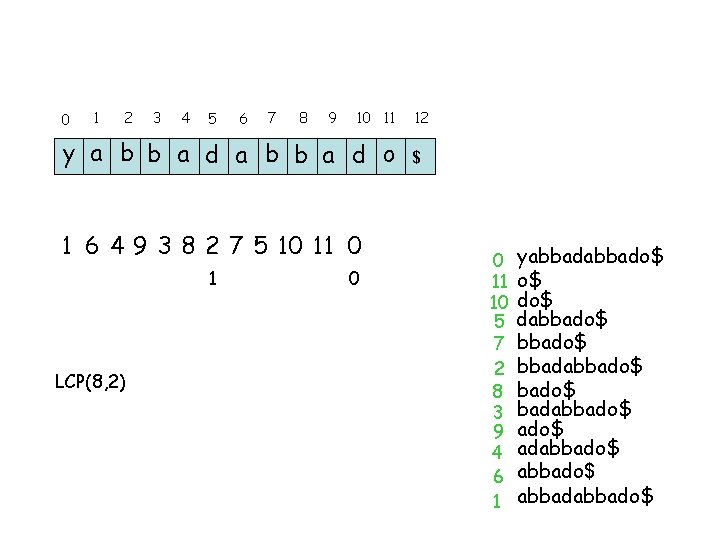
0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 1 LCP(8, 2) 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 0 LCP(9, 3) 1 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

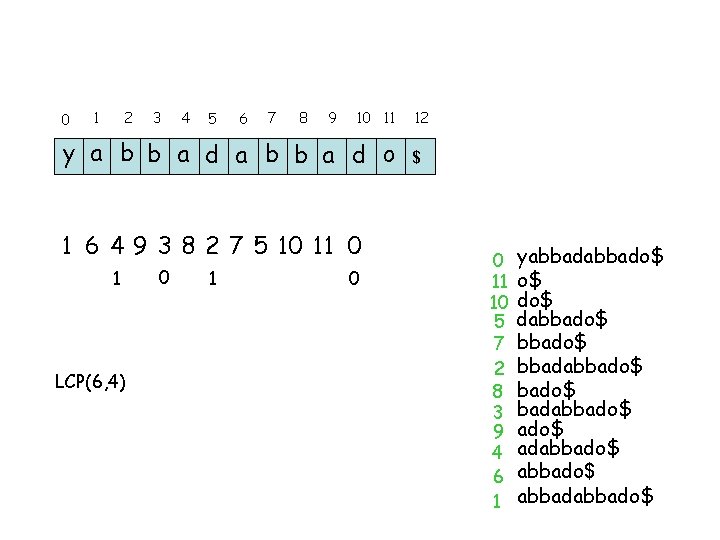
0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 1 LCP(6, 4) 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

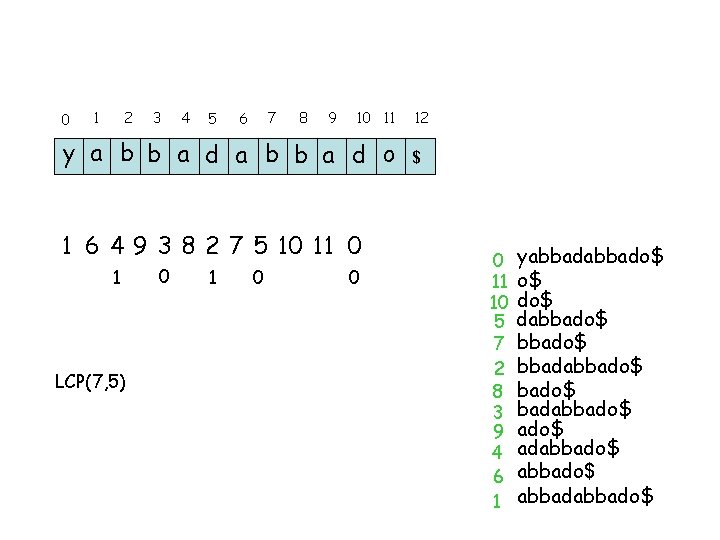
0 1 2 3 4 5 7 6 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 1 LCP(7, 5) 0 1 0 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

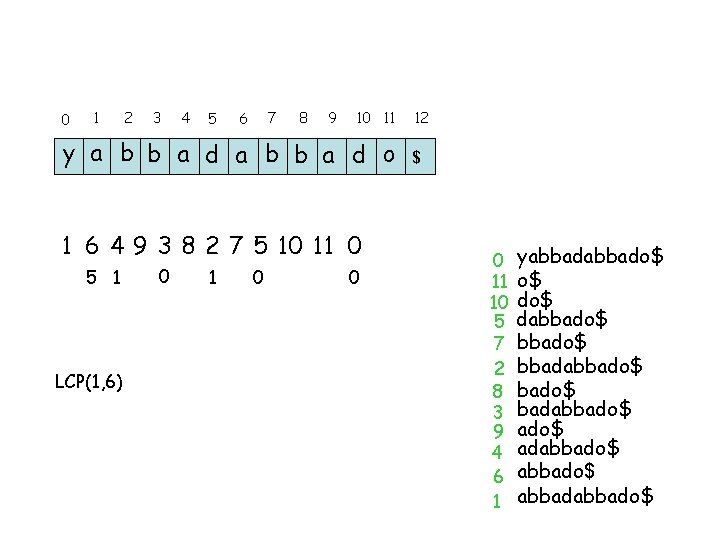
0 1 2 3 4 5 7 6 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 5 1 LCP(1, 6) 0 1 0 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

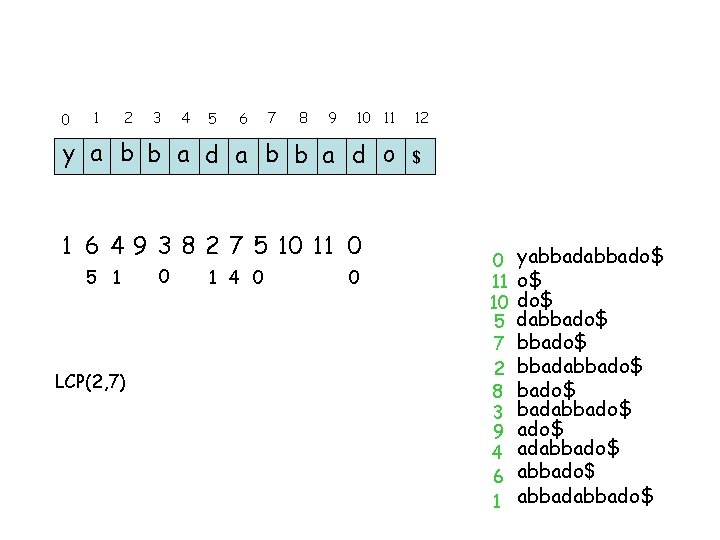
0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 5 1 LCP(2, 7) 0 1 4 0 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

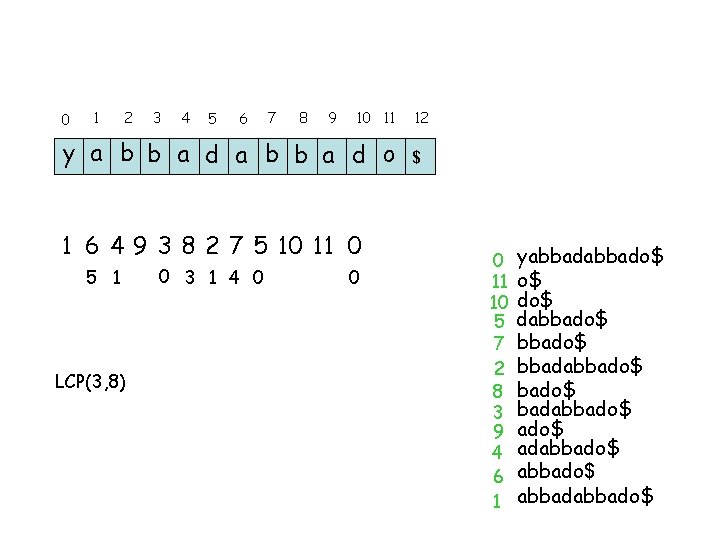
0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 5 1 LCP(3, 8) 0 3 1 4 0 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

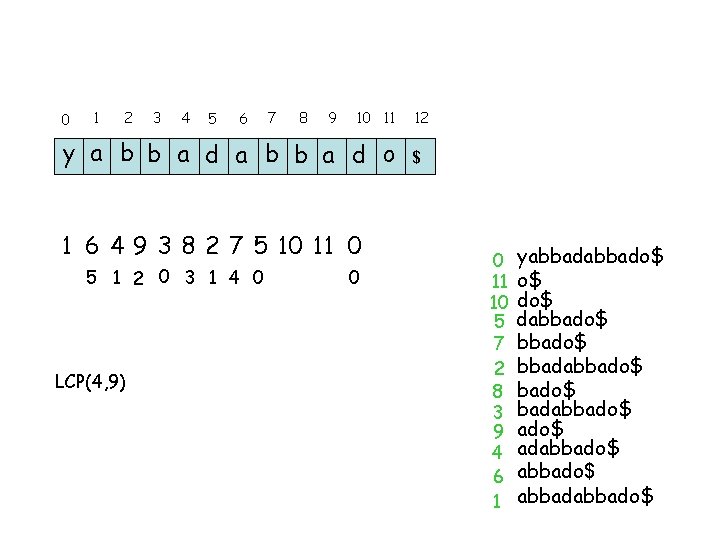
0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 5 1 2 0 3 1 4 0 LCP(4, 9) 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

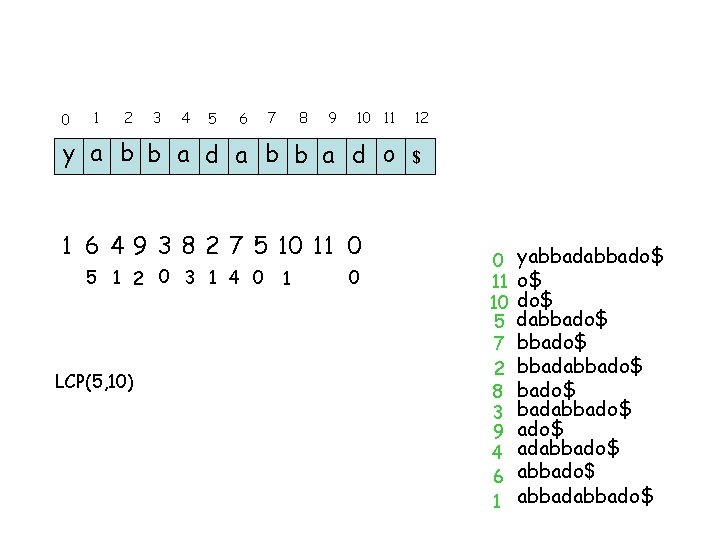
0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 5 1 2 0 3 1 4 0 LCP(5, 10) 1 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 1 6 4 9 3 8 2 7 5 10 11 0 5 1 2 0 3 1 4 0 LCP(10, 11) 1 0 0 12 $ 0 11 10 5 7 2 8 3 9 4 6 1 yabbado$ o$ dabbado$ bbadabbado$ adabbado$

We need more LCPs for search 0 1 2 3 4 5 6 7 8 9 10 11 y a b b a d o 12 $ 1 6 4 9 3 8 2 7 5 10 11 0 5 1 2 0 3 1 4 0 1 0 0 Linearly many, calculate the all bottom up

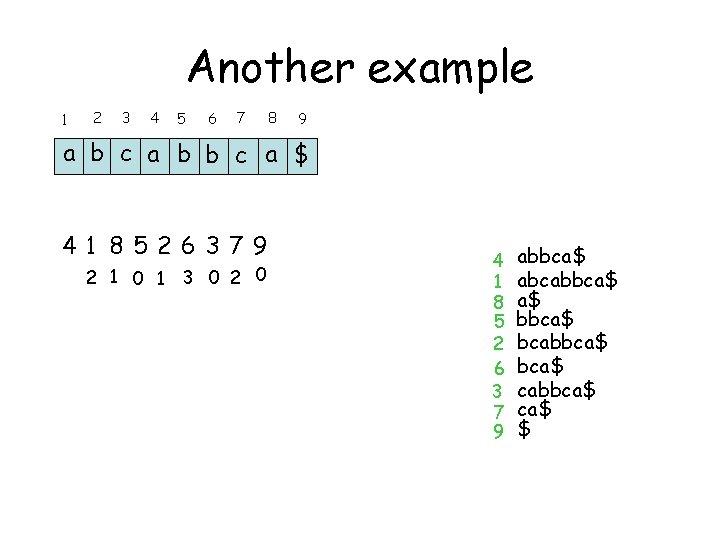
Another example 1 2 3 4 5 6 7 8 9 a b c a b b c a $ 41 8526379 2 1 0 1 3 0 2 0 4 1 8 5 2 6 3 7 9 abbca$ abcabbca$ a$ bbca$ cabbca$ $

Burrows –Wheeler (bzip 2) Currently best algorithm for text High level: • Apply the Borrows-Wheeler transform • Use move-to-front to translate the sorted characters to small integers • Use Huffman coding


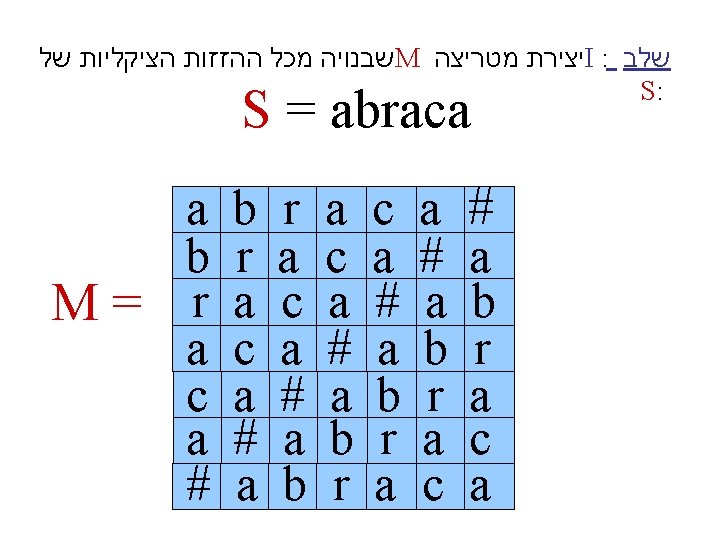
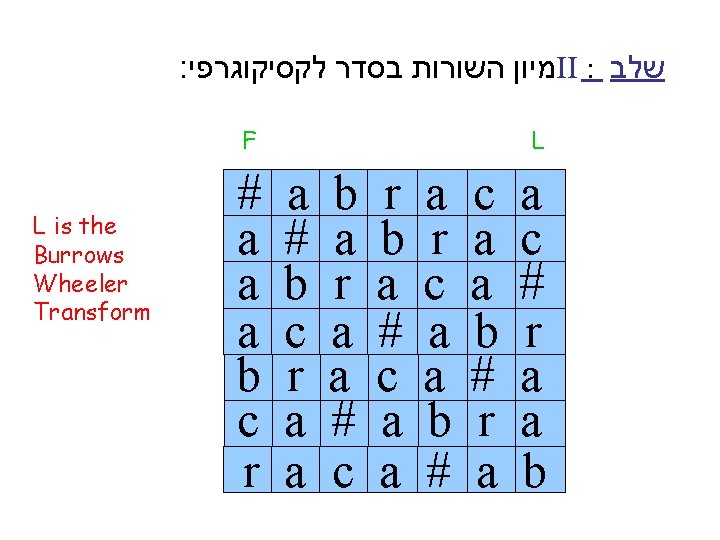
: מיון השורות בסדר לקסיקוגרפי II : שלב F L is the Burrows Wheeler Transform # a a a b c r L a # b c r a a b a r a a # c r b a # c a a a r c a a b # r a a c # r a a b

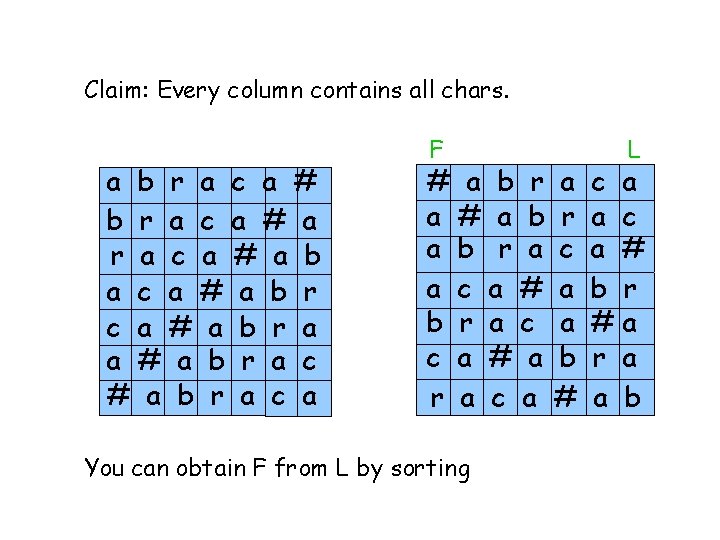
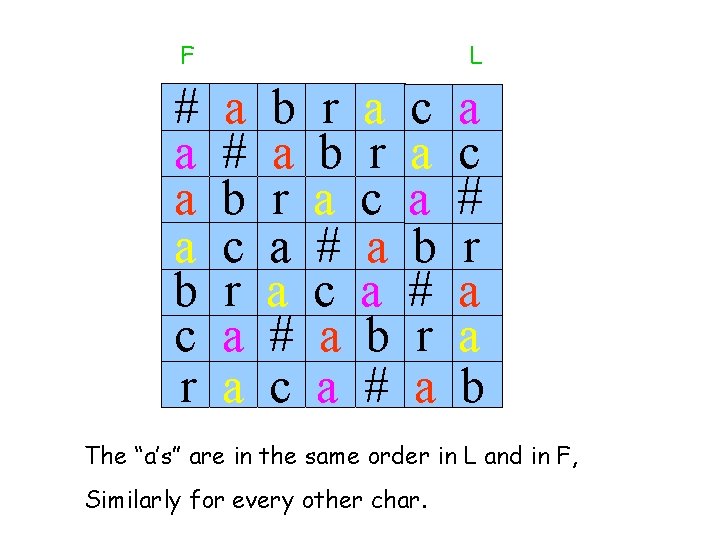
Claim: Every column contains all chars. a b r a c a # a b r c a # a b r a c a F # a b r a a c a # b r a c c a # a r a c a You can obtain F from L by sorting a r c a a b # L c a a c a # b r #a r a a b

F # a a a b c r L a # b c r a a b a r a a # c r b a # c a a a r c a a b # r a a c # r a a b The “a’s” are in the same order in L and in F, Similarly for every other char.

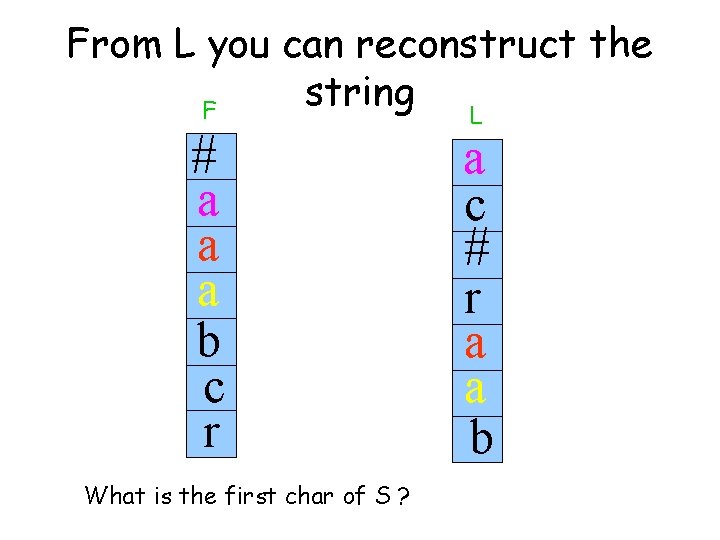
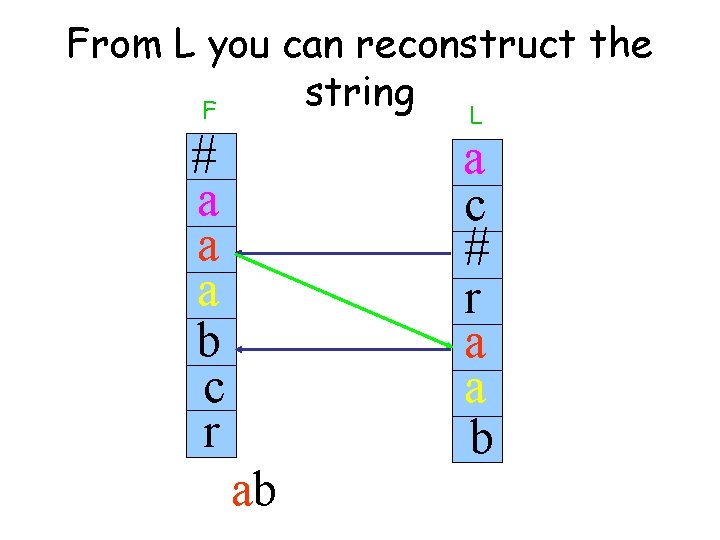
From L you can reconstruct the string L F # a a a b c r What is the first char of S ? a c # r a a b

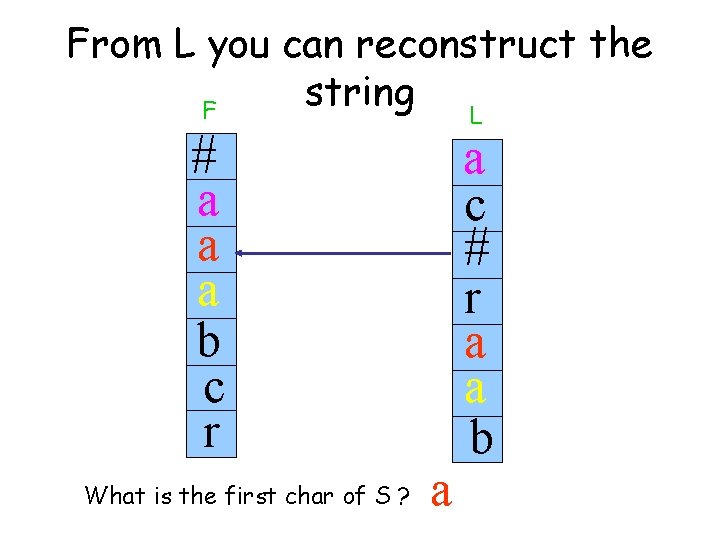
From L you can reconstruct the string L F # a c a a a b c r What is the first char of S ? # a r a a b

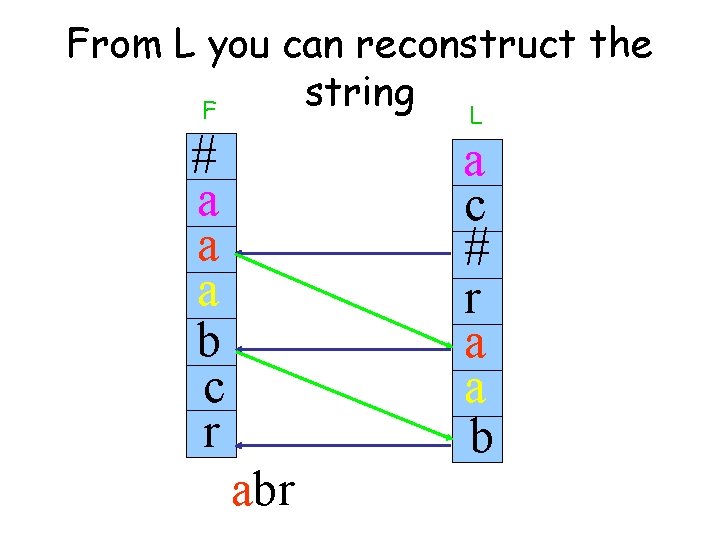
From L you can reconstruct the string L F # a c a a a b c r # ab r a a b

From L you can reconstruct the string L F # a c a a a b c r # abr r a a b

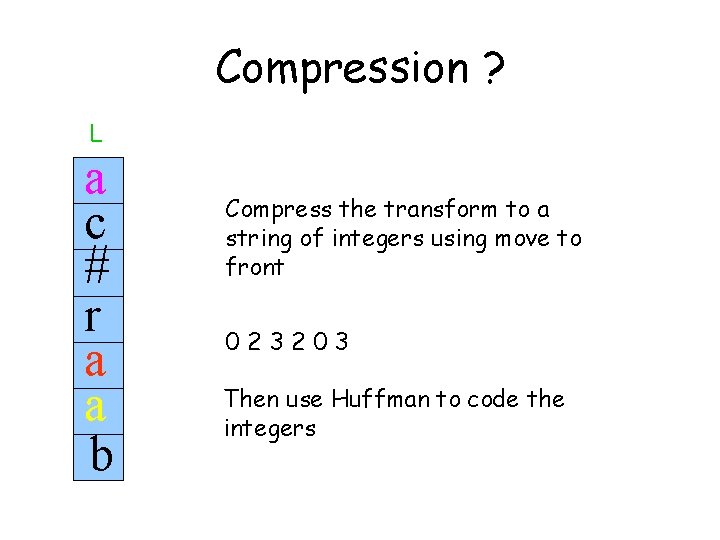
Compression ? L a c # r a a b Compress the transform to a string of integers using move to front 023203 Then use Huffman to code the integers

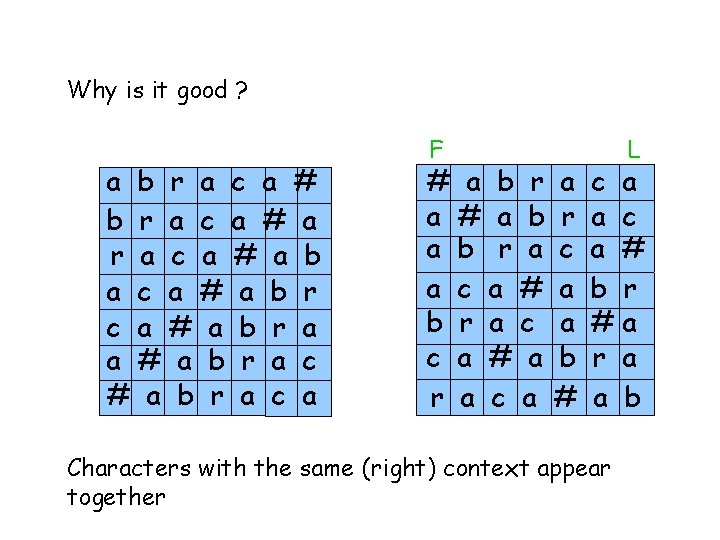
Why is it good ? a b r a c a # a b r c a # a b r a c a F # a b r a a c a # b r a c c a # a r a c a a r c a a b # L c a a c a # b r #a r a a b Characters with the same (right) context appear together

Sorting is equivalent to computing the suffix array. a b r a c a # a b r c a # a b r a c a F # a b r a a c a # b r a c c a # a r a c a Can encode and decode in linear time a r c a a b # L c a a c a # b r #a r a a b
![Substring search using the BWT P j Count the pattern occurrences C P Substring search using the BWT P[ j ] (Count the pattern occurrences) C P](https://slidetodoc.com/presentation_image_h2/a9b6189774c2fbee99074d279f18a555/image-63.jpg)
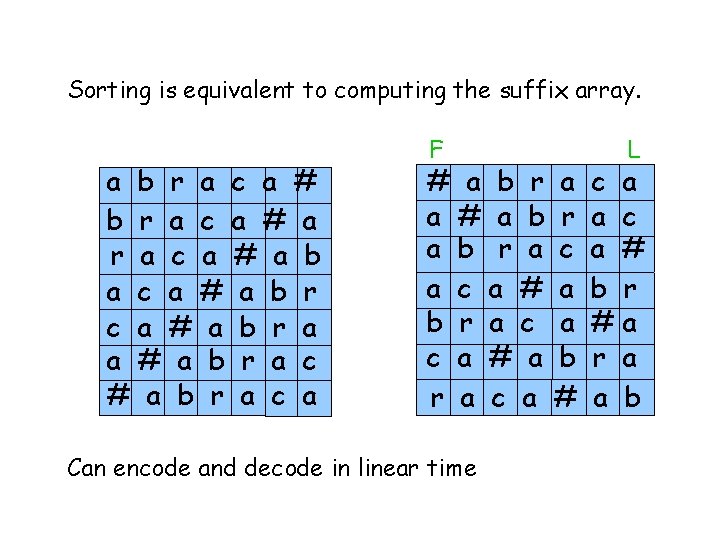
Substring search using the BWT P[ j ] (Count the pattern occurrences) C P = si First step rows prefixed by char “i” fr lr occ=2 [lr-fr+1] fr lr #mississipp i#mississip ippi#missis issippi#mis ississippi# mississippi pi#mississi ppi#mississ sippi#missi sissippi#miss ssissippi#m slide stolen from Paolo Ferragina@ L i p s s m # p i s s i i ai Av le b la fo in # i m p s 1 2 6 7 9 Inductive step: Given fr, lr for P[j+1, p] Take c=P[j] Find the first c in L[fr, lr] Find the last c in L[fr, lr] L-to-F mapping of these chars

Substring search using the BWT (Count the pattern occurrences) C P = si First step rows prefixed by char “i” fr lr occ=2 [lr-fr+1] fr lr #mississipp i#mississip ippi#missis issippi#mis ississippi# mississippi pi#mississi ppi#mississ sippi#missi sissippi#miss ssissippi#m slide stolen from Paolo Ferragina@ L i p s s m # p i s s i i ai Av le b la fo in # i m p s 1 2 6 7 9 What if someone whispers how many “s” we have up to index 2 and up to index 5: occ(s, 2), occ(s, 5) ? fr = C[s] + occ(s, 2) + 1 lr = C[s] + occ(s, 5)

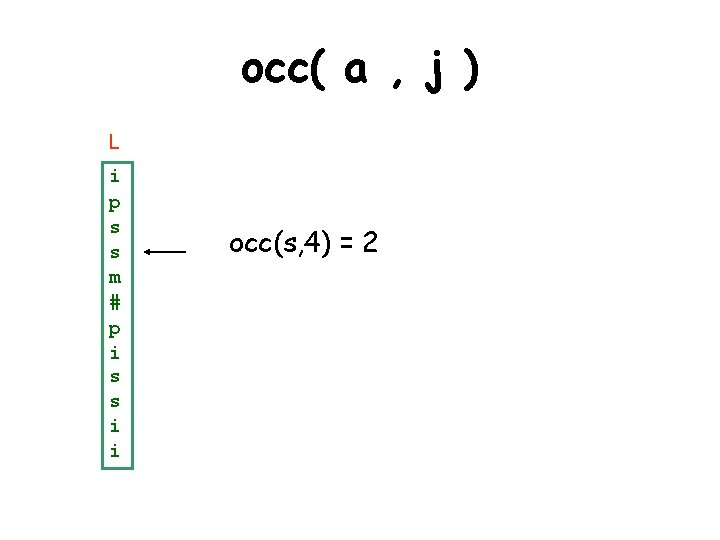
occ( a , j ) L i p s s m # p i s s i i occ(s, 4) = 2

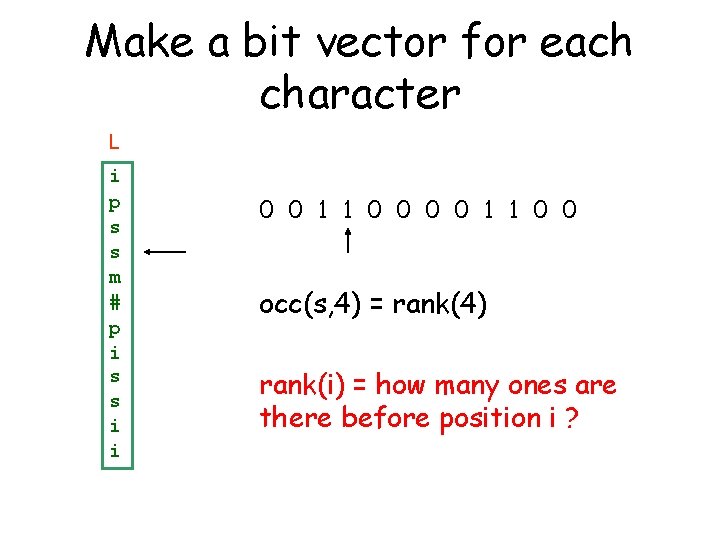
Make a bit vector for each character L i p s s m # p i s s i i 0 0 1 1 0 0 occ(s, 4) = rank(4) rank(i) = how many ones are there before position i ?

How do you answer rank queries ? 0 0 1 1 0 0 rank(i) = how many ones are there before position i ? We can prepare a vector with all answers 0 0 1 2 2 2 3 4 4 4

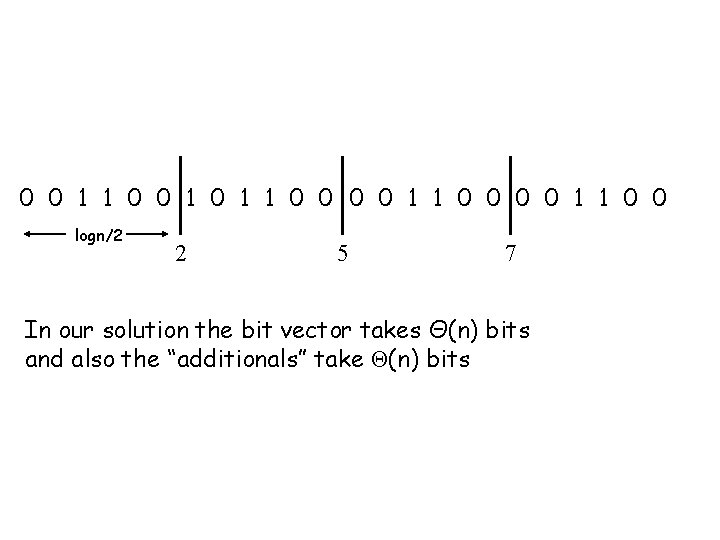
Lets do it with O(n) bits per character 0 0 1 1 0 0 0 0 1 1 0 0 logn/2 2 5 7 Partition in 2 n/log(n) blocks of size log(n)/2 Keep the answer for each prefix of the blocks There are “kinds” of blocks, prepare a table with all answers for each block

0 0 1 1 0 0 0 0 1 1 0 0 logn/2 2 5 7 In our solution the bit vector takes Θ(n) bits and also the “additionals” take Θ(n) bits

Can we do it with smaller overhead : so additionals would take o(n) ? 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 log 2 n 7 2 4 superblocks of size log 2(n) Each block keeps the number of one in previous blocks that are in the same superblock 13

Analysis 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 log 2 n 7 2 The superblock table is of size n/log (n) The block table is of size (loglog(n)) * n/log (n) The tables for the blocks √n log(n)loglog(n) So the additionals take o(n) space 4 13

Next step Do it without keeping the bit vectors themselves Instead keep only the compressed version of the text Saves a lot of space for compressible strings