Sudaryatno Sudirham Matematika II 1 ISI Turunan FungsiFungsi

Sudaryatno Sudirham Matematika II 1

ISI Turunan Fungsi-Fungsi: • Fungsi Polinom • Perkalian Fungsi, Pangkat dari Fungsi, Fungsi Rasional, Fungsi Implisit • Fungsi Trigonometri, Trigonometri Inversi, Logaritmik, Eksponensial Integral: • Integral Tak-Tentu • Integral Tentu Persamaan Diferensial • Persamaan Diferensial Orde-1 • Persamaan Diferensial Orde-2 2

Turunan Fungsi-Fungsi 3

Pengertian-Pengertian y Kita telah melihat bahwa kemiringan garis lurus adalah 2 Δy 1 Δx 0 0 1 2 3 4 x -1 Bagaimanakah dengan garis lengkung? 4

Garis Lengkung y = f(x) P 2 y Garis lurus dengan kemiringan y/ x memotong garis lengkung di dua titik Δy P 1 Δx Jarak kedua titik potong semakin kecil jika Δx di perkecil menjadi x* x y = f(x) y Pada kondisi Δx mendekati nol, kita peroleh Δy* P 1 Δx* x Ini merupakan fungsi turunan dari di titik P Ekivalen dengan kemiringan garis singgung di titik P 5

y (x 2, y 2) (x 1, y 1) x Pada suatu garis lengkung kita dapat memperoleh turunannya di berbagai titik pada garis lengkung tersebut f ′(x) di titik (x 1, y 1) adalah turunan y di titik (x 1, y 1), f ′(x) di titik (x 2, y 2) adalah turunan y di titik (x 2, y 2) 6

Jika pada suatu titik x 1 di mana benar ada maka dikatakan bahwa fungsi f(x) “dapat didiferensiasi di titik tersebut” Jika dalam suatu domain suatu fungsi f(x) dapat di-diferensiasi di semua x dalam domain tersebut kita katakan bahwa fungsi f(x) dapat di-diferensiasi dalam domain. kita baca “turunan fungsi y terhadap x” Penurunan ini dapat dilakukan jika y memang merupakan fungsi x. Jika tidak, tentulah penurunan itu tidak dapat dilakukan. 7

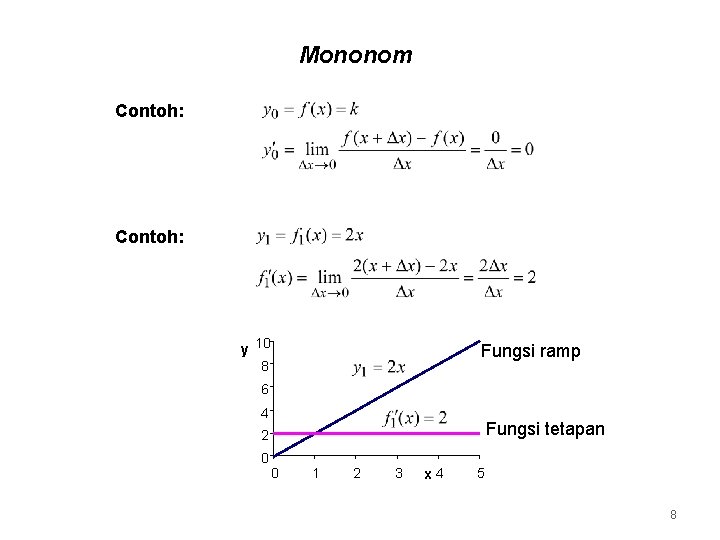
Mononom Contoh: y 10 8 Fungsi ramp 6 4 Fungsi tetapan 2 0 0 1 2 3 x 4 5 8

Contoh: Turunan fungsi mononom pangkat 2 berbentuk mononom pangkat 1 (kurva garis lurus) Contoh: Turunan fungsi mononom pangkat 3 berbentuk mononom pangkat 2 (kurva parabola) 9

Secara umum, turunan fungsi mononom adalah Jika n = 1 maka kurva fungsi berbentuk garis lurus *) dan turunannya berupa nilai konstan, Jika n > 1, maka turunan fungsi x, akan merupakan Fungsi turunan ini dapat diturunkan lagi dan kita mendapatkan fungsi turunan berikutnya, yang mungkin masih dapat diturunkan lagi turunan dari *) Untuk n berupa bilangan tak bulat akan dibahas kemudian 10

disebut turunan pertama, turunan kedua, turunan ke-tiga, dst. Contoh: 11

Kurva fungsi mononom yang memiliki beberapa turunan akan berpotongan dengan kurva fungsi-fungsi turunannya. Contoh: dan turunan-turunannya Fungsi 200 100 0 -3 -2 -1 0 1 2 3 4 -100 12

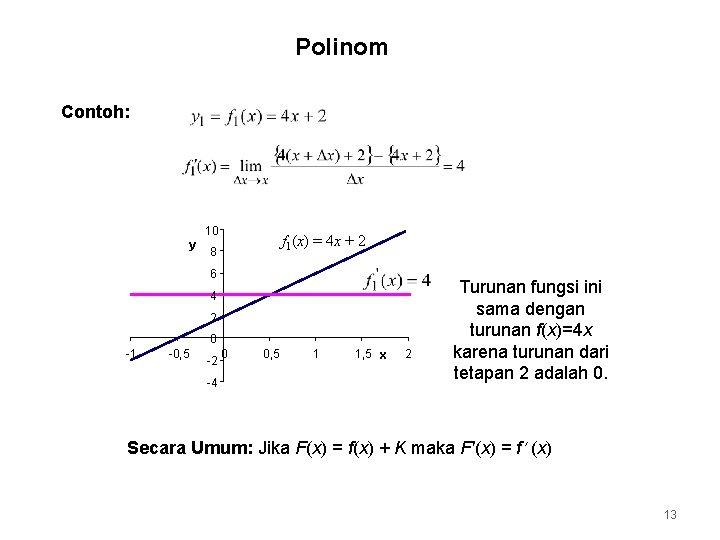
Polinom Contoh: 10 y f 1(x) = 4 x + 2 8 6 4 2 0 -1 -0, 5 -2 -4 0 0, 5 1 1, 5 x 2 Turunan fungsi ini sama dengan turunan f(x)=4 x karena turunan dari tetapan 2 adalah 0. Secara Umum: Jika F(x) = f(x) + K maka Fʹ(x) = f (x) 13

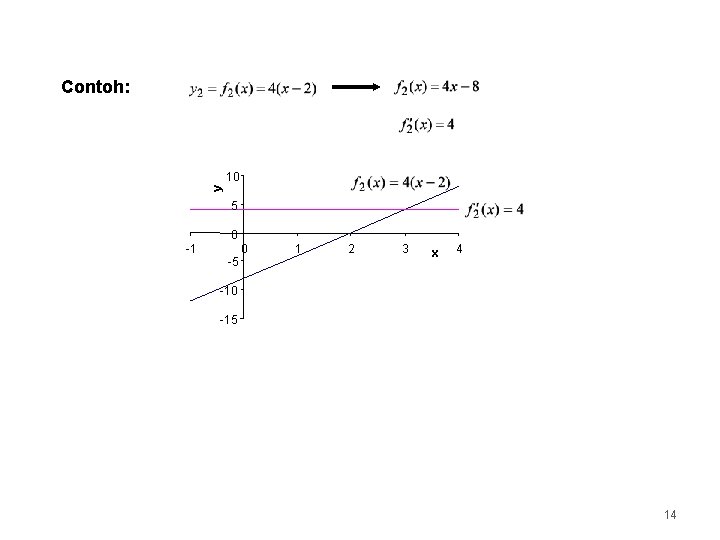
Contoh: y 10 5 0 -1 0 -5 1 2 3 x 4 -10 -15 14

Contoh: Secara Umum: Turunan fungsi polinom, yang merupakan jumlah beberapa mononom, adalah jumlah turunan masing-masing mononom dengan syarat setiap mononom yang membentuk polinom itu memang memiliki turunan. 15

Fungsi Yang Merupakan Perkalian Dua Fungsi Jika maka 16

Contoh: Turunan adalah Jika dipandang sebagai perkalian dua fungsi Jika Contoh: Jika dipandang sebagai perkalian tiga fungsi 17

Fungsi Yang Merupakan Pangkat dari suatu Fungsi Contoh: Contoh ini menunjukkan bahwa Secara Umum: 18

Contoh: Kita gabungkan relasi turunan untuk perkalian dua fungsi dan pangkat suatu fungsi 19

Fungsi Rasional Fungsi rasional merupakan rasio dari dua fungsi atau Jadi: 20

Contoh: (agar penyebut tidak nol) 21

Fungsi Berpangkat Tidak Bulat Bilangan tidak bulat dengan p dan q adalah bilangan bulat dan q ≠ 0 (v adalah fungsi yang bisa diturunkan) Jika y ≠ 0, kita dapatkan sehingga Formulasi ini mirip dengan keadaan jika n bulat, hanya perlu persyaratan bahwa v ≠ 0 untuk p/q < 1. 22

Fungsi Parametrik dan Kaidah Rantai Apabila kita mempunyai persamaan maka relasi antara x dan y dapat dinyatakan dalam t. Persamaan demikian disebut persamaan parametrik, dan t disebut parameter. Jika kita eliminasi t dari kedua persamaan di atas, kita dapatkan persamaan yang berbentuk Kaidah rantai Jika maka dapat diturunkan terhadap x dan dapat diturunkan terhadap t, dapat diturunkan terhadap t menjadi 23

Fungsi Implisit Sebagian fungsi implisit dapat diubah ke dalam bentuk explisit namun sebagian yang lain tidak. Untuk fungsi yang dapat diubah dalam bentuk eksplisit, turunan fungsi dapat dicari dengan cara seperti yang sudah kita pelajari di atas. Untuk mencari turunan fungsi yang tak dapat diubah ke dalam bentuk eksplisit perlu cara khusus, yang disebut diferensiasi implisit. Dalam cara ini kita menganggap bahwa fungsi y dapat didiferensiasi terhadap x. 24

Contoh: Fungsi implisit ini merupakan sebuah persamaan. Jika kita melakukan operasi matematis di ruas kiri, maka operasi yang sama harus dilakukan pula di ruas kanan agar kesamaan tetap terjaga. Kita lakukan diferensiasi (cari turunan) di kedua ruas, dan kita akan peroleh Jika kita peroleh turunan 25

Contoh: Fungsi implisit ini juga merupakan sebuah persamaan. Kita lakukan diferensiasi pada kedua ruas, dan kita akan memperoleh Untuk kita dapat memperoleh turunan 26

Turunan Fungsi Trigonometri Jika maka Untuk nilai yang kecil, Δx menuju nol, cos x = 1 dan sin x = x. Oleh karena itu 27

Jika maka Untuk nilai yang kecil, Δx menuju nol, cos x = 1 dan sin x = x. Oleh karena itu 28

Turunan fungsi trigonometri yang lain tidak terlalu sulit untuk dicari. 29

Contoh: Hubungan antara tegangan kapasitor v. C dan arus kapasitor i. C adalah Tegangan pada suatu kapasitor dengan kapasitansi C = 2 10 -6 farad merupakan fungsi sinus v. C = 200 sin 400 t volt. Arus yang mengalir pada kapasitor ini adalah v. C i. C 200 i. C 100 0 -100 0 0. 01 0. 02 0. 03 0. 04 0. 05 t [detik] -200 30

Contoh: Arus pada suatu inductor L = 2, 5 henry merupakan fungsi sinus i. L = 0, 2 cos 400 t ampere. Hubungan antara tegangan induktor v. L dan arus induktor i. L adalah v. L i. L 200 100 0 -100 0 0. 01 0. 02 0. 03 0. 04 0. 05 t[detik] -200 31

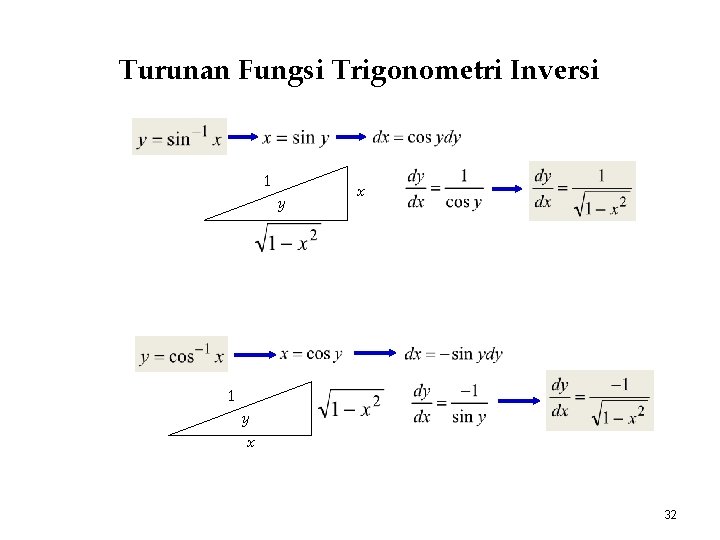
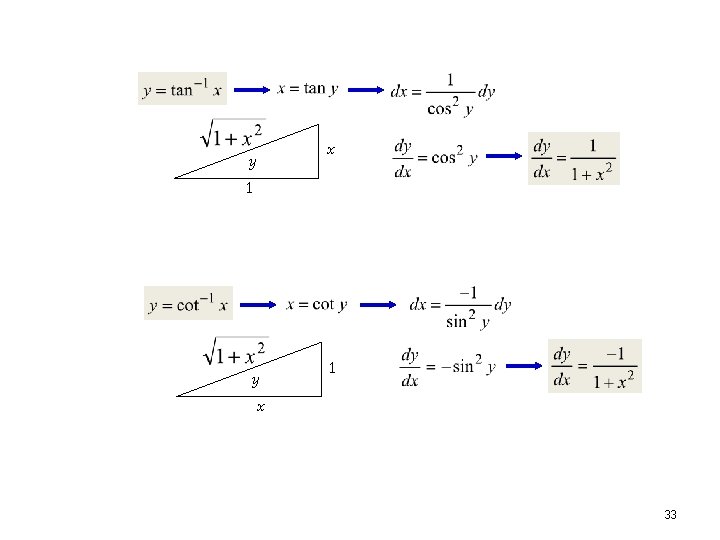
Turunan Fungsi Trigonometri Inversi 1 y x 32

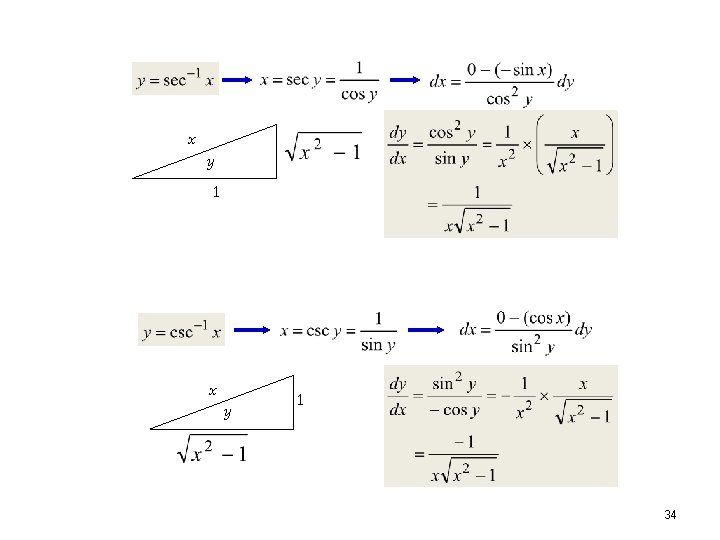
y x 1 y 1 x 33

x y 1 34

Fungsi Trigonometri dari Suatu Fungsi Jika v = f(x), maka 35

Jika w = f(x), maka 36

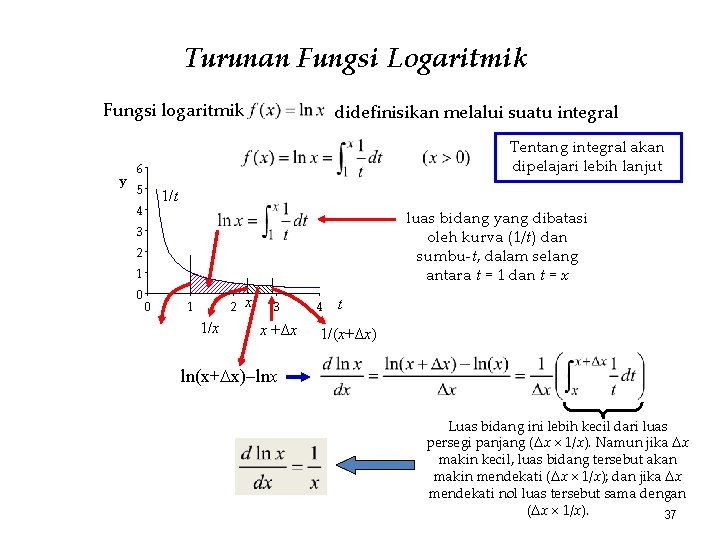
Turunan Fungsi Logaritmik Fungsi logaritmik y didefinisikan melalui suatu integral Tentang integral akan dipelajari lebih lanjut 6 5 1/t 4 luas bidang yang dibatasi oleh kurva (1/t) dan sumbu-t, dalam selang antara t = 1 dan t = x 3 2 1 0 0 1 2 1/x x 3 x +Δx 4 t 1/(x+Δx) ln(x+ x) lnx Luas bidang ini lebih kecil dari luas persegi panjang (Δx 1/x). Namun jika Δx makin kecil, luas bidang tersebut akan makin mendekati (Δx 1/x); dan jika Δx mendekati nol luas tersebut sama dengan (Δx 1/x). 37

Turunan Fungsi Eksponensial penurunan secara implisit di kedua sisi atau . Jadi turunan dari ex adalah ex itu sendiri dst. Jika 38

Diferensial dx dan dy Turunan fungsi y(x) terhadap x dinyatakan dengan formulasi Sekarang kita akan melihat dx dan dy yang didefinisikan sedemikian rupa sehingga rasio dy/dx , jika dx 0, sama dengan turunan fungsi y terhadap x. Hal ini mudah dilakukan jika x adalah peubah bebas dan y merupakan fungsi dari x: dx dan dy didefinisikan sebagai berikut: 1). dx, yang disebut sebagai diferensial x, adalah bilangan nyata dan merupakan peubah bebas lain selain x; 2). dy, yang disebut sebagai diferensial y, adalah fungsi dari x dan dx yang dinyatakan dengan 39

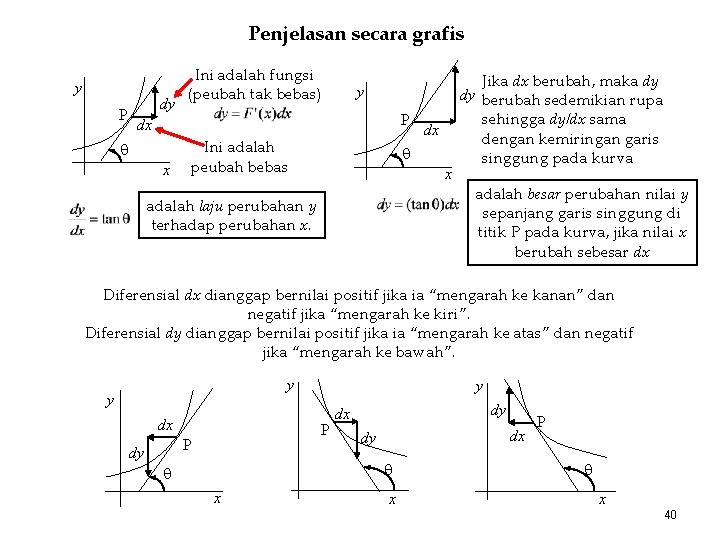
Penjelasan secara grafis y P dy Ini adalah fungsi (peubah tak bebas) y P dx x Ini adalah peubah bebas dx x adalah laju perubahan y terhadap perubahan x. Jika dx berubah, maka dy dy berubah sedemikian rupa sehingga dy/dx sama dengan kemiringan garis singgung pada kurva adalah besar perubahan nilai y sepanjang garis singgung di titik P pada kurva, jika nilai x berubah sebesar dx Diferensial dx dianggap bernilai positif jika ia “mengarah ke kanan” dan negatif jika “mengarah ke kiri”. Diferensial dy dianggap bernilai positif jika ia “mengarah ke atas” dan negatif jika “mengarah ke bawah”. y y dx P P dy y dy dx dx dy x x P x 40

Dengan pengertian diferensial seperti di atas, kita kumpulkan formula turunan fungsi dan formula diferensial fungsi dalam tabel berikut. Dalam tabel ini v adalah fungsi x. Turunan Fungsi Diferensial 41

Ada dua cara untuk mencari diferensial suatu fungsi. 1). Mencari turunannya lebih dulu (kolom kiri tabel), kemudian dikalikan dengan dx. 2). Menggunakan langsung formula diferensial (kolom kanan tabel) Contoh: sehingga Kita dapat pula mencari langsung dengan menggunakan formula dalam tabel di atas 42

Integral 43

1. Integral Tak Tentu Pengertian-Pengertian Misalkan dari suatu fungsi f(x) yang diketahui, kita diminta untuk mencari suatu fungsi y sedemikian rupa sehingga dalam rentang nilai x tertentu, misalnya a< x < b, dipenuhi persamaan Persamaan yang menyatakan turunan fungsi sebagai fungsi x seperti ini disebut persamaan diferensial. Contoh persamaan diferensial 44

Tinjau persamaan diferensial Suatu fungsi dikatakan merupakan solusi dari persamaan diferensial jika dalam rentang tertentu ia dapat diturunkan dapat memenuhi Karena fungsi maka juga merupakan solusi 45

dapat dituliskan Integrasi ruas kiri dan ruas kanan memberikan secara umum Jadi integral dari diferensial suatu fungsi adalah fungsi itu sendiri ditambah suatu nilai tetapan. Integral semacam ini disebut integral tak tentu di mana masih ada nilai tetapan K yang harus dicari 46

Contoh: Cari solusi persamaan diferensial ubah ke dalam bentuk diferensial Kita tahu bahwa oleh karena itu 47

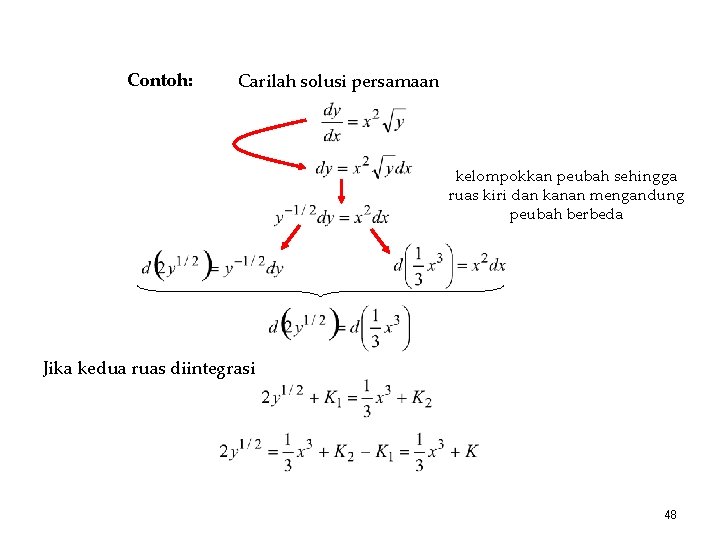
Contoh: Carilah solusi persamaan kelompokkan peubah sehingga ruas kiri dan kanan mengandung peubah berbeda Jika kedua ruas diintegrasi 48

Dalam proses integrasi seperti di atas terasa adanya keharusan untuk memiliki kemampuan menduga jawaban. Beberapa hal tersebut di bawah ini dapat memperingan upaya pendugaan tersebut. 1. Integral dari suatu diferensial dy adalah y ditambah konstanta K. 2. Suatu konstanta yang berada di dalam tanda integral dapat dikeluarkan 3. Jika bilangan n 1, maka integral dari yndy diperoleh dengan menambah pangkat n dengan 1 menjadi (n + 1) dan membaginya dengan (n + 1). 49

Penggunaan Integral Tak Tentu Dalam integral tak tentu, terdapat suatu nilai K yang merupakan bilangan nyata sembarang. Ini berarti bahwa integral tak tentu memberikan hasil yang tidak tunggal melainkan banyak hasil yang tergantung dari berapa nilai yang dimiliki oleh K. yi = 10 x 2 +Ki y = 10 x 2 100 y -3 -1 K 3 K 2 K 1 50 50 -5 y 1 3 x 5 kurva adalah kurva bernilai tunggal -5 -3 -1 1 3 x 5 kurva adalah kurva bernilai banyak 50

Dalam pemanfaatan integral tak tentu, nilai K diperoleh dengan menerapkan apa yang disebut sebagai syarat awal atau kondisi awal. Contoh: Kecepatan sebuah benda bergerak dinyatakan sebagai kecepatan percepatan waktu Posisi benda pada waktu t = 0 adalah benda pada t = 4. ; tentukanlah posisi Kecepatan adalah laju perubahan jarak, Percepatan adalah laju perubahan kecepatan, . Kondisi awal: pada t = 0, s 0 = 3 sehingga pada t = 4 posisi benda adalah 51

Luas Sebagai Suatu Integral Kita akan mencari luas bidang yang dibatasi oleh suatu kurva sumbu-x, garis vertikal x = p, dan x = q. Contoh: y Apx 2 0 p x y = f(x) =2 x+ x q x atau Kondisi awal (kondisi batas) adalah Apx = 0 untuk x = p atau 52

Kasus fungsi sembarang dengan syarat kontinyu dalam rentang y f(x+ x ) f(x) 0 p x y = f(x) x+ x q x Apx bisa memiliki dua nilai tergantung dari pilihan Apx = f(x) x atau Apx = f(x+ x) x x 0 adalah suatu nilai x yang terletak antara x dan x+ x Jika x 0: 53

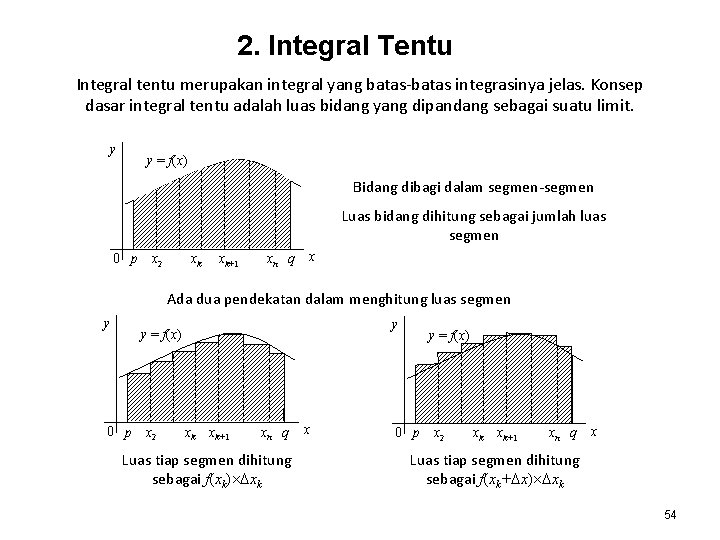
2. Integral Tentu Integral tentu merupakan integral yang batas-batas integrasinya jelas. Konsep dasar integral tentu adalah luas bidang yang dipandang sebagai suatu limit. y y = f(x) Bidang dibagi dalam segmen-segmen Luas bidang dihitung sebagai jumlah luas segmen 0 p x 2 xk xk+1 xn q x Ada dua pendekatan dalam menghitung luas segmen y y y = f(x) 0 p x 2 xk xk+1 xn q Luas tiap segmen dihitung sebagai f(xk) xk x y = f(x) 0 p x 2 xk xk+1 xn q x Luas tiap segmen dihitung sebagai f(xk+ x) xk 54

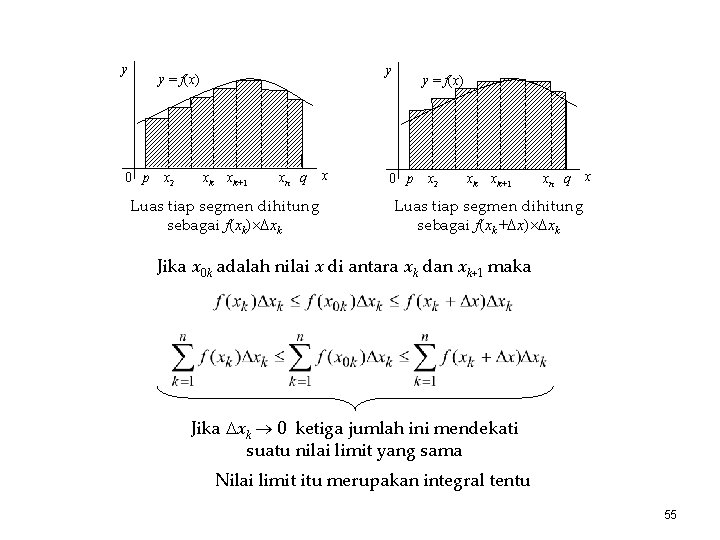
y y y = f(x) 0 p x 2 xk xk+1 xn q Luas tiap segmen dihitung sebagai f(xk) xk x y = f(x) 0 p x 2 xk xk+1 xn q x Luas tiap segmen dihitung sebagai f(xk+ x) xk Jika x 0 k adalah nilai x di antara xk dan xk+1 maka Jika xk 0 ketiga jumlah ini mendekati suatu nilai limit yang sama Nilai limit itu merupakan integral tentu 55

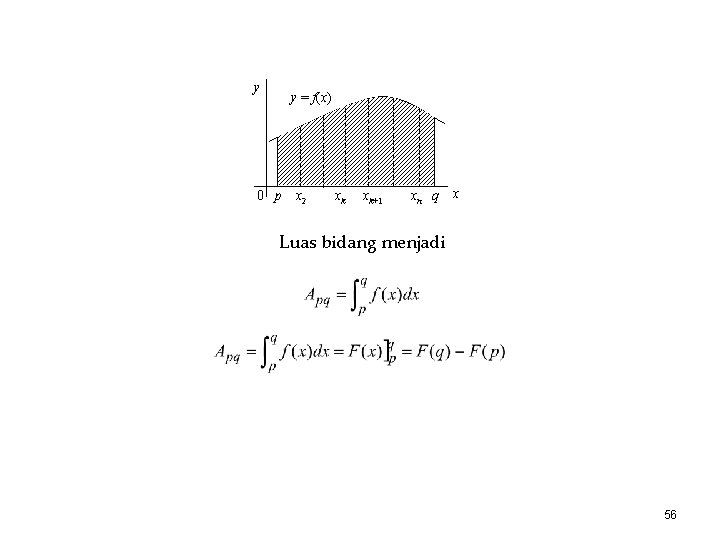
y y = f(x) 0 p x 2 xk xk+1 xn q x Luas bidang menjadi 56

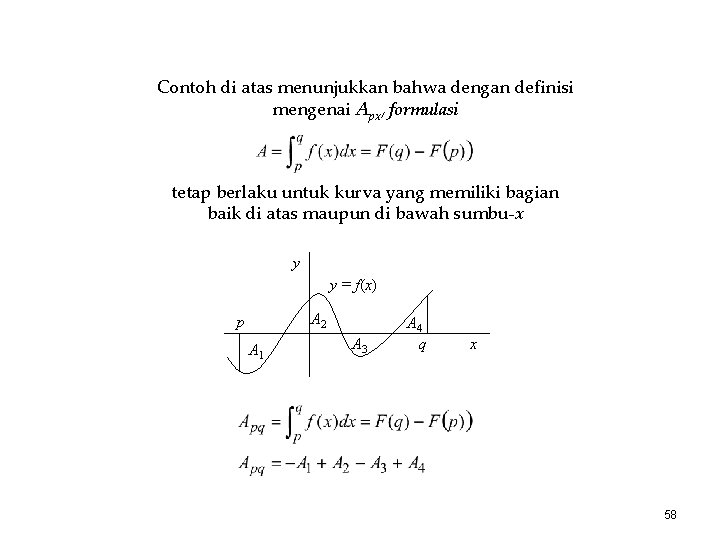
Luas Bidang Definisi Apx adalah luas bidang yang dibatasi oleh y=f(x) dan sumbu-x dari p sampai x, yang merupakan jumlah luas bagian yang berada di atas sumbu-x dikurangi dengan luas bagian yang di bawah sumbu-x. Luas antara dan sumbu-x dari x = 3 sampai x = +3. Contoh: 20 10 -4 -3 -2 0 -10 1 2 3 4 x -20 57

Contoh di atas menunjukkan bahwa dengan definisi mengenai Apx, formulasi tetap berlaku untuk kurva yang memiliki bagian baik di atas maupun di bawah sumbu-x y y = f(x) A 2 p A 1 A 3 A 4 q x 58

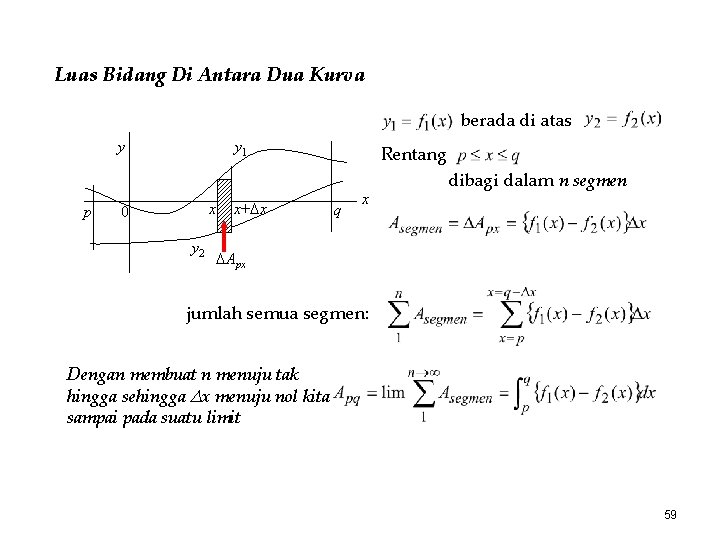
Luas Bidang Di Antara Dua Kurva berada di atas y p y 1 x 0 y 2 x+ x Rentang q x dibagi dalam n segmen Apx jumlah semua segmen: Dengan membuat n menuju tak hingga sehingga x menuju nol kita sampai pada suatu limit 59

Contoh: Jika dan berapakah luas bidang antara y 1 dan y 2 dari x 1 = p = 2 sampai x 2 = q = +3. Contoh: dan Jika berapakah luas bidang yang dibatasi oleh y 1 dan y 2. Terlebih dulu kita cari batas-batas integrasi yaitu nilai x pada perpotongan antara y 1 dan y 2 4 y y 1 -2 y 2 di atas x y 1 2 -1 0 0 1 2 60

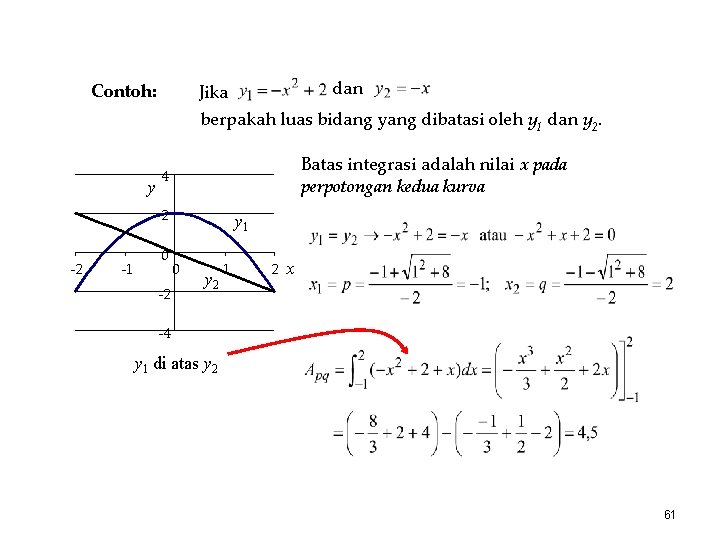
Contoh: dan Jika berpakah luas bidang yang dibatasi oleh y 1 dan y 2. y Batas integrasi adalah nilai x pada perpotongan kedua kurva 4 2 -2 -1 0 -2 y 1 0 y 2 1 2 x -4 y 1 di atas y 2 61

Penerapan Integral Contoh: Sebuah piranti menyerap daya 100 W pada tegangan konstan 200 V. Berapakah energi yang diserap oleh piranti ini selama 8 jam ? Daya adalah laju perubahan energi. Jika daya diberi simbol p dan energi diberi simbol w, maka yang memberikan Perhatikan bahwa peubah bebas di sini adalah waktu, t. Kalau batas bawah dari waktu kita buat 0, maka batasnya adalah 8, dengan satuan jam. Dengan demikian maka energi yang diserap selama 8 jam adalah 62

Contoh: Arus yang melalui suatu piranti berubah terhadap waktu sebagai i(t) = 0, 05 t ampere. Berapakah jumlah muatan yang dipindahkan melalui piranti ini antara t = 0 sampai t = 5 detik ? Arus i adalah laju perubahan transfer muatan, q. sehingga Jumlah muatan yang dipindahkan dalam 5 detik adalah 63

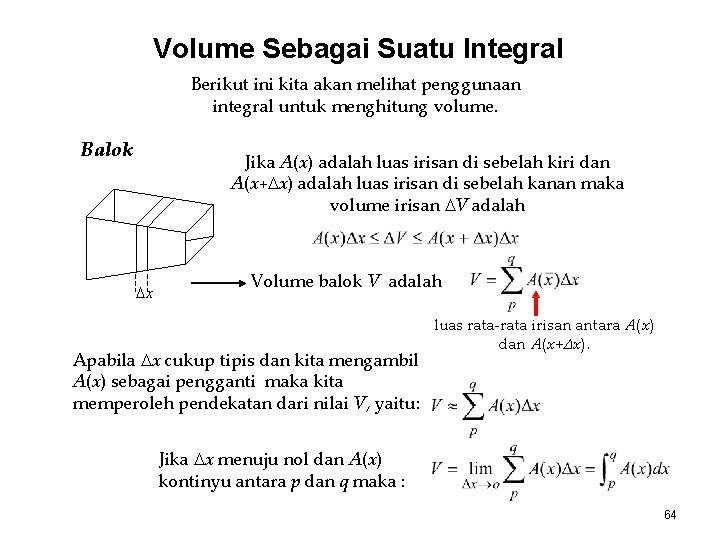
Volume Sebagai Suatu Integral Berikut ini kita akan melihat penggunaan integral untuk menghitung volume. Balok Jika A(x) adalah luas irisan di sebelah kiri dan A(x+ x) adalah luas irisan di sebelah kanan maka volume irisan V adalah x Volume balok V adalah Apabila x cukup tipis dan kita mengambil A(x) sebagai pengganti maka kita memperoleh pendekatan dari nilai V, yaitu: luas rata-rata irisan antara A(x) dan A(x+ x). Jika x menuju nol dan A(x) kontinyu antara p dan q maka : 64

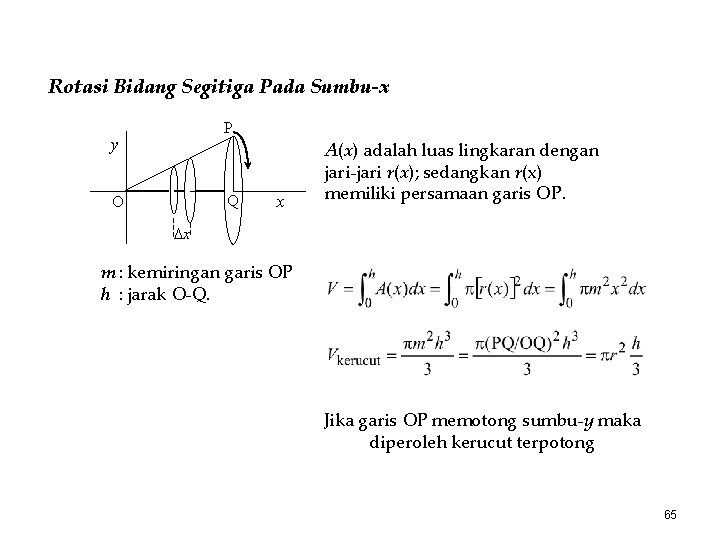
Rotasi Bidang Segitiga Pada Sumbu-x P y Q O x A(x) adalah luas lingkaran dengan jari-jari r(x); sedangkan r(x) memiliki persamaan garis OP. x m : kemiringan garis OP h : jarak O-Q. Jika garis OP memotong sumbu-y maka diperoleh kerucut terpotong 65

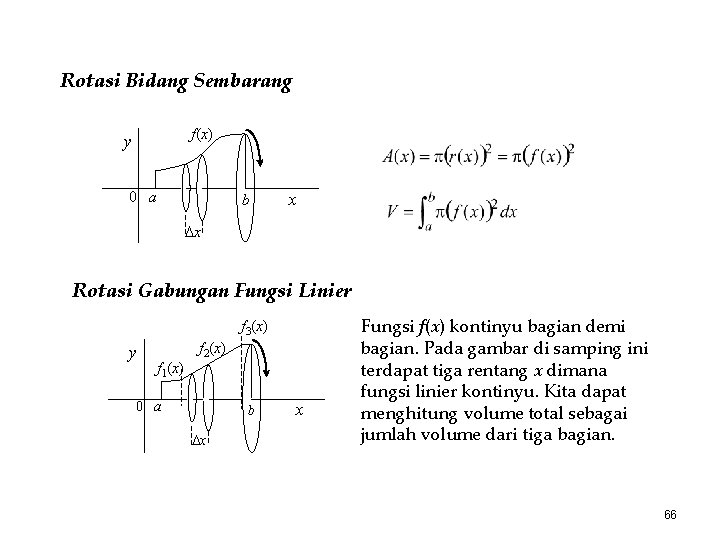
Rotasi Bidang Sembarang f(x) y 0 a b x x Rotasi Gabungan Fungsi Linier f 3(x) y f 1(x) f 2(x) 0 a b x x Fungsi f(x) kontinyu bagian demi bagian. Pada gambar di samping ini terdapat tiga rentang x dimana fungsi linier kontinyu. Kita dapat menghitung volume total sebagai jumlah volume dari tiga bagian. 66

Persamaan Diferensial 67

1. Persamaan Diferensial Orde-1 Pengertian Persamaan diferensial adalah suatu persamaan di mana terdapat satu atau lebih turunan fungsi. Persamaan diferensial diklasifikasikan sebagai berikut: 1. Menurut jenis atau tipe: ada persamaan diferensial biasa dan persamaan diferensial parsial. Jenis yang kedua tidak termasuk pembahasan di sini, karena kita hanya meninjau fungsi dengan satu peubah bebas. 2. Menurut orde: orde persamaan diferensial adalah orde tertinggi turunan fungsi yang ada dalam persamaan. 3. Menurut derajat: derajat suatu persamaan diferensial adalah pangkat tertinggi dari turunan fungsi orde tertinggi. Contoh: adalah persamaan diferensial biasa, orde tiga, derajat dua. 68

Solusi Suatu fungsi y = f(x) dikatakan merupakan solusi dari suatu persamaan diferensial jika persamaan tersebut tetap terpenuhi dengan digantikannya y dan turunannya dalam persamaan tersebut oleh f(x) dan turunannya. Contoh: adalah solusi dari persamaan karena turunan adalah dan jika ini kita masukkan dalam persamaan akan kita peroleh Persamaan terpenuhi. Pada umumnya suatu persamaan orde n akan memiliki solusi yang mengandung n tetapan sembarang. 69

Persamaan Diferensial Orde-1 Dengan Peubah Yang Dapat Dipisahkan Pemisahan Peubah Jika pemisahan peubah ini bisa dilakukan maka persamaan diferensial dapat kita tuliskan dalam bentuk Suku-suku terbentuk dari peubah yang berbeda Apabila kita lakukan integrasi, kita akan mendapatkan solusi umum dengan satu tetapan sembarang K, yaitu 70

Contoh: Persamaan ini dapat kita tuliskan yang kemudian dapat kita tuliskan sebagai persamaan dengan peubah terpisah Integrasi kedua ruas memberikan: atau sehingga Contoh: Pemisahan peubah akan memberikan bentuk atau Integrasi kedua ruas: atau 71

Persamaan Diferensial Homogen Orde Satu Suatu persamaan disebut homogen jika ia dapat dituliskan dalam bentuk Ini dapat dijadikan sebagai peubah bebas baru yang akan memberikan dan Pemisahan peubah: atau: 72

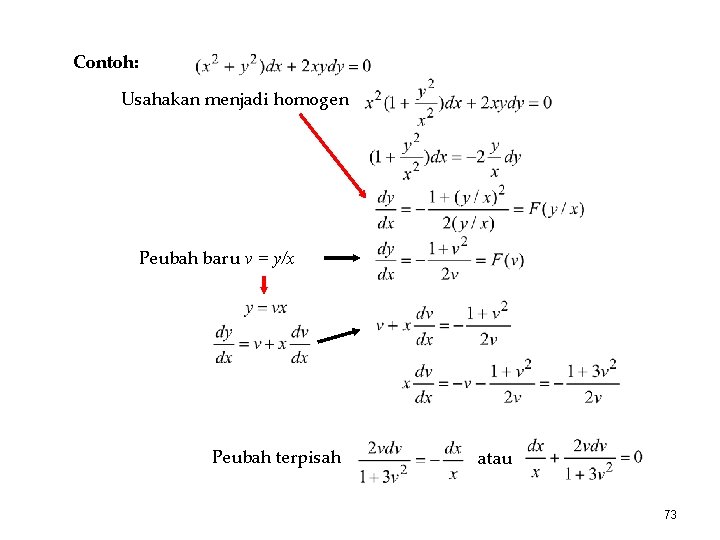
Contoh: Usahakan menjadi homogen Peubah baru v = y/x Peubah terpisah atau 73

Kita harus mencari solusi persamaan ini untuk mendapatkan v sebagai fungsi x. Suku ke-dua ini berbentuk 1/x dan kita tahu bahwa Kita coba hitung Hasil hitungan ini dapat digunakan untuk mengubah bentuk persamaan menjadi Integrasi ke-dua ruas: 74

Persamaan Diferensial Linier Orde Satu Dalam persamaan diferensial linier, semua suku berderajat satu atau nol Oleh karena itu persamaan diferensial orde satu yang juga linier dapat kita tuliskan dalam bentuk: P dan Q merupakan fungsi x atau tetapan Pembahasan akan dibatasi pada situasi dimana P adalah suatu tetapan. Hal ini kita lakukan karena pembahasan akan langsung dikaitkan dengan pemanfaatan praktis dalam analisis rangkaian listrik. Persamaan diferensial yang akan ditinjau dituliskan secara umum sebagai Dalam aplikasi pada analisis rangkaian listrik, f(t) tidak terlalu bervariasi. Mungkin ia bernilai 0, atau mempunyai bentuk sinyal utama yang hanya ada tiga, yaitu anak tangga, eksponensial, dan sinus. Kemungkinan lain adalah bahwa ia merupakan bentuk komposit yang merupakan gabungan dari bentuk utama. 75

Persamaan diferensial linier orde satu seperti ini biasa kita temui pada peristiwa transien (atau peristiwa peralihan) dalam rangkaian listrik. Cara yang akan kita gunakan untuk mencari solusi adalah cara pendugaan Peubah y adalah keluaran rangkaian (atau biasa disebut tanggapan rangkaian) yang dapat berupa tegangan ataupun arus sedangkan nilai a dan b ditentukan oleh nilai-nilai elemen yang membentuk rangkaian. Fungsi f(t) adalah masukan pada rangkaian yang dapat berupa tegangan ataupun arus dan disebut fungsi pemaksa atau fungsi penggerak. Persamaan diferensial linier mempunyai solusi total yang merupakan jumlah dari solusi khusus dan solusi homogen. Solusi khusus adalah fungsi yang dapat memenuhi persamaan yang diberikan, sedangkan solusi homogen adalah fungsi yang dapat memenuhi persamaan homogen 76

Hal ini dapat difahami karena jika f 1(t) memenuhi persamaan yang diberikan dan fungsi f 2(t) memenuhi persamaan homogen, maka y = (f 1+f 2) akan juga memenuhi persamaan yang diberikan, sebab Jadi y = (f 1+f 2) adalah solusi dari persamaan yang diberikan, dan kita sebut solusi total. Dengan kata lain solusi total adalah jumlah dari solusi khusus dan solusi homogen. 77

Solusi Homogen Persamaan homogen Jika ya adalah solusinya maka Integrasi kedua ruas memberikan sehingga Inilah solusi homogen 78

Jika solusi khusus adalah yp , maka Bentuk f(t) ini menentukan bagaimana bentuk yp. Dugaan bentuk-bentuk solusi yp yang tergantung dari f(t) ini dapat diperoleh karena hanya dengan bentuk-bentuk seperti itulah persamaan diferensial dapat dipenuhi Jika dugaan solusi total adalah Masih harus ditentukan melalui kondisi awal. 79

Contoh: Dari suatu analisis rangkaian diperoleh persamaan Carilah solusi total jika kondisi awal adalah v = 12 V. Persamaan ini merupakan persamaan homogen, f(t) = 0. Solusi khusus bernilai nol. Penerapan kondisi awal: Solusi total: 80

Contoh: Suatu analisis rangkaian memberikan persamaan Dengan kondisi awal v(0+) = 0 V , carilah tanggapan lengkap. Solusi homogen: Solusi khusus: karena f(t) = 12 Solusi total (dugaan): Penerapan kondisi awal: Solusi total: 81

Contoh: Pada kondisi awal v = 0 V, suatu analisis transien menghasilkan persamaan Carilah solusi total. Solusi homogen: Solusi khusus: Solusi total (dugaan): Penerapan kondisi awal: Solusi total : 82

Persamaan Diferensial Orde-2 Untuk sementara ini mengenai persamaan diferensial orde-2 silahkan dilihat Buku Analisis Rangkaian Listrik Jilid 2 83

Matematika II Sudaryatno Sudirham 84