Subtracting a proper fraction from a mixed number

$Subtracting a proper fraction from a mixed number fraction Success Criteria ü I can$

Subtracting a proper fraction from a mixed number fraction Success Criteria ü I can find the lowest common denominator ü I can identify a proper fraction ü I can subtract proper fractions from mixed number fractions DNA Complete this times table grid.

Retrieval practice Click on the speaker to hear Miss Odedina reading the retrieval questions 1 HP 2 HPs 3 HPs What is the lowest common multiple of 15 and 6? What is the product of 3 and 7? What is the lowest What is the product of common multiple of 3 9 and 7? and 6? What is the difference How many degrees is there in a full circle? between 500 cm and 1 km?

Retrieval practice 1 HP 2 HPs 3 HPs What is the lowest What is the product of common multiple of 3 and 7? 15 and 6? 21 30 What is the lowest What is the product of common multiple of 3 9 and 7? and 6? 63 6 What is the difference How many degrees is there in a full circle? between 500 cm and 1 km? 500 cm 360

Daily practice 1 to 12 times table for 10… Explain what mistakes people could make doing this and how we could avoid them

Daily practice Example: People could not partition properly and add incorrectly

Write the definitions for the words we will come across today – can you think of an example question for the word? Word Multiple Product Fraction Definition Example

$Subtracting a proper fraction from a mixed number fraction • Let’s dive straight into$

Subtracting a proper fraction from a mixed number fraction • Let’s dive straight into it!

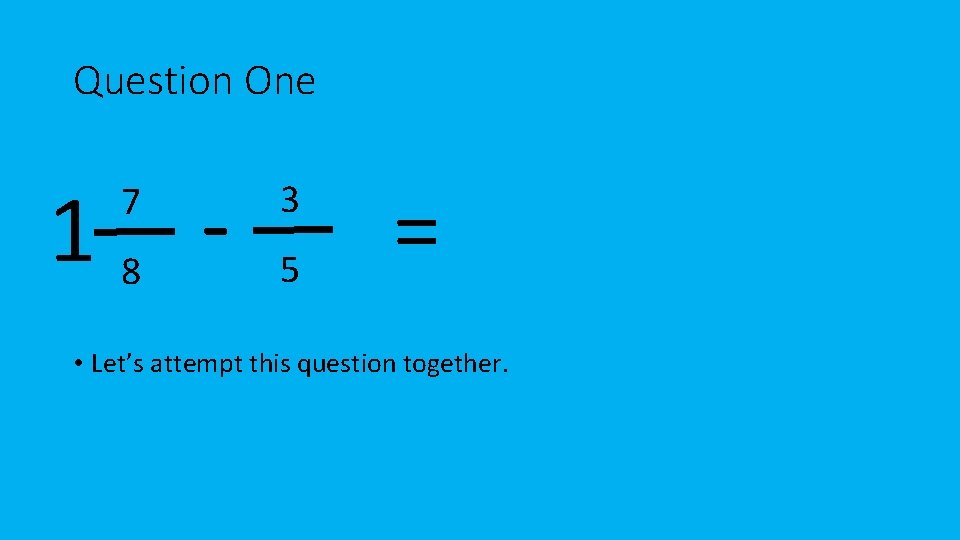
Question One 18 7 3 5 = • Let’s attempt this question together.

$Step One – convert the mixed number fraction into an improper fraction 18 =$

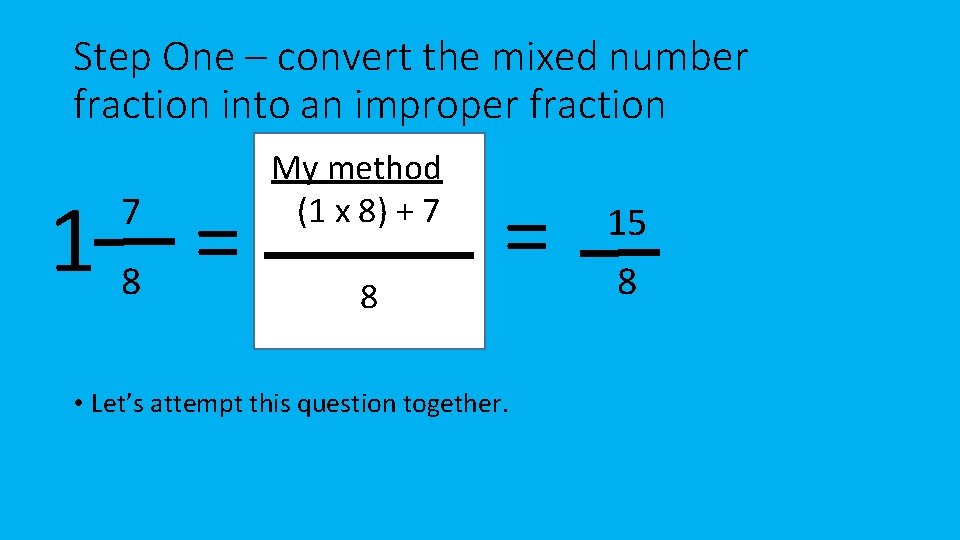
Step One – convert the mixed number fraction into an improper fraction 18 = 7 My method (1 x 8) + 7 8 = • Let’s attempt this question together. 15 8

Step Two – Make our denominator the same 15 8 - 3 5 = We have to make our denominator (bottom numbers) the same. We need to get the lowest common multiple. Let’s write out the multiples of both 8 and 5. • The multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 • The multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80 The numbers are in both 15 and 30, but let’s choose the lowest number (40).

Step Three – Set the question out like this 15 8 - 3 5 = 40 - 40 = 40 The lowest common denominator is 40. Above, I have made the original question equal to blank fractions (where there is no numerator for now). Please note that I have kept the operation the same, the subtraction sign is constant.

Step Four – Fill out the 1 st Blank Fraction numerator 1 st Fraction 15 8 - 2 nd Fraction 3 5 = 1 st Blank Fraction 75 40 - 2 nd Blank Fraction 40 = Let us make the 1 st Fraction equivalent to the 1 st Blank Fraction. I multiplied 8 by 5 to get 40. So I have to multiple 15 by 5 to get 75. 15 8 x 5 = x 5 75 40 40

Step Four – Fill out the 2 nd Blank Fraction numerator 1 st Fraction 15 8 - 2 nd Fraction 3 5 = 1 st Blank Fraction 75 40 - 2 nd Blank Fraction 24 40 = Let us make the 2 nd Fraction equivalent to the 2 nd Blank Fraction. I multiplied 5 by 8 to get 40. So I have to multiple 3 by 8 to get 24. 3 5 x 8 = x 8 24 40 40

Step Five – Subtract the numerators 1 st Fraction 15 8 - 2 nd Fraction 3 5 = 1 st Blank Fraction 75 40 - 2 nd Blank Fraction 24 40 = 51 40 I can now subtract my numerators, 75 – 24 = 51 and I can place this as the total numerator. WARNING! Our answer is an improper fraction. We need to convert this improper fraction into a mixed number fraction.

51 40 =1 40 11 • How many 40 s go into 51? 1 time right, so I have to write 1 whole. • The denominator stays the same (40). • Multiply 1 whole by 40 to get 40. How much do I add to 40 to get to 51? 11, so this is my numerator. • Can I simplify this answer/fraction? What are the factors of both 11 and 40? • 11 has factors that 1 and 11. • 40 has factors that are 1, 2, 4, 5, 8, 10, 20 and 40. • The number 1 is within both, but there is no need in dividing the numerator and the denominator by 1 because our answer will remain the same. 40 times table 40 x 1 = 40 40 x 2 = 80 40 x 3 = 120 40 x 4 = 160 40 x 5 = 200

Step Six – the finale! 18 7 3 5 = 1 40 11 I have placed my answer with the original question.

Reflection • How did you get on with working through this example? • Use your red hat to express your emotions. Write three full sentences.

Let’s go through another example. Keep persisting! You can do it!

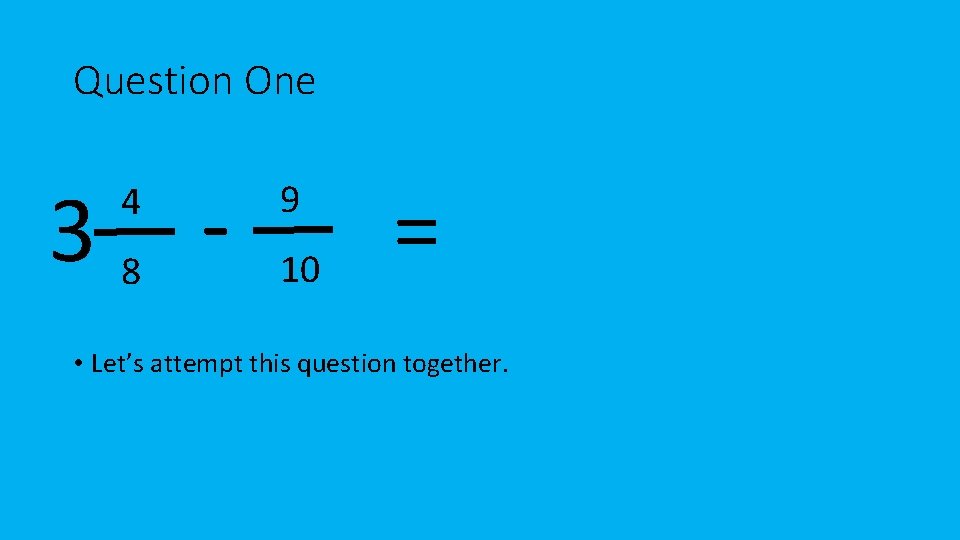
Question One 38 4 9 10 = • Let’s attempt this question together.

$Step One – convert the mixed number fraction into an improper fraction 38 =$

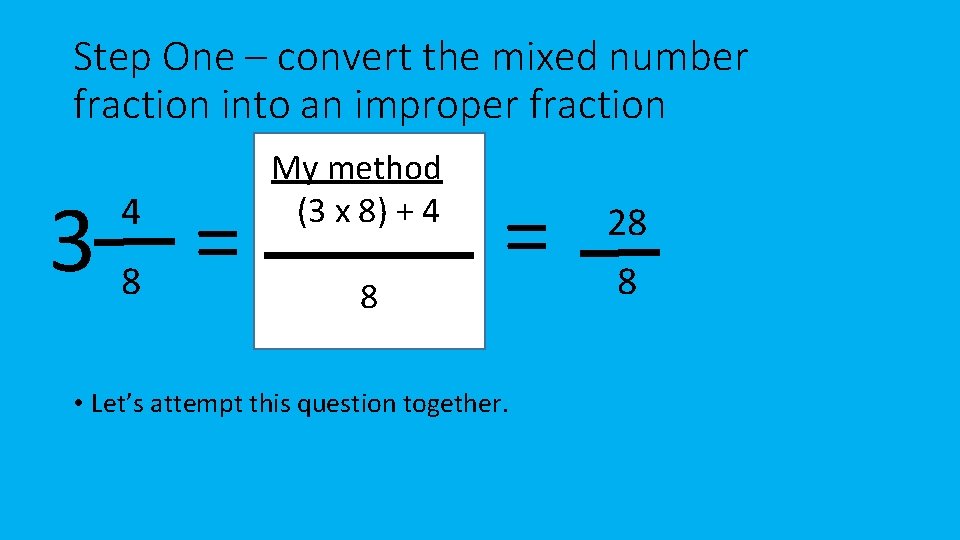
Step One – convert the mixed number fraction into an improper fraction 38 = 4 My method (3 x 8) + 4 8 = • Let’s attempt this question together. 28 8

Step Two – Make our denominator the same 28 8 - 9 10 = We have to make our denominator (bottom numbers) the same. We need to get the lowest common multiple. Let’s write out the multiples of both 8 and 10. • The multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 • The multiples of 10 are: 10, 20, 30, 40, 50, 60, 70, 80 The numbers are in both 40 and 80, but let’s choose the lowest number (40).

Step Three – Set the question out like this 28 8 - 9 10 = 40 - 40 = 40 The lowest common denominator is 40. Above, I have made the original question equal to blank fractions (where there is no numerator for now). Please note that I have kept the operation the same, the subtraction sign is constant.

Step Four – Fill out the 1 st Blank Fraction numerator 1 st Fraction 28 8 - 2 nd Fraction 9 10 = 1 st Blank Fraction 140 40 - 2 nd Blank Fraction 40 = Let us make the 1 st Fraction equivalent to the 1 st Blank Fraction. I multiplied 8 by 5 to get 40. So I have to multiple 28 by 5 to get 140. 28 8 x 5 = x 5 140 40 40

Step Five – Fill out the 2 nd Blank Fraction numerator 1 st Fraction 28 8 - 2 nd Fraction 9 10 = 1 st Blank Fraction 140 40 - 2 nd Blank Fraction 36 40 = Let us make the 2 nd Fraction equivalent to the 2 nd Blank Fraction. I multiplied 10 by 4 to get 40. So I have to multiple 9 by 4 to get 36. 9 10 x 4 = x 4 36 40 40

Step Five – Subtract the numerators 1 st Fraction 28 8 - 2 nd Fraction 9 10 = 1 st Blank Fraction 140 40 - 2 nd Blank Fraction 36 40 = 104 40 I can now subtract my numerators, 140 – 36 = 104 and I can place this as the total numerator. WARNING! Our answer is an improper fraction. We need to convert this improper fraction into a mixed number fraction.

104 40 =2 40 24 • How many 40 s go into 104? 2 time right, so I have to write 1 whole. • The denominator stays the same (40). • Multiply 2 wholes by 40 to get 80. How much do I add to 80 to get to 104? 24, so this is my numerator. • Can I simplify this answer/fraction? What are the factors of both 24 and 40? • 24 has factors that 1, 2, 3, 4, 6, 8, 12 and 24. • 40 has factors that are 1, 2, 4, 5, 8, 10, 20 and 40. • The number 8 is within both, let’s divide the proper fraction by 8. 40 times table 40 x 1 = 40 40 x 2 = 80 40 x 3 = 120 40 x 4 = 160 40 x 5 = 200

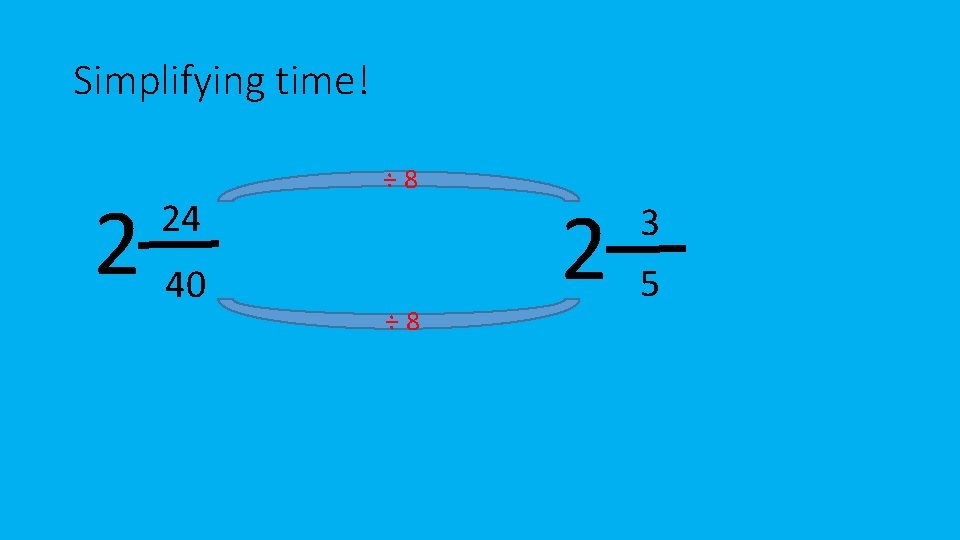
Simplifying time! 2 40 24 ÷ 8 2 3 5

Step Six – the finale! 38 4 9 10 =2 3 5 I have placed my answer with the original question.

$Make yourself a flow map to remember how to subtract proper fractions from mixed$

Make yourself a flow map to remember how to subtract proper fractions from mixed number fractions

Answer these questions

Mark your work

Try these questions

Mark your work

Exit ticket What went well today? What errors did you make or avoid today? What do you feel this lesson has made you want to learn about next?

Remember to set aside 30 minutes each day to log into TTRockstars to practice your times tables. Be sure to keep your eye out for tournaments and battles with your classmates and us, teachers. We look forward to challenging you! https: //ttrockstars. com/ If you are unsure of your username and password, please contact the office.