Subsurface Hydrology Unsaturated Zone Hydrology Groundwater Hydrology Hydrogeology

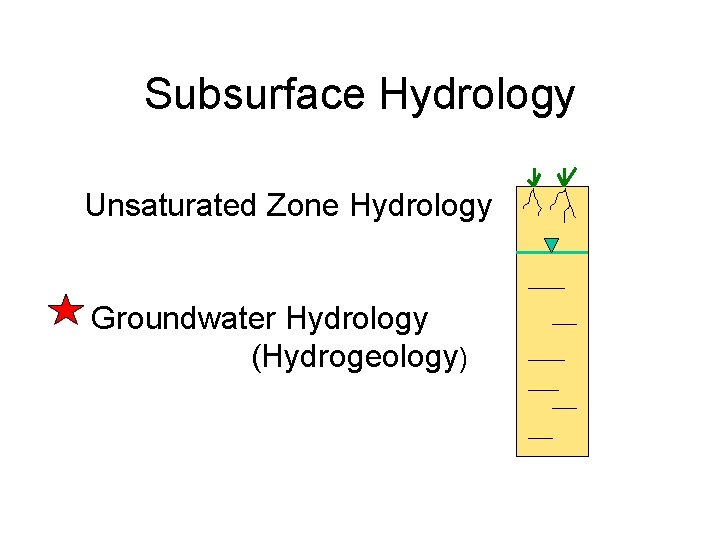
Subsurface Hydrology Unsaturated Zone Hydrology Groundwater Hydrology (Hydrogeology)

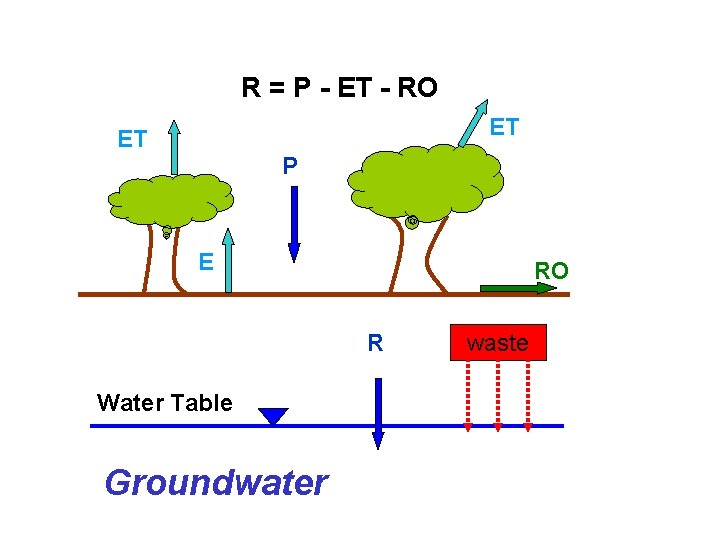
R = P - ET - RO ET ET P E RO R Water Table Groundwater waste

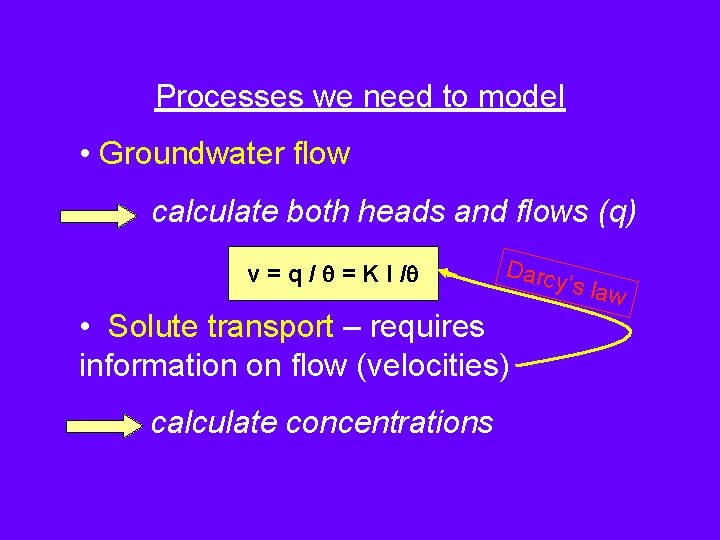
Processes we need to model • Groundwater flow calculate both heads and flows (q) v = q / = K I / Darc y’s la • Solute transport – requires information on flow (velocities) calculate concentrations w

Types of Models • Physical (e. g. , sand tank) • Analog (electric analog, Hele-Shaw) • Mathematical

Types of Solutions of Mathematical Models • Analytical Solutions: h= f(x, y, z, t) (example: Theis eqn. ) • Numerical Solutions Finite difference methods Finite element methods • Analytic Element Methods (AEM)

Finite difference models may be solved using: • a computer programs (e. g. , a FORTRAN program) • a spreadsheet (e. g. , EXCEL)

Components of a Mathematical Model • Governing Equation • Boundary Conditions • Initial conditions (for transient problems) In full solute transport problems, we have two mathematical models: one for flow and one for transport. The governing equation for solute transport problems is the advection-dispersion equation.

Flow Code: MODFLOW USGS code finite difference code to solve the groundwater flow equation • MODFLOW 88 • MODFLOW 96 • MODFLOW 2000

Transport Code: MT 3 DMS Univ. of Alabama finite difference code to solve the advection-dispersion eqn. • Links to MODFLOW

The pre- and post-processor Groundwater Vistas links and runs MODFLOW and MT 3 DMS.

Introduction to solute transport modeling and Review of the governing equation for groundwater flow

Conceptual Model A descriptive representation of a groundwater system that incorporates an interpretation of the geological, hydrological, and geochemical conditions, including information about the boundaries of the problem domain.

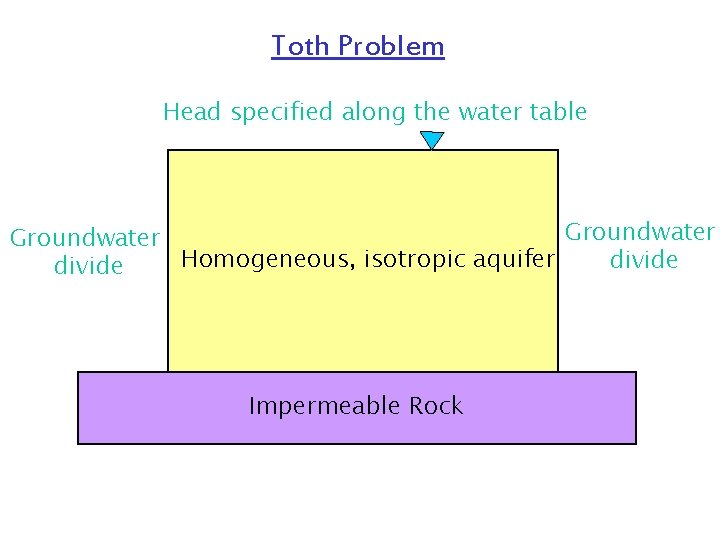
Toth Problem Head specified along the water table Groundwater Homogeneous, isotropic aquifer divide Impermeable Rock 2 D, steady state

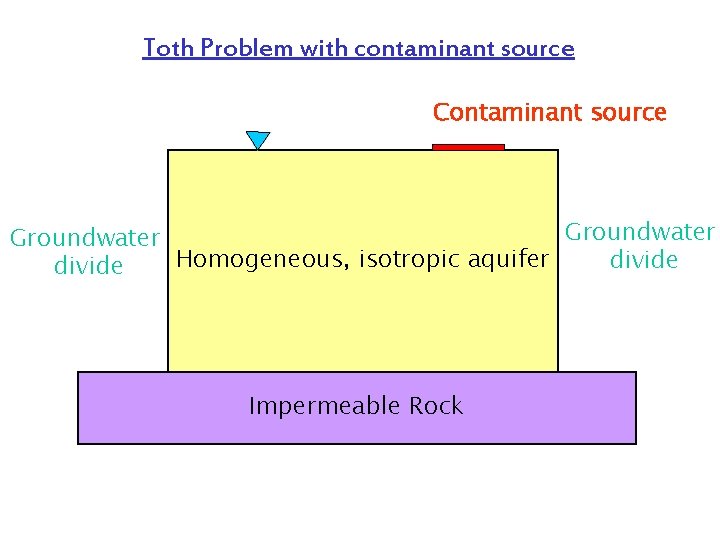
Toth Problem with contaminant source Contaminant source Groundwater Homogeneous, isotropic aquifer divide Impermeable Rock 2 D, steady state

Processes to model 1. Groundwater flow 2. Transport (a) Particle tracking: requires velocities and a particle tracking code. calculate path lines (b) Full solute transport: requires velocites and a solute transport model. calculate concentrations

Topo-Drive Finite element model of a version of the Toth Problem for regional flow in cross section. Includes a groundwater flow model with particle tracking.

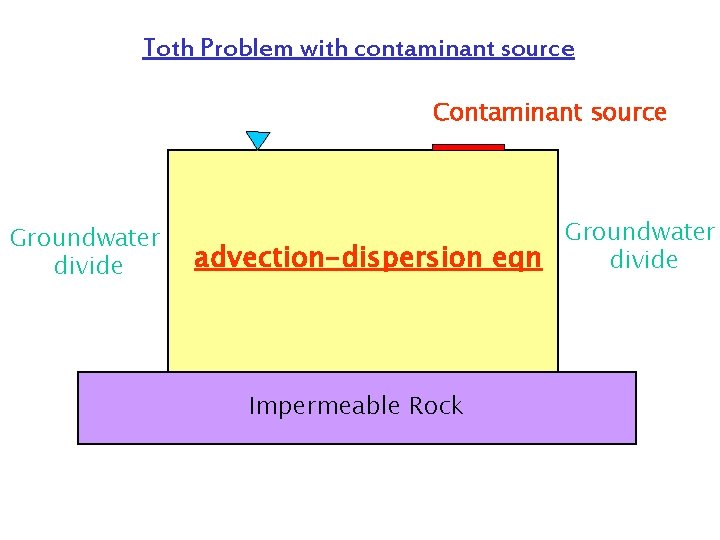
Toth Problem with contaminant source Contaminant source Groundwater divide Groundwater advection-dispersion eqn divide Impermeable Rock 2 D, steady state

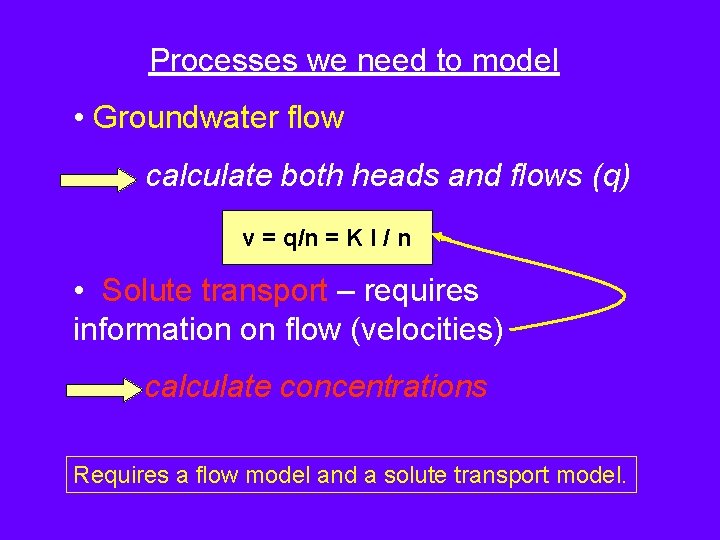
Processes we need to model • Groundwater flow calculate both heads and flows (q) v = q/n = K I / n • Solute transport – requires information on flow (velocities) calculate concentrations Requires a flow model and a solute transport model.

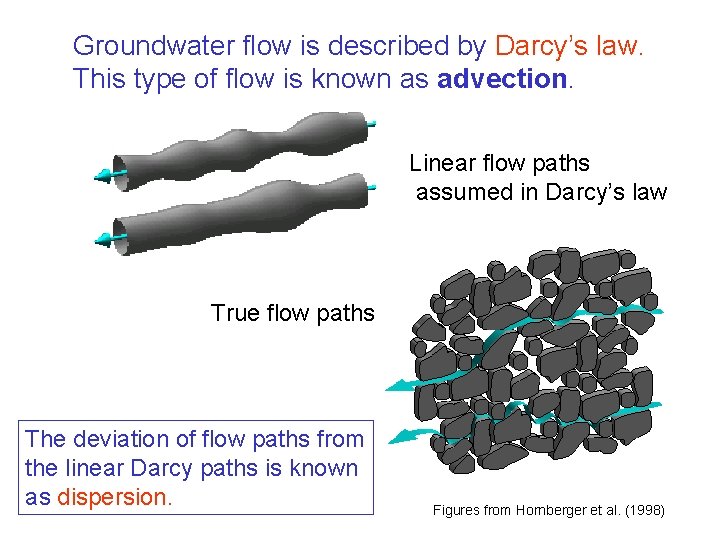
Groundwater flow is described by Darcy’s law. This type of flow is known as advection. Linear flow paths assumed in Darcy’s law True flow paths The deviation of flow paths from the linear Darcy paths is known as dispersion. Figures from Hornberger et al. (1998)

In addition to advection, we need to consider two other processes in transport problems. • Dispersion • Chemical reactions Advection-dispersion equation with chemical reaction terms.

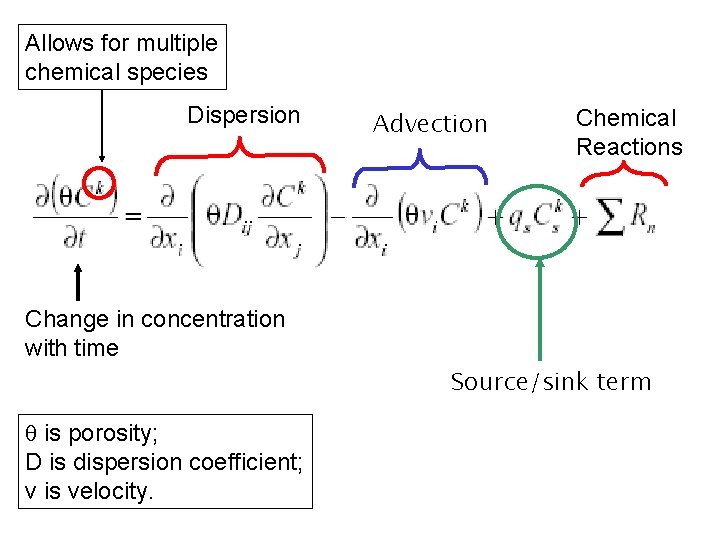
Allows for multiple chemical species Dispersion Advection Chemical Reactions Change in concentration with time Source/sink term q is porosity; D is dispersion coefficient; v is velocity.

advection-dispersion equation groundwater flow equation

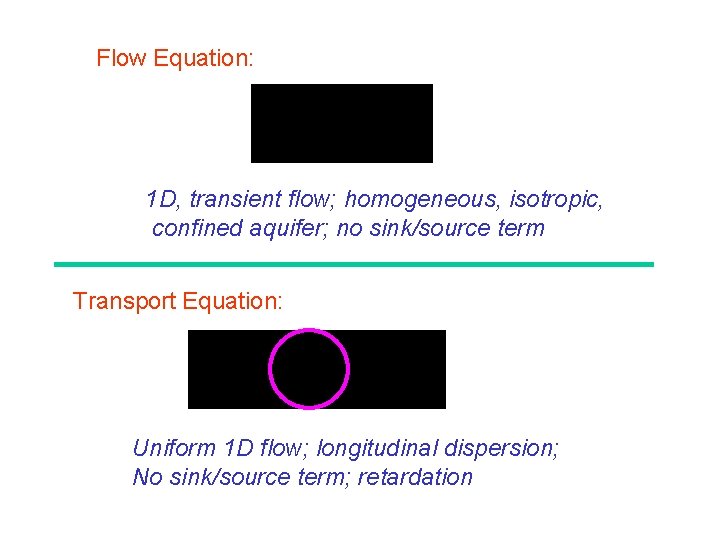
Flow Equation: 1 D, transient flow; homogeneous, isotropic, confined aquifer; no sink/source term Transport Equation: Uniform 1 D flow; longitudinal dispersion; No sink/source term; retardation

Assumption of the Equivalent Porous Medium (epm) REV Representative Elementary Volume

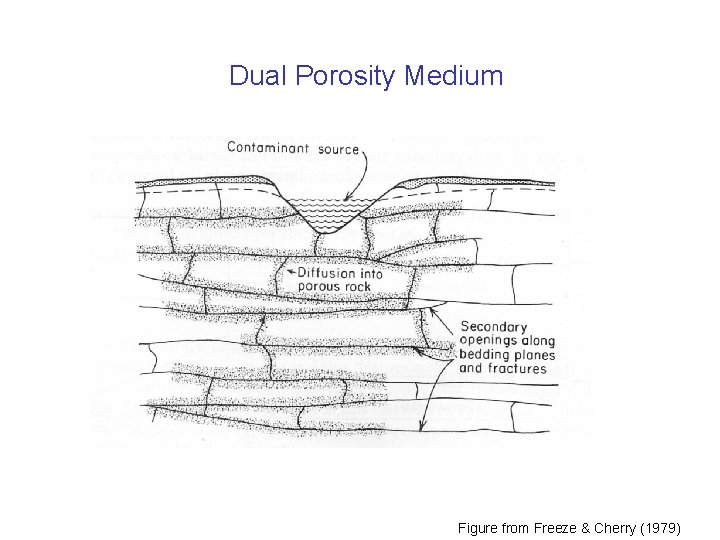
Dual Porosity Medium Figure from Freeze & Cherry (1979)

Review of the derivation of the governing equation for groundwater flow

General governing equation for groundwater flow Kx, Ky, Kz are components of the hydraulic conductivity tensor. Specific Storage Ss = V / ( x y z h)

Law of Mass Balance + Darcy’s Law = Governing Equation for Groundwater Flow -------------------------------div q = - Ss ( h t) +R* (Law of Mass Balance) q = - K grad h (Darcy’s Law) div (K grad h) = Ss ( h t) –R*

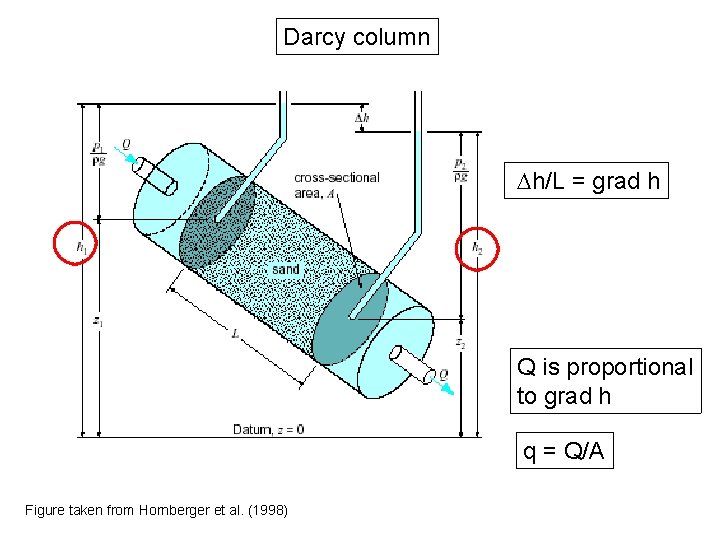
Darcy column h/L = grad h Q is proportional to grad h q = Q/A Figure taken from Hornberger et al. (1998)

q = - K grad h K is a tensor with 9 components

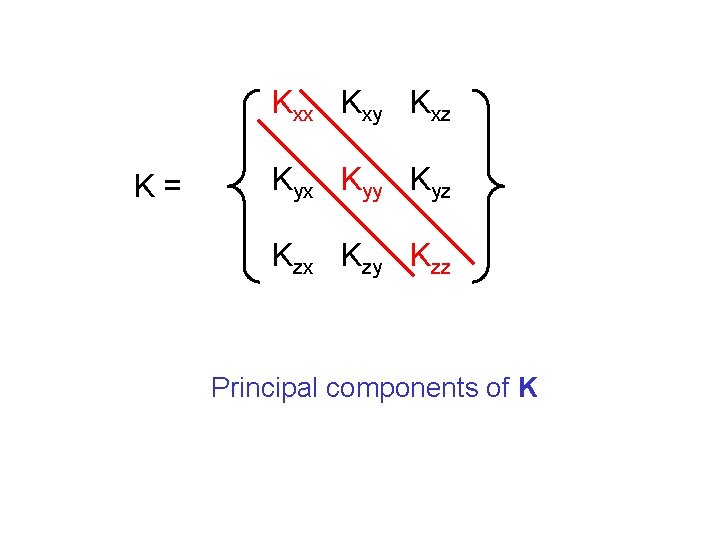
Kxx Kxy Kxz K= Kyx Kyy Kyz Kzx Kzy Kzz Principal components of K

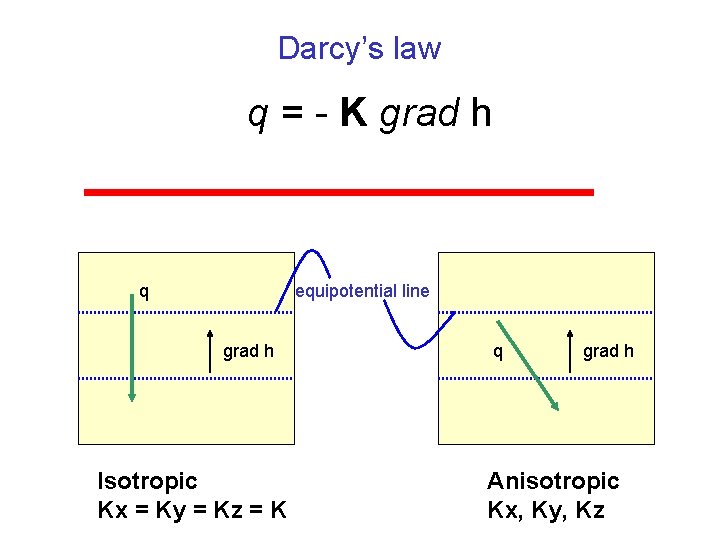
Darcy’s law q = - K grad h q equipotential line grad h Isotropic Kx = Ky = Kz = K q grad h Anisotropic Kx, Ky, Kz

q = - K grad h

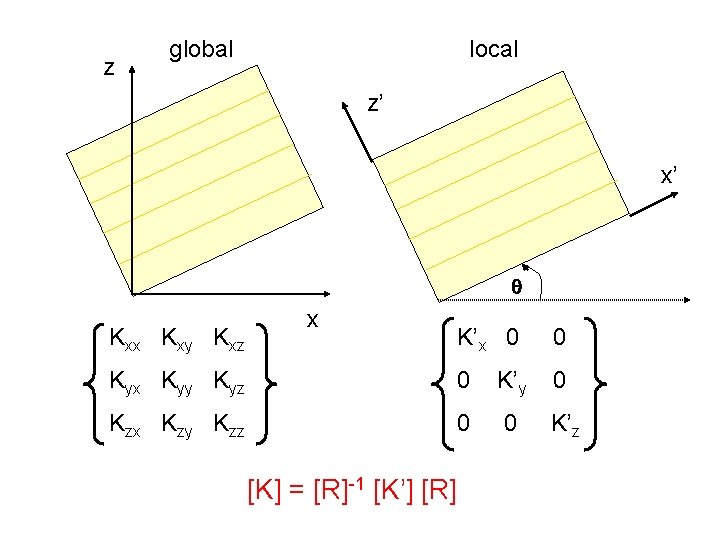
z global local z’ x’ Kxx Kxy Kxz x K’x 0 0 Kyx Kyy Kyz 0 K’y 0 Kzx Kzy Kzz 0 0 K’z [K] = [R]-1 [K’] [R]

Law of Mass Balance + Darcy’s Law = Governing Equation for Groundwater Flow -------------------------------div q = - Ss ( h t) +R* (Law of Mass Balance) q = - K grad h (Darcy’s Law) div (K grad h) = Ss ( h t) –R*

OUT – IN = x y z = change in storage = - V/ t Ss = V / ( x y z h) V = Ss h ( x y z) t t

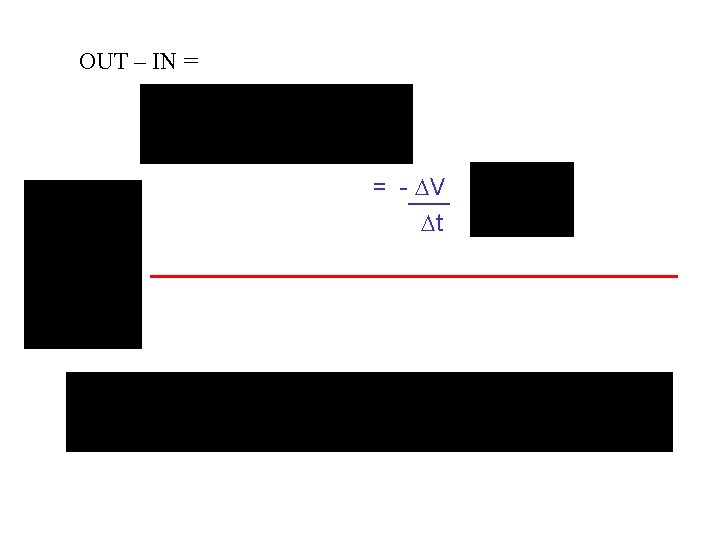
OUT – IN = = - V t

Law of Mass Balance + Darcy’s Law = Governing Equation for Groundwater Flow -------------------------------div q = - Ss ( h t) +W* (Law of Mass Balance) q = - K grad h (Darcy’s Law) div (K grad h) = Ss ( h t) –W*

2 D confined: 2 D unconfined: Storage coefficient (S) is either storativity or specific yield. S = Ss b & T = K b