Subject Name Information Theory Coding Subject Code 10

Subject Name: Information Theory Coding Subject Code: 10 EC 55 Prepared By: Shima Ramesh, Pavana Department: ECE Date: 10/11/2014 2/6/2022 MVJCE

UNIT 7 Reed –Soloman Codes 2/6/2022 MVJCE

Topics to be covered §RS codes §Golay codes §Shortened cyclic codes §Burst error correcting codes § Burst and random correcting codes

Cyclic Redundancy check (CRC) codes: CRC is well suited for error detection. Binary (n, k) CRC codes are capable of detecting following error patterns. ØAll CRC error bursts of length (n-k) or less. ØA fraction of (1 -2 ^(n-k-1)) of CRC error burst of length (n-k+1) ØAll error patterns with odd number of errors if the generator polynomial g(X) has even number of non-zero coefficients. ØA fraction (1 -2^(n-k)) of CRC error burst of length greater than (nk+1)

Generator Polynomial of Three CRC codes:

Maximum Length codes: for any integer m>=3, the maximum length codes exist with parameters. Maximum length codes are generated by polynomials Of the form Maximum length codes are generated by polynomials of degree m

Cyclic codes generated by a primitive polynomial is a hamming code of dmin=3 v. Maximum length codes are duals of hamming codes. Majority logic Decodable codes. ØThese codes form a smaller sub-class of cyclic codes. ØDecoding of these codes can be done by using simple circuits.

Shortened Cyclic codes. Why shortened cyclic codes are required: the generator polynomials for cyclic codes are determined among the divisor of X^n+1. ØSince there are fewer divisors for a given n, k there are very few cyclic codes of given length. To over come this difficulty cyclic codes are used in there shortened form. Shortened cyclic codes: The last j information digits are always taken to be zero and are not transmitted. In decoding, the decoder for the original cyclic codes can decode the shortened cyclic codes by padding the received (n-j) tuples with j zeros. Hence (n-j, k-j ) shortened cyclic codes can be constructed from (n, k) cyclic codes.

Golay codes: ØGolay code is (23, 12) perfect binary code that is capable of correcting any combination of three or fewer random errors in block of 23 bits. ØIt’s a prefect code because it satisfies the hamming bound with the equality sign for t=3 as The generator polynomial for the code is obtained from the relation

Where The code has minimum distance, dmin=7 The extended golay code (924, 12) code has dmin=8 The perfect ternary (11, 6) golay code with dmin=5

Reed-Solomon codes(RS): Reed solomon are important subclass of BCH codes. A t-error correcting RS codes has following parameters. The encoder for an RS(n, k) code on m-bits symbols groups the incoming Binary data streams into blocks, each km bits long. Each block is treated as k symbols with each symbol having m bits. The encoding algorithm expands a block of k symbols By adding (n-k) redundant symbols.

Every RS code is maximum-distance separable code. {any linear block code fro which dmin=(n-k-1) is called maximum distance separable code}. Advantages of RS code. (a) (b) (c) They make highly efficient use of redundancy and can be adjusted to accommodate wide range of message sizes. They provide with wide range of code rates(k/n) that can be chosen to optimize performances. Efficient decoding techniques are available.

Burst and Random error correcting codes. ØConsider a channels which has random and burst errors. Its better to design a codes that can correct both types of errors. One technique introduced is time-diversity or interleaving. ØInterleaving the code vectors before transmission and de-interleaving after reception causes the burst error to spread out in time and decoder can handle them as if they are random errors.

Illustrating interleaving Consider fig a: it is assumed to have single error correcting capability within each six-symbol sequence. If the memory span of channel is one code word Duration, a six symbol time noise burst could destroy the information contained One or two code words.

Consider fig b: code symbol of each code word is separated from its preinterleaved neighbors by span of six symbol times. Upon reception, the stream is de-interleaved and decoded as though a single-random error has occurred in each code word. v. The burst noise has no degrading effect on the final sequence.

Block Interleaving. ØGiven an (n, k) cyclic codes, it is possible to construct a Cyclic interlaced code by simple arranging Code vectors of the into Rows of rectangular array and then transmitting them Column by column Parameter lambda is called degree of interlacing. ØIf the original code can correct single errors then the interlaced code can correct single burst of length lamda or less. ØIf the original code has an error correcting capability of t, t>1 then the interlaced code is capable of correcting any combination of t-error bursts of length lambda or less.

Block interleaver accepts the coded symbols in blocks from the encoder, permutes the symbol and the feeds the re-arranged symbols to the modulator. Ø The permutation of block can be achieved by ‘filling the rows ’ of a ‘lamda’ row by ‘n’-column array with the encoded sequence. ØThe de-inter leaver accepts the symbols from de-modulator de-inter leaves them and feeds them to decoder. Symbols are entered into de-inter leaver array by columns and removed rows.

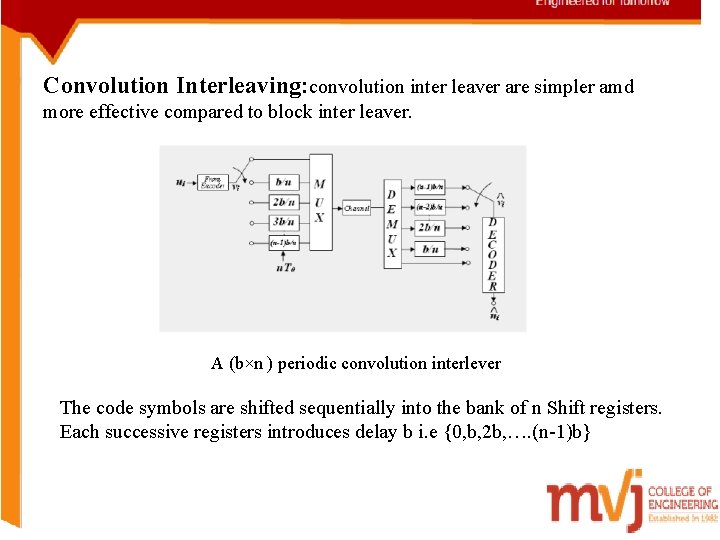
Convolution Interleaving: convolution inter leaver are simpler amd more effective compared to block inter leaver. A (b×n ) periodic convolution interlever The code symbols are shifted sequentially into the bank of n Shift registers. Each successive registers introduces delay b i. e {0, b, 2 b, …. (n-1)b}

ØBecause of this, the symbols of one code word are placed at a distance of b-symbol units in the channel stream and the burst of length b separated by guard space of (n-1)b symbols units only affect one symbol per code word. ØIn the receiver , code words are re-assembled through complementary delay units and decoded to correct single errors so generated.