Subject Name Information Theory Coding Subject Code 10

Subject Name: Information Theory Coding Subject Code: 10 EC 55 Prepared By: Shima Ramesh, Pavana Department: ECE Date: 10/11/2014 12/14/2021 MVJCE

Unit 6 Binary cyclic codes 12/14/2021 MVJCE

Topics to be covered §Binary cycle codes, §Algebraic structure of cyclic codes §Encoding using (n-k) bit shift register, syndrome calculation §BCH codes.

Bose-chaudhury-Hocquenghem(BCH) codes: ØBCH codes are one of the most important and powerful errorcorrecting cyclic codes known. ØThe most common BCH codes are characterized as follows, specifically, for any positive integer m>=3 and t<2^m-1/2 there exist a binary BCH code with the following parameters

BCH codes are ‘t-error correcting codes’: ØThe BCH codes are best known codes among those which have block lengths of few hundred or less. ØThe major advantage of these codes lies in the flexibility in the choice of code parameters i. e block length and code rate.

Syndrome calculation: ØSuppose the code vector v=(v 0, v 1, v 2…. vn-1) is transmitted over a noisy channel. The received code vector r=(r 0, r 1, r 2…. rn -1), ØThe function of decoder is to determine the transmitted code vector based on the received vector. ØThe decoder first computes the syndrome to check whether or not the received code vector is valid code vector.

ØIn cyclic codes, if the syndrome is zero, then the received code word polynomial must be divisible by the generator polynomial. ØIf the syndrome is non-zero, the received word contains transmission errors and needs error correction. Consider the received code vector R(X) and is given by Let A(X) be the quotient and S(X) be the remainder polynomials Resulting from the division of R(X) by g(X)

S(X) is the syndrome polynomial of degree (n-k-1) or less. If E(X) is the error pattern caused by the channel then R(X)=V(X)+E(X) where V(X)=U(X). g(X) E(X)=[A(X)+U(X)]g(X) +S(X) The syndrome of R(X) is equal to the remainder resulting from dividing the error pattern by generator polynomial. Syndrome contains information about the error pattern, which can be used fro error correction.

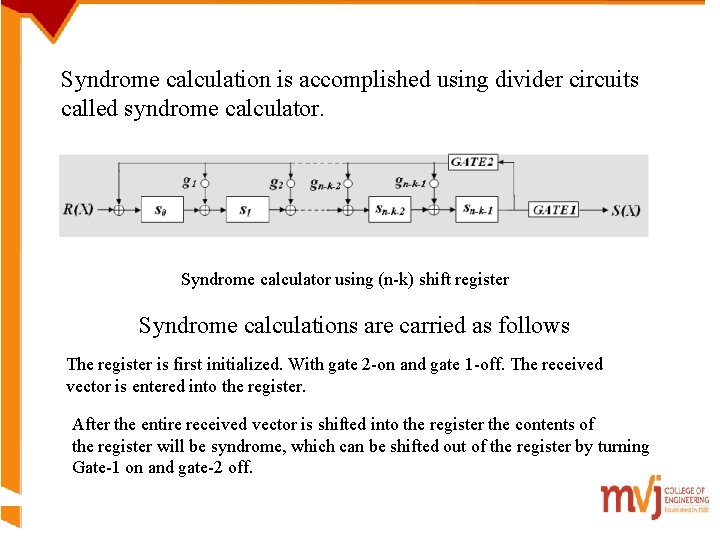
Syndrome calculation is accomplished using divider circuits called syndrome calculator. Syndrome calculator using (n-k) shift register Syndrome calculations are carried as follows The register is first initialized. With gate 2 -on and gate 1 -off. The received vector is entered into the register. After the entire received vector is shifted into the register the contents of the register will be syndrome, which can be shifted out of the register by turning Gate-1 on and gate-2 off.

Error detection can be achieved by adding additional RS flip flop to the syndrome calculator. Error correction procedure: Step 1: Received data is shifted into the buffer register and syndrome register with switches Sin closed and Sout open. Error correction is done with Sin open and Sout closed. Step 2: After the syndrome for the received code is calculated and placed in syndrome register, the contents are read into error detector. (i) If the detector output is 1 then the received digit at the right most stage of the buffer register is assumed to be in error and is corrected. (ii) If the detector output is 0 then the received digit at the right most stage of the buffer is assumed to be correct.

Step 3: the first received digit in the syndrome register is shifted right once. If the received digit has error the output of detector will be 1. The output of the detector is also fed to the syndrome register to modify the syndrome. this result in new syndrome is corresponding the altered received code word is shifted to right by one place. Step 4: the new syndrome is used to check and correct the second received digit, which is now at the right most position, is an erroneous digit. If so it is corrected a new syndrome is calculated at step 3 and the procedure is repeated.

Step 5: The decoder operates on the received data digit by digit until the entire received code word is shifted out of the buffer. At the end of the decoding operation after the received code is shifted out of the buffer all those errors will have been corrected and the syndrome register will contain all zeros. If the syndrome registers dose not contain zeros this means an uncorrectable error pattern has been detected.

Binary codes. Let source be characterized by set of symbols. S={s 1, s 2…. sq} let S be the source alphabet. Consider another set X consisting of r symbols. X={x 1, x 2…. xr} where X represents code alphabet. ØCoding means representing each and every symbol of S by a sequence of symbols of X such that there shall be one-to-one relationship. ØAny finite sequence of symbols from the alphabet X forms a code word. The total number of symbols contained in the word will be called word length

Basic properties: (1) Block codes: A block code is one in which a particular message of the source is always encoded into the same fixed sequence of the code symbol. example: source alphabet S={s 1, s 2, s 3, s 4} code alphabet X={0, 1} the code words C={0, 11, 10, 11} (2) Non-singular codes: A block code is said to be non-singular if all the words of the code set X 1 are “distinct”. If the codes are not distinguishable on a simple inspection we say the code set is singular in the small. example: Source alphabet S={s 1, s 2, s 3, s 4} X={0, 1} codes C={0, 11, 10, 01} (3) Uniquely decodable codes: A non-singular code is uniquely decipherable, if every word immersed in a sequence of words can be uniquely identified. “the nth extension of the code be non-singular for every finite n”

(4) Instantaneous codes: A uniquely decodable code is said to be “instantaneous ” if the end of any code word is recognized with out the need of inspection of succeeding code symbols. Prefix property: “A necessary and sufficient condition for a code to be instantaneous is that no complete code word be a prefix of some other code word. ” (5) Optimal codes: An instantaneous code is said to be optimal if it has “minimum average word length” for a source with a given probability assignment for the source symbols.

Ø consider source symbols si with prob Pi and has code word length li consider Source sj with prob Pj and has a code word length lj. ØIf Pi > Pj and li < lj then the average length L 1 is given by L 1=Pi. li+ Pj. lj Now suppose we interchange code words so that lj corresponds to si and li corresponds to sj, then the average length becomes L 2= Pi. lj+Pj. li then L 2 -L 1=Pi(lj-li)+Pj(li-lj) = (Pi-Pj)(lj-li) Since by assumption Pi>Pj and li<lj (L 2 -L 1) is positive. If the code satisfies all the five properties it is called irreducible code.

Quick reference of the basic requirements of the codes

Requirements in the terms of tree diagram

Construction of instantaneous codes: consider encoding of a 5 symbol source into binary instantaneous codes: S={s 1, s 2, s 3, s 4, s 5}; X={0, 1} The possible instantaneous code is given is s 1 - 00 s 2 - 01 s 3 - 10 s 4 - 110 s 5 - 111 One observation is shorter we make the first few words, the longer we will have to make the later code words.

Kraft inequality: given a source S={s 1, s 2…. sq} let the word length of the codes be l 1, l 2, l 3…lq and code alphabet be X={x 1, x 2, …. xr} then the instantaneous code for the source exists Mc. Millan’s Inequality: both Mc. Millan’s inequality and kraft inequality Are one and the same, only difference is in the approach to derive inequality. The two implications of Kraft-Mcmillan (K-M) inequality are (i) Given a set of word lengths it is possible to construct a instantaneous if and only if the word lengths satisfy the K-M inequality. (ii) Already existing code is uniquely decodable if and only if satisfies the K-M inequality

Code efficiency and redundancy: Code efficiency: code efficiency is the ratio of the average information per symbol of the encoded language to the maximum possible information per code symbol. Redundancy of the code:

Cyclic codes: Binary cyclic code form a sub class of linear block codes. A binary code is said to be cyclic if it satisfies two condition: (i)Linearity property: A sum of code word is also a code word (ii)cyclic property: Any lateral shift of code word is also a code word Illustration of cyclic property:

If n-tuple read from A in the CW Is code vector Then the code vector read from B in CW direction obtained by one bit cyclic Right shift is a code vector given by In this way, n-tuple obtained successive cyclic right shifts are all code vectors This property of cyclic codes enables us to treat the elements of each code vector As the co-efficients of polynomial of degree (n-1)

Code polynomial V(X) can be written us Each power of X in V(X) represents a one bit cycle shift in time. Therefore multiplication of V(X) by X may be viewed as a cyclic shift or rotation To the right subject to the condition (X^n=1). This condition (i) restores XV(X) to the degree (n-1) (ii) implies that the right most bit is fed back at the left. This special form of multiplication is called multiplication modulo X^n+1

Generator polynomial for cyclic codes: An (n, k) cyclic code is specified by the complete set of code polynomial of degree <=(n-1) and contains a polynomial of g(X), of degree (n-k) factor called the generator polynomial of the code. This polynomial has minimum degree and is unique. Theorem : “If g(X) is a polynomial of degree (n-k) and is a factor of (X^n+1) then g(X) generates an (n, k) cyclic code in which the code polynomial V(X) for data vector u= (uo, u 1…. . uk-1) is generated by V(X)= U(X)g(X) Where U(X) is the data polynomial of degree (k-1)

Multiplication Circuits consider polynomial Where ai is either 0 or 1 The product of two polynomial A(X) and B(X) yields The above equation can be realized using a multiplication circuits

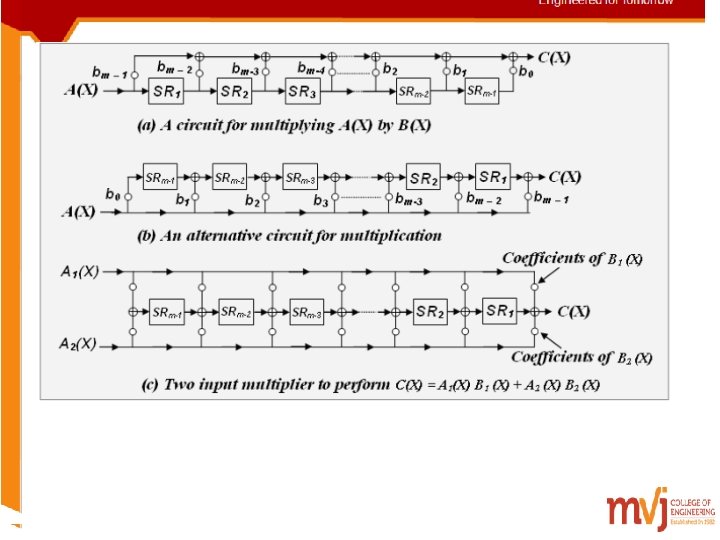
Consider that a polynomial A(X) is to multiplied by

Dividing Circuits: Division of A(X) and B(X) can be accomplished by using shift registers and mod-2 adders In division circuit the first coefficient of the quotient is And q. B(X) is subtracted from A(X). The process will continue for 2 nd and Subsequent terms. After (n-1) shifts the entire quotient will appear at the output And the remainder is stored in shift registers.

Systematic cyclic codes. : Scheme to generate systematic cyclic codes: The generator polynomial is written as 1. The switch S is in position 1 to allow transmission of the message bits directly to an output shift register during the first k-shifts.

ØAt the same time the gate is on to allow transmission of the message bits into the (n-k) stage encoding shift register. ØAfter transmission of the kth message bit the gate is turned off and the switch S is moved to position 2. Ø(n-k) zeros introduced at “A” after step 3, clear the encoding register by moving the parity bits to the output register. ØThe total number of shifts is equal to n and the contents of the output register is the code word polynomial V(X)=P(X)+X^(n-k) U(X) After step 4 the encoder is ready to take up encoding of the next message input.