Subdivision Surfaces Dr Scott Schaefer 1 Bspline Surfaces

Subdivision Surfaces Dr. Scott Schaefer 1
B-spline Surfaces 2/130

B-spline Surfaces 3/130
B-spline Surfaces 4/130

B-spline Surfaces 5/130

B-spline Surfaces 6/130

B-spline Surfaces 7/130
B-spline Surfaces 8/130

B-spline Surfaces 9/130

B-spline Surfaces 10/130

B-spline Surfaces 11/130

B-spline Surfaces 12/130

B-spline Surfaces 13/130
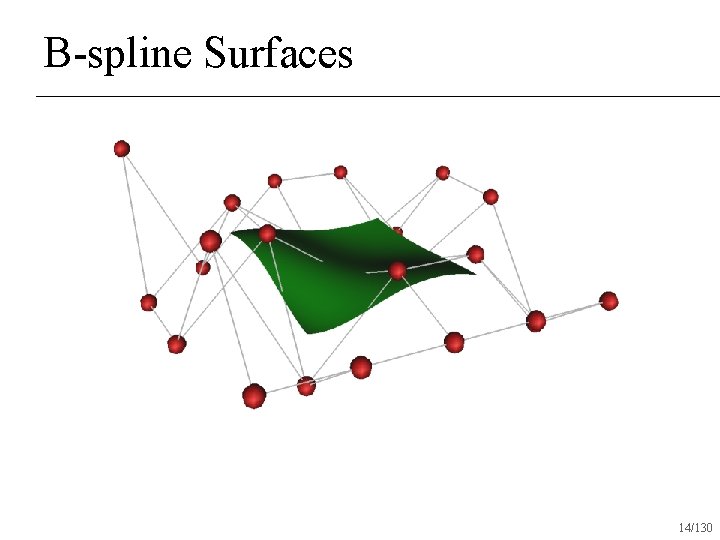
B-spline Surfaces 14/130
B-spline Surfaces Example 15/130
B-spline Surfaces Example 16/130
B-spline Surfaces Example 17/130
B-spline Surfaces Example 18/130
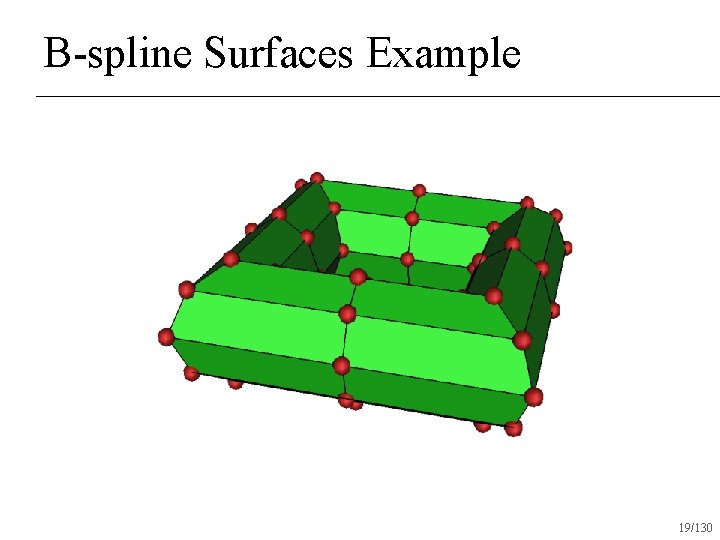
B-spline Surfaces Example 19/130
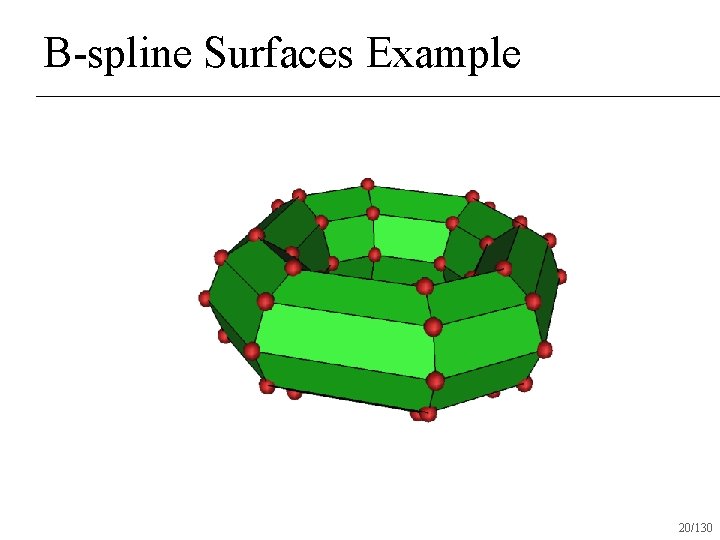
B-spline Surfaces Example 20/130
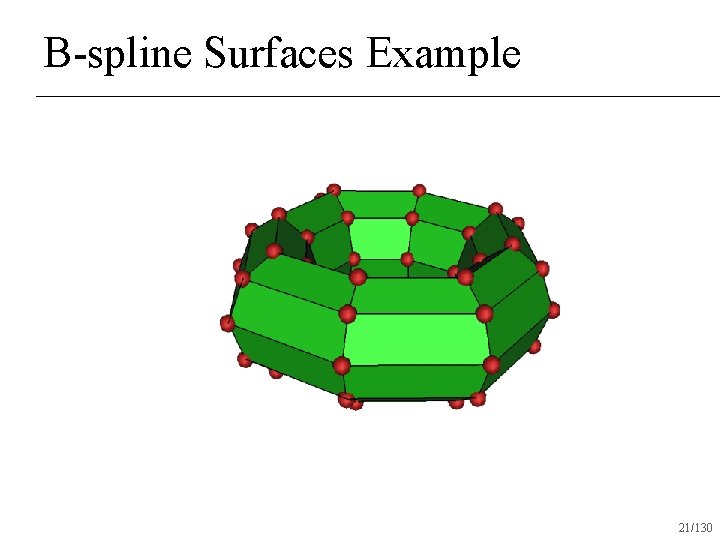
B-spline Surfaces Example 21/130

B-spline Surfaces Example 22/130

B-spline Surfaces Example 23/130
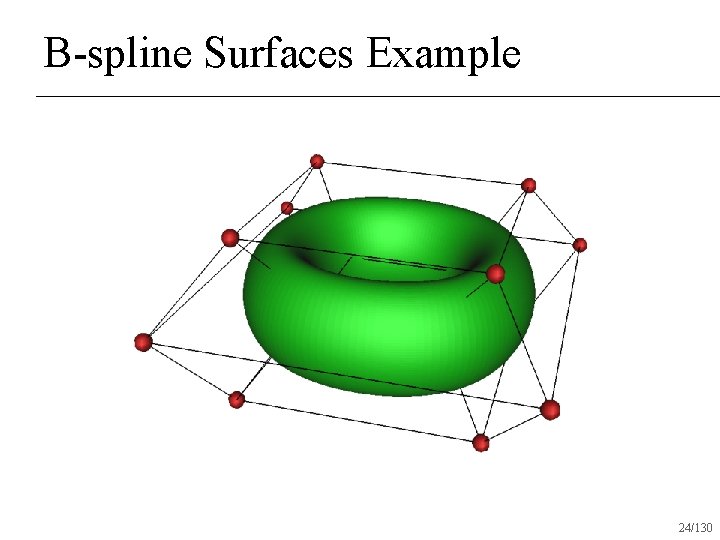
B-spline Surfaces Example 24/130

B-spline Surface – Properties Surface inside convex hull of control points n Guaranteed to be smooth everywhere n Smoothness is determined by number of averaging steps n 25/130
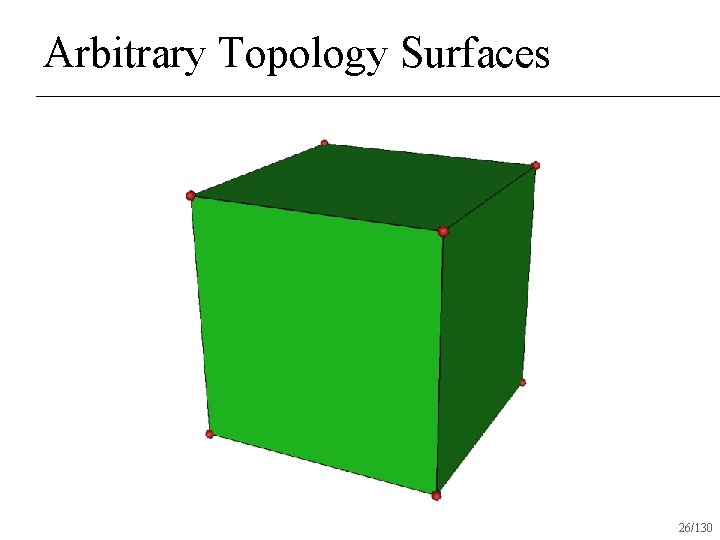
Arbitrary Topology Surfaces 26/130
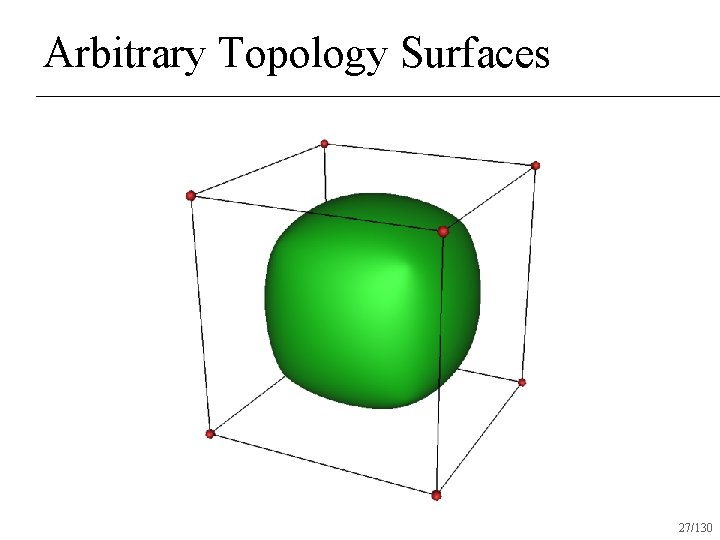
Arbitrary Topology Surfaces 27/130

Subdivision Surfaces Used in movie and game industries n Supported by most 3 D modeling software n Toy Story © Disney / Pixar Geri’s Game © Pixar Animation Studios 28/130

Subdivision Surfaces Set of rules S that recursively act on a shape n Arbitrary topology surfaces n Smooth everywhere n 29/130

Repeated Averaging Assume surface is made out of quads u Any number of quads may touch a single vertex n Subdivision rules: linear subdivision followed by averaging n 30/130
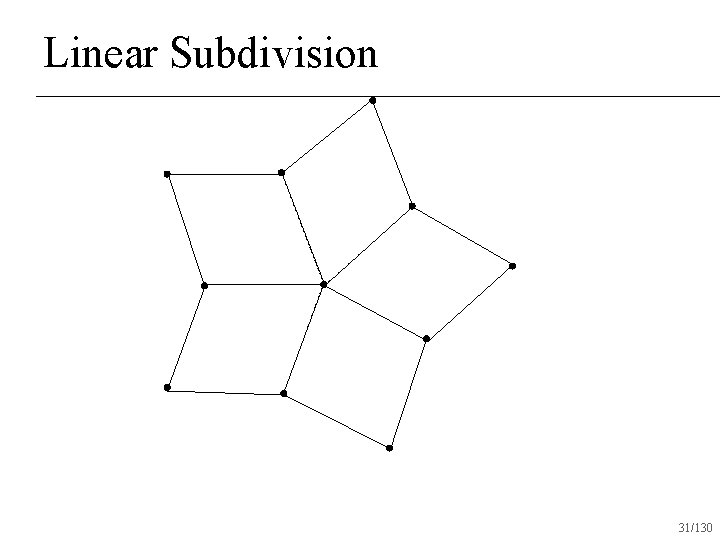
Linear Subdivision 31/130
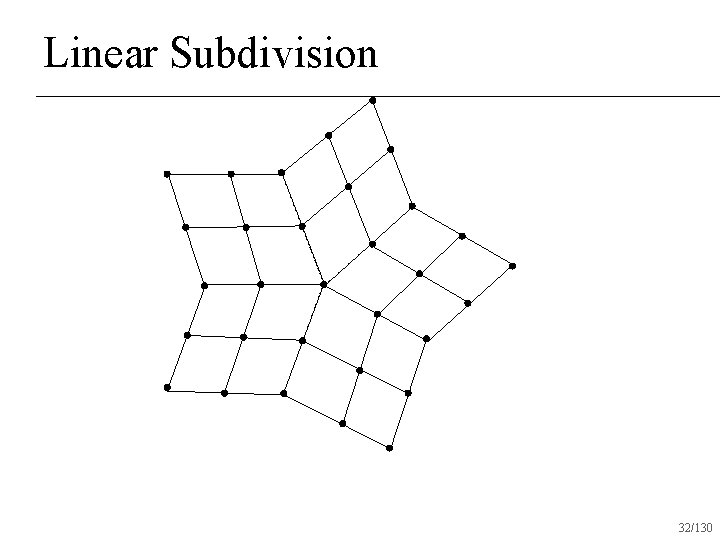
Linear Subdivision 32/130
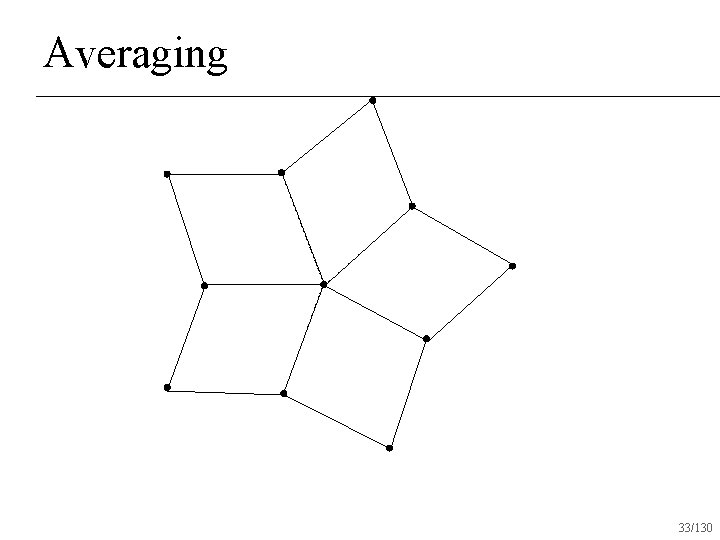
Averaging 33/130
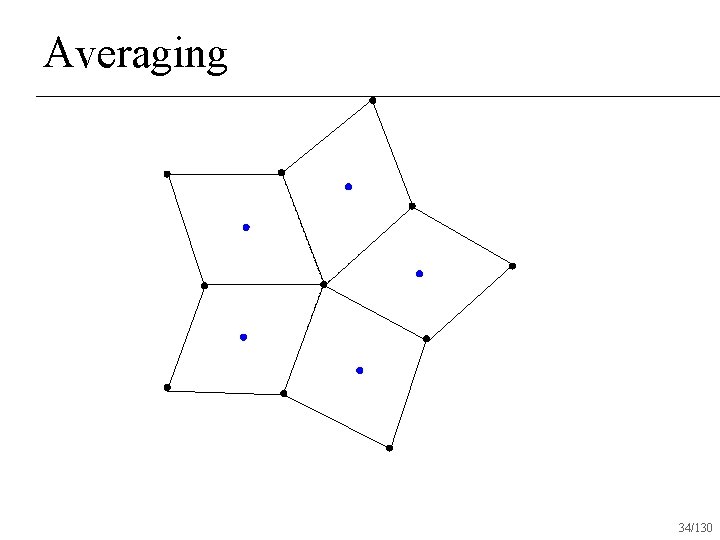
Averaging 34/130
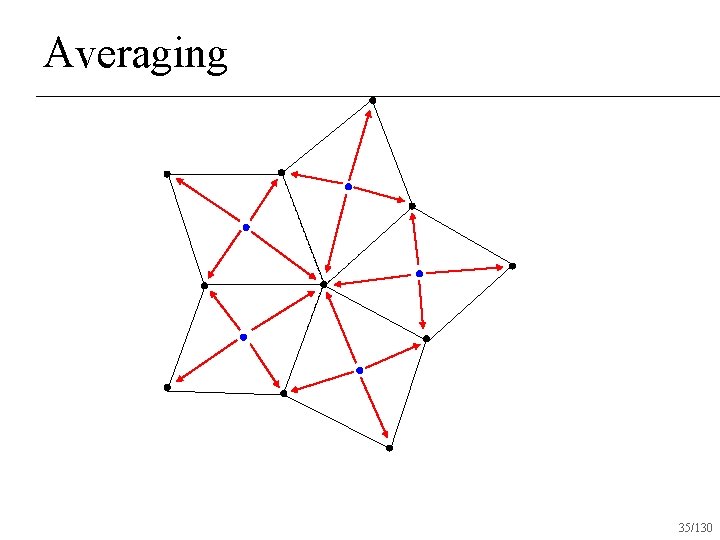
Averaging 35/130
Subdivision Surfaces – Examples 36/130
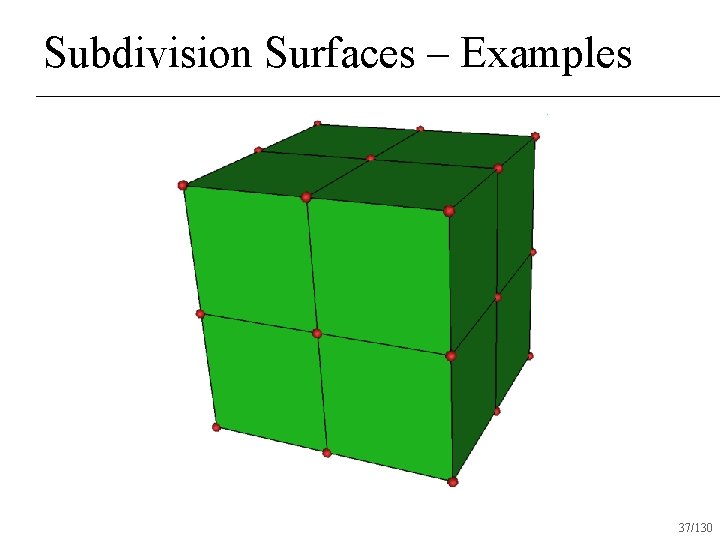
Subdivision Surfaces – Examples 37/130

Subdivision Surfaces – Examples 38/130

Subdivision Surfaces – Examples 39/130

Subdivision Surfaces – Examples 40/130

Subdivision Surfaces – Examples 41/130

Subdivision Surfaces – Examples 42/130

Subdivision Surfaces – Examples 43/130
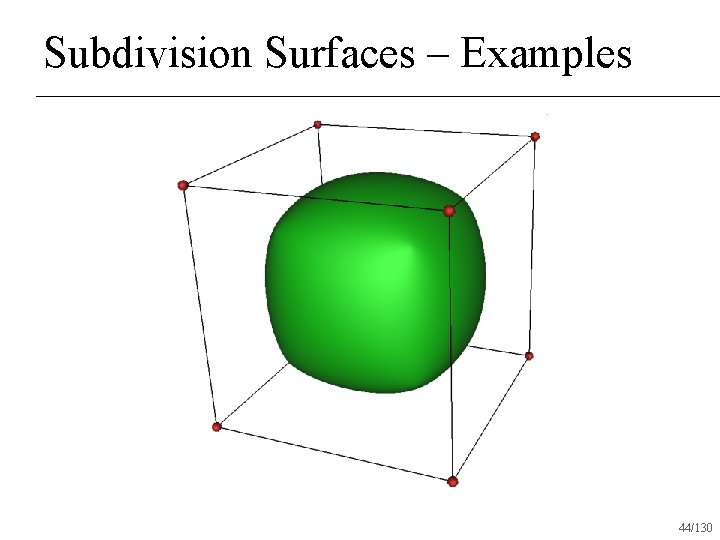
Subdivision Surfaces – Examples 44/130

Implementing Linear Subdivision linear. Sub ( F, V ) new. V = V new. F = {} for each face Fi for j = 1 to 4 ej = get. Vert ( Fi, j, Fi, j+1) add centroid to new. V and store index in c for j = 1 to 4 add face (Fi, j, ej, c, ej-1) to new. F return (new. F, new. V) 45/130

Implementing Linear Subdivision get. Vert ( i 1, i 2 ) if orderless key (i 1, i 2) not in hash add midpoint of V[i 1], V[i 2] to new. V hash[(i 1, i 2)] = index of new point return hash[(i 1, i 2)] 46/130

Implementing Average( F, V ) new. V = 0 * V val = array of 0 whose size is number of vertices new. F = F for each face Fi cent = centroid for Fi new. V[Fi] += cent val[Fi] += 1 for each vertex new. V[i] /= val[i] return (new. F, new. V) 47/130

Subdivision Surfaces – Examples 48/130
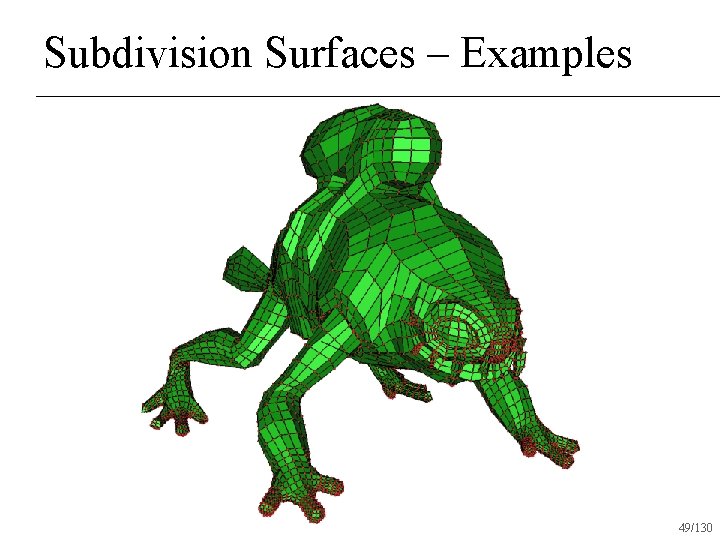
Subdivision Surfaces – Examples 49/130
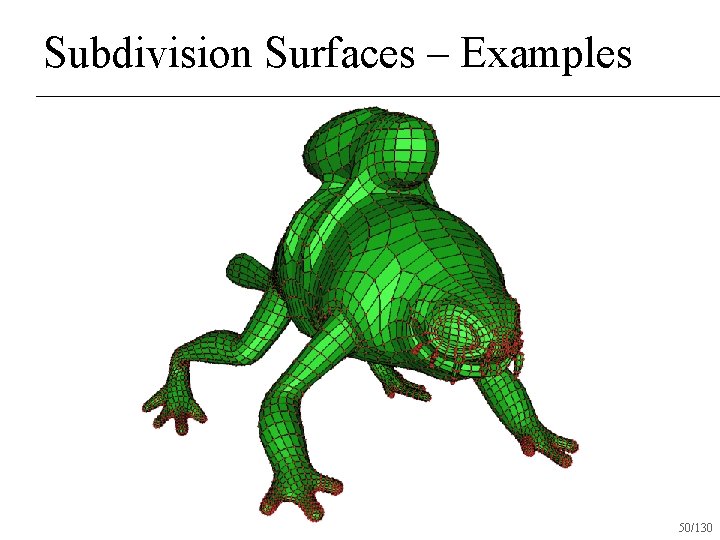
Subdivision Surfaces – Examples 50/130
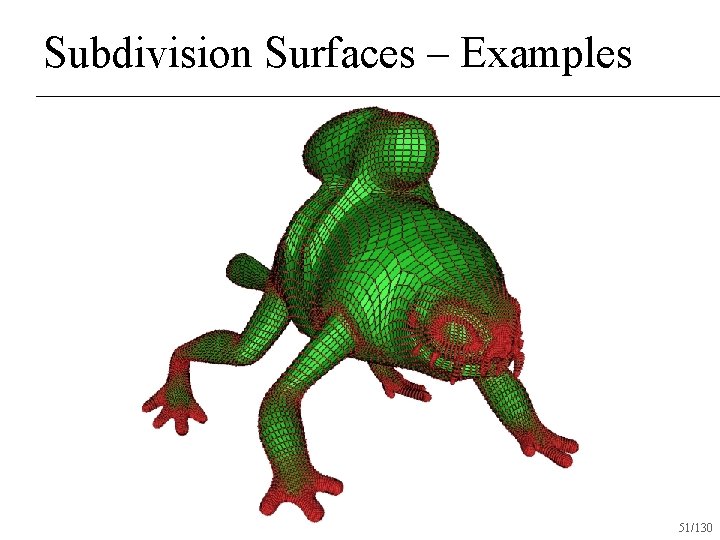
Subdivision Surfaces – Examples 51/130
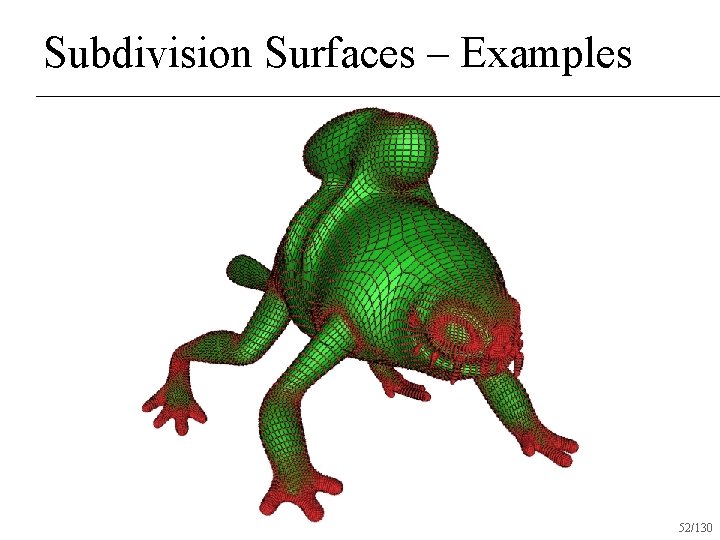
Subdivision Surfaces – Examples 52/130

Subdivision Surfaces – Examples 53/130
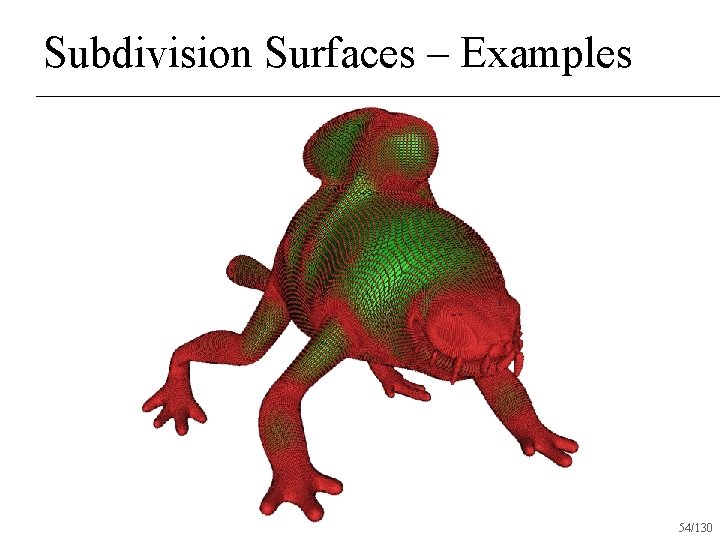
Subdivision Surfaces – Examples 54/130
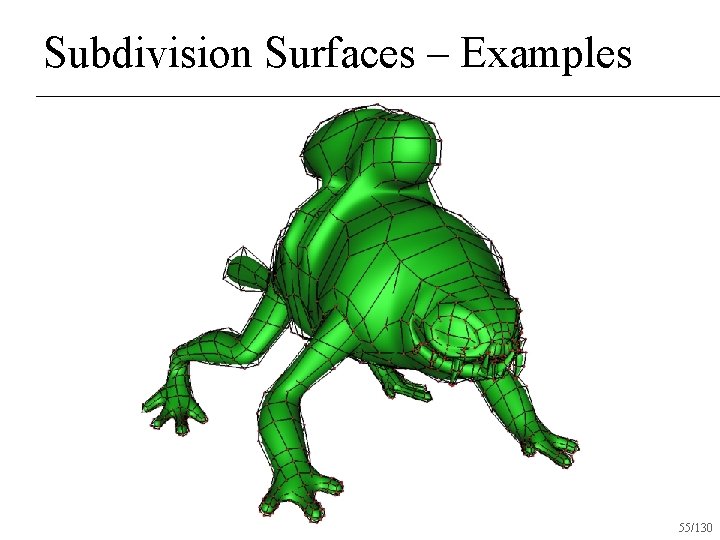
Subdivision Surfaces – Examples 55/130
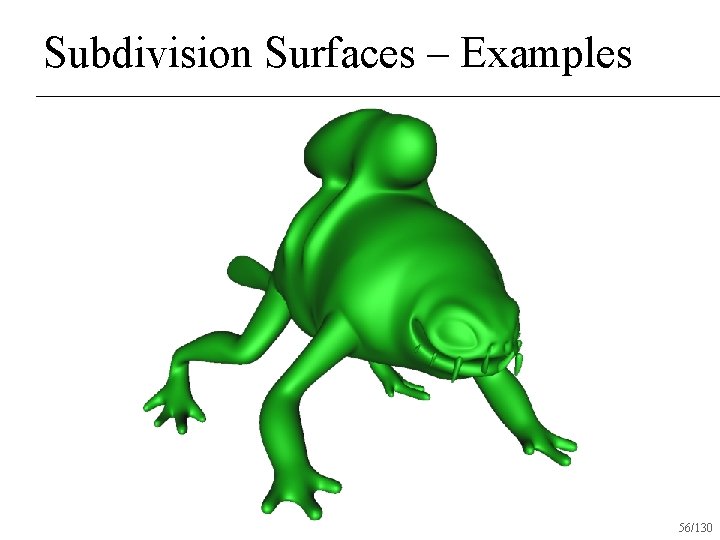
Subdivision Surfaces – Examples 56/130

Subdivision Surfaces – Examples 57/130
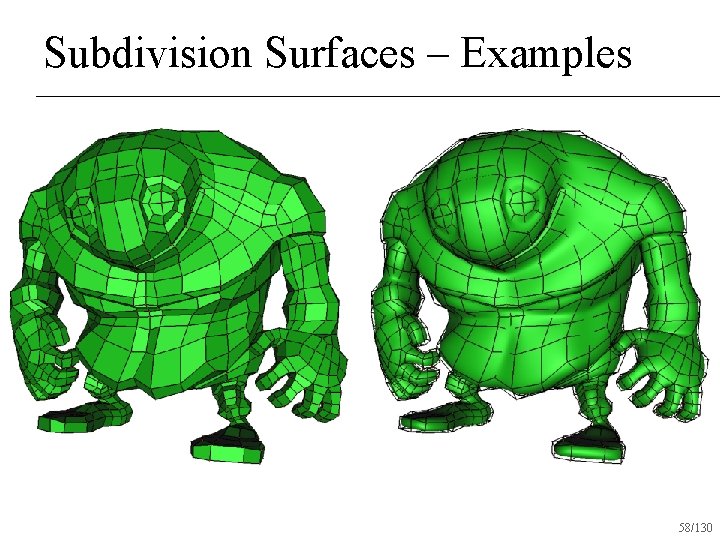
Subdivision Surfaces – Examples 58/130
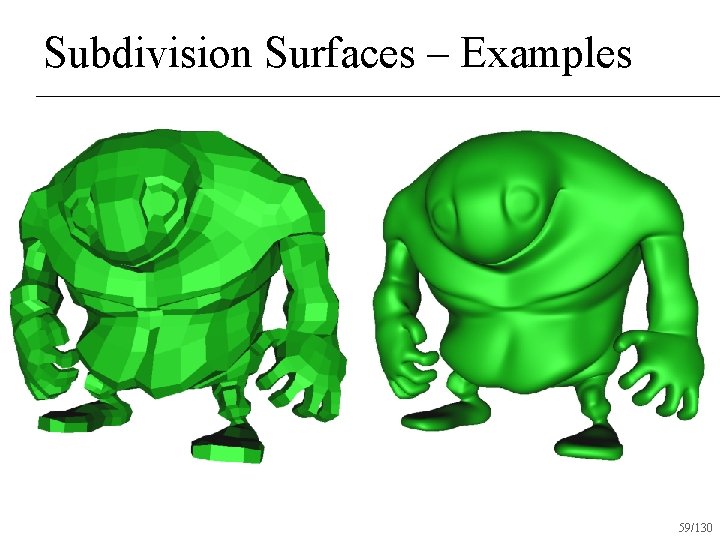
Subdivision Surfaces – Examples 59/130
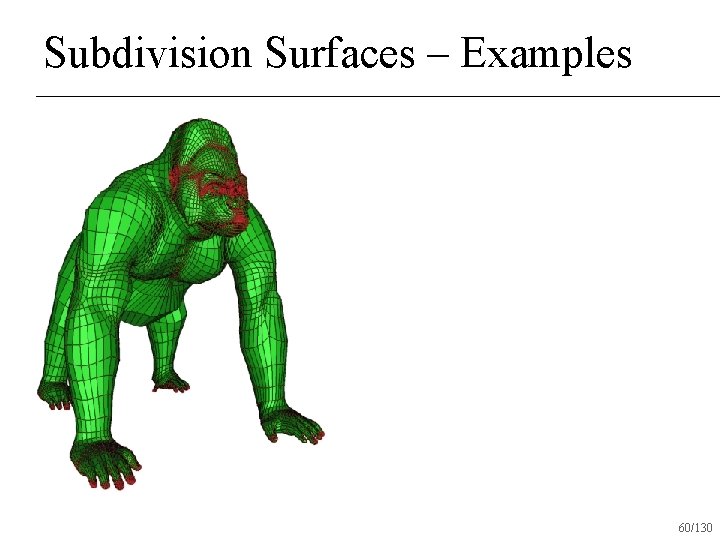
Subdivision Surfaces – Examples 60/130
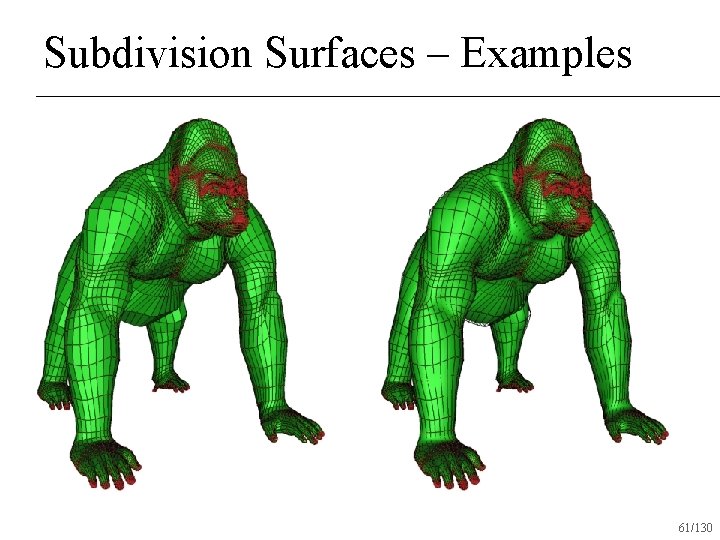
Subdivision Surfaces – Examples 61/130
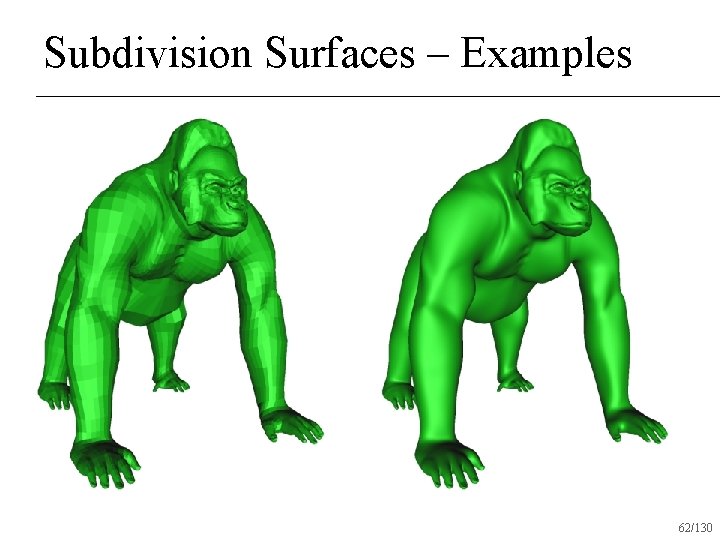
Subdivision Surfaces – Examples 62/130

Subdivision Surfaces – Examples 63/130
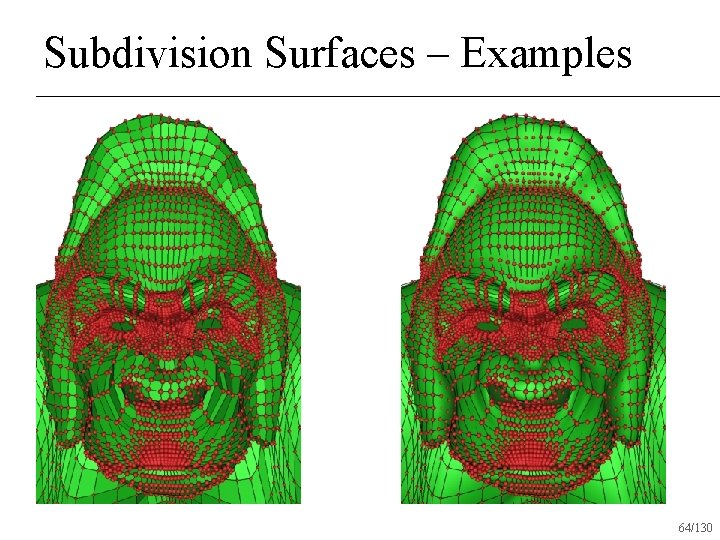
Subdivision Surfaces – Examples 64/130

Subdivision Surfaces – Examples 65/130
Catmull-Clark Subdivision 66/130
Catmull-Clark Subdivision 67/130
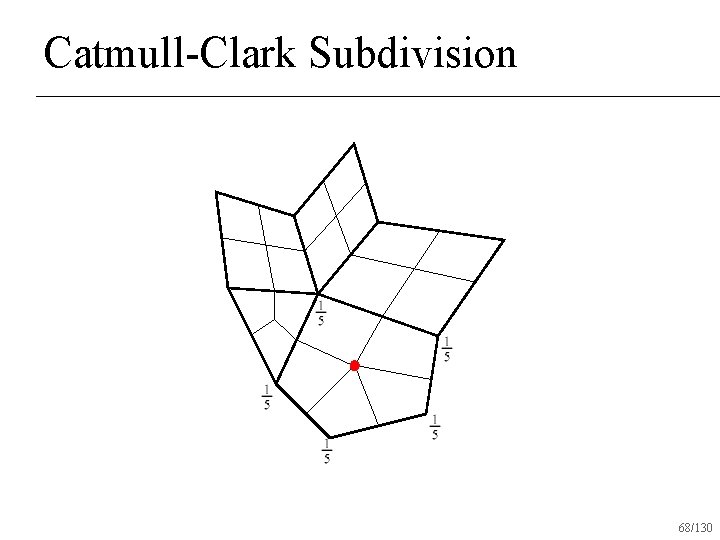
Catmull-Clark Subdivision 68/130
Catmull-Clark Subdivision 69/130
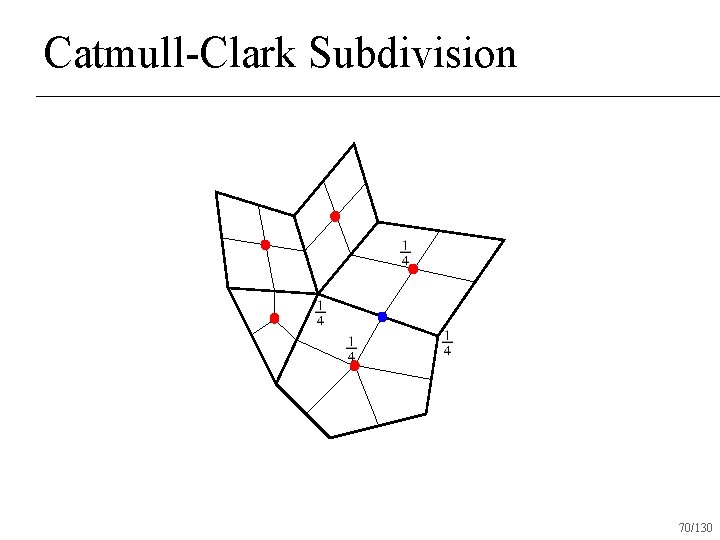
Catmull-Clark Subdivision 70/130
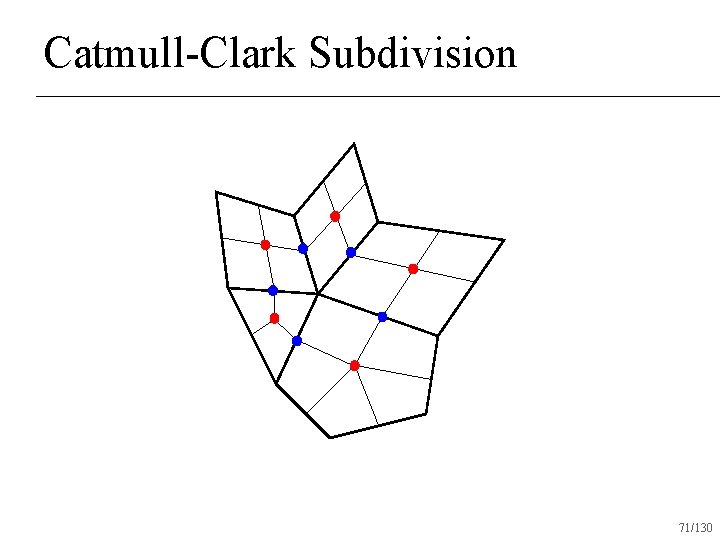
Catmull-Clark Subdivision 71/130
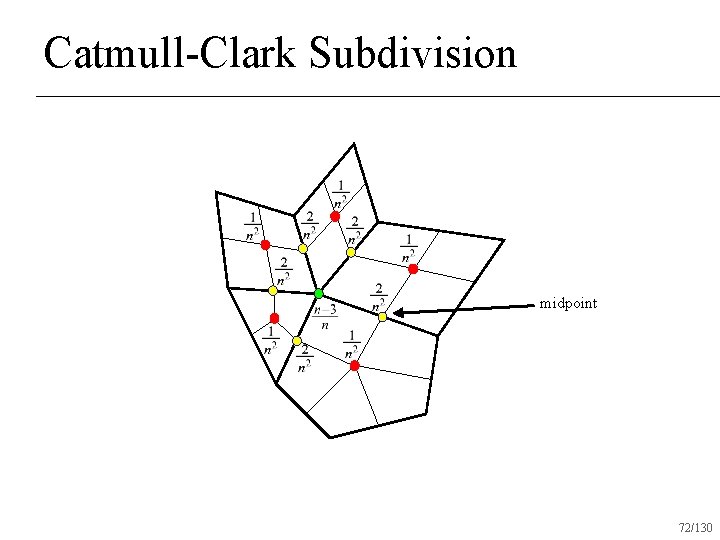
Catmull-Clark Subdivision midpoint 72/130
Catmull-Clark Subdivision 73/130

Catmull-Clark 74/130
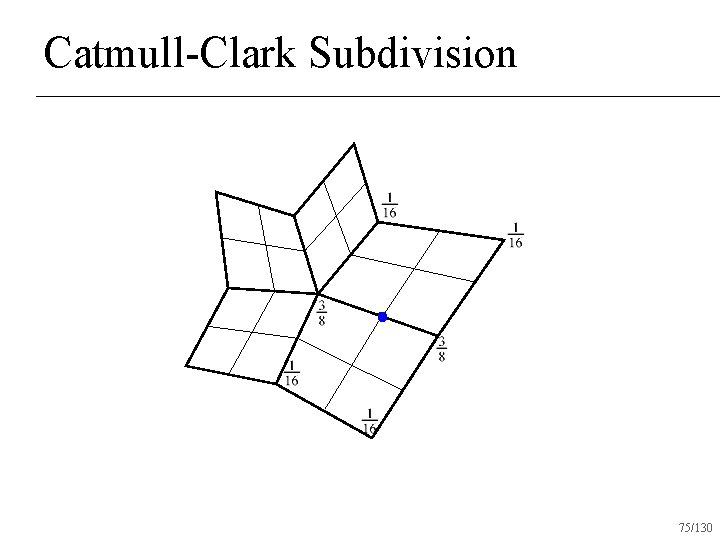
Catmull-Clark Subdivision 75/130
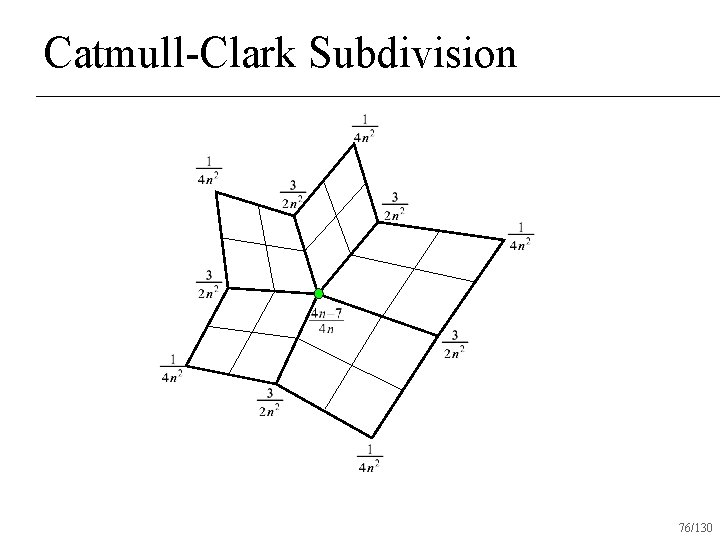
Catmull-Clark Subdivision 76/130
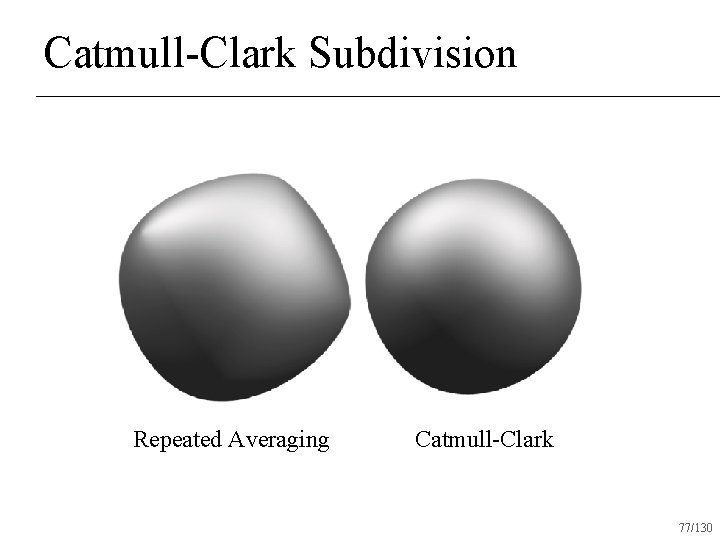
Catmull-Clark Subdivision Repeated Averaging Catmull-Clark 77/130

Catmull-Clark Subdivision One round of subdivision produces all quads n C 2 almost everywhere n C 1 at vertices with valence 4 n Most commonly used subdivision scheme in existence n 78/130
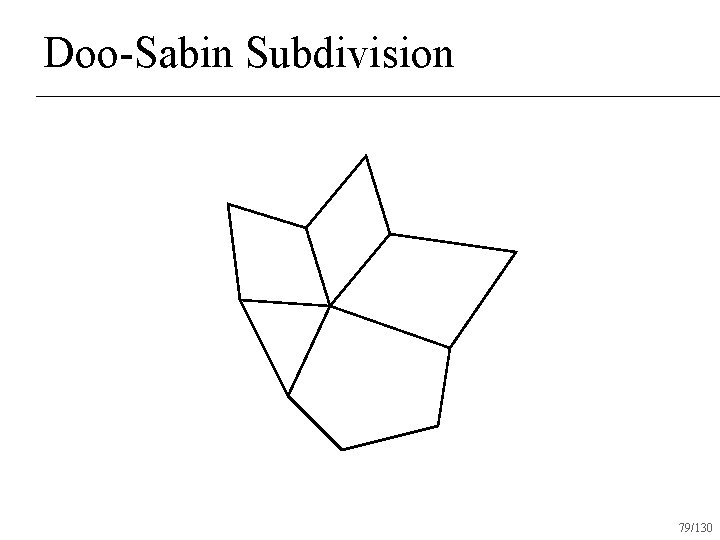
Doo-Sabin Subdivision 79/130
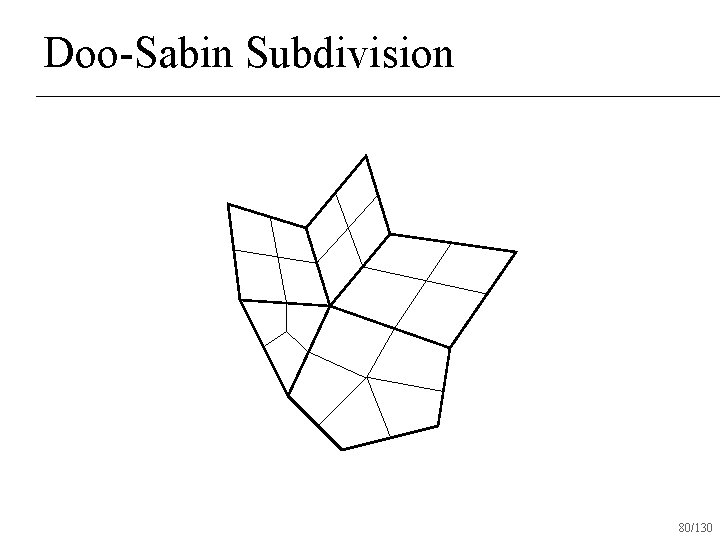
Doo-Sabin Subdivision 80/130
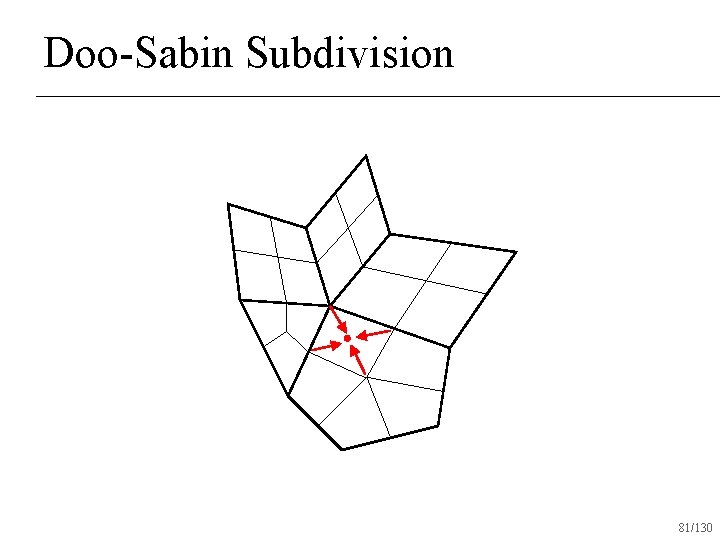
Doo-Sabin Subdivision 81/130
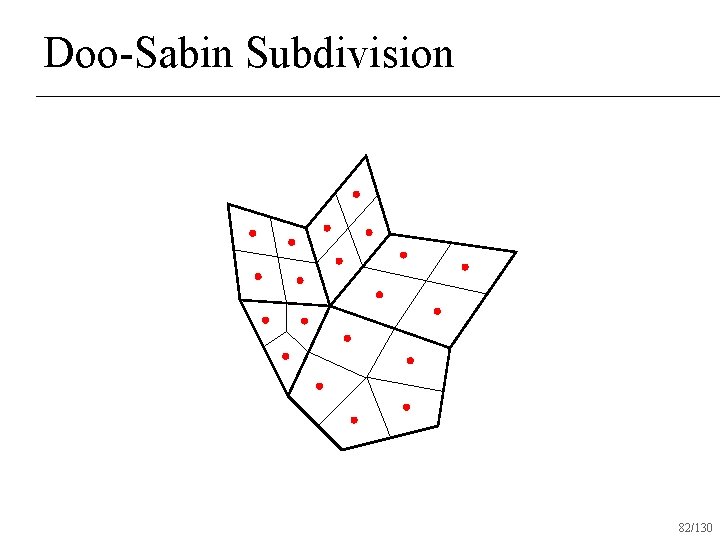
Doo-Sabin Subdivision 82/130
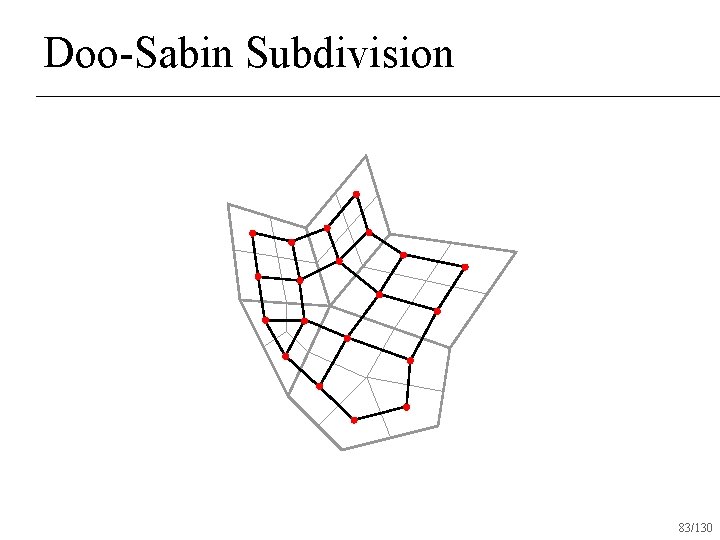
Doo-Sabin Subdivision 83/130

Doo-Sabin Subdivision Variant of repeated averaging subdivision n All vertices valence 4 after one round of subdivision n C 1 everywhere n 84/130
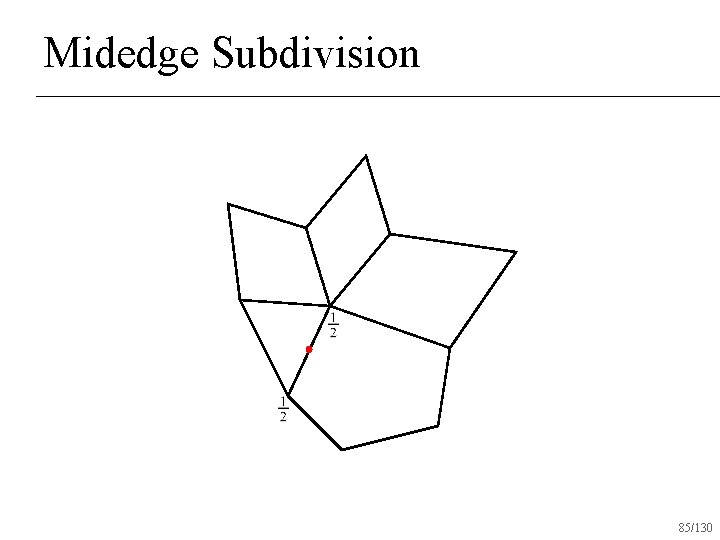
Midedge Subdivision 85/130
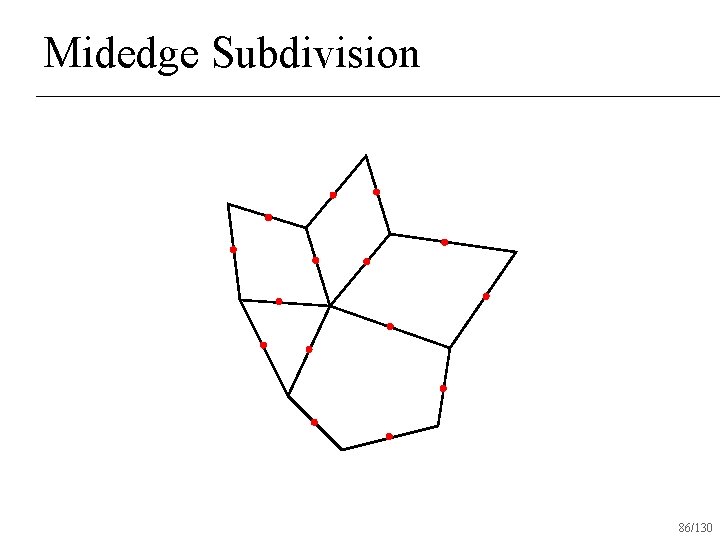
Midedge Subdivision 86/130
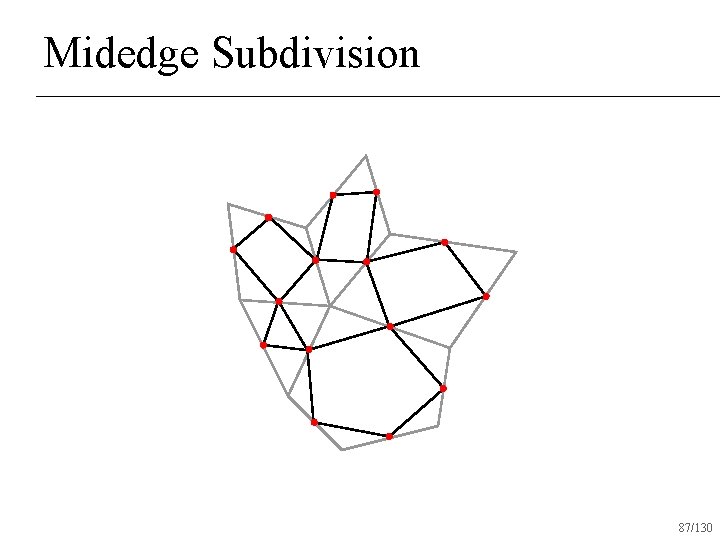
Midedge Subdivision 87/130
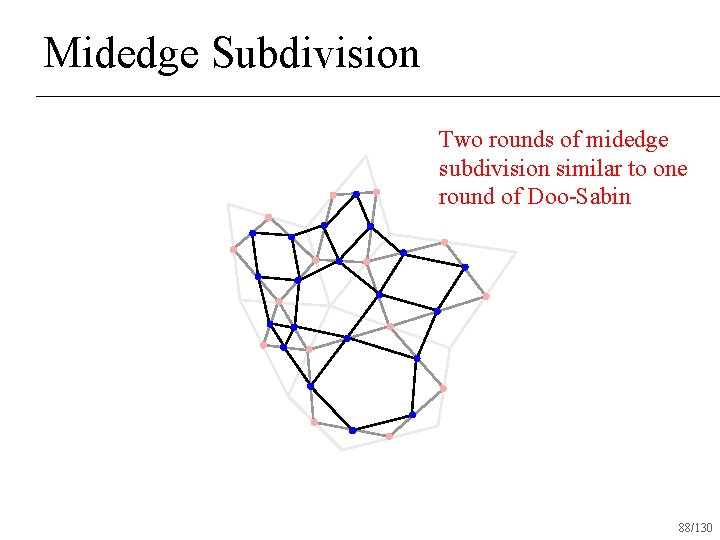
Midedge Subdivision Two rounds of midedge subdivision similar to one round of Doo-Sabin 88/130

Midedge Subdivision Simplest subdivision scheme in terms of rules (midpoint) n Produces C 1 surfaces everywhere n Very slow convergence at high valence vertices and fast convergence at low valence vertices creates artifacts n 89/130
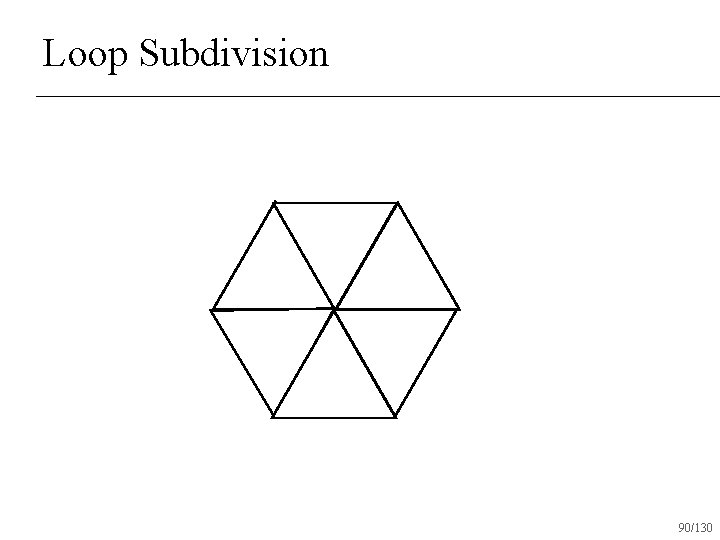
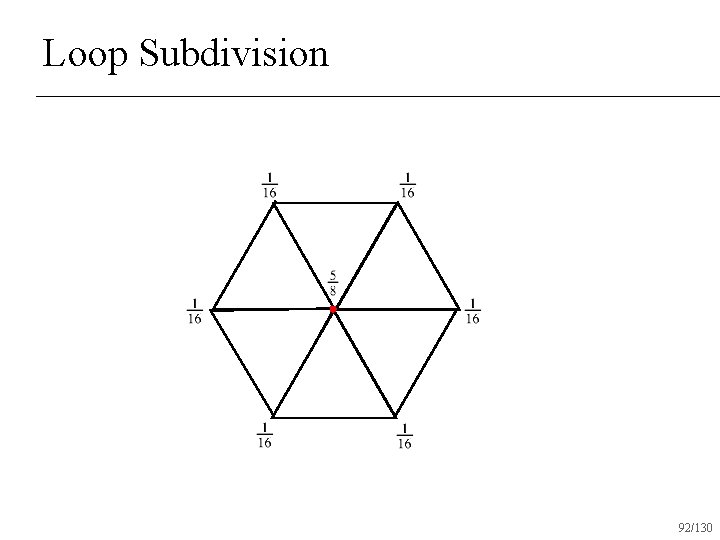
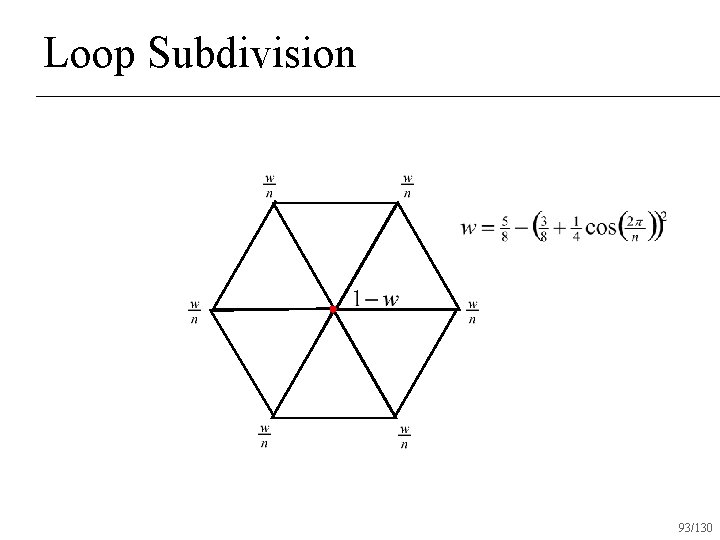
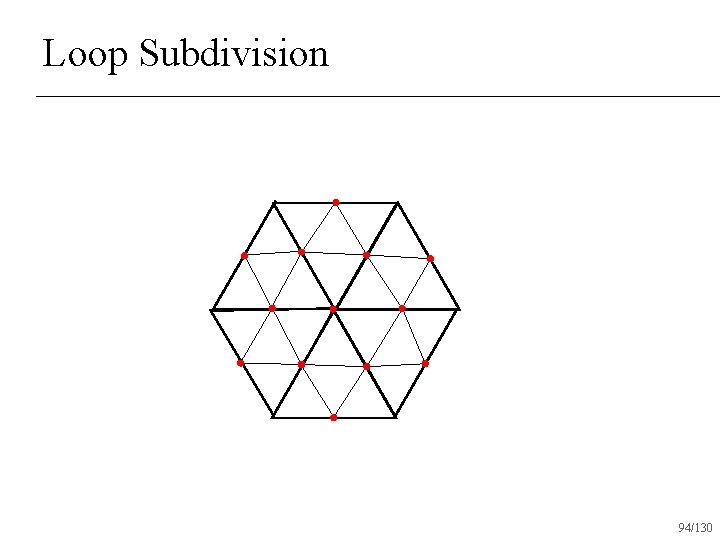
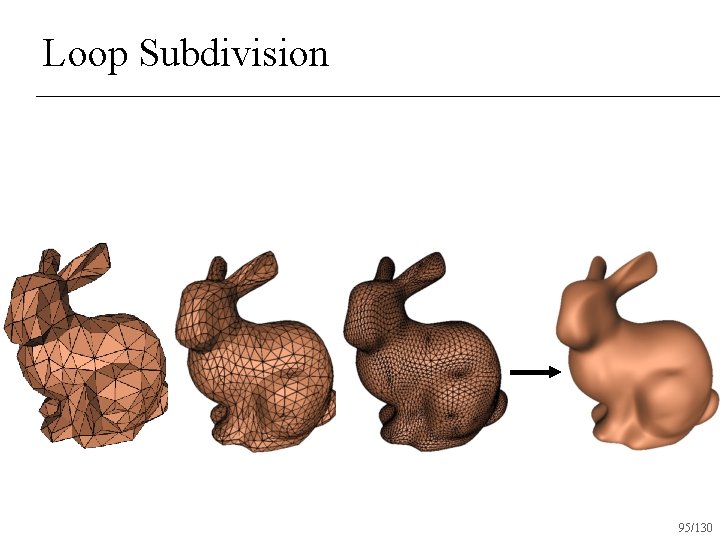
Loop Subdivision 90/130

Loop Subdivision 91/130
Loop Subdivision 92/130
Loop Subdivision 93/130
Loop Subdivision 94/130
Loop Subdivision 95/130
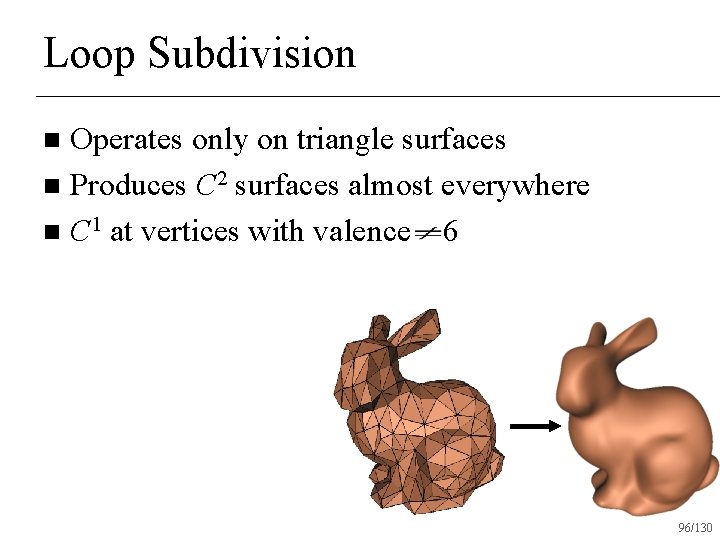
Loop Subdivision Operates only on triangle surfaces n Produces C 2 surfaces almost everywhere n C 1 at vertices with valence 6 n 96/130
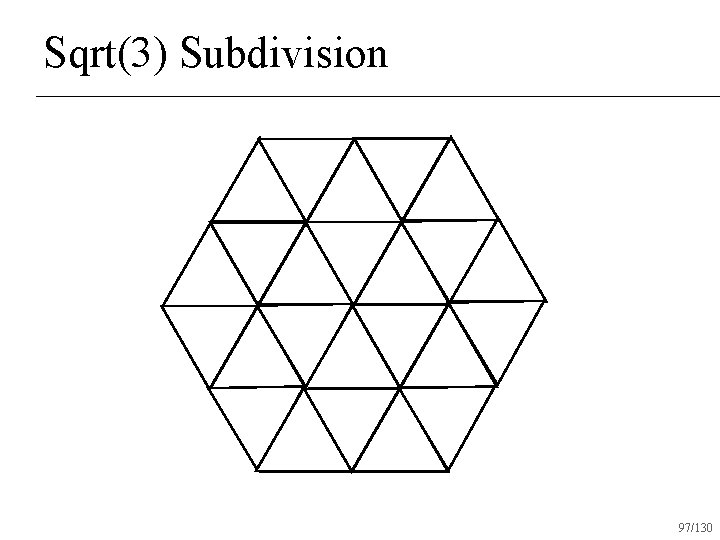
Sqrt(3) Subdivision 97/130
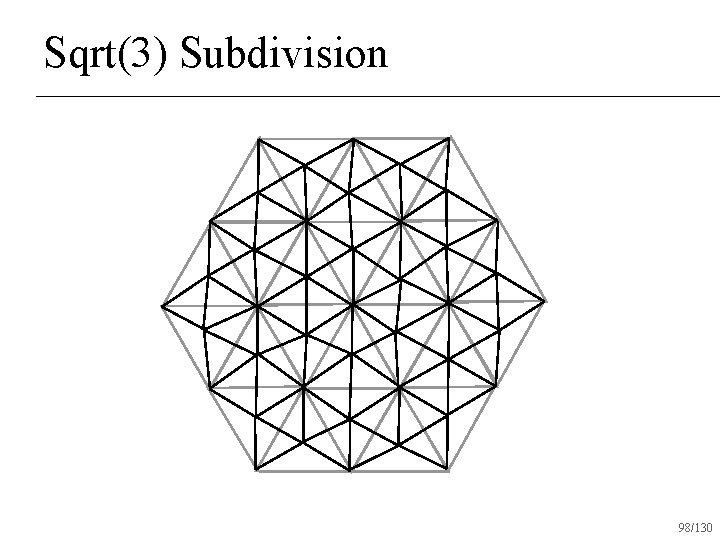
Sqrt(3) Subdivision 98/130
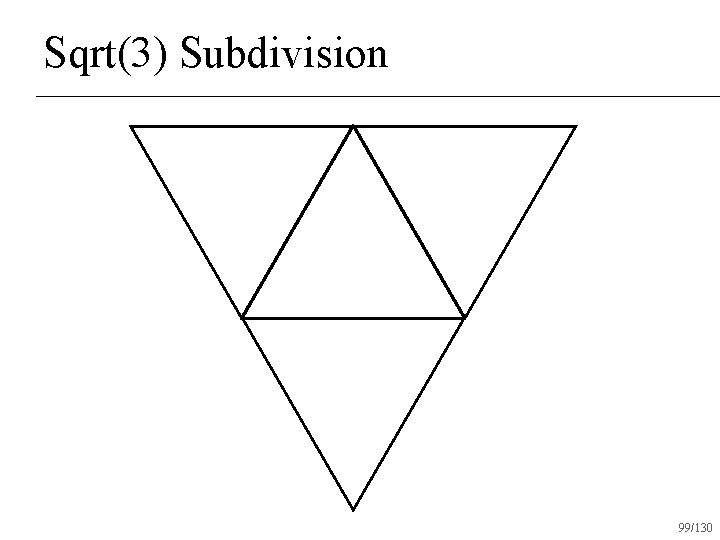
Sqrt(3) Subdivision 99/130

Sqrt(3) Subdivision 100/130
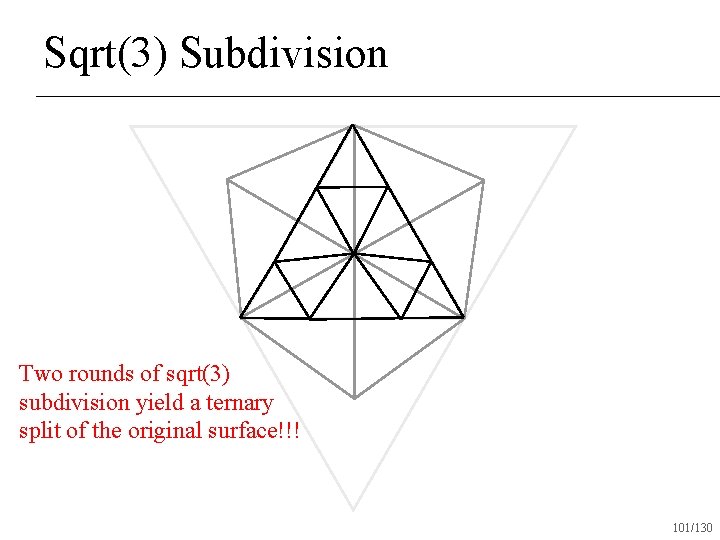
Sqrt(3) Subdivision Two rounds of sqrt(3) subdivision yield a ternary split of the original surface!!! 101/130
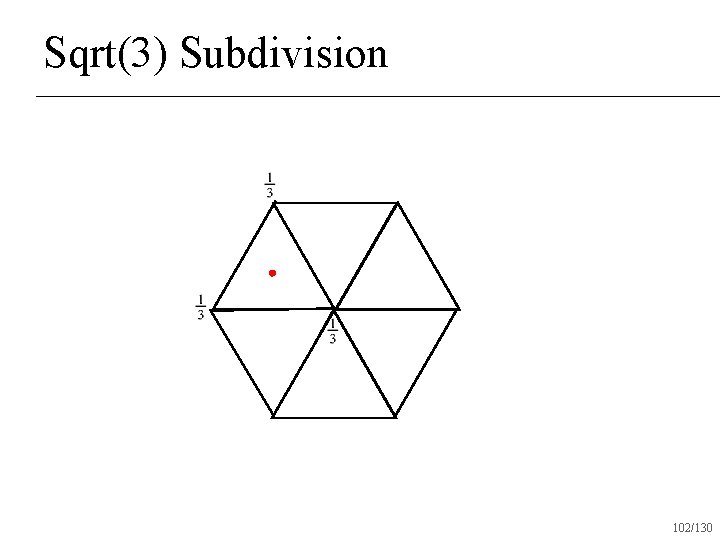
Sqrt(3) Subdivision 102/130
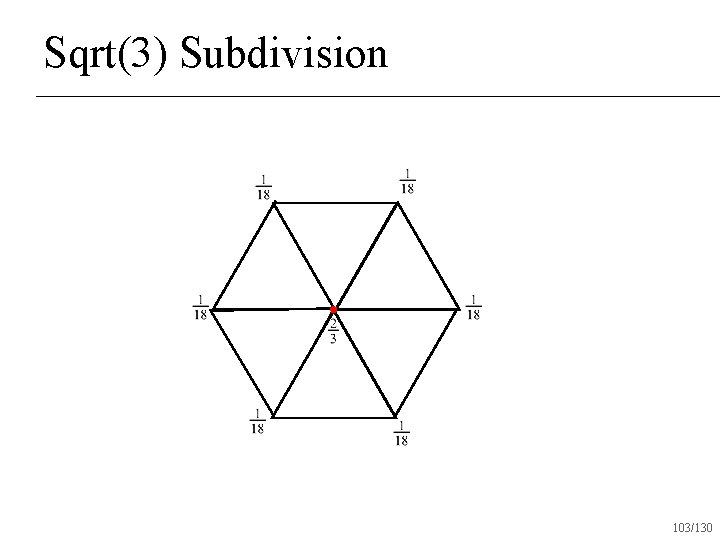
Sqrt(3) Subdivision 103/130
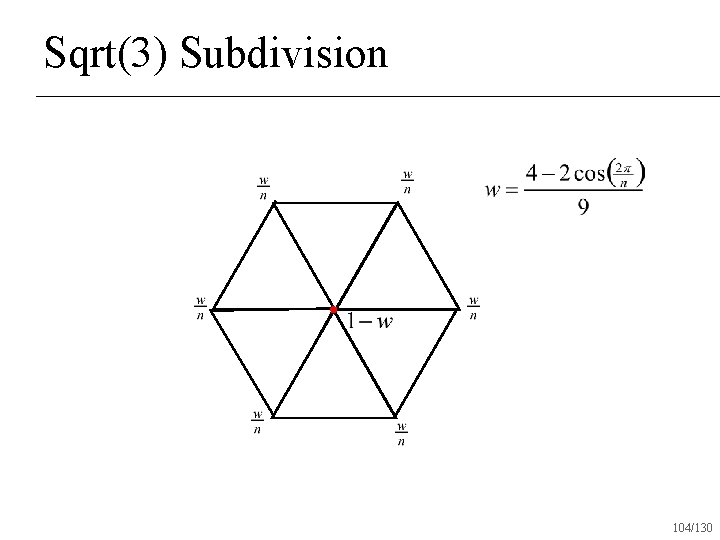
Sqrt(3) Subdivision 104/130

Sqrt(3) Subdivision Produces all triangles after one round of subdivision n Creates C 2 surfaces almost everywhere n C 1 at vertices with valence 6 n 105/130
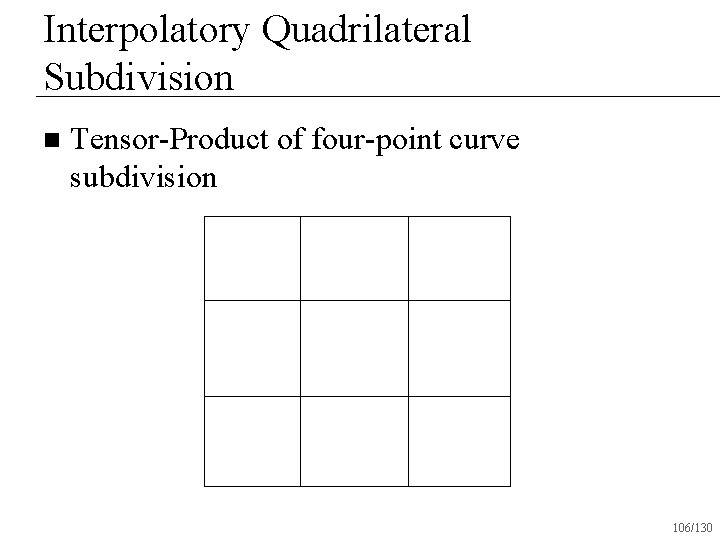
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 106/130
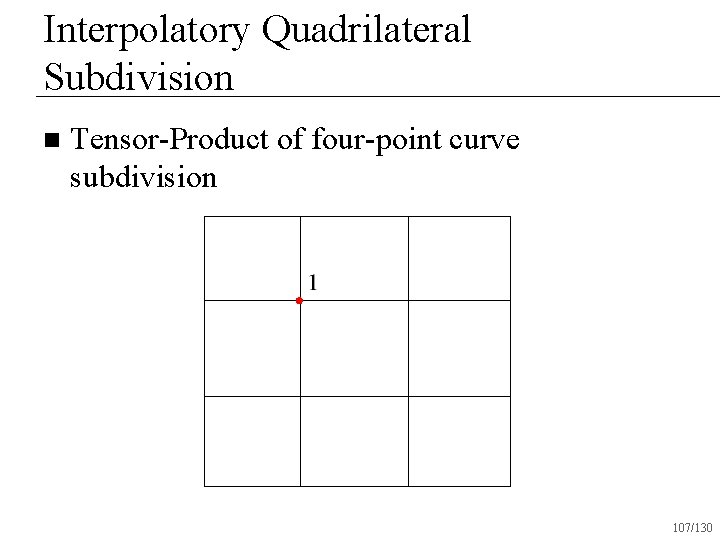
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 107/130
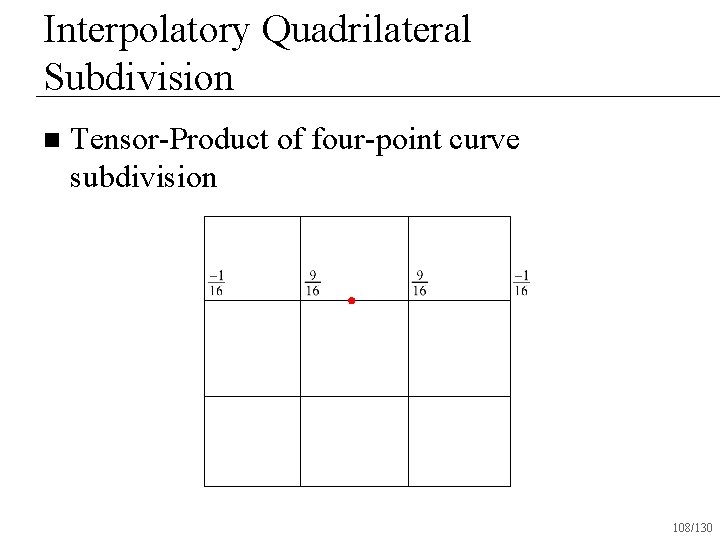
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 108/130
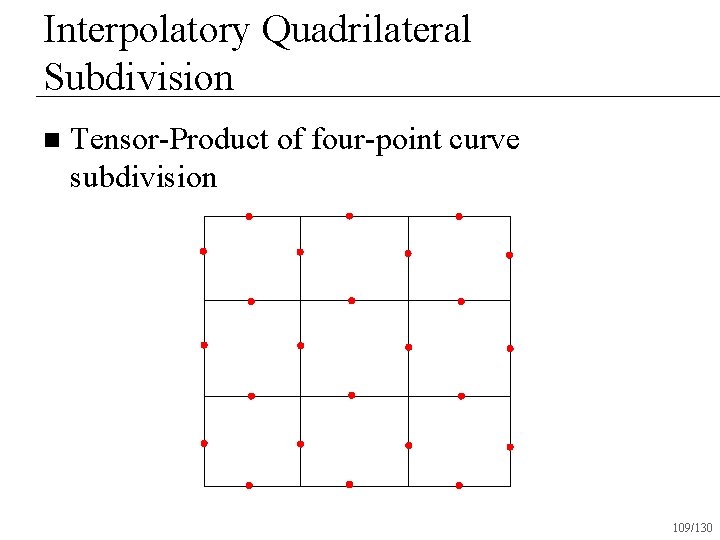
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 109/130
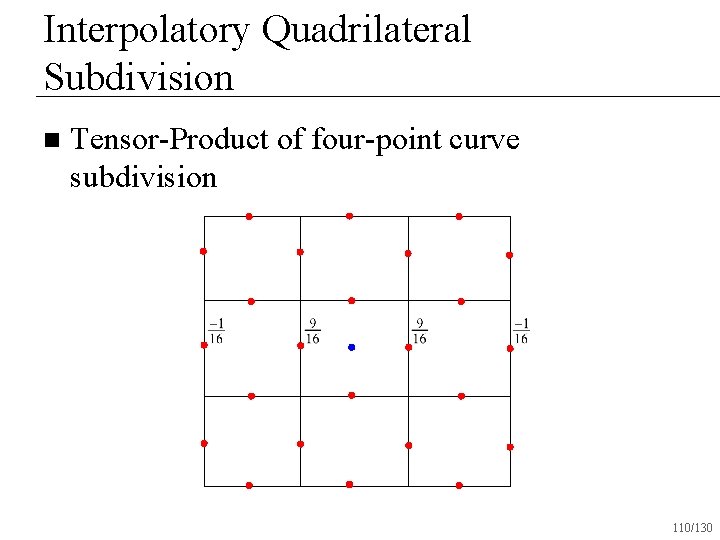
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 110/130
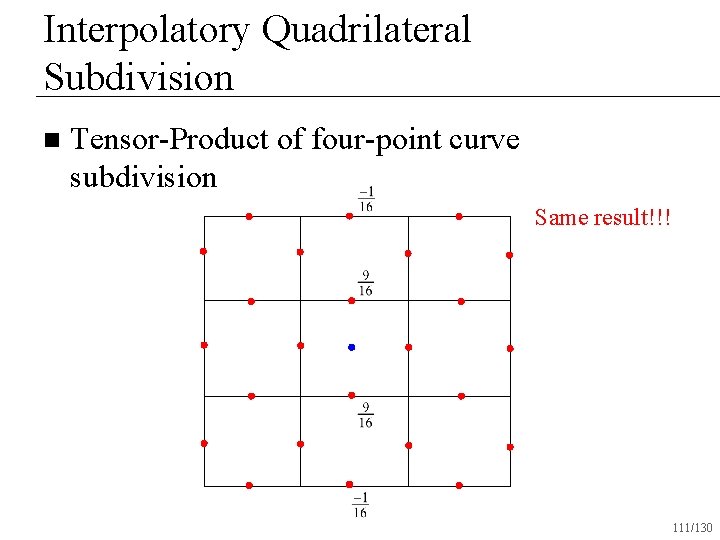
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision Same result!!! 111/130
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 112/130
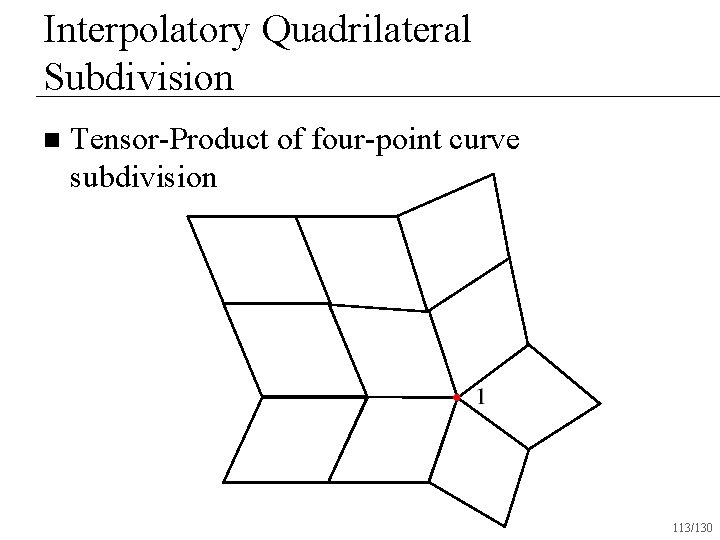
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 113/130
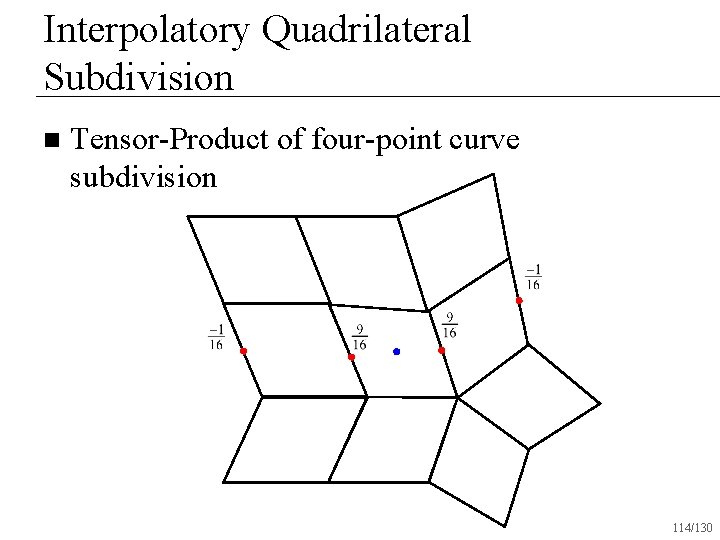
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 114/130
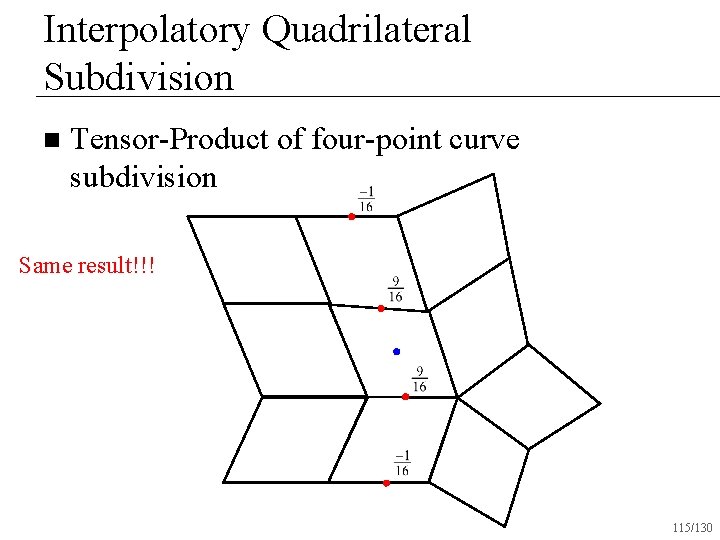
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision Same result!!! 115/130
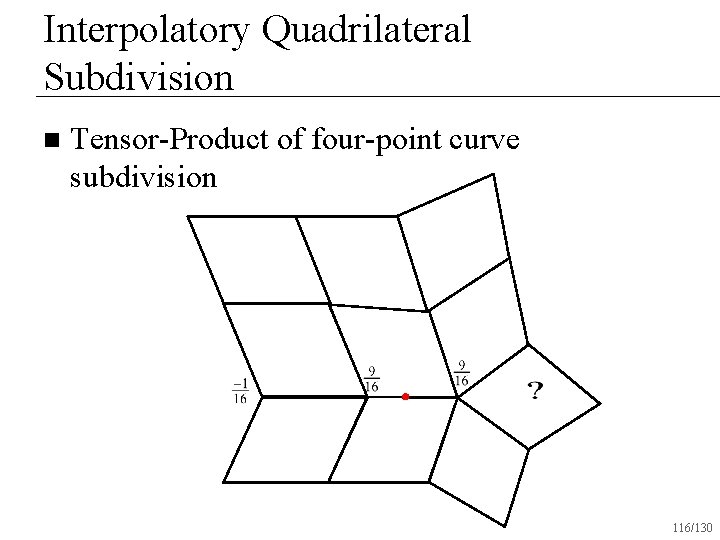
Interpolatory Quadrilateral Subdivision n Tensor-Product of four-point curve subdivision 116/130
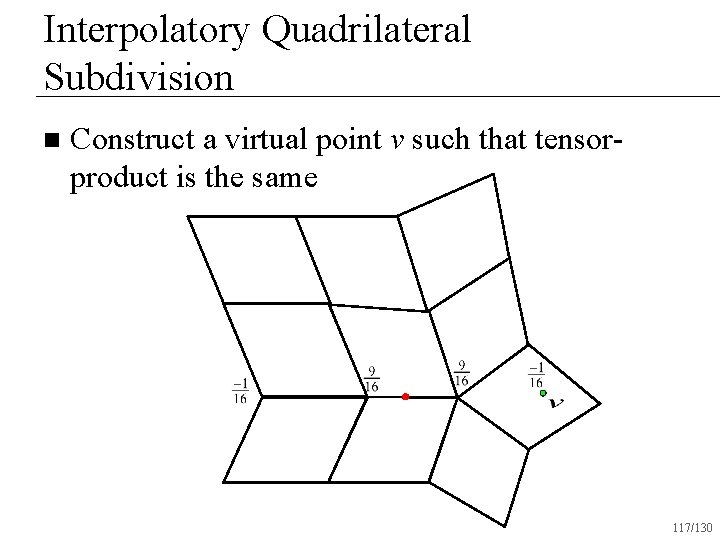
Interpolatory Quadrilateral Subdivision n Construct a virtual point v such that tensorproduct is the same 117/130

Interpolatory Quadrilateral Subdivision n Construct a virtual point v such that tensorproduct is the same 118/130

Interpolatory Quadrilateral Subdivision Based on four-point curve subdivision n Interpolates vertices n Operates only on quadrilateral surfaces n Creates C 1 surfaces everywhere n 119/130
Butterfly Subdivision 120/130
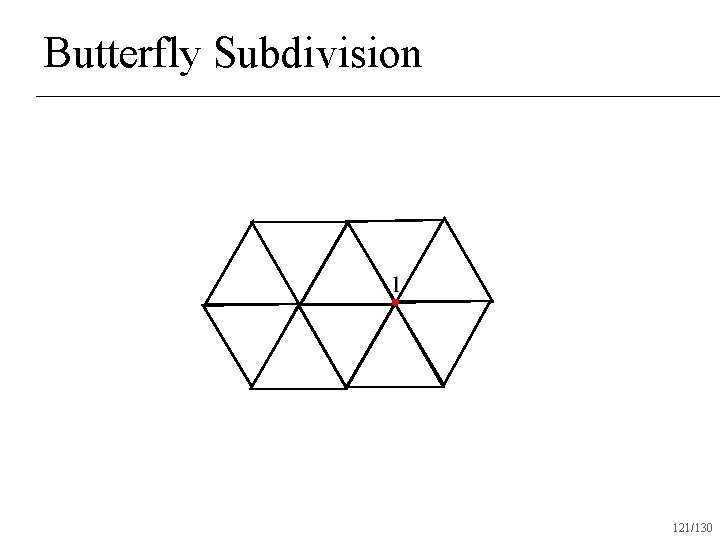
Butterfly Subdivision 121/130
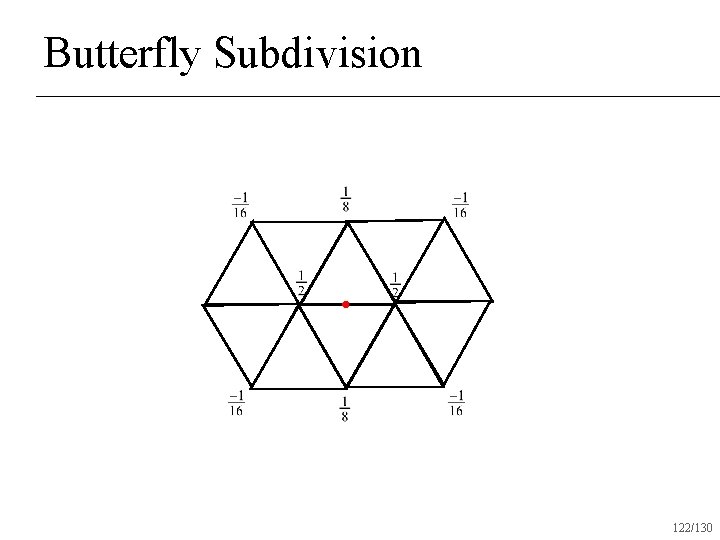
Butterfly Subdivision 122/130
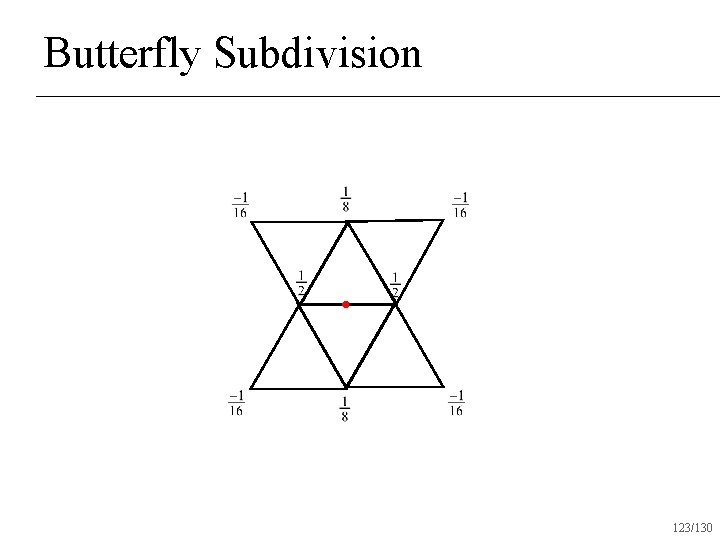
Butterfly Subdivision 123/130
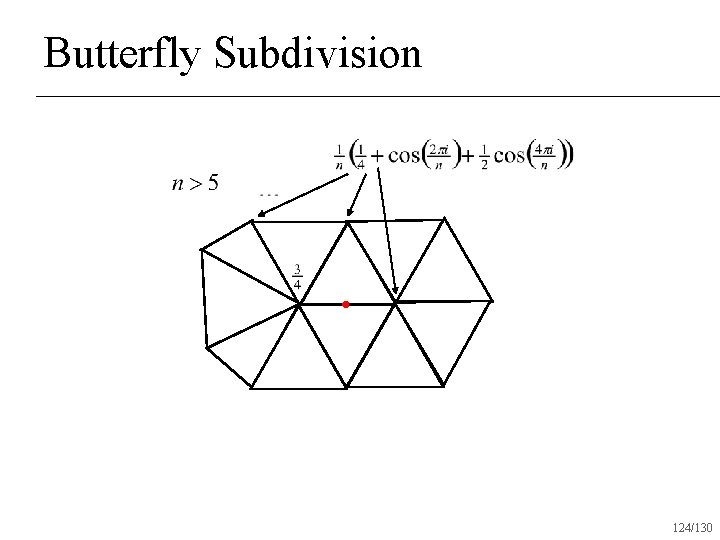
Butterfly Subdivision 124/130

Butterfly Subdivision 125/130
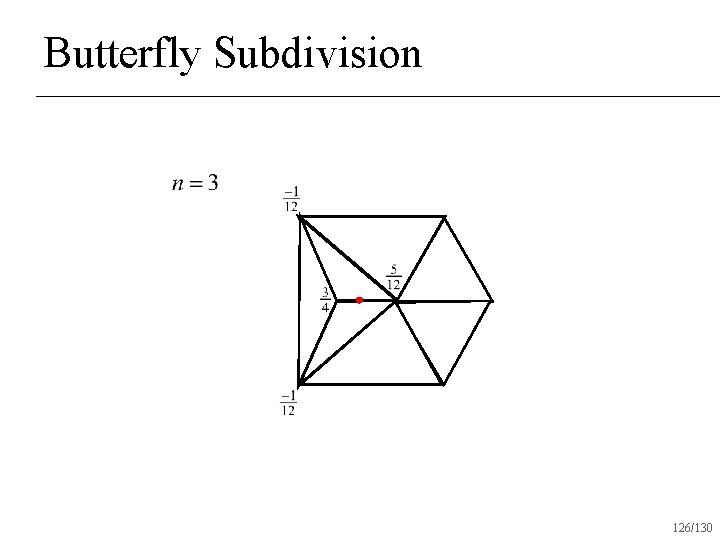
Butterfly Subdivision 126/130

Butterfly Subdivision Interpolatory subdivision scheme for triangle meshes n Produces surfaces that are C 1 everywhere n 127/130
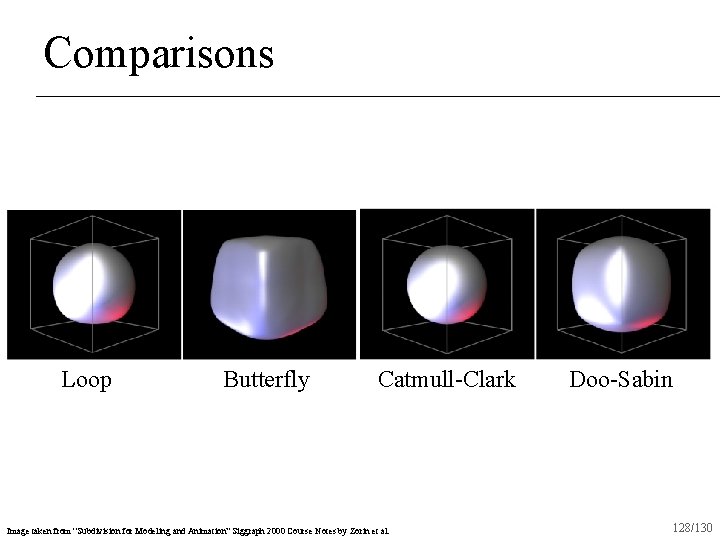
Comparisons Loop Butterfly Catmull-Clark Image taken from “Subdivision for Modeling and Animation” Siggraph 2000 Course Notes by Zorin et al. Doo-Sabin 128/130

Comparisons Loop Butterfly Catmull-Clark Image taken from “Subdivision for Modeling and Animation” Siggraph 2000 Course Notes by Zorin et al. Doo-Sabin 129/130

Comparisons Mesh Loop Catmull-Clark (triangulated) Image taken from “Subdivision for Modeling and Animation” Siggraph 2000 Course Notes by Zorin et al. 130/130
- Slides: 130