Suatu Matriks Pangkat Suatu Matriks Nilai yang menunjukkan

Suatu Matriks

Pangkat Suatu Matriks Nilai yang menunjukkan ukuran (dimensi) suatu matriks yang determinannya tidak samadengan nol. Nilai pangkat didasarkan pada dimensi terbesar untuk determinan tidak samadengan nol. Bila pangkat tersebut diperoleh dari beberapa anak-matriks, maka pangkat matriks ditentukan oleh determinan anak-matriks yang tidak samadengan nol.

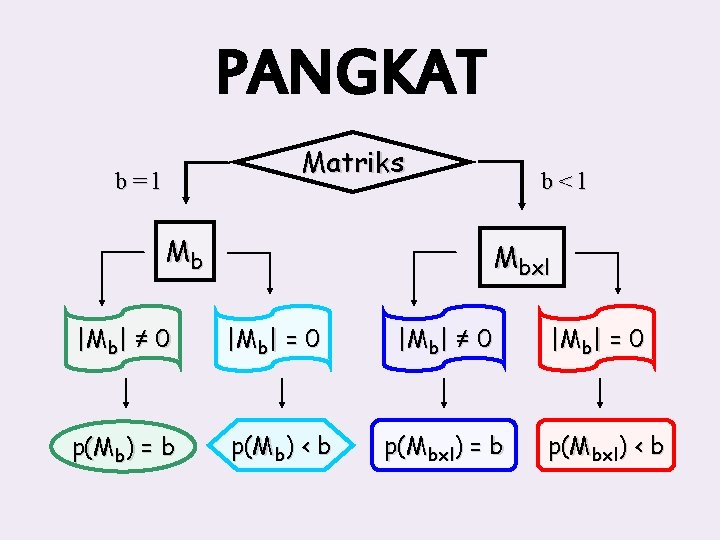
PANGKAT Matriks b=l Mb b<l Mbxl | M b| ≠ 0 | M b| = 0 p(Mb) = b p(Mb) < b |Mb| ≠ 0 p(Mbxl) = b | M b| = 0 p(Mbxl) < b

Cara pengolahan : Perhatikan dimensi matriks. Hitung determinannya. Penyelesaian : a. Algoritma b. Minor-kofaktor c. Penyapuan Bila diperoleh determinannya = 0, lanjutkan ke dimensi berikutnya atau ke dimensi yang lebih rendah (kecil). Tentukan pangkatnya. Nilai pangkat didasarkan pada dimensi tertinggi untuk determinan ≠ 0.

CL P 01 SL P 01 1. Tentukan pangkat kedua matriks segi berikut : A = 1 2 -1 5 -1 -2 11 4 -5 B = 2 -1 1 1 -1 JCL P 01 -1 2. Tentukan pangkat kedua matriks tak segi berikut : C= 0 -5 -8 4 -1 -3 2 2 3 1 D= 5 2 4 4 1 3 1 1 1 2 5 3 JCL P 01 -2

JCL P 01 -1 : A = (3 x 3) 1 2 5 -1 11 4 -1 -2 -5 Penyelesaian : (algoritma) Hitung determinannya : | A | = {(1)(-5) + (2)(-2)(11) + (-1)(4)(5)} – {(-1)(11) + (2)(5)(-5) + (1)(4)(-2)} = – 12 Tentukan pangkatnya : berpangkat penuh | A | = -12 ≠ 0 (sesuai dgn dimensi) (3 x 3) p(A) = 3

B = 2 -1 (3 x 3) -1 -1 1 1 -1 Penyelesaian : (algoritma) Hitung determinannya : | B | = {(2)(-1) + (-1)(1)(1) + (1)(1)(-1)} – {(1)(-1)(1) + (-1)(-1) + (2)(1)(1)} = 0

Periksa : 2 -1 1 -1 | B 11 | = (2)(-1) – (-1) = – 3 Tentukan pangkatnya : | B | = 0 ; | B 11 | = -3 ≠ 0 (2 x 2) (3 x 3) p(B) = 2

JCL P 01 -2 : C= 0 -5 -8 4 -1 -3 2 2 3 1 Langkah pertama; dengan mengubahnya menjadi 2 matriks segi berdimensi 3 x 3 C 1 = 0 -5 -8 4 -1 -3 2 C 2 = 4 -1 -3 2 2 3 1

Penyelesaian C 1 : (algoritma) Hitung determinannya : | C 1 | = {(0)(-1)(2) + (4)(3)(-8) + (2)(-3)(-5)} – {(2)(-1)(-8) + (4)(-5)(2) + (0)(-3)(3)} = – 42 Tentukan pangkatnya : | C 1 | = -24 ≠ 0 ; (3 x 3) p(C) = 3

D= 5 2 4 4 1 3 1 1 1 2 5 3 Langkah pertama; dengan mengubahnya menjadi 2 submatriks segi berdimensi 3 x 3 D 1 = 5 2 4 4 1 3 1 1 1 D 2 = 4 1 3 1 1 1 2 5 3

Penyelesaian D 1 : (algoritma) Hitung determinannya : | D 1 | = {(5)(1)(1) + (4)(1)(4) + (1)(3)(2)} – {(1)(1)(4) + (4)(2)(1) + (5)(3)(1)} = 0 | D 2 | = {(4)(1)(3) + (1)(5)(3) + (2)(1)(1)} – {(2)(1)(3) + (1)(1)(3) + (4)(1)(5)} = 0 Langkah kedua; karena determinan keduanya = 0, maka periksa untuk dimensi 2 x 2 terhadap matriks D tsb.

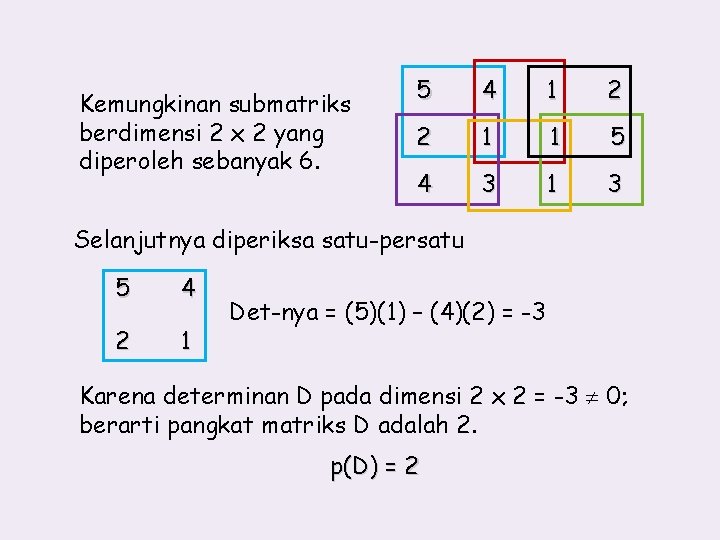
Kemungkinan submatriks berdimensi 2 x 2 yang diperoleh sebanyak 6. 5 4 1 2 2 1 1 5 4 3 1 3 Selanjutnya diperiksa satu-persatu 5 4 2 1 Det-nya = (5)(1) – (4)(2) = -3 Karena determinan D pada dimensi 2 x 2 = -3 0; berarti pangkat matriks D adalah 2. p(D) = 2