SU 2 YangMills eos with fluctuating Temperature Tams




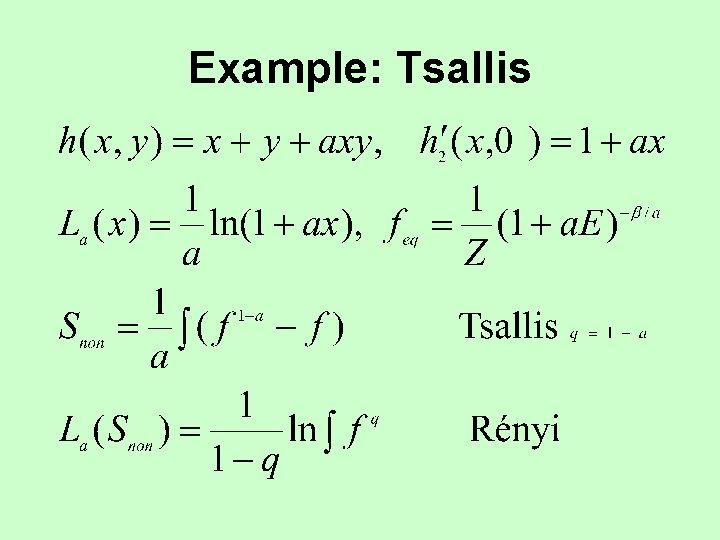










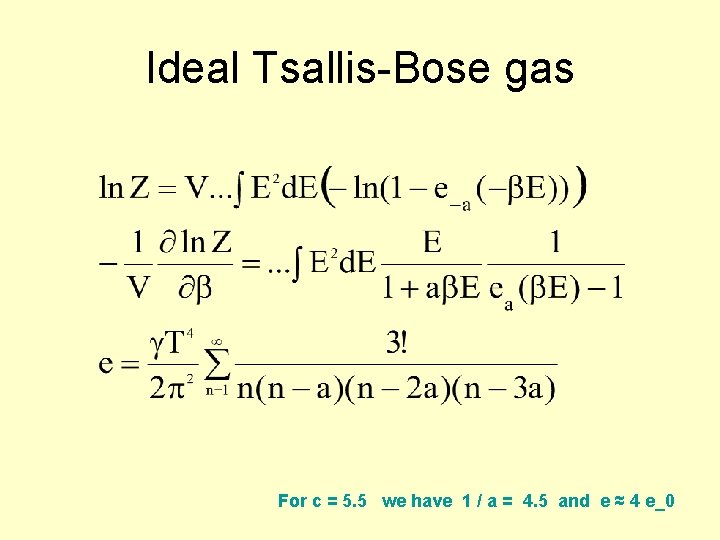

- Slides: 32

SU 2 Yang-Mills eos with fluctuating Temperature Tamás S. Bíró (KFKI RMKI Budapest / ELTE) and Zsolt Schram (DTP ATOMKI Debrecen) 1. Superstatistics: Euler-Gamma T 2. Monte Carlo with rnd. spacing 3. Ideal gas limit, effective action 4. Numerical results for SU 2 Non-Perturbative Methods in Quantum Field Theory, 10 -12. 03. 2010 Hévíz, Hungary

Entropy formulas, distributions

Laws of thermodynamics 0. Equilibrium temperature ; entanglement 1. T d. Y(S) = d. X(E) + p d. U(V) - µ d. Z(N) 2. d. S ≥ 0 3. S = 0 at T = 0 4. thermodynamical limit: associative composition rule

Example: Gibbs-Boltzmann
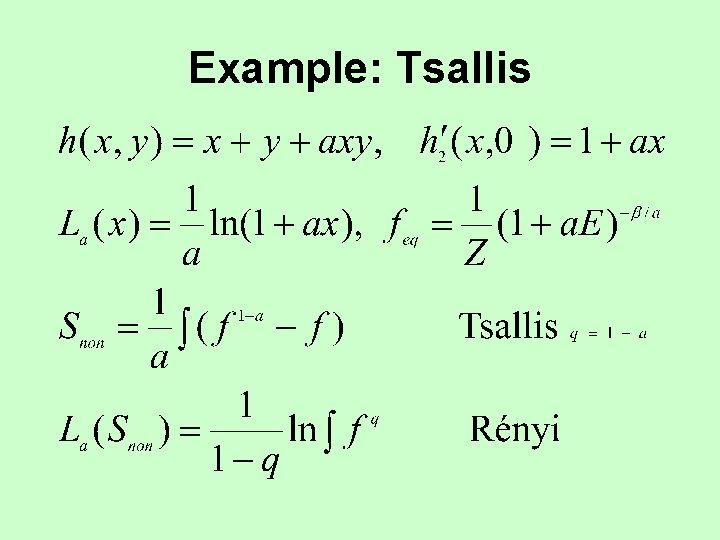
Example: Tsallis

Compisition in small steps: e ic t o m y s a pt l ru

3. Possible causes for non-additivity a. Long range interaction energy not add. b. Long range correlation entropy not add. c. Example: kinetic energy composition rule for massless partons with E - dependent interaction

Superstatistics a. Kinetic simulation (NEBE) b. Monte Carlo simulation c. Superstatistics: effective partition function

Canonical distribution: POWER – LAW TAILED q = 1 + 1 / c -(c+1) f exp( - U / T ) = ( 1 + E / c. T ) This equals to Gamma distributed Gibbs factors: -(c+1) (1+x/c) Interpretations: 1 = (c+1) c -t -xt/c dt t e e fluctuating temperature, energy imbalance, multiplicative + additive noise, . . .

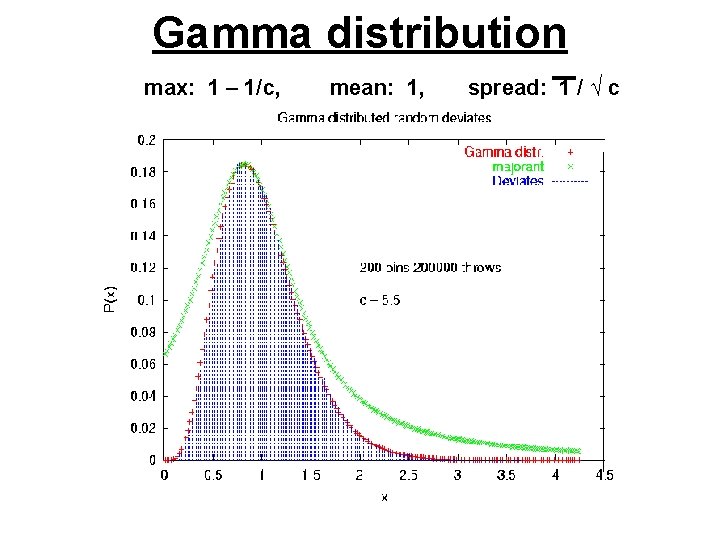
Gamma distribution max: 1 – 1/c, mean: 1, spread: 1 / √ c

Fluctuating spacing Expectation values of observables: A = ∫ DU∫ dt wc (t) ∫DU∫ dt wc (t) -S(t, U) e v t A(U) -S(t, U) e Action: S(t, U) = a(U) t + b(U) / t t = a t / as asymmetry parameter

Effective action method Effective action calculation: ∫ DU A = ∫ DU e-S eff (U, v) A(U) -S eff (U, 0) e v=0: Polyakov line, v=1: ss Plaquettes, v=-1: ts Plaquettes

Lattice theory: effective action ∞ Seff = - ln ∫dt 0 cc c+v-1 -(a+c)t - b/t t e (c) Plaquette sums: space-space: a = ∑ (1 – Re tr P ss space-time: b = ∑ (1 – Re tr P ts) Evaluation methods: exact analytical • saddle point • numerical (Gauss-Laguerre) •

Lattice theory: effective action Seff = cc - ln (c) ( (c+v)/2 b ) ( a+c 2 K c+v (2 b(a+c) ) ) Asymptotics: • large a, b finite c: • large a, b, c and a-b << (a+b): 2 ab a+b

Numerical results Euler Gamma distribution Near to standard: c = 1024. 0 Smaller values of c (13. 5, 5. 5) Asymmetry parameter in MC Action difference and sum -> eos Other quantities


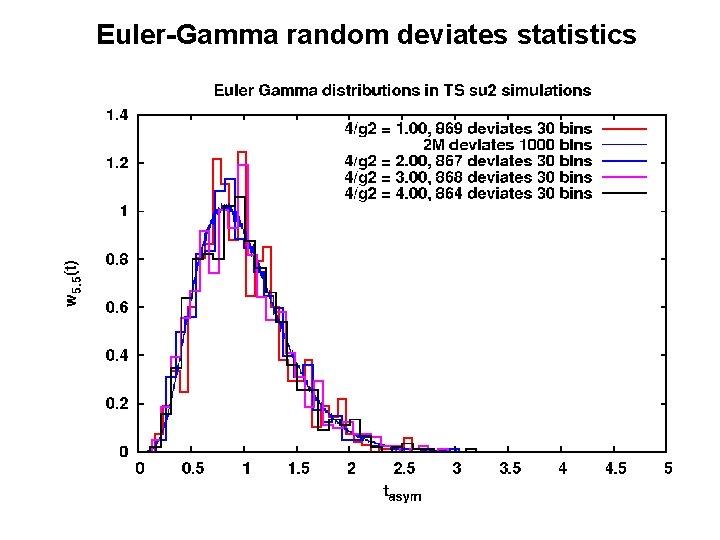
Test of Gamma deviates

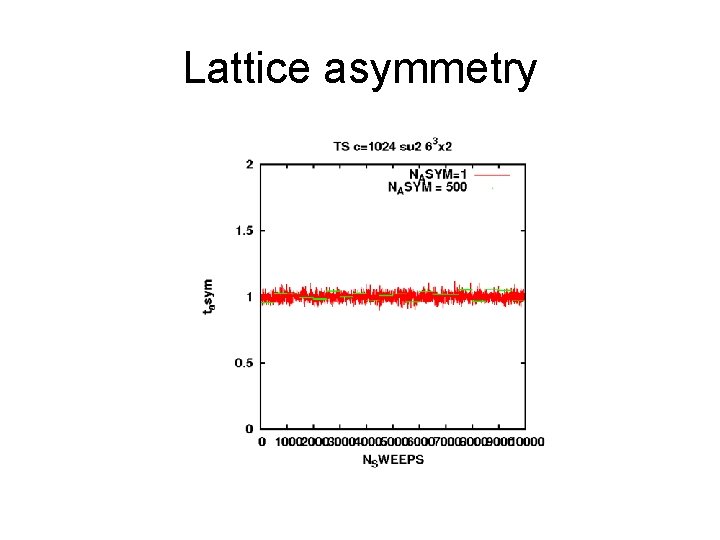
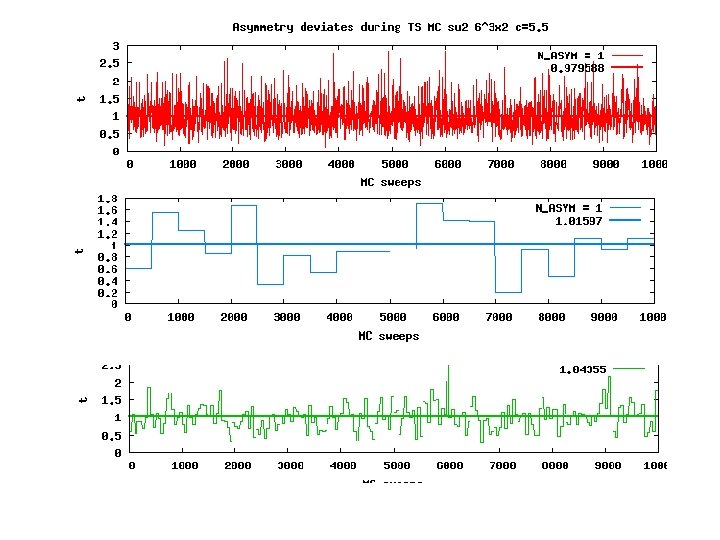
Lattice asymmetry

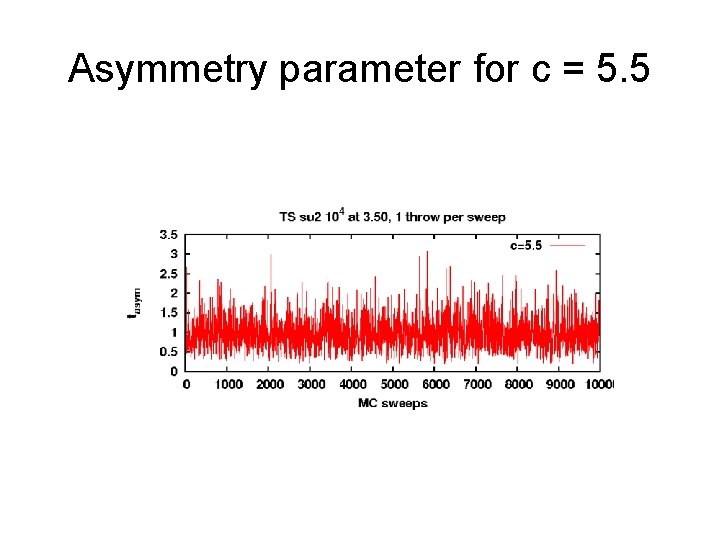
Asymmetry parameter for c = 5. 5


Euler-Gamma random deviates statistics

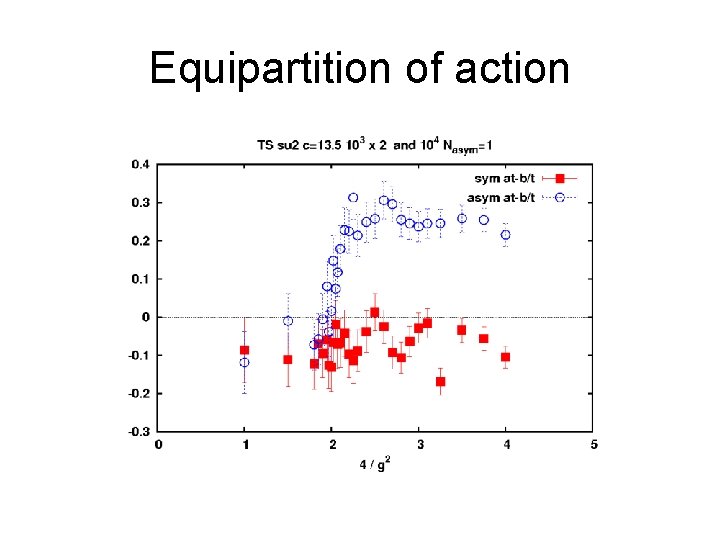
Equipartition of action

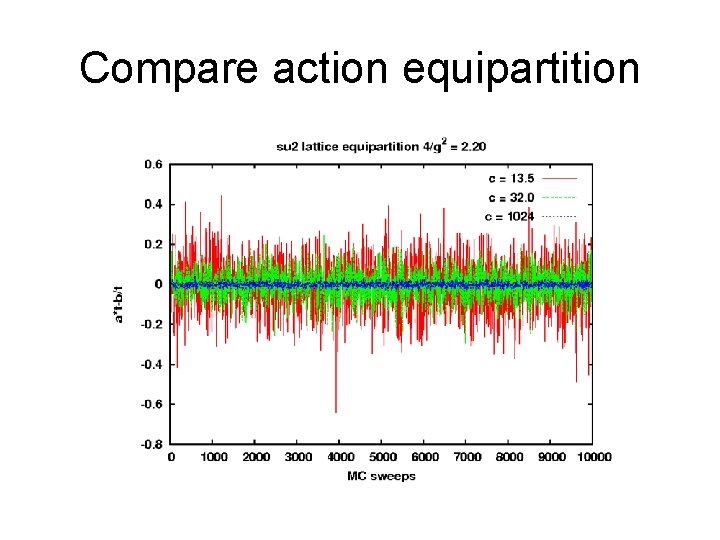
Compare action equipartition

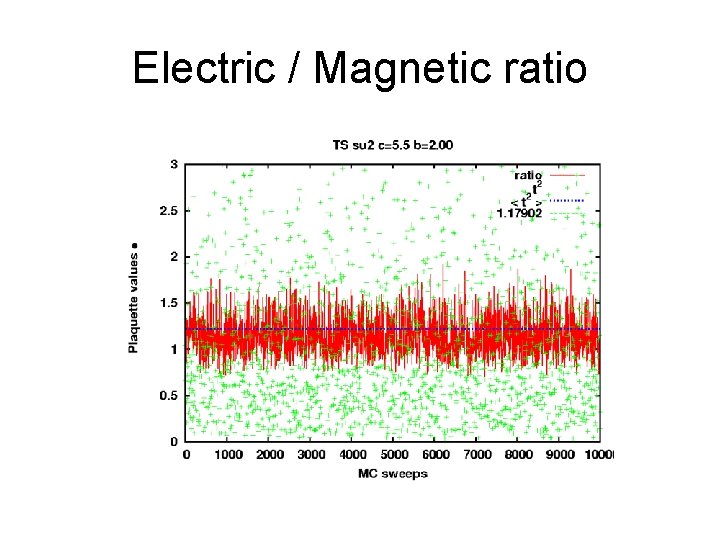
Electric / Magnetic ratio

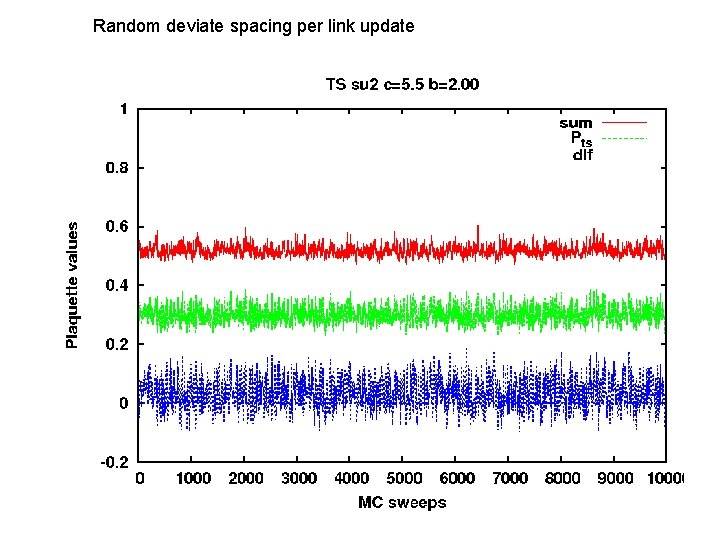
Random deviate spacing per link update

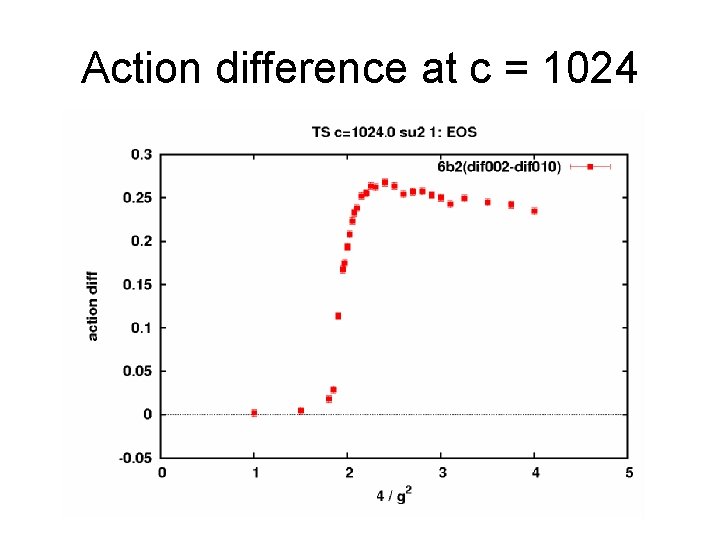
Action difference at c = 1024

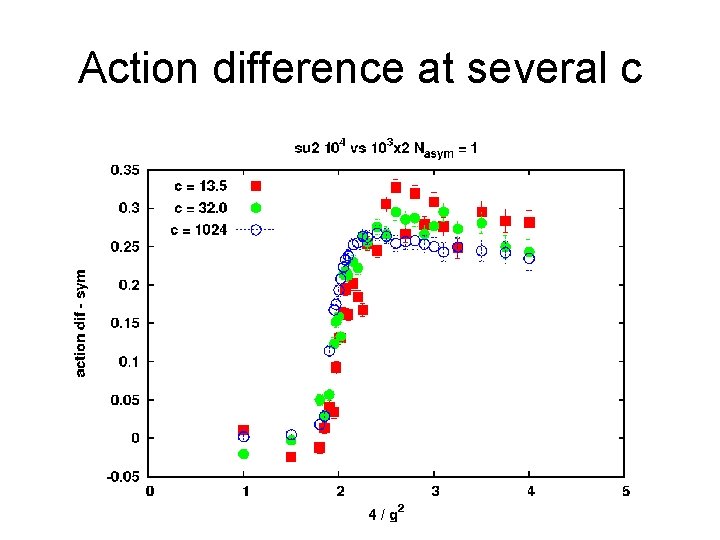
Action difference at several c

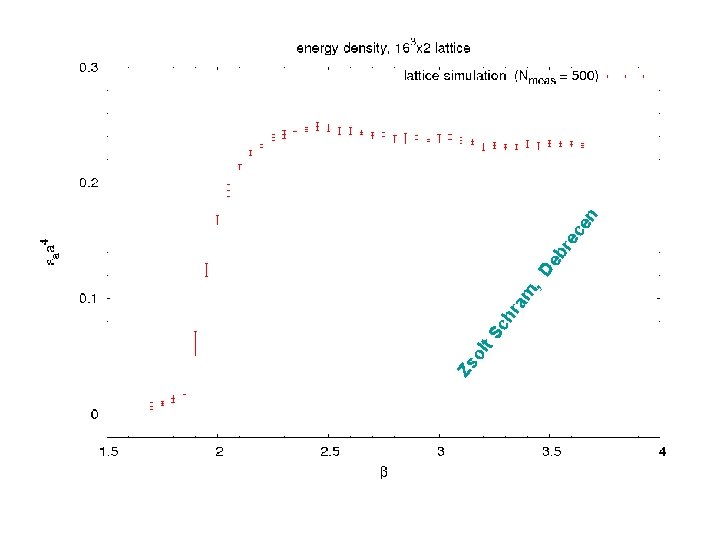
ch ra m t. S Zs ol , en ec De br
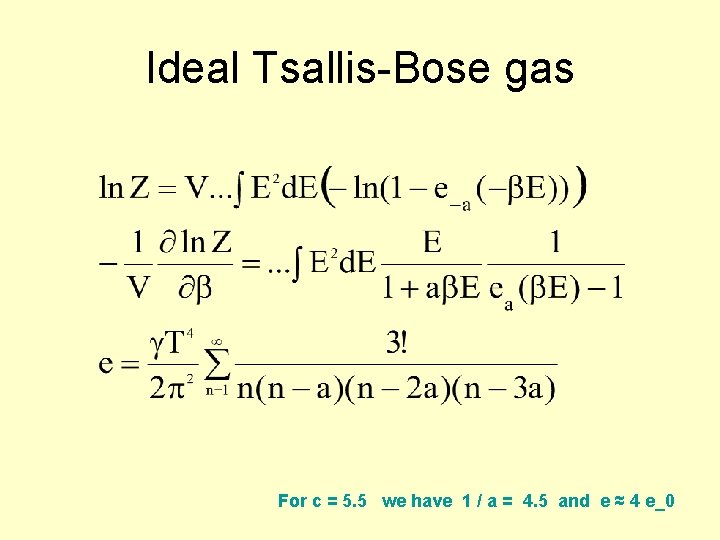
Ideal Tsallis-Bose gas For c = 5. 5 we have 1 / a = 4. 5 and e ≈ 4 e_0

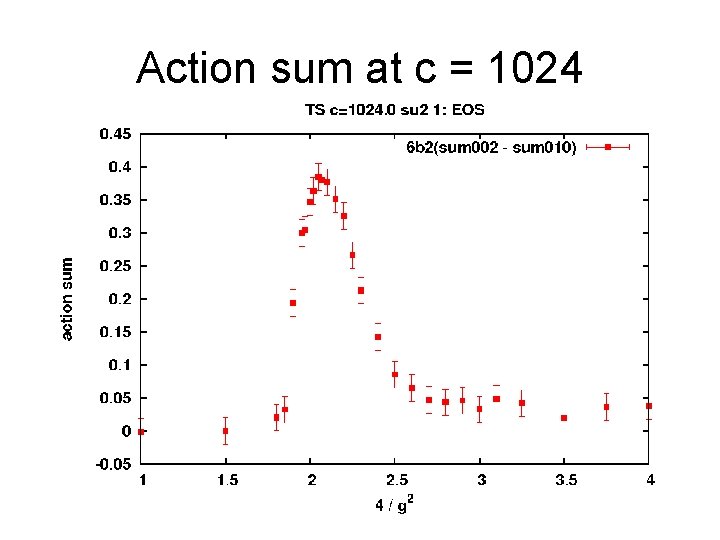
Action sum at c = 1024

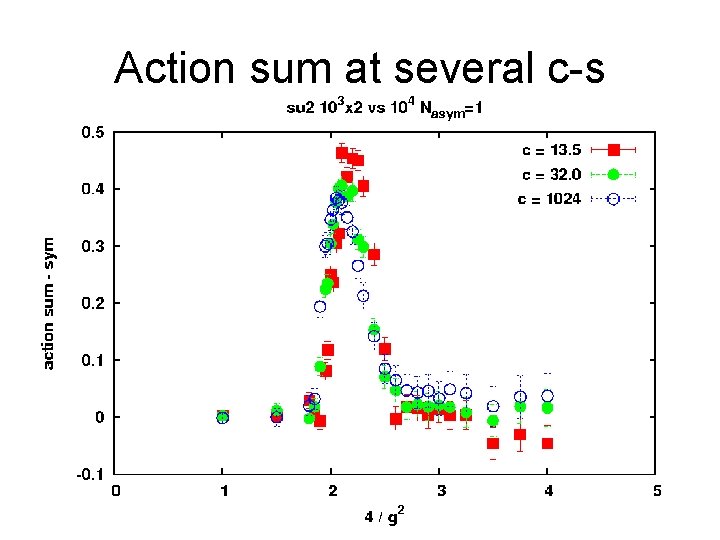
Action sum at several c-s

Composition rule entropy Power-law not exponential Superstatistics Tsallis-Bose id. gas eos SU 2 YM Monte Carlo eos