Student lab Exercises Experiencing Numerical algorithms using Mathematica

Student lab. Exercises. Experiencing Numerical algorithms using Mathematica A. S. Cvetkovic G. V. Milovanovic

Properties of numerical algorithms Numerical stability • Arithmetic operations in finite precision • Evaluation of functions in finite precision • Ill-conditioning of numerical algorithms • Complexity of numerical algorithms • Time complexity • Space complexity •

Why Mathematica • Number formats in Mathematica Exact numbers Integers: 1, -10, 0 Rational: 2/3, -1/4 Algebraic: 2, 1+ 2 transcendent: , e

Floating Point Format IEEE-754, DEC, IBM, MIL-STD-1750 Double precision 16 -decimal digits mantissa exponent part at most Arbitrary Precision Numbers Maximal number Minimal number

Topics covered • Number representations, arithmetic operations, recursive computation • Computation of transcendental functions • Construction of orthogonal polynomials • Linear algebra • Non-linear equations, polynomial equations • Interpolation problems • Approximation problems • Numerical derivation, integration • Ordinary differential equations

Structure of examples 1) Start with an obvious algorithm, which is bad for numerical purposes, to give motivation 2) Explain the reason of the poor behavior 3) Present numerical algorithm which solves the problem

Calculation of the Sin function

How does it look like

Number representation

Arithmetic operations

Transcendental functions

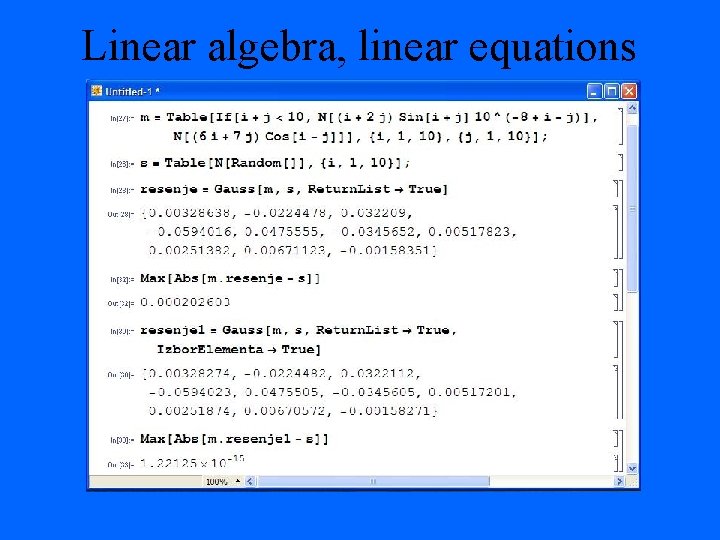
Linear algebra, linear equations

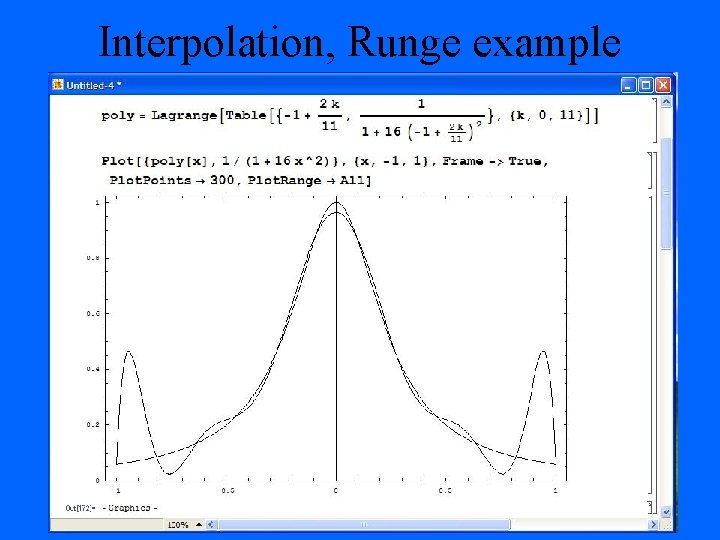
Interpolation, Runge example

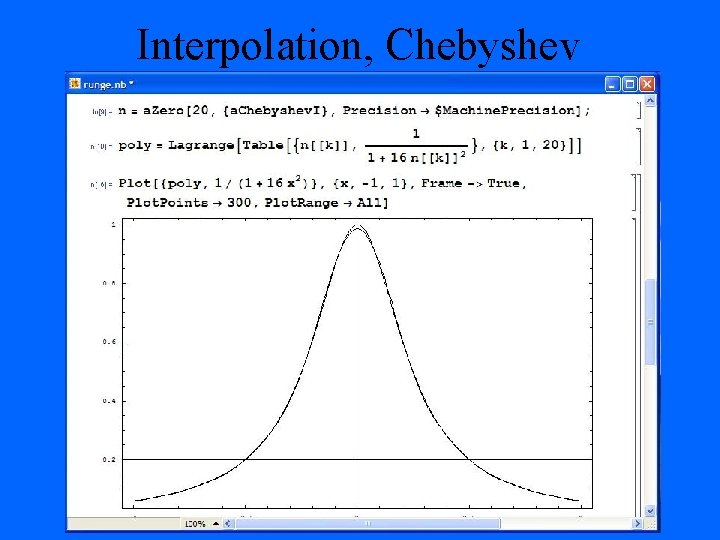
Interpolation, Chebyshev