Stud Wall Design Mahesh Dhakal mkdhakalhotmail com Stud

Stud Wall Design Mahesh Dhakal mkdhakal@hotmail. com

Stud Wall Design

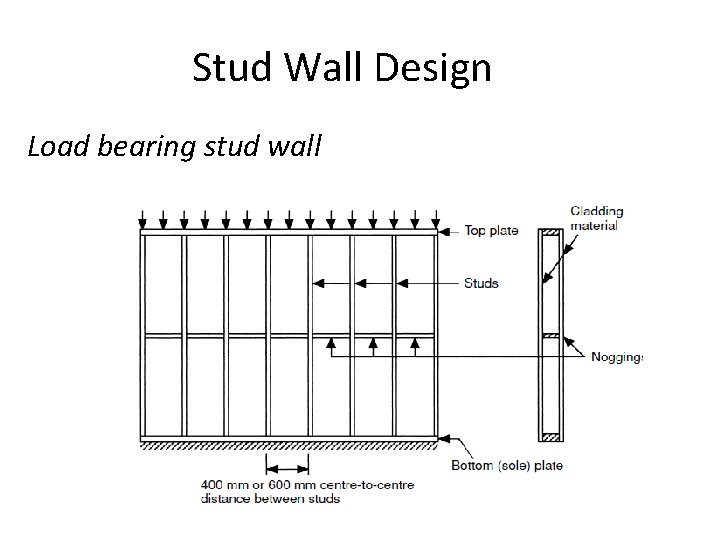
Stud Wall Design • In timber frame housing the load bearing walls are normally constructed using stud walls • BS 5268: Part 6: Code of Practice for Timber Frame Walls; Section 6. 1: Dwellings not exceeding four storeys • Consist of vertical timber members, commonly referred to as studs • Studs are held in position by top and bottom plate or sole

Stud Wall Design • The most common stud sizes are 100 × 50, 47, 38 mm and 75 × 50, 47, 38 mm • The studs are usually placed at 400 or 600 mm centres • As C/C spacing is normally less than 610 mm, the load-sharing factor K 8 will apply to the design of stud walls • Frame is covered by a cladding material such as plasterboard for aesthetic reason but also provide lateral restraint to the studs about y-y axis • Horizontal noggings acts as bracing and provide lateral restraint against buckling • In addition to noggings, additional bracing may be provided if required

Stud Wall Design Load bearing stud wall

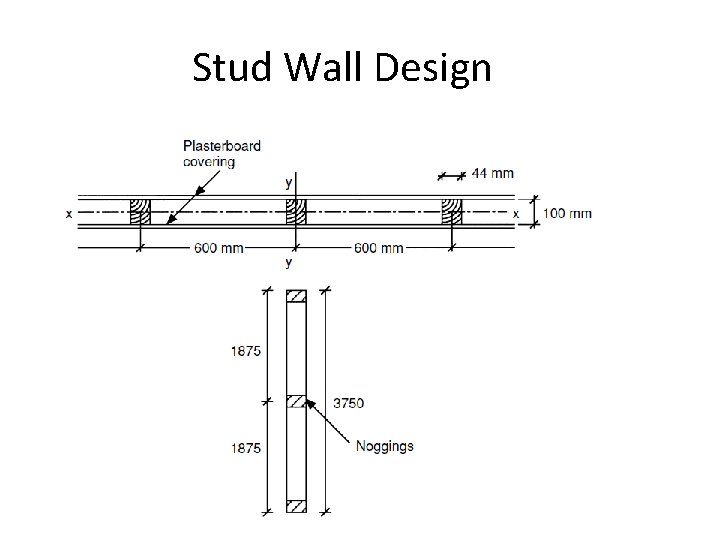
Stud Wall Design example: A stud wall panel has an overall height of 3. 75 m including top and bottom rails and vertical studs at 600 mm centres with nogging pieces at mid-height. Assuming that the studs, rail framing and nogging pieces comprise 44 × 100 mm section of strength class C 22, calculate the maximum uniformly distributed long term total load the panel is able to support.

Stud Wall Design

Stud Wall Design Effective height Lex = coefficient × L = 1. 0 × 3750 = 3750 mm Ley = coefficient × L /2 = 1. 0 × 3750/2 = 1875 mm Radius of gyration

Stud Wall Design Slenderness ratio Important: where two values of λ are possible the larger value must always be used to find σc, adm, ||

Stud Wall Design For timber of strength class C 22, Grade stress and modulus of elasticity values are (Table 8): Grade stress, σc, g, || = 7. 5 N/mm 2 & Modulus of Elasticity (Emin) = 6500 N/mm 2 Modification factors, K 2 = 1. 0 (assuming service class 1&2); K 3 = 1. 0 and K 8 = 1. 1 (due to load sharing) Emin /σc, || = Emin/(σc, g, || K 2 K 3) = 6500/(7. 5*1*1) = 866. 7 and λ = 147. 6

Stud Wall Design Table 22 (page 36) for K 12 By interpolation, K 12 = 0. 212

Stud Wall Design Permissible compressive stress: σc, adm, || = σc, g, ||* K 2* K 3*K 8*K 12 = 7. 5 × 1. 0 x 1. 0 × 1. 1 × 0. 212 = 1. 75 N/mm 2 Axial load capacity of stud: PC = σc, adm, || * Area = 1. 75 × (44 × 100) = 7. 7 k. N Hence, uniformly distributed load capacity of stud wall panel is 7. 7/0. 6 = 12. 8 KN/m

Stud Wall Design a stud wall of length 4. 2 m and height 3. 8 m, using timber of strength class C 24 to support a long term uniformly distributed load of 14 k. N/m. Solution: 1) Find applied stress (σc, a, || ) UDL = 14 KN/m Assuming that vertical studs are placed at a spacing of 600 mm C/C Therefore, total load = 14 KN/m * 0. 6 m = 8. 4 KN Assuming a stud size of 100 mm x 50 mm Therefore, applied stress = σc, a, || = 8. 4 x 103 /(100 X 50) =1. 68 N/mm 2

Stud Wall Design 2) Find permissible stress (σc, adm, || ) σc, adm, || = σc, g, ||*K 2* K 3*K 8*K 12 = 7. 9*1. 0*1. 1* K 12 Lex= 1. 0 *height = 3. 8 m = 3800 mm Ley = (½)*height = 3. 8 m/2 = 1900 mm = 28. 86 = 3800/28. 86=131. 67 = 14. 43 =1900/14. 43=131. 67

Stud Wall Design = 7200/(7. 9*1. 0) = 911. 40 K 12 from interpolation (table 22) = 0. 267 Therefore, σc, adm, || = σc, g, ||* K 3*K 8*K 12 = 7. 9 * 1. 0*1. 1* K 12 =7. 9*1. 0*1. 1*0. 267 =2. 32 N/mm 2 Since, σc, a, || (1. 68 N/mm 2) < σc, adm, || (2. 32 N/mm 2) Hence OK Note: the header spans 0. 6 m and should also be checked as a beam for given loading