Struktur und Gefgeanalyse I1 Beugungsverfahren 1 Einfhrung 2

Struktur- und Gefügeanalyse I/1 - Beugungsverfahren 1. Einführung 2. Fundamentale Entdeckungen seit 1896 3. Wellen-Teilchen-Dualität a) Photoeffekt b) Experimente von de Broglie 4. Physikalische Eigenschaften von Photonen, Elektronen und Neutronen (Energie, Wellenlänge, Ladung, …) 5. Wechselwirkung zwischen der Röntgenstrahlung, Synchrotronstrahlung, Neutronen, Elektronen und der Materie a) Bremsstrahlung, charakteristische Strahlung b) Elastische Streuung (Thomson und anomale Streuung für Photonen, Einfangquerschnitt für Neutronen) c) Nichtelastische Streuung ( – e–: Compton, Wechselwirkung n – Phonon) d) Absorption (Schwächung) und Fluoreszenz, Filter für Röntgenstrahlung e) Magnetische Wechselwirkung zwischen Neutronen und dem Werkstoff 6. Grundlagen der kinematischen Interferenztheorie a) Eindimensionale Atomkette b) Bragg-Reflexion an Netzebenen (geometrisch, analytisch) c) Ein Atom – der atomare Streufaktor d) Ein Molekül – der Formfaktor e) Ein Kristall – der Strukturfaktor f) Laue-Bedingungen, Ewald-Konstruktion g) Beispiele einfacher Strukturen (Strukturfaktoren und Auslöschen von Interferenzen) 7. Reflektion bei kleinen Winkeln 8. Das Phasenproblem 9. Verschiebung der Atome (Abweichung von der idealen Kristallstruktur) a) Statische Verschiebung der Atome b) Temperaturschwingungen der Atome (der Debye. Waller-Faktor) 10. Die wichtigsten Ergebnisse der kinematischen Interferenztheorie a) Intensität der Beugungslinien 1 b) Linienverbreiterung

Literatur 1. C. Giacovazzo: Fundamentals of Crystallography, International Union of Crystallography, Oxford Univ. Press, New York, 1992. L. V. Azároff: Elements of x-ray crystallography, Mac. Graw-Hill, New York, 1968. 3. H. P. Klug, L. E. Alexander: X-ray diffraction procedures for polycrystalline and amorphous materials, 2. edition, John Wiley & Sons, New York, 1974. A. Taylor: X-ray Metallography, John Wiley & Sons, New York, 1961. 5. Ch. Hammond: The basics of crystallography and diffraction, Oxford University Press, Oxford, 1997. 6. R. Allmann: Röntgenpulverdiffraktometrie – rechnergestützte Auswertung, Phasenanalyse und Strukturbestimmung, Loga Springer, Köln, 1994. 7. E. R. Wölfel: Theorie und Praxis der Röntgenstrukturanalyse – eine Einführung für Naturwissenschaftler, 3. , durchges. Aufl. , Vieweg, Braunschweig, 1987. 8. W. Kleber: Angewandte Gitterphysik, Walter de Gruyter & Co. , Berlin, 1941. 9. W. Kleber: Einführung in die Kristallographie, Verl. Technik, Berlin, 1998. 2

Geschichte der Röntgenbeugung und der Strukturanalyse • 1895: W. C. Röntgen – Entdeckung von Strahlen X (Nobelpreis für Physik im Jahre 1901) • 1914: Max von Laue – Entdeckung der Beugung der X-Strahlen (Röntgenstrahlung) auf Kristallen (Nobelpreis für Physik) • 1915: W. H. Bragg und W. L. Bragg – theoretische Grundlagen der Analyse der Kristallstruktur mittels Röntgenbeugung (Nobelpreis für Physik) • 1917: C. G. Barkla – Entdeckung der charakteristischen Strahlung der Elemente (Nobelpreis für Physik) • 1924: K. M. G. Siegbahn – Entdeckungen auf dem Gebiet der Spektroskopie der Röntgenstrahlung (Nobelpreis für Physik) • 1927: A. H. Compton und C. T. R. Wilson – Entdeckung und Beschreibung des „Compton-Effektes“ (Nobelpreis für Physik) • 1929: Prinz Louis-Victor Pierre Raymond de Broglie – Entdeckung der Wellennatur der Elektronen (Nobelpreis für Physik) 3

Geschichte der Röntgenbeugung und der Strukturanalyse • 1936: P. J. W. Debye – Arbeiten an der Röntgen- und Elektronenbeugung in Gasen (Nobelpreis für Chemie) • 1937: C. J. Davisson und G. P. Thomson – Experimenteller Nachweis der Elektronenbeugung an Kristallen (Nobelpreis für Physik) • 1962: J. C. Kendrew und M. F. Perutz – Struktur von Myoglobin und Hämoglobin (Nobelpreis für Chemie) • 1962: J. D. Watson, F. H. C. Crick, M. F. H. Wilkins – Bestimmung der Struktur von DNA (Nobelpreis für Chemie) • 1964: D. Crowfood-Hodkin – Bestimmung der Struktur von Penizillin, Cholesterin und Vitamin B 12 (Nobelpreis für Chemie) • 1985: J. Hauptman und J. Karle – Entwicklung der direkten Methoden für Kristallstrukturbestimmung (Nobelpreis für Chemie) • 2002: J. B. Fenn, K. Tanaka und K. Wüthrich – Entwicklung der Methoden für Identifizierung und Strukturanalyse von biologischen Makromolekülen (Nobelpreis für Chemie) 4

Physikalische Eigenschaften der Röntgenstrahlung … wurden von Wilhelm Conrad Röntgen im Jahre 1896 als folgt formuliert: • Strahlen X sind elektromagnetische Wellen, die sich im Vakuum mit der Lichtgeschwindigkeit verbreiten. Für elektromagnetische Wellen gilt (Maxwell-Gleichungen): • Vektoren des elektrischen (E) und magnetischen (H) Feldes sind zueinander orthogonal und orthogonal zur Richtung der elektromagnetischen Welle. Beide Vektoren sind eine harmonische Funktion der Zeit Spektraler Bereich der Röntgenstrahlung: • Die Wellenlänge der Röntgenstrahlung liegt zwischen der UV-Strahlung und der g. Strahlung von radioaktiven Substanzen (0, 4 – 2, 5 Å). 1 Å = 10– 10 m = 0. 1 nm. Optische Eigenschaften von Materialien: • Der Brechungsindex für Röntgenstrahlung, n» 0. 99995 • Röntgenstrahlung kann mit optischen Elementen (Linsen) nicht fokussiert werden, kann daher nicht für eine direkte Beobachtung im direkten Raum genutzt werden. Der Ausweg: Beobachtung im reziproken Raum – die Röntgenbeugung 5

Harmonische Welle E … Amplitude E 0 … max. Amplitude t … Zeit x … Position c … Lichtgeschwindigkeit … Frequenz … Kreisfrequenz … Wellenlänge k … Wellenvektor 6
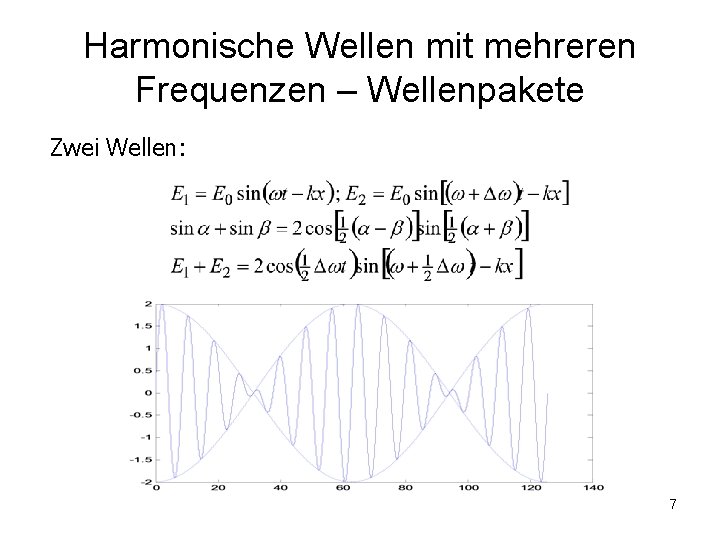
Harmonische Wellen mit mehreren Frequenzen – Wellenpakete Zwei Wellen: 7
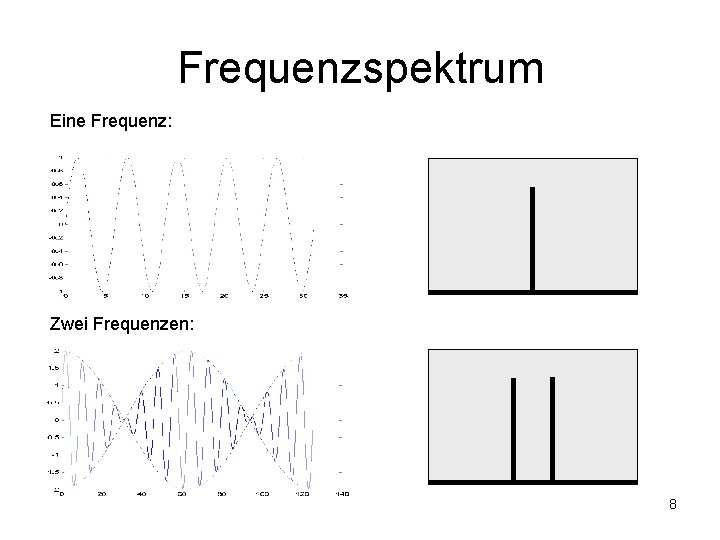
Frequenzspektrum Eine Frequenz: Zwei Frequenzen: 8
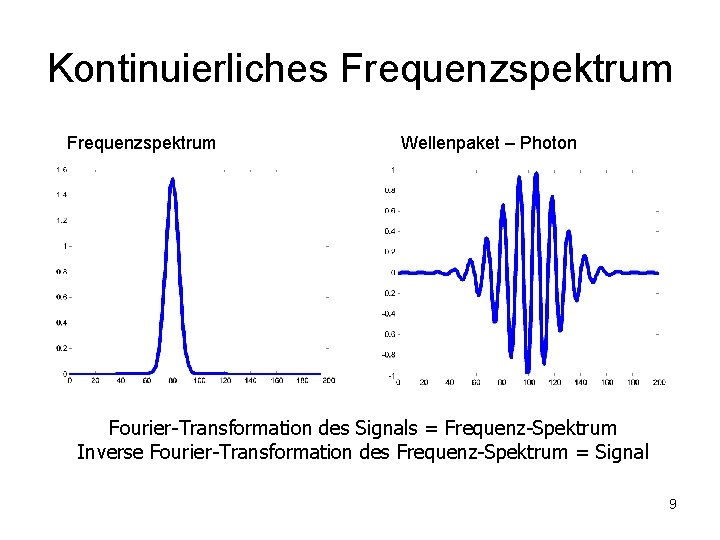
Kontinuierliches Frequenzspektrum Wellenpaket – Photon Fourier-Transformation des Signals = Frequenz-Spektrum Inverse Fourier-Transformation des Frequenz-Spektrum = Signal 9

„Länge“ des Wellenpaketes Aus dem Heisenberg-Prinzip: Die Plancksche Konstante: h = 6, 62620 x 10 -34 J. s Spektralbreite der Cu. K 1 -Strahlung: = 3. 6 x 10 -4 Å Länge des Wellenpaketes ( = 1. 54056 Å): x = 0. 66 µm 10
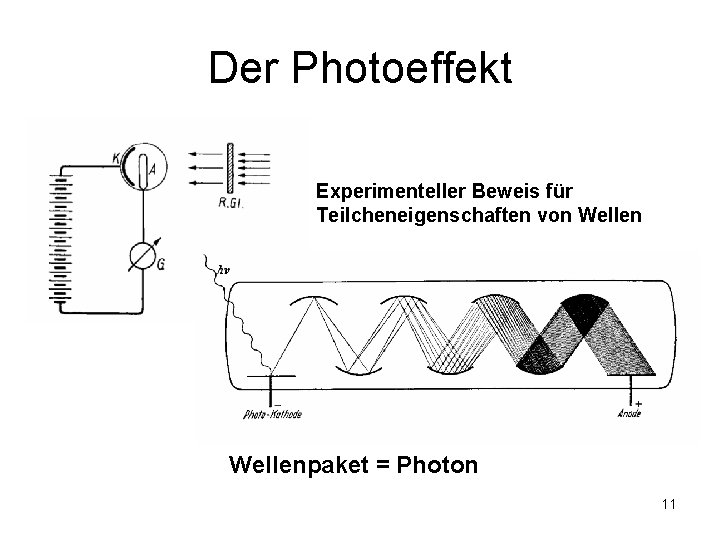
Der Photoeffekt Experimenteller Beweis für Teilcheneigenschaften von Wellenpaket = Photon 11

Welleneigenschaften von Teilchen … Energie des Photons … Impuls des Photons … Wellenlänge des Photons … de Broglie Wellenlänge eines Teilchens 12

Energie und Wellenlänge Photonen Elektronen und Neutronen 13
![Energie und Wellenlänge Photon (U in [k. V]): Elektron und Neutron (E in [e. Energie und Wellenlänge Photon (U in [k. V]): Elektron und Neutron (E in [e.](http://slidetodoc.com/presentation_image_h/d8776c1d80bc7103697682fb0c3b0ea4/image-14.jpg)
Energie und Wellenlänge Photon (U in [k. V]): Elektron und Neutron (E in [e. V]): 14
![Physikalische Eigenschaften von Photonen, Elektronen und Neutronen Eigenschaft Photon Elektron Neutron Ruhemasse [kg] 0 Physikalische Eigenschaften von Photonen, Elektronen und Neutronen Eigenschaft Photon Elektron Neutron Ruhemasse [kg] 0](http://slidetodoc.com/presentation_image_h/d8776c1d80bc7103697682fb0c3b0ea4/image-15.jpg)
Physikalische Eigenschaften von Photonen, Elektronen und Neutronen Eigenschaft Photon Elektron Neutron Ruhemasse [kg] 0 9, 11× 10 -31 1, 67× 10 -27 Ladung [C] 0 1, 60× 10 -19 0 Wellenlänge Gesamtenergie 15
- Slides: 15