Structures Matrix Analysis Introduction to Finite Element Analysis

Structures Matrix Analysis Introduction to Finite Element Analysis Sina Askarinejad 1/1 7/8/2016 1

Hook’s Law. . • 2

Application to elastic materials • 3

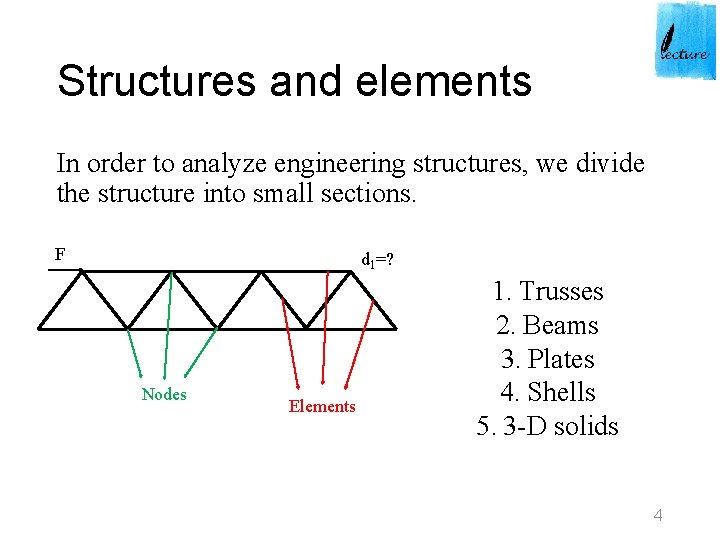
Structures and elements In order to analyze engineering structures, we divide the structure into small sections. F d 1=? Nodes Elements 1. Trusses 2. Beams 3. Plates 4. Shells 5. 3 -D solids 4

Truss • Truss is a slender member (length is much larger than the cross-section). • It is a two-force member i. e. it can only support an axial load and cannot support a bending load. • The cross-sectional dimensions and elastic properties of each member are constant along its length. • The element may interconnect in a 2 -D or 3 -D configuration in space. • The element is mechanically equivalent to a spring, since it has no stiffness against applied loads except those acting along the axis of the member. (Beam is a truss that can tolerate bending load with rotation) 5

Complex structures with simple elements 6

Finite element method • Step 1: Divide the system into bar/truss elements connected to each other through the nodes • Step 2: Describe the behavior of each bar/truss element (i. e. derive its stiffness matrix and load vector in local AND global coordinate system) • Step 3: Describe the behavior of the entire system by assembling their stiffness matrices and load vectors • Step 4: Apply appropriate boundary conditions and solve 7

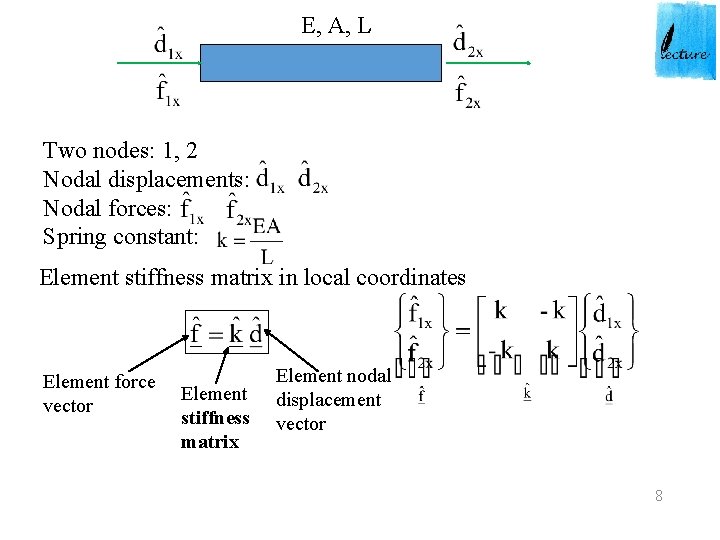
E, A, L Two nodes: 1, 2 Nodal displacements: Nodal forces: Spring constant: Element stiffness matrix in local coordinates Element force vector Element stiffness matrix Element nodal displacement vector 8

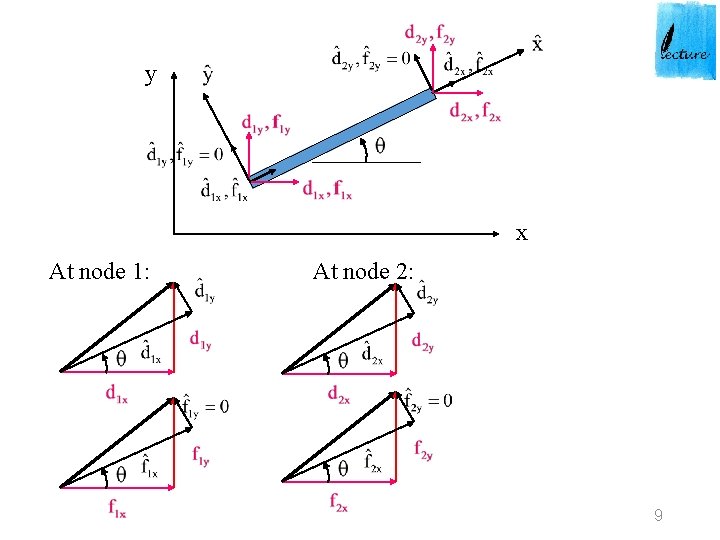
y x At node 1: At node 2: 9

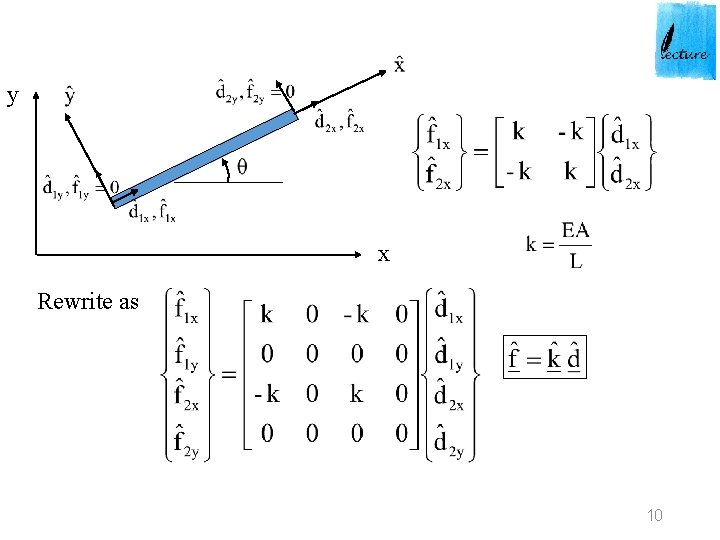
y x Rewrite as 10

In the global coordinate system, the vector of nodal displacements and loads Our objective is to obtain a relation of the form Where k is the 4 x 4 element stiffness matrix in global coordinate system 11

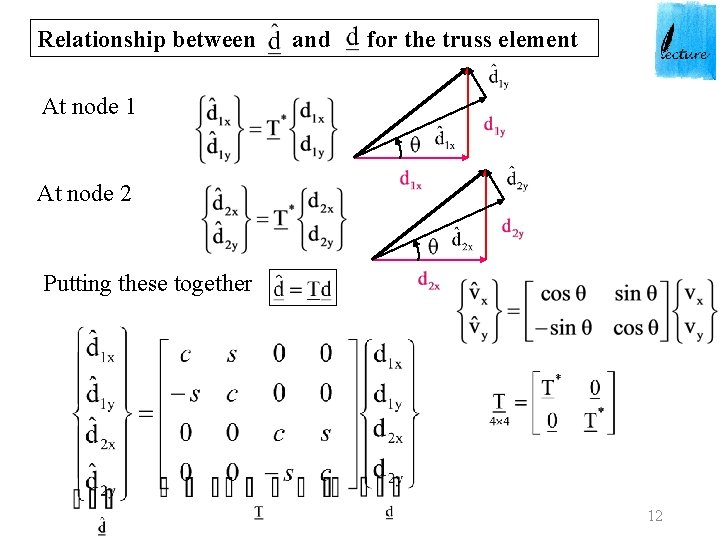
Relationship between and for the truss element At node 1 At node 2 Putting these together 12

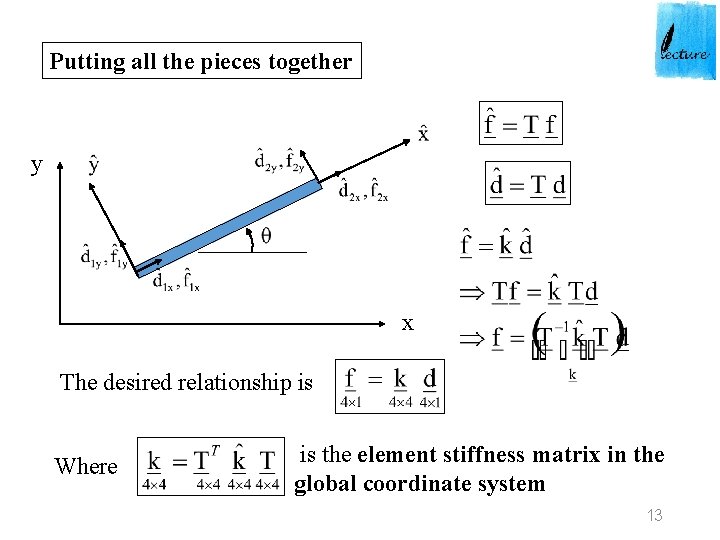
Putting all the pieces together y x The desired relationship is Where is the element stiffness matrix in the global coordinate system 13

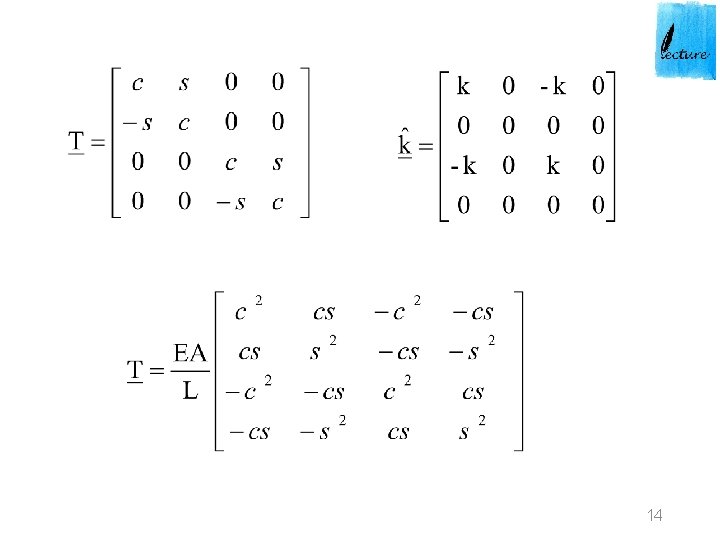
14

Assembly…. 15

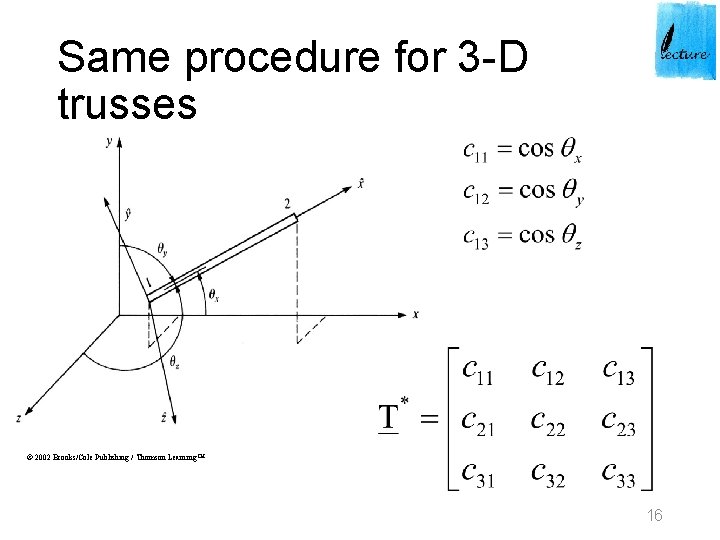
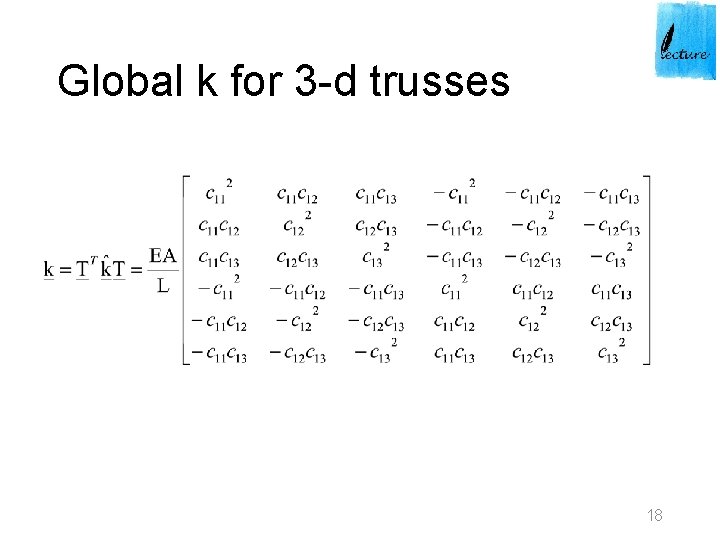
Same procedure for 3 -D trusses © 2002 Brooks/Cole Publishing / Thomson Learning™ 16

Transformation matrix T relating the local and global displacement and load vectors of the truss element Element stiffness matrix in global coordinates 17

Global k for 3 -d trusses 18

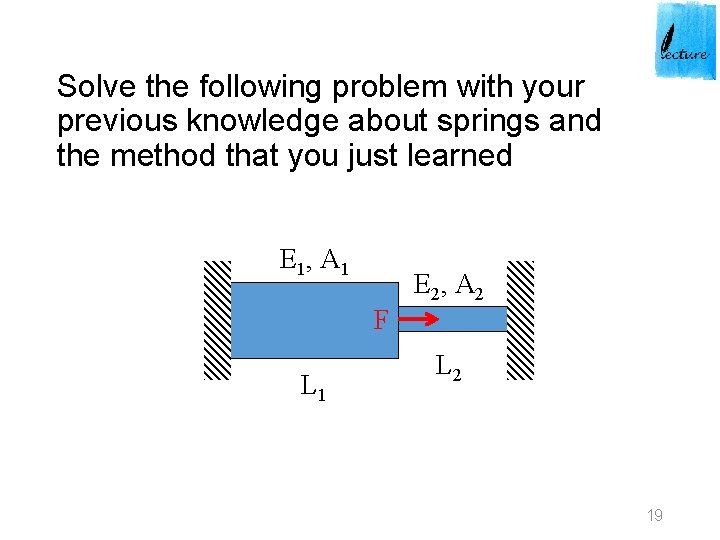
Solve the following problem with your previous knowledge about springs and the method that you just learned E 1, A 1 E 2, A 2 F L 1 L 2 19