Structured Models for MultiAgent Interactions Daphne Koller Stanford

Structured Models for Multi-Agent Interactions Daphne Koller Stanford University Joint work with David Vickrey

Nash Equilibrium n n Strategy profile : strategy for every player Regret (pi) : pi’s gain by changing strategy i Best n n = Actual Regret Nash equilibrium: s. t. each agent has 0 regret Theorem (Nash): Every game has at least one Nash equilibrium

Finding Nash Equilibria n Nash equilibria difficult to compute in games with more than 2 agents n Best current game solving package (GAMBIT): n n n 2 hrs 30 min for 6 -player 3 -action game Game representation exponential in # of agents Algorithms inherently centralized Our approach: n Structured game representation n Find approximate equilibria Fast, decentralized algorithms

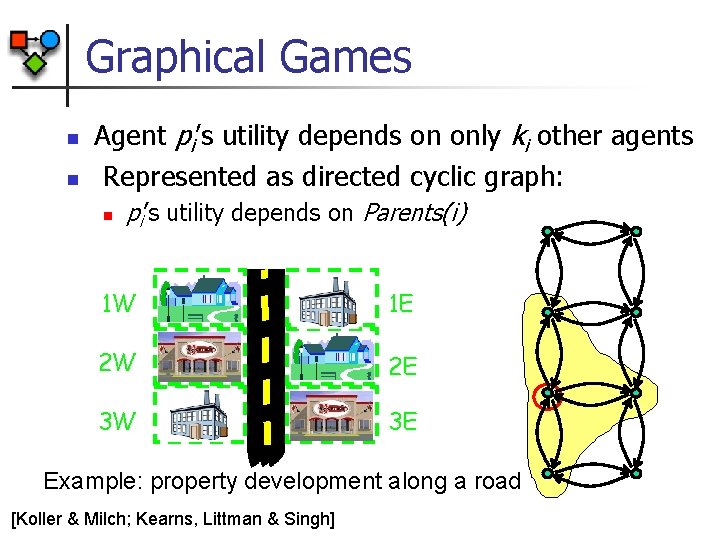
Graphical Games n n Agent pi’s utility depends on only ki other agents Represented as directed cyclic graph: n pi’s utility depends on Parents(i) 1 W 1 E 2 W 2 E 3 W 3 E Example: property development along a road [Koller & Milch; Kearns, Littman & Singh]

Approximate Equilibria -optimal Nash equilibrium: each agent’s regret

Constraint Satisfaction n n Constraint: each agent has zero regret Constraints are local since regret is local n Each involves only node and its parents

Solving the CSP n Problem: Strategies are continuous Solution: n n n Discretize strategy space of each player Constraint: regret of agent in table Produces -approximate equilibria n The finer the discretization, the lower the S’s strategy S 2 actions T T’s strategy n 0 0. 33. 66 1 . 2. 4. 6. 8 1

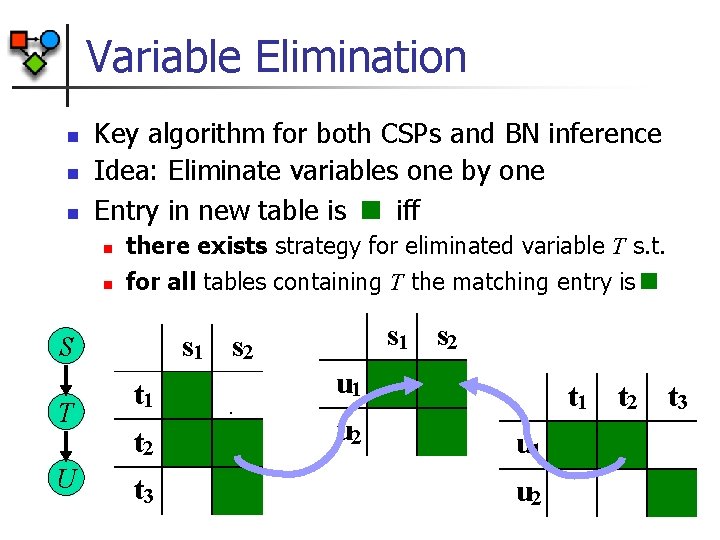
Variable Elimination n Key algorithm for both CSPs and BN inference Idea: Eliminate variables one by one Entry in new table is iff n n there exists strategy for eliminated variable T s. t. for all tables containing T the matching entry is T U s 1 s 2 S t 1 t 2 t 3 u 1 u 2

Cost Minimization n Problem: Discretization too sparse no -equilibrium Solution: replace in constraint tables with regrets To eliminate T: n n n entry in new table is min over all strategies of T of max over all tables Finds best -equilibrium for given discretization S s 1 s 2 T t 1. 3. 1 t 2. 5. 2 t 3 0. 3 u 1 0. 2 u 2. 3. 1 U t 1 t 2 t 3 u 1. 4. 2 0 u 2. 1. 6. 3

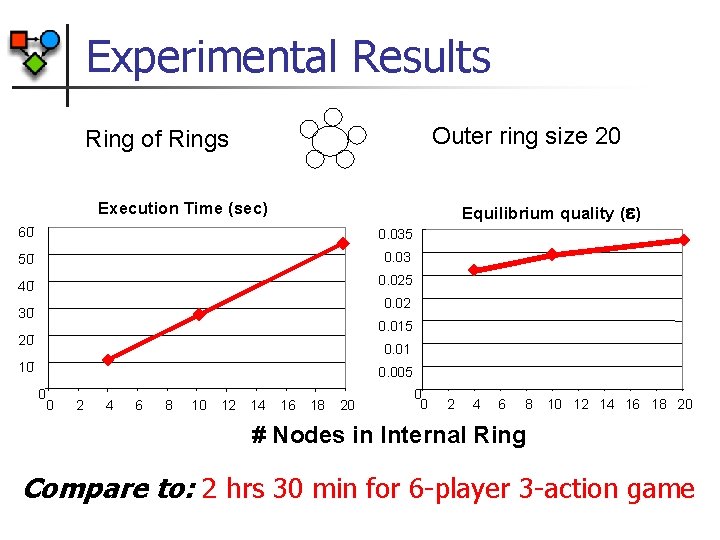
Experimental Results Outer ring size 20 Ring of Rings Equilibrium quality ( ) Execution Time (sec) 60 0. 035 50 0. 03 40 0. 025 0. 02 30 0. 015 20 0. 01 10 0. 005 0 0 2 4 6 8 10 12 14 16 18 20 # Nodes in Internal Ring Compare to: 2 hrs 30 min for 6 -player 3 -action game

Conclusion n Finding equilibria is hard: n n Computationally complex Requires centralized solution Used graphical language, similar to BNs, to represent structure Adapted graphical algorithm to find equilibria n n Significantly more efficiently In a decentralized way